Уравнение майера физический смысл универсальной газовой постоянной (6 видео)

Содержание

Формула Майера для теплоемкостей идеального газа, пример задачи
Идеальный газ и его уравнение
Внутренняя энергия и изохорный процесс
Формула Майера для теплоемкостей
Задача на определение теплоемкостей воздуха
Уравнение майера физический смысл универсальной газовой постоянной
Уравнение Майера
Теплоемкость. Уравнение Майера
Уравнение Майера для идеального газа
🔥 Видео

Видео:Универсальная молярная газовая постоянная. Уравнение Менделеева - Клапейрона 10 классСкачать

Формула Майера для теплоемкостей идеального газа, пример задачи

Многие газы в физике принято описывать в рамках идеальной модели, с помощью которой можно легко определить основные термодинамические характеристики системы. В данной статье приведем вывод формулы Майера для газа идеального и покажем, как ее можно использовать для решения задачи.

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Идеальный газ и его уравнение

Чтобы понять вывод формулы Майера, следует ближе познакомиться с моделью идеального газа. Согласно ей, термодинамическая система представляет собой совокупность частиц, которые не обладают размерами (являются материальными точками). Их кинетическая энергия является единственной компонентой внутренней энергии системы (потенциальная энергия взаимодействий равна нулю), и скорости частиц подчиняются классическому распределению Максвелла-Больцмана.

Описанная модель хорошо подходит для многих реальных газообразных систем, состоящих из химически инертных атомов и молекул, и имеющих невысокие давления и температуры в несколько сотен кельвин.

Идеальный газ описывается универсальным выражением, которое называется законом Клапейрона-Менделеева. Оно приведено ниже:

Здесь P, V, T — три термодинамических величины: давление, объем и температура. Параметры n и R — это количество вещества в системе и постоянная для всех газов, соответственно.

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Внутренняя энергия и изохорный процесс

Согласно определению, внутренняя энергия U произвольной системы равна сумме потенциальной и кинетической энергий ее элементов. Выше отмечалось, что в идеальной модели газовые молекулы и атомы друг с другом не взаимодействуют, это означает, что внутренняя энергия определяется исключительно кинетической составляющей.

Из кинетической теории газов следует равенство, связывающее среднюю кинетическую энергию частицы с абсолютной температурой в системе:

Где m — масса одной частицы, k_B — Больцмана константа, v — скорость средняя квадратичная, z — число степеней свободы. Если обе части равенства умножить на количество N частиц в системе, то мы получим выражение для внутренней энергии U:

При записи этого выражения мы воспользовались следующими равенствами:

Теперь рассмотрим вопрос определения внутренней энергии газа с точки зрения термодинамики. Обратимся к изохорному процессу. В результате него все подводимое тепло идет на нагрев системы, поскольку объем остается постоянный, и работа газа равна нулю, то есть:

В свою очередь, изменение величины U можно записать так:

Где C_V — теплоемкость системы при постоянном объеме. Эта величина показывает, сколько энергии в джоулях необходимо затратить, чтобы нагреть систему на 1 Кельвин. Сравнивая это выражение с формулой для U, которая получена из кинетической теории, приходим к равенству:

Вместо теплоемкости C_V часто пользуются молярной изохорной теплоемкостью, то есть той же величиной, только для 1 моля газа:

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Формула Майера для теплоемкостей

Чтобы получить названную формулу, следует рассмотреть с точки зрения термодинамики изобарный процесс. Под ним понимают переход системы между двумя равновесными состояниями, при котором давление не изменяется. Предположим, что в рассматриваемой системе содержится 1 моль газа, тогда первое начало термодинамики для изобарного процесса примет вид:

Теперь введем понятие об изобарной теплоемкости C_P. Под ней понимают количество теплоты, которое следует системе сообщить, чтобы она нагрелась на 1 Кельвин, а ее давление при этом не изменилось. Это определение позволяет переписать равенство выше в виде:

Если вспомнить уравнение для 1 моля идеального газа и выражение для изменения внутренней энергии, то это равенство запишется так:

Это выражение называется формулой Майера для идеального газа. Оно показывает, что изобарная теплоемкость всегда больше изохорной на величину газовой постоянной для 1 моля газа. Значение же газовой постоянной R также приобретает конкретный физический смысл — это работа, которую совершает один моль газа во время его изобарного расширения при нагреве на один Кельвин.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Задача на определение теплоемкостей воздуха

Необходимо вычислить молярные теплоемкости C_P и C_V для воздуха, полагая его идеальным газом.

Решить эту задачу несложно, если вспомнить, что изохорная молярная теплоемкость равна:

Тогда в соответствии с формулой Майера молярная величина C_P будет равна:

Поскольку воздух на 99% образован двухатомными молекулами O₂ и N₂, то z для него равно 5. Подставляя это значение, а также значение R=8,314 Дж/(К*моль) в формулы, получаем ответы на задачу: C_V = 20,8 Дж/(К*моль), C_P = 29,1 Дж/(К*моль).

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Уравнение майера физический смысл универсальной газовой постоянной

Теплоёмкость идеального газа. Уравнение Майера

Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:

(4.2.1)

Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.

Удельная теплоёмкость (С_уд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [C_уд] = Дж/К.

Для газов удобно пользоваться молярной теплоемкостью Cμ— количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:

(4.2.2)

Из п. 1.2 известно, что молярная масса – масса одного моля:

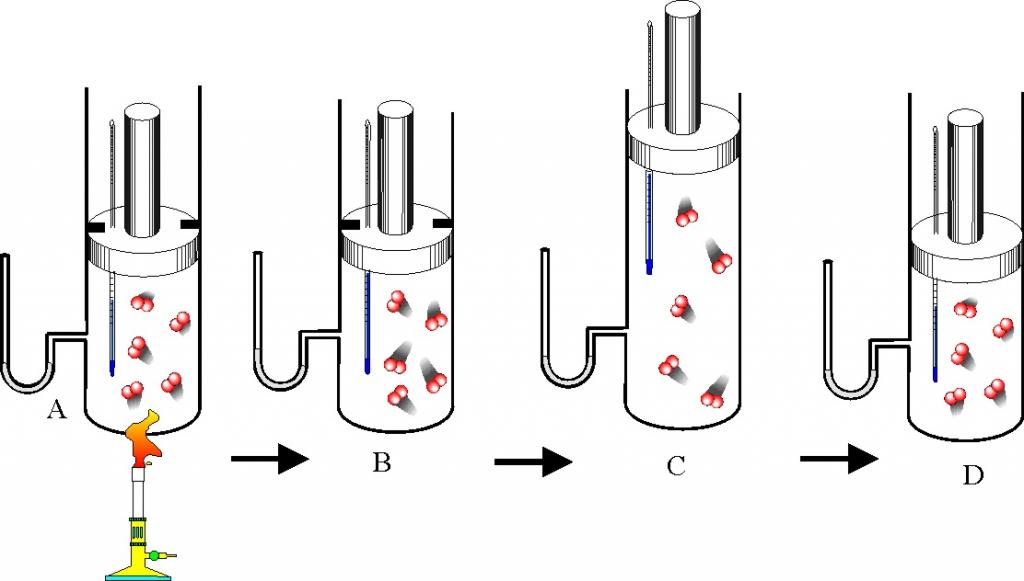
Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.

Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается С_V.

С_Р – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2).

Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния.

Величины С_Р и С_V оказываются связанными простыми соотношениями. Найдём их.

Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:

(4.2.3)

Теплоемкость при постоянном объёме будет равна:

(4.2.4)

Из (4.2.4) следует, что

(4.2.5)

Для произвольной идеальной массы газа:

(4.2.6)

При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:

(4.2.7)

(4.2.8)

Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.

Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.

Полезно знать формулу Майера для удельных теплоёмкостей:

Видео:Термодинамика | уравнение МайераСкачать

Уравнение Майера

Уравнение Майера связывает теплоемкости идеального газа в двух изопроцессах, тогда перейдем к самому его определению.

Видео:Адиабатный процесс. 10 класс.Скачать

Теплоемкость. Уравнение Майера

Переданное телу количество теплоты для его нагревания на 1 К получило название теплоемкости тела данной системы. Обозначение принимается буквой » С » :

Значение теплоемкости единицы молярной массы тела:

c μ = C v ( 2 ) . Выражение называется молярной теплоемкостью.

Теплоемкость не считается функцией состояния, так как является характеристикой бесконечно близких состояний системы или выражается в качестве функции бесконечно малого процесса, совершаемого в системе. В количественном выражении это означает, что из ( 1 ) , применяя первое начало термодинамики, дифференциальная форма получится:

C = δ Q d T = d U + p d V d T ( 3 ) .

Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение Майера для идеального газа

Определение термодинамической системы производится при помощи трех параметров p , V , T . Существующее между ними отношение получило название уравнения состояния. Для идеального газа используется уравнение Менделеева-Клапейрона. Данная связь запишется в виде:

p = p ( T , V ) или T = T ( p , V ) , V = V ( p , T ) .

При выборе независимых переменных в качестве V и T внутренняя энергия системы выражается в виде функции U = U ( T , V ) . Получим, что значение полного дифференциала от внутренней энергии примет вид:

d U = ∂ U ∂ T V d T + ∂ U ∂ V T d V ( 4 ) .

Произведем подстановку из ( 4 ) в ( 3 ) , тогда

c = ∂ U ∂ T V d T + ∂ U ∂ V T d V + p d V d T = ∂ U ∂ T V + p + ∂ U ∂ V T d V d T ( 5 ) .

Исходя из формулы ( 5 ) , теплоемкость находится в зависимости от процесса. Если он изохорный, то

Значение теплоемкости изохорного процесса запишется как:

C V = ∂ U ∂ T V ( 6 ) .

При изобарном теплоемкость выражается через формулу:

C p = ∂ U ∂ T V + p + ∂ U ∂ V T ∂ V ∂ T p = C V + p + ∂ U ∂ V T ∂ V ∂ T p ( 7 ) .

Перейдем к рассмотрению исследуемой системе идеального газа. Запись малого приращения энергии идеального газа:

d U = i 2 v R d T ( 8 ) .

d U d V T = 0 ( 9 ) .

Состояние идеального газа описывается при помощи уравнения Менделеева-Клапейрона:

∂ V ∂ T p = v R p ( 11 ) .

Произведем подстановку в ( 7 ) из ( 10 ) и ( 11 ) :

C p = C V + p + 0 v R p = C V + v R ( 12 ) .

Выражение ( 12 ) называют выведенным соотношением Майера.

Или для молярных теплоемкостей:

C μ p = C μ V + R ( 13 ) .

Найти удельную теплоемкость смеси 16 г кислорода и 10 г гелия в процессе с постоянным давлением.

Если Q считается количеством тепла, получаемым смесью газов в процессе, то

Q = c p m ∆ T ( 1 . 1 ) , где m является массой смеси, c p – удельной теплоемкостью смеси при неизменном давлении.

Q O 2 — это количество тепла, получаемое кислородом:

Q O 2 = c p O 2 m O 2 ∆ T ( 1 . 2 ) , m O 2 выражается массой кислорода, c p O 2 – теплоемкостью кислорода с постоянным давлением.

Для гелия аналогично:

Q H e = c p H e m H e ∆ T ( 1 . 3 ) .

Кроме этого рассмотрим:

Q = c p m ∆ T = Q O 2 + Q H e = c p O 2 m O 2 ∆ T + c p H e m H e ∆ T ( 1 . 4 ) .

Нахождение массы смеси производится по закону сохранения массы:

m = m O 2 + m H e ( 1 . 5 ) .

Произведем выражение теплоемкости c p из ( 1 . 4 ) , учитывая ( 1 . 5 ) . Тогда имеем:

c p = c p O 2 m O 2 + c p H e m H e m O 2 + m H e ( 1 . 6 ) .

Существует связь между молярной теплоемкостью и удельной:

c μ = c · μ → c = c μ μ ( 1 . 7 ) .

Если c μ V = i 2 R , то по уравнению Роберта Майера c μ p = c μ V + R :

c μ p = i + 2 2 R ( 1 . 8 ) ; i H e = 3 , i O 2 = 5 .

В данном случае удельные теплоемкости запишутся как:

c p H e = 5 2 R μ H e , c p O 2 = 7 R 2 μ O 2 ( 1 . 9 ) .

Результатом будет записанная формула удельной теплоемкости смеси:

c p = 7 R 2 μ O 2 m O 2 + 5 2 R μ H e m H e m O 2 + m H e ( 1 . 10 ) .

c p = 3 , 5 · 8 , 31 · 16 32 + 2 , 5 · 8 , 31 · 10 4 26 = 14 , 5 + 51 , 94 26 = 2 , 56 Д ж г К .

Ответ: удельная теплоемкость смеси равняется 2 , 56 Д ж г К .

При проведении опытов Джоулем было получено, что с μ p — c μ V = 1 , 986 к а л К · м о л ь . Значение газовой постоянной, измеренной в механических единицах R = 8 , 314 · 10 7 э р г К · м о л ь . Определите, как соотносятся 1 к а л , э р г , Д ж .

Основой решения данного задания принято считать уравнение Майера, формула записывается:

с μ p = c μ V + R → c μ p — c μ V = R ( 2 . 1 ) .

Отсюда получим, что:

c μ p — c μ V = 1 , 986 к а л К · м о л ь = 8 , 314 · 10 7 э р г К · м о л ь → 1 к а л = 4 , 18 · 10 7 э р г = 4 , 18 Д ж .

Ответ: 1 к а л = 4 , 18 · 10 7 э р г = 4 , 18 Д ж .