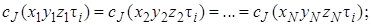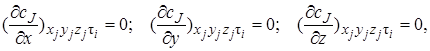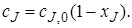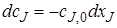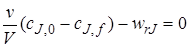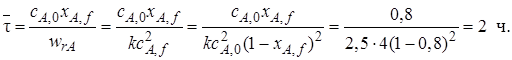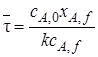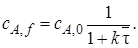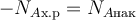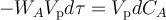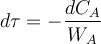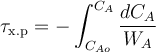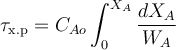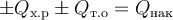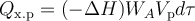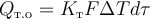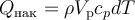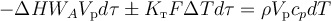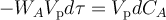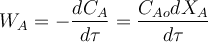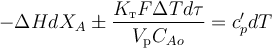Уравнение материального баланса для реактора идеального смешения (4 видео)

Содержание

Реактор идеального смешения
Материальный баланс РИС-П
Уравнение материального баланса для реактора идеального смешения
📹 Видео

Видео:Модели реакторов идеального вытеснения и идеального смешенияСкачать

Реактор идеального смешения

Для модели идеального смешения принимается ряд допущений. Допускается, что в результате интенсивного перемешивания устанавливаются абсолютно одинаковые условия в любой точке реактора: концентрации реагентов и продуктов, степени превращения реагентов, температура, скорость химической реакции и т. д. Например, в некоторый момент времени τ_j во всех точках ректора (рис. 5.1) выполняются следующие условия:

где x, у, z – пространственные координаты.

В проточном реакторе идеального смешения концентрации элементов реакции в выходном потоке в рассматриваемый момент времени τ_i строго равны концентрациям тех же веществ в реакторе.

Чтобы перечисленные допущения могли быть выполнены, необходимо принять еще одно допущение: переход от одной концентрации к другой в реакторе идеального смешения не должен иметь протяженности во времени. Изменение концентрации исходного реагента от начальной c_J_,₀ во входном потоке в данный момент времени τ_i до концентрации в реакторе с_J в этот же момент времени должно происходить мгновенно (скачкообразно).

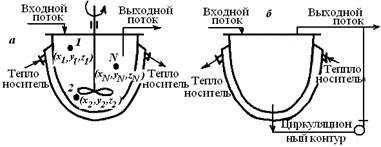
Приблизиться к режиму идеального смешения можно, обеспечив интенсивное перемешивание реакционной смеси механическими мешалками разного типа или циркуляционными насосами, создающими высокую кратность циркуляции. Смешение, близкое к идеальному смешению, легче выполнить в емкостных аппаратах с приблизительно равным диаметром и высотой.

Так как в реакторе идеального смешения концентрации элементов реакции равномерно распределены по объему, то уравнение материального баланса (4.7), выведенное для элементарного объема, можно распространить на полный объем реактора.

Рассмотрим два частных случая: периодический реактор идеального смешения и проточный реактор идеального смешения, работающий в стационарном режиме.

Периодический реактор идеального смешения.В периодический реактор все реагенты вводят до начала реакции, а все продукты выводят из него только по окончании процесса. В ходе реакционного цикла никаких веществ в реактор не вводят и из него не выводят, так что общая масса реакционной смеси в реакторе остается постоянной, изменяется лишь ее состав. При составлении математического описания принимают, что реакционная смесь однородна по объему аппарата и ее состав зависит только от времени пребывания в периодическом реакторе.

Рис. 5.1. Схемы реакторов идеального смешения
с механическим перемешивающим устройством (а)
и циркуляционным контуром (б)

Из общего уравнения материального баланса (4.7) в случае периодического реактора идеального смешения можно исключить два первых оператора, описывающих явления конвективного и диффузионного переноса вещества в аппарате. При отсутствии перемещения потока через реактор в произвольный момент времени между началом и окончанием процесса средняя линейная скорость элемента потока равна нулю, следовательно, и конвективный перенос в непроточном реакторе отсутствует. Заключение об отсутствии диффузионного переноса вытекает из допущений модели идеального смешения, так как диффузия возможна лишь при наличии градиента концентраций, а при равномерном распределении концентраций по объему он равен нулю. (Этот вывод справедлив не только для периодического, но и для проточного реактора идеального смешения.)

Следовательно, уравнение материального баланса для периодического реактора идеального смешения примет вид

(5.1)

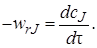
В уравнении (5.1) частная производная заменена на полную, так как в соответствии с допущениями идеального смешения концентрация с внутри реактора является функцией только одной переменной – времени.

Уравнение материального баланса периодического реактора идеального смешения (5.1) совпадает с уравнением (3.2), дающим определение скорости химического превращения. Из одинакового вида уравнений косвенно можно сделать вывод, что гидродинамическая обстановка в периодическом реакторе идеального смешения не накладывает ограничений на химическую кинетику.

Для проведения расчетов по уравнению (5.1) в его левую часть вместо w_rJ(c_J)вводят конкретное кинетическое уравнение. Тогда можно рассчитать, например, время реакционного цикла, необходимое для достижения заданной глубины превращения (заданной конечной концентрации с_J_,f):

(5.2)

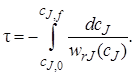
Если вещество J – исходный реагент, то концентрацию c_s можно выразить через его степень превращения:

и уравнение (5.2) примет вид

(5.3)

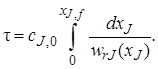
Уравнения (5.2) и (5.3) позволяют также рассчитать зависимость концентрации реагента с_J или его степени превращения х_J от времени пребывания в реакторе (продолжительности реакционного цикла). В разные моменты времени условия в периодическом реакторе различные (концентрация реагентов, продуктов, скорость реакции и т. д.), однако в каждый данный момент времени из-за допущения об идеальности эти параметры строго одинаковы в объеме реактора (рис. 5.2).

Время, рассчитанное по уравнению (5.2) или (5.3), является «чистым» временем, необходимым для проведения химического превращения. Однако для осуществления процесса в периодическом реакторе кроме этого «реакционного» времени нужно затратить вспомогательное время на загрузку реагентов, выведение реактора на нужный технологический режим, разгрузку и очистку. Полное время одного цикла работы периодического реактора суммируется из основного τ_хр и вспомогательного τ_всп.

Рис. 5.2. Изменение концентрации исходного реагента
в периодическом реакторе идеального смешения во времени (а)
и по объему аппарата (б)

Наличие τ_всп как составной части времени цикла приводит к снижению производительности химического реактора (количество продукта, получаемого в единицу времени) и является одним из существенных недостатков периодических процессов вообще. Другие их недостатки – большие затраты ручного труда, сложность решения задач автоматизации (так как условия в реакторе во времени постоянно меняются).

Однако периодические реакторы обычно можно приспособить к широкому диапазону условий реакций, что удобно при необходимости производить на одной установке различные химические продукты, например, в промышленности химических реактивов.

Периодические реакторы с интенсивным перемешиванием, приближающимся к идеальному смешению, применяют в производствах реактивов, органических красителей, лекарственных препаратов – там, где для достижения достаточной глубины превращения требуется сравнительно длительное время, а объемы производства невелики.

Периодические реакторы смешения часто применяют в микробиологической промышленности для культивирования аэробных микроорганизмов. Процесс культивирования для большинства микроорганизмов длится 48–72 ч, т. е. достаточно длителен. Интенсивное перемешивание в ферментаторе позволяет обеспечить равномерное распределение температуры, что особенно важно в таких процессах, так как даже небольшие локальные разогревы могут привести к гибели микроорганизмов. Изолированность реакционной системы в периодическом реакторе позволяет устранить опасность отравления микроорганизмов случайными примесями, которые могут попасть в аппарат при непрерывной подаче реагентов.

Окончательное решение о целесообразности применения периодического или непрерывного процесса можно вынести лишь на основании экономической оценки (сравнения расходов на эксплуатацию, амортизацию, электроэнергию, пар, сырье и т. д.). Как правило, при проведении такого сравнения оказывается, что периодические процессы выгодны при относительно невысокой производственной мощности в тех случаях, когда получают дорогостоящие продукты.

Проточный реактор идеального смешения в стационарном режиме.Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывно действующих реакторах с установившимся режимом. Распространенным видом таких проточных аппаратов являются реакторы смешения. Проточный реактор смешения может работать как в нестационарном режиме (пуск, выход на режим, остановка), так и в стационарном, установившемся режиме.

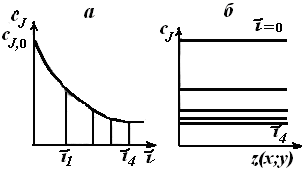
Рассмотрим уравнение материального баланса для стационарного проточного реактора идеального смешения без циркуляции. Получим его, опять упрощая общее уравнение материального баланса (4.7). Для любого реактора идеального смешения, и в частности для проточного, из уравнения можно исключить оператор, описывающий диффузионный перенос. При стационарном режиме работы реактора из уравнения исключается производная дс_J/дτ,не равная нулю только при наличии накопления вещества в реакторе.

Таким образом, в уравнении остаются только два члена, описывающие конвективный перенос вещества J и расход или образование этого вещества в ходе химической реакции.

Оператор конвективного переноса (переноса импульса), записанный в уравнении (4.7) в дифференциальной форме, можно представить для проточного реактора идеального смешения в конечно-разностной форме. В соответствии с допущениями модели идеального смешения в проточном реакторе происходит дискретное конечное (а не бесконечно малое) изменение концентрации ∆с_J сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации ∆с_J к изменению координаты ∆z при прохождении реакционного потока через реактор со средней линейной скоростью 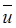. 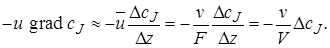Среднюю линейную скорость потока можно заменить через отношение объемного расхода v через реактор к площади поперечного сечения F. Тогда, с учетом того, что произведение F∆z равно объему реактора V,член уравнения, описывающий конвективный перенос, примет вид

(5.4)

В выражении (5.4) ∆с_J равно разности концентраций на выходе из реактора c_if и на входе в реактор с_J_,0. Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так:

. (5.5)

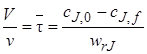
Это же уравнение можно получить и другим путем. Как указывалось, в качестве элементарного объема для реактора идеального смешения можно принять полный объем реактора V. При стационарном режиме работы реактора не происходит изменения постоянных по объему концентраций элементов реакции и во времени, следовательно, в качестве элементарного промежутка времени можно принять любой конечный временной интервал, например единицу времени (1 с, 1 мин или 1 ч).

Количество вещества J, которое за единицу времени войдет в реактор с конвективным потоком, будет равно v₀c_J_,0,где v₀ – объемный расход реакционного потока на входе в аппарат. За это же время выйдет из реактора с конвективным потоком количество вещества J = v_fc_J_,f,а расход вещества J (или его образование) в ходе химической реакции составит w_rJ V. При этом скорость w_rJ определяется концентрацией c_J_,f.

Стационарность процесса в проточном реакторе можно обеспечить, если объемные расходы на входе v₀ и выходе v_f равны между собой
(v₀ = v_f = v).

. (5.6)

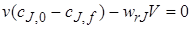
Очевидно, что уравнение (5.6) тождественно уравнению (5.5).

Величина = V/v в уравнении (5.5) измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержимое проточного реактора. Эту величину называют средним временем пребывания реагентов в проточном реакторе.

Действительное время пребывания частиц в проточном реакторе смешения является случайной величиной в отличие от времени пребывания реагентов в периодическом реакторе. Пусть, например, в реактор введено N одинаковых частиц. В периодическом реакторе все они будут находиться равное время от загрузки до выгрузки. В проточном реакторе идеального смешения эти частицы мгновенно и равномерно распределяются по всему объему аппарата, и так как из аппарата непрерывно выходит поток продуктов, то в момент ввода частиц в реактор какое-то их количество может сразу же оказаться в выходном потоке. Некоторые частицы, равномерно распределяясь в новых порциях реакционной смеси, вошедшей в аппарат, могут находиться в нем бесконечно долго. Отсюда можно сделать вывод, что действительное время пребывания частиц в проточном реакторе – это случайная величина, которая может изменяться от 0 до ∞. Непрерывную случайную величину можно задать с помощью вероятностных характеристик, в частности функций распределения случайной величины. Использование в качестве характеристики времени пребывания частиц в проточном реакторе величины является удобным способом усреднения действительного времени пребывания, так как эта величина связана с конструктивными характеристиками реактора: его объемом и объемным расходом реакционной смеси.

Для решения практических задач удобно концентрацию реагента c_J_,fвыразить через его степень превращения х_J_,f:

. (5.7)

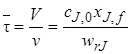
Уравнения материального баланса (5.5)–(5.7) для проточного реактора идеального смешения в стационарном режиме имеют ряд отличий от соответствующих уравнений для периодического реактора (5.2) и (5.3). Следует отметить, что балансовые уравнения стационарного реактора идеального смешения записываются сразу в виде конечного алгебраического уравнения в отличие от дифференциальной формы исходных уравнений для периодического реактора.

В уравнение для периодического реактора скорость w_r_,Jследует подставлять в виде функциональной зависимости от концентрации w_r_,_J(c_j) или степени превращения w_r_,_J(x_j) и лишь после интегрирования уравнения возможна подстановка числовых значений. Этот факт, как и дифференциальная форма уравнений материального баланса, отражает зависимость параметров процесса в периодическом реакторе от времени. В стационарном режиме в любой точке реактора идеального смешения в любой момент времени концентрация постоянна. Следовательно, скорость реакции характеризуется каким-то одним конкретным числовым значением, определяемым этой концентрацией. Это число может быть сразу поставлено в уравнение материального баланса.

Пример 5.1.Рассчитать среднее время пребывания реагентов в проточном реакторе идеального смешения, необходимое для достижения степени превращения исходного реагента х_А_,f= 0,8.

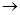
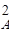
В реакторе протекает реакция второго порядка 2А R + S, скорость которой описывается при постоянной температуре кинетическим уравнением w_rA = 2,5 . Начальная концентрация реагента А на входе в реактор с_А_,₀ = 4 кмоль/м 3 .

Решение. Для определения можно использовать уравнение (5.7); концентрацию реагента в реакторе, необходимую для расчета скорости протекающей в нем реакции, выразим через степень превращения

Таким образом, для достижения степени превращения х_А = 0,8 необходимо, чтобы соотношение между объемом реактора и объемным расходом через него = V/v = 2 ч.

Уравнения материального баланса для проточного реактора могут быть использованы не только для определения среднего времени пребывания и затем размеров реакционного пространства (V = v )при заданной глубине химического превращения, но и для решения обратной задачи: при заданных объеме реактора и производительности по исходному реагенту (пропорциональной объемному расходу v)определить концентрацию реагентов на выходе из реактора.

Решение этой задачи не вызывает никаких затруднений, если скорость реакции описывается сравнительно простыми кинетическими уравнениями (уравнениями первого и второго порядка). Например, для реакции первого порядка А 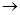R из уравнения материального баланса (5.5)

Зачастую скорость сложных реакций с невыясненным до конца механизмом выражают в виде кинетических уравнений дробного порядка. В этом случае аналитическое решение оказывается невозможным и приходится прибегать к численным методам расчета. В качестве примера рассмотрим весьма наглядный графический метод определения концентрации реагентов на выходе из стационарного проточного реактора идеального смешения.

Запишем уравнение материального баланса (5.5) в следующем виде:

. (5.8)

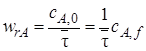
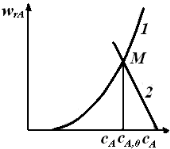
Уравнение (5.8) представляет собой равенство двух разных функций от концентрации. В левой части уравнения записана функция w_rА(с_А), представляющая собой кинетическое уравнение реакции. В соответствии с законом действующих масс скорость химических реакций пропорциональна концентрациям реагентов, следовательно, w_rA(c_A) – это возрастающая функция, которую легко представить графически (рис. 5.3, линия 1). Она пересекает ось абсцисс в точке, соответствующей равновесной концентрации с_А_,_е для обратимых реакций, или исходит из начала координат в случае необратимых реакций.

Рис. 5.3. Зависимость скорости реакции от концентрации реагента
на выходе из проточного реактора идеального смешения,
используемая для определения конечной концентрации

В правой части уравнения (5.8) записана соответствующая уравнению материального баланса стационарного реактора идеального смешения линейная функциональная зависимость скорости реакции от концентрации исходного реагента, имеющая отрицательный угловой коэффициент (–1/ ). График этой зависимости – прямая линия, пересекающая ось абсцисс (ось концентраций) в точке с_А= с_А_,₀ (линия 2).

Уравнению (5.8) удовлетворяют такие значения концентраций с_А, при которых значения функций, стоящих в левой и правой частях этого уравнения, равны. Иначе – такие концентрации, при которых графики этих функций пересекаются. Как видно, линии 1 и 2 пересекаются в единственной точке М.Абсцисса этой точки и есть искомая концентрация реагента на выходе из реактора идеального смешения.

Дата добавления: 2015-06-17 ; просмотров: 7969 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Химические реакторыСкачать

Материальный баланс РИС-П

Описание модели РИС-П

Реактор идеального смешения периодического действия представляет собой ёмкостный аппарат с перемешивающим устройством.
В периодический реактор все реагенты помещают до начала реакции, а продукты извлекают из него только после проведения процесса.
Общая масса реакционной смеси в реакторе остается постоянной, а изменяется лишь ее состав.
Условием идеальности работы реактора смешения периодического действия является мгновенное установление одинаковых параметров процесса в реакционном объеме аппарата в результате интенсивного перемешивания.

Уравнение материального баланса для реактора идеального смешения

Схема реактора идеального смешения периодического действия:

1 – внутренний объем реактора;
2 – реакционный объем;
3 – мешалка;
4 – штуцер для опорожнения реактора;
5 – загрузочное отверстие;
Т.Н. – теплоноситель или хладагент, поступающий в теплообменную рубашку.

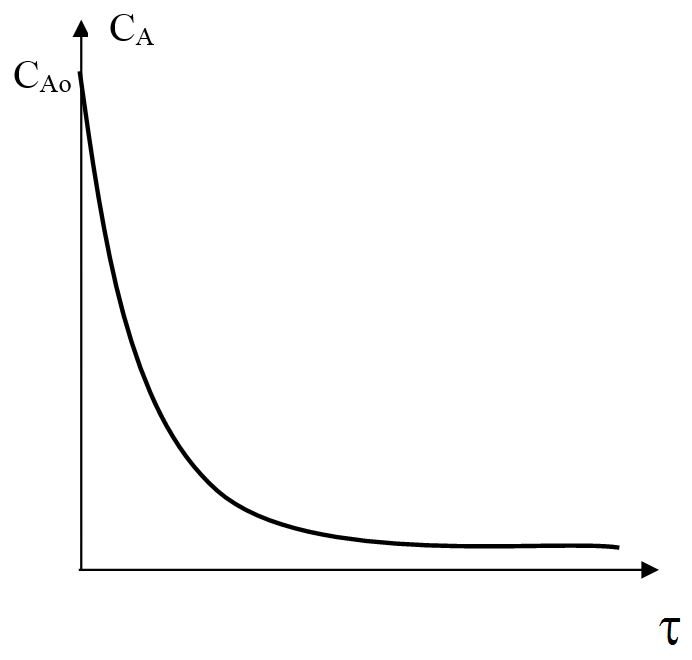
РИС-П работает в нестационарном режиме, т.е. в разные моменты времени условия в периодическом реакторе разные (концентрация реагентов, продуктов, скорость реакции и т. д.). Однако в каждый момент времени в силу допущения об идеальности эти параметры одинаковы во всем объеме реактора.

Исходя из допущений об идеальности РИС-П, за элементарный объем аппарата принимают весь реакционный объем (V_p). Так как РИС-П работает в нестационарном режиме, за элементарный промежуток времени принимают бесконечно малую величину dτ.

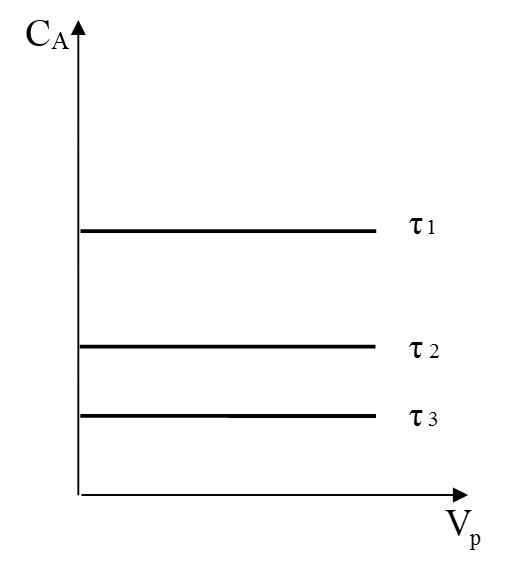Изменение концентрации реагента А в реакторе идеального смешения периодического действия во времени процесса и в объеме в разные моменты времени

В реальных условиях приблизиться к режиму идеального смешения можно, применяя интенсивное перемешивание реакционной смеси. Наряду с этим, форма и размеры емкостного аппарата должны быть оптимальными для уменьшения объема застойных зон.

Материальный баланс РИС-П

Материальный баланс показывает изменение количества реагента или продукта за счёт его поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени. Материальный баланс РИС-П составляют на стадию химической реакции при отсутствии подачи реагентов и отвода продуктов (N_Aвх = N_Aвых= 0).

Запишем материальный баланс РИС-П по взятому в недостатке реагенту A:

Здесь N_Aх.р − количество (в молях) реагента A, расходуемого на протекание химической реакции в элементарном объёме за элементарный промежуток времени,

N_Aнак − количество (в молях) реагента A, накопленное вэлементарном объёме за элементарный промежуток времени.

Входящие в состав материального баланса РИС-П слагаемые могут быть выражены через параметры процесса следующим образом:

(здесь W_A − скорость химической реакции по компоненту A, V_р − реакционный объём реактора, dτ − элементарный промежуток времени),

(здесь V_р − реакционный объём реактора, dC_A − изменение концентрации реагента A в элементарном объёме за элементарный промежуток времени).

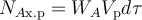
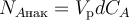
При подстановке полученных выражений в уравнение материального баланса РИС-П получим:

Преобразуем выражение, сократив на реакционный объём реактораV_р:

Выразим отсюда элементарный промежуток времени dτ:

Проинтегрировав dτ на интервале от 0 до τ_х.р, рассчитаем полное время протекания химической реакции в РИС-П τ_х.р:

Учитывая, что , получаем характеристическое уравнение РИС-П:

Тепловой баланс РИС-П

Тепловой баланс показывает изменение количества теплоты за счёт её поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени. Тепловой баланс РИС-П составляют на стадию химической реакции при отсутствии подачи реагентов и отвода продуктов (Q_вх = Q_вых = 0).

Запишем тепловой баланс политермического РИС-П:

Здесь Q_х.р − количество теплоты, выделяющейся (со знаком плюс) или поглощаемой (со знаком минус) при протекании химической реакции в элементарном объёме за элементарный промежуток времени,

Q_т.о − количество теплоты, вносимой (со знаком плюс) в элементарный объём или отводимой (со знаком минус) из него за счёт теплообмена с теплоносителем или хладагентом за элементарный промежуток времени,

Q_нак − количество теплоты, накопленное в элементарном объёме за элементарный промежуток времени.

Входящие в состав теплового баланса РИС-П слагаемые могут быть выражены через параметры процесса следующим образом:

(здесь ΔH − тепловой эффект химической реакции, W_A − скорость химической реакции по компоненту A, V_р − реакционный объём реактора, dτ − элементарный промежуток времени)

(здесь K_т − коэффициент теплопередачи между теплоносителем или хладагентом и реакционной массой, F − поверхность теплообмена между теплоносителем или хладагентом и реакционной массой, ΔT− положительная разность температур между теплоносителем или хладагентом и реакционной массой, dτ − элементарный промежуток времени)

(здесь ρ − плотность реакционной массы в реакционном объёме реактора, V_р − реакционный объём реактора, c_p − удельная теплоёмкость реакционной массы в реакционном объёме реактора,dT − изменение температуры в реакционном объёме реактора за элементарный промежуток времени dτ)

При подстановке полученных выражений в уравнение теплового баланса РИС-П получим:

Преобразуем выражение, разделив на реакционный объём реактораV_р:

Выразим из материального баланса РИС-П скорость реакцииW_A:

Подставим это выражение в тепловой баланс и разделим все слагаемые на C_Ao:

Учитывая, что мольная теплоёмкость с ‘ _p может быть рассчитана по формуле 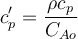, получим конечное выражение теплового баланса для политермического РИС-П:

В случае адиабатического теплового режима, характеризующегося отсутствием теплообмена реакционной смеси с теплоносителем или хладагентом (тепловая изоляция реактора), тепловой баланс РИС-П примет вид:

=> вся теплота, выделяемая или поглощаемая в ходе химической реакции, идёт на изменение температуры реакционной смеси.

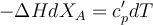
В случае изотермического теплового режима, характеризующегося постоянством температуры реакционной смеси (dT = 0) получим:

=> вся теплота, выделяемая или поглощаемая в ходе химической реакции, компенсируется теплообменом с хладагентом или теплоносителем.

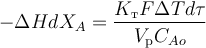
Видео:Процессы и аппараты. Материальный балансСкачать

Уравнение материального баланса для реактора идеального смешения

к списку лекций

к списку предметов

Идеальные химические реакторы.

Эффективность любого химического процесса, выражаемая показателями производительности и селективности, в значительной степени определяется кинетической моделью процесса. В свою очередь характер этой модели определяет тип реактора, при котором достигается наиболее высокое значение указанных показателей. Наиболее удобно выявит влияние типа реактора на тот или иной процесс и его показатели на примере идеальных реакторов.

Классификация химических реакторов, основанная на структуре потока реакционной массы, различает идеальный реактор периодического действия, непрерывный реактор идеального вытеснения и непрерывный реактор идеального смешения.

Идеальный периодический реактор может быть представлен как емкостной аппарат, снабженный мешалкой, число оборотов которой обеспечивает равенство концентраций компонентов реакции в любой точке объема, и постоянство температуры по объему ( ).

Дополнительное условие идеальности такого реактора состоит в одновременной и моментальной загрузке всех компонентов исходной смеси.

Скорость протекания реакции в таком реакторе во времени определяется выражением

(1)

Для периодических реакторов реакционный объем обычно постоянен и тогда уравнение (1) приобретает простой вид

(2)

Из последнего выражения следует, что

(3)

Так как , где Х_А – степень превращения компонента А, то

Уравнение (3) переходит в вид

(4)

Уравнение (4) является основой для расчета реакторов периодического действия. Оно справедливо для любого компонента простой и сложной реакции, причем для нахождения интеграла надо подставить в него функцию .

Рассчитать реакционный объем периодического производства этилацетата с ежесуточной производительностью 50 т этилацетата в сутки.

, где k =7,93·10 — 6 м 3 кмоль -1 сек -1 , К=2,93.

Мольные скорости превращения каждого из компонентов равны вследствие равенства стехиометрических коэффициентов. Загружаемый водный раствор содержит 25 мас. % кислоты, 46 мас. % спирта и не содержит эфира. Степень превращения кислоты равна 35 %. Плотность реакционной массы постоянна и составляет r =1020 кг/м 2 . Установка должна работать круглосуточно. Время загрузки, разгрузки и очистки реактора составляет 1 ч не зависимо от размеров реактора. Каков необходимый объем реакционной зоны, если использовать а) один реактор, б) три реактора?

Основой для расчета является выражение (1)

Рассчитаем концентрации компонентов реакционной массы в исходном растворе, исходя из объема 1 м 3 .

В соответствии с кинетическим уравнением скорость реакции выразится как

где

Подставляем окончательное выражение r_A в уравнение (1) и производим численное интегрирование полученной функции в пределах от Х=0 до Х=0,35.

В результате интегрирования получаем .

Время одной технологической операции составляет 2+1=3 часа. Таким образом, каждые 24 часа можно провести 24:3=8 операций.

Ежесуточное производство этилацетата на 1 м 3 реакционного объема составляет

Тогда общий реакционный объем составит

Таким образом, для обеспечения необходимой производительности необходимо использовать единичный реактор объемом 52 м 3 . Учитывая степень заполнения реактора 70 %, общий объем реактора составит . Согласно условию задачи, эту же производительность можно обеспечить тремя реакторами объемом .

В непрерывном реакторе идеального вытеснения реакционная масса движется вдоль оси потока, вытесняя последующие слои. Условие идеальности такого аппарата состоит в том, что каждый элемент реакционной массы в данном поперечном сечении движется вдоль оси потока с одинаковой скоростью

В этой модели исключается торможение потока насадкой или стенками и диффузионные явления, из которых особенно существенно обратное или продольное перемешивание потока. При стационарном режиме работы, т.е. при постоянных во времени скорости, составе поступающей смеси и температуре, каждый элемент реакционной массы пребывает в реакторе идеального вытеснения одинаковое время, а концентрации реагентов и температура в каждом поперечном сечении остаются постоянными. В этом случае концентрации меняются только по длине аппарата, что позволяет составить дифференциальное уравнение материального баланса для элементарного объема dV в единицу времени

Интегрирование этого уравнения по всему реакционному объему V , когда количество вещества меняется от до F_A дает:

(5)

Так как , то это уравнение можно привести к виду

(6)

(7)

Обратная величина левой части последнего уравнения представляет собой удельную нагрузку реактора по реагенту А (число молей этого реагента в единицу времени на единицу реакционного объема).

Умножая обе части уравнения (7) на , получаем

(8)

Сравнение полученного уравнения с уравнением (4) для периодического идеального реактора показывает полную идентичность их правой части. В то же время выражение для левой части уравнения также имеет размерность времени, при этом величина представляет собой объемную скорость реакционного потока на входе в реактор. Тогда левая часть представляет собой время контакта

В этом случае уравнение (8) приобретает вид

(9)

полностью идентичный уравнению (4) для периодического идеального реактора. В общем случае величину контакта называют условным временем.

Рассчитать объем реактора идеального вытеснения при тех же условиях, что и в предыдущей задаче.

Принимаем, что время контакта в реакторе вытеснения такое же, что и в периодическом реакторе τ =7270 сек., мольная скорость потока продукта рассчитывается как

Непрерывный реактор полного смешения (б) отличается тем, что в нем реакционная масса интенсивно перемешивается. Условием его идеальности является отсутствие градиентов концентраций и температуры по объему , а при стационарном режиме концентрации и температуры постоянны и во времени. В таком аппарате концентрация вещества в исходной смеси С _{i 0} моментально падает (из-за разбавления в большом объеме реакционной массы до некоторой величины С _i , равной его концентрации в смеси, выходящей из реактора. Эта особенность реактора полного смешения дает возможность при стационарных условиях работы составить уравнение материального баланса в целом по аппарату (минус дифференциальные выражения)

(10)

Так как , то , откуда следует, что

(11)

Таким образом, в стационарном режиме работа реактора идеального смешения характеризуется алгебраическим уравнением. Реакторы идеального смешения называются безградиентными в отличие от интегральных реакторов периодического действия и идеального вытеснения, где концентрации и скорости реакций переменны – в первом случае во времени, во втором – по длине реактора, которая также пропорциональна времени реакции.

Умножая левую и правую части уравнения (11) на С_{А 0}

(12)

Если объем смеси во время проведения реакции не меняется, то

(13)

где τ – истинное время контакта.

Емкость с полезным объемом в 52 м 3 , описанная в задаче 1, используется в качестве реактора непрерывного действия в режиме полного смешения. Состав загрузки и степень полного превращения уксусной кислоты составляет также 35 %. Какова производительность по этилацетату в это случае? Какой объем должен иметь реактор для производства 50 м 3 этилацетата в сутки?

В решении к задаче 1 были получены мольные концентрации при Х_А=0,35. Их можно использовать для расчета скорости реакции r_A .

Тогда массовая скорость производства эфира

Общая скорость производства в реакторе 52 м 3 составляет

Для того чтобы обеспечить производительность 50 т/сутки, необходимо взять пропорционально больший реактор, т.е. , т.е. значительно больше, чем в случае реактора идеального вытеснения или идеального периодического реактора.

Сравнение эффективности проточных реакторов

идеального смешения и идеального вытеснения.

Сравним производительность идеальных проточных реакторов для случая проведения в них простых реакций, не осложненных побочными взаимодействиями. Зададимся одинаковой степенью превращения ключевого реагента и будем считать более эффективным тот реактор, для которого для достижения заданных результатов требуется меньшее время пребывания .

Для проточного реактора идеального смешения при заданной глубине превращения среднее время пребывания в соответствии с уравнением (13) можно определить как произведение двух постоянных величин

т.е. геометрически представить в виде прямоугольника с соответствующими сторонами.

Для стационарного реактора идеального вытеснения

т.е. величина τ как определенный интеграл выражается геометрической площадью, ограниченной прямыми С_А и С_{А 0}, графиком функции и осью абсцисс. Из рисунка видно, что площади, соответствующие времени пребывания в реакторе вытеснения, заметно меньше площади, соответствующей времени в реакторе смешения для достижения одного и того же результата. Следовательно, при равном объемном расходе реактор идеального вытеснения должен иметь меньший объем. Таким образом, реакторы идеального вытеснения характеризуются более высокой производительностью, чем реакторы идеального смешения.

Другим важным критерием эффективности реакторов является селективность процесса. Рассмотрев в этой связи ряд случаев, определяющих выбор в пользу реактора смешения или вытеснения.

1. Система параллельных реакций (основной и побочной), когда порядок побочной реакции по реагенту выше, чем основной

Рассмотрим кинетические зависимости для реагента А в реакторах смешения и вытеснения. Из этих зависимостей видно, что действующая концентраций в реакторе смешения С_А будет существенно ниже по сравнению со средней концентрацией А в реакторе вытеснения.

Это означает, что побочная реакция буде более успешно конкурировать с основной в реакторе смешения, т.е. селективность в этом реакторе буде ниже. Поэтому, если побочная реакция имеет более высокий порядок по реагенту, чем основная, то более выгодно для достижения более высокой селективности работать в реакторе смешения.

2. Система параллельных реакций (основной и побочной), когда порядок побочной реакции по реагенту ниже, чем основной, n m . В этом случае большее значение эффективной концентрации в реакторе вытеснения обеспечит более успешную конкуренцию основной реакции по сравнению с побочной. В этом случае более высокая селективность будет достигнута в реакторе вытеснения.

3. Система параллельных реакций (основной и побочной), когда порядки основной и побочных реакций по реагенту одинаковы, m = n .

В этом случае выход целевого продукта не зависит от типа реактора.

4. Система последовательных реакций

в которых В- основной продукт, С – побочный.

Очевидно, что в случае реактора смешения концентрация основного продукта в реакционной массе будет выше средней концентрации В в реакторе вытеснения. По этой причине в реакторе смешения скорость побочной реакции будет существенно выше, а селективность – ниже по сравнению с реактором вытеснения. Поэтому для достижения высоких селективностей последовательных реакций более выгодным является реактор вытеснения.

Таким образом, в ряде случаев для достижения высокого выхода целевого продукта эффективнее реактор идеального вытеснения, а иногда – реактор идеального смешения.

При выборе в пользу того или иного типа реактора необходимо также учитывать чисто эксплуатационные реакторы. К ним следует отнести большое гидравлическое сопротивление трубчатых реакторов, трудность чистки таких аппаратов. Реакторы смешения с интенсивным перемешиванием проще по конструкции и обеспечивают более эффективный подвод или съем тепла. В то же время они обладают низкой производительностью. Чтобы использовать преимущества реакторов смешения и вытеснения, используют каскад реакторов идеального смешения путем последовательного включения в технологическую нитку нескольких реакторов.

Каскад реакторов смешения.

Примером каскада реакторов является последовательная цепь емкостных аппаратов с мешалками.

Примером подобной модели может быть не только система последовательно расположенных отдельных аппаратов, но и проточный реактор тем или иным способом разделенный на секции, в каждой из которых осуществляется перемешивание реакционной смеси. В частности, близка к такому типу аппарата тарельчатая барботажная колонна.

Для каскада реакторов идеального смешения должны выполняться следующие допущения об идеальности.

1. В каждой секции каскада выполняется условие реактора идеального смешения, т.е. мгновенное изменение параметров процесса, равенство параметров во всех точках секции и в потоке, выходящем из нее.

2. Отсутствие обратного влияния: каждый последующий реактор не влияет на предыдущий.

Математическая модель каскада реакторов идеального смешения, работающего в изотермическом режиме, представляет собой систему уравнений материального баланса по какому-либо участнику реакции, включающему по меньшей мере n Уравнений по числу секций каскада. Если составляется модель для сложной реакции, где недостаточно материального баланса только по одному участнику реакции, число уравнений математической модели кратно n .

Рассмотрим производительность каскада прямоточных реакторов полного смешения, взяв для примера простейшую реакцию первого порядка с участием реагента А.

Для каждого единичного реактора каскада можно записать в соответствии с уравнением (11)

(14)

Умножим обе части уравнения (14) на С_{А 0} и примем, что реакция идет без изменения объема, а все реакторы имеют одинаковый объем. Тогда имеем

, откуда

Соответственно, для первого и второго реакторов каскада

Очевидно, что для всей последовательности из n аппаратов (при ) выражение будет следующим

(15)

Суммарное время контакта во всех реакторах общим объемом составит

т.к. в соответствии с (15)

откуда следует .

Отсюда производительность каскада (по реагенту А) равна

(16)

Так как , то .

Подставляя последнее выражение в уравнение (16), имеем

В то же время производительность единичного реактора вытеснения, заменяющего каскад,

(17)

Для реакции первого порядка, протекающей в реакторе идеального вытеснения в соответствии с уравнением (7)

Подставляя из последнего выражения в уравнение (17), имеем

Тогда соотношение производительностей каскада реакторов смешения и РИВ

Значения относительной эффективности каскада для реакции 1-го порядка рассчитаны для разных n при Х_А=0,95.

Можно видеть, что каскад из n реакторов идеального смешения значительно эффективнее, чем единичный реактор данного типа, причем с увеличением n каскад по удельной производительности все более приближается к модели идеального вытеснения. Это иллюстрируется кинетическими зависимостями для каскада с различным n и РИВ.

Если в реакторах вытеснения происходит частичное перемешивание реакционной массы, происходит выравнивание концентраций и скоростей по реакционному объему. В реальных реакторах такое выравнивание происходит в результате диффузии и конвекции. В этом отношении особенно нежелательна диффузия вдоль оси потока, называемая продольным (или обратным) перемешиванием, ведущая к более пологой кривой концентраций и снижению «средней» скорости и удельной производительности (см. ниже).

Из изложенного следует, что при непрерывном осуществлении гомогенных реакций всякое перемешивание реакционной массы, как правило, снижает удельную производительность реактора. Чтобы уменьшить эти нежелательные эффекты в реальных аппаратах, стараются увеличить отношение их длины (высоты) к диаметру, разделяют аппарат поперечными перегородками, исключают искусственное перемешивание и циркуляцию реакционной массы.

Из уравнения можно рассчитать число секций заданного объема, необходимых для достижения заданной степени превращения Х_А:

(18)

Если полученное при расчете по уравнению (18) число n является дробным, то его округляют в большую сторону, чтобы было выполнено условие , соответствующее числу секций в каскаде.

Если возникает обратная задача определения числа секций, необходимого для достижения заданной степени превращения Х_А (С_А), графическое построение продолжают до тех пор, пока абсцисса точки пересечения прямой