1.3. Уравнение состояния идеального газа
Вид уравнений состояний (1.1) для реальных веществ достаточно сложен.
В связи с этим в термодинамике используются упрощенные физические модели рабочих тел.
Для рабочих тел в газообразном состоянии самой простой и исторически первой является модель идеального газа . Под идеальным газом понимается газ, в котором силы межмолекулярного взаимодействия (притяжение и отталкивание) отсутствуют, а сами молекулы рассматриваются как материальные точки. Идеальный газ подчиняется уравнению Клайперона – Менделеева
где m – масса газа в системе; μ – молярная масса газа; R μ = 8314 Дж/(кмоль·К) – универсальная газовая постоянная, которая не зависит ни от вида газа, ни от условий его существования. Уравнение состояния (1.2) получено путем объединения законов Бойля-Мариотта и Гей-Люссака с учетом закона Авогадро .
Молярная масса μ = m /n , кг/моль, – масса вещества, взятого в количестве одного моля. 1 моль – это единица количества вещества, в которой содержится столько же частиц, сколько в 12 граммах углерода. Количество вещества – n = N/N A , моль, где N – число частиц (атомов, молекул), N A ≈ 6,02·10 23 – число атомов в 12 граммах углерода (число Авогадро ). Численно μ = Мr·10 -3 , где Mr – относительная молекулярная масса вещества (табл. Менделеева ) (например: =2 кг/кмоль).
В удельных величинах (т.е. для 1 кг газа) уравнение (1.2) будет иметь вид
где R – удельная газовая постоянная, Дж/(кг·К).
Поясним физический смысл удельной газовой постоянной R . Для первого состояния уравнение (1.2) запишется в виде , для второго состояния при том же давлении – . Вычтем из второго уравнения первое и найдем, что , т.е. удельная газовая постоянная есть работа, совершаемая 1 кг газа при его нагреве на 1 градус при постоянном давлении.
Экспериментальные данные показывают, что реальный газ тем ближе к идеальному, чем ниже его плотность. Другими совами, с уменьшением объема данного количества газа, вызываемым повышением давления или понижением температуры, любой газ будет давать все большие отклонения от свойств идеального газа. Таким образом, под понятие «идеальный газ» подходят все реальные газы при высоких температурах и малых давлениях.
В практике зачастую рабочим телом является смесь однородных газов (например, воздух), каждый из которых можно считать идеальным и которые не вступают между собой в химические реакции.
Такая смесь также является идеальным газом и подчиняется уравнению состояния (1.2) для смеси
где R=R μ / μ – газовая постоянная смеси; μ –средняя (кажущаяся) молярная масса смеси (условная величина, относящаяся к однородному представляемому газу, у которого число молекул и общая масса равны числу молекул и массе смеси).
Масса смеси равна массе всех составляющих компонент
Основным законом, определяющим поведение газовой смеси является закон Дальтона :
каждый отдельный газ ведет себя в газовой смеси так, как будто он один при температуре смеси занимает весь объем смеси,
каждый отдельный газ, входящий в газовую смесь, имеет такое давление, какое бы он имел бы, если бы он один занимал весь объем газовой смеси.
Отсюда величина р (абсолютное давление смеси) определяется как
где р i – парциальное давление i -го компонента, т.е. давление, которое имел бы i -й компонент, если бы он один занимал весь объем смеси при той же температуре ().
Состав смеси задается массовыми или молярными долями составляющих смесь компонент, а также объемными долями (концентрациями).
Массовой долей называется отношение массы каждого газа к общей массе смеси: .
Из уравнения (1.3) следует, что .
Объемной долей называется отношение парциального объема (объем, который занимал бы газ, если его давление и температура равнялись давлению и температуре смеси газов, т.е. ) к общему объему смеси газов: . Из определений парциальных давления и объема и постоянства температуры следует:

Просуммировав последнее равенство по всем компонентам смеси, получим , т.е. сумма парциальных объемов газов, составляющих смесь, равна объему смеси газов.
Сумма объемных долей равна единице: .
Молярной долей компонента называют отношение количества вещества каждого газа n i к количеству вещества смеси газов n . Из соотношений и и закона Авогадро (в равных объемах разных идеальных газов, находящихся при одинаковых температурах и одинаковых давлениях, заключено равное число молекул, т.е. ) следует:
т.е. задание смеси молярными долями равнозначно заданию ее объемными долями.
Массовые и объемные доли связаны соотношением:

Если смесь задана массовыми долями g i , то газовая постоянная смеси и молярная масса смеси вычисляются следующим образом:
Если смесь задана объемными долями r i , то формулы для вычисления молярной массы смеси и газовой постоянной смеси следующие:

Парциальные давления и объемы газов определяются по закону Бойля –Мариотта (при постоянной температуре газа произведение давления газа на его объем есть величина постоянная, т.е.):

Международная система единиц (СИ) и ее основные единицы.
Основные термодинамические параметры и их размерность.
Что понимают под равновесным состоянием термодинамической системы?
Понятие равновесного и неравновесного состояний.
Что такое уравнение состояния системы?
Геометрическая интерпретация состояния системы, термодинамического процесса.
Что называется идеальным газом? В чем отличие идеального газа от реального?
Что такое газовая постоянная? Ее физический смысл, размерность и способы определения.
Сообщение рабочему телу теплоты в каком-либо процессе вызывает изменение его состояния и, в общем случае, сопровождается изменением температуры. Изменение температуры, как и любого другого параметра состояния рабочего тела, не зависит от вида процесса, а зависит от его начального (1 ) и конечного (2 ) состояния, т.е. (для элементарного процесса изменение параметра заменяется его дифференциалом ).
Отношение количества теплоты δQ , сообщаемого телу, к изменению температуры тела dT в элементарном термодинамическом процессе называется истинной теплоемкостью тела в данном процессе:
Нижний индекс здесь указывает на то обстоятельство, что теплоемкость так же, как и теплота, зависит от характера процесса. Кроме того, теплоемкость зависит от количества тела и его термодинамического состояния. Следует также отметить, что в данном процессе не меняется химический состав тела, не содержится переход вещества из одного агрегатного состояния в другое, не происходит растворения компонентов и пр.
В зависимости от выбранной единицы количества вещества различают массовую, объемную и мольную удельные теплоемкости:
Наиболее часто на практике используется понятие массовой теплоемкости.
2.1. Истинная и средняя теплоемкости
Теплоемкость реального вещества не является постоянной величиной. Она изменяется с изменением температуры, причем эта зависимость может быть весьма значительной (рис. 2.1).
Удельное количество теплоты процесса вычисляется по формуле
Применяют следующие способы по определению этой величины:
по результатам эксперимента зависимость теплоемкости от температуры представляют в виде аппроксимационного полинома
где – коэффициенты аппроксимации. В справочной литературе приводятся эти коэффициенты. Тогда
в практических расчетах в интервале температур t 1 , t 2 теплоемкость считают постоянной величиной, равной
которую называют средней теплоемкостью в данном интервале в отличие от истинной теплоемкости, введенной в (2.1). В справочных данных приводятся средние теплоемкости от 0 до фиксированной температуры t , полученные опытным путем, т.е.
Среднюю теплоемкость в интервале температур t 1 , t 2 по этим справочным данным можно вычислить по формуле
Тогда удельное количество теплоты процесса определится как
2.2. Изохорная и изобарная теплоемкости
В термодинамике имеют большое значение
равная отношению количества теплоты в процессе при постоянном объеме к изменению температуры тела,
равная отношению количества теплоты в процессе при постоянном давлении к изменению температуры тела.
В теплотехнических расчетах используют таблицы, в которых приводятся полученные опытным путем числовые значения удельных изобарной и изохорной теплоемкостей для различных веществ в зависимости от температуры.
2.3. Теплоемкость смесей газов
При расчетах часто приходится иметь дело со смесями газов, а в таблицах приводятся теплоемкости только для отдельных газов.
Если смесь газов задана массовыми долями g i , то удельные массовые теплоемкости смеси определяются по формулам
Если смесь газов задана объемными долями r i , то удельные объемные теплоемкости смеси определяются по формулам
Выпишите единицы измерения удельной теплоемкости.
Как вводится понятие средней теплоемкости?
3. Закон сохранения и превращения энергии
Понятие энергии связано с движением материи.
Энергия может принимать многие формы – механической работы, теплоты, химической энергии, энергии электрического и магнитного полей.
В термодинамическом процессе взаимодействие окружающей среды и закрытой термодинамической системы осуществляется путем обмена энергией в форме теплоты и механической работы.
3.1. Внутренняя энергия
Любая среда обладает некоторым запасом внутренней энергией U (Дж), которую в технической термодинамике представляют как сумму кинетической и потенциальной энергий молекул и атомов среды. Кинетическая энергия этих частиц определяется их скоростью и массой, потенциальная – силами взаимодействия между ними, которые зависят от их взаимного расположения. Внутренняя энергия системы – это энергия, заключенная в самой системе. Значит, внутренняя энергия может характеризовать состояние тела наряду с величинами р , V , T .
Внутренняя энергия обладает свойством аддитивности, т.е. внутренняя энергия сложной системы равна сумме внутренних энергий составляющих её частей:
Внутренняя энергия 1 кг вещества называется удельной внутренней энергией u = U / m (Дж/кг).
Для большинства технических приложений термодинамики важно не абсолютное значение U , а изменение этой величины. Поэтому количественное определение внутренней энергии однородной системы часто определяется по отношению к некоторому условно выбранному стандартному состоянию.
3.2. Закон сохранения энергии в термодинамике
Совершая термодинамический процесс, закрытая система взаимодействует с внешней средой (внешними телами и полями), т.е. обменивается энергией. В технической термодинамике рассматриваются два вида передачи энергии – путем передачи теплоты и совершением механической работы.
Передача теплоты происходит между телами, имеющими различную температуру и приведенными в соприкосновение, или между телами с различными температурами, находящимися на расстоянии, посредством электромагнитных волн (тепловое излучение). Передача теплоты происходит на молекулярном (микрофизическом) уровне без видимого движения тел.
Передача энергии в форме работы происходит с перемещением всего тела или его части в пространстве. При этом способе тело либо движется в силовом поле, либо изменяет свой объем под действием внешнего давления. Работа представляет собой макрофизическую форму передачи энергии.
Следует заметить, что теплота и работа в отличие от энергии тела не являются функциями его состояния, а зависят от вида процесса, определяют этот процесс, т.е. являются функциями самого процесса.
Многочисленные опыты и наблюдения привели к открытию фундаментального закона природы – закону сохранения энергии: энергия в природе не возникает из ничего и не исчезает, или количество энергии неизменно, она только переходит из одной формы в другую, или
где Q – теплота, участвующая в процессе; L – совершаемая работа; ΔЕ – изменение энергии системы. Здесь и далее условимся считать:
работу положительной , если эта работа совершается рабочим телом, и отрицательной , если совершается работа над рабочим телом системы;
теплоту, подведенную к телу, – положительной , а отведенную – отрицательной,
кроме того, изменение любого параметра состояния в конечном процессе будем обозначать символом Δ (дельта), а в элементарном процессе – d (дифференциал соответствующего параметра). При любом конечном термодинамическом процессе изменение параметра состояния (давление, температура, внутренняя энергия, энтальпия, энтропия и т.д.) не зависит от вида процесса, а определяется начальным и конечным состоянием.
В общем случае термодинамическая система обладает внутренней энергией U , кинетической энергией (в термодинамике система рассматривается как целое, движущееся со скоростью w ) – mw 2 /2, потенциальной – mgz (z – высота, на которой находится система). Изменение полной энергии в процессе 1 –2 можно представить как:
Работа, совершаемая в этом процессе, складывается из работы L об, связанной с изменением объема рабочего тела системы (деформационная работа), работы L дв по перемещению системы в пространстве, технической работы L тех (при перемещении системы в различных технических устройств, например, в двигателе, паровом котле, компрессоре и т.п.), работы против сил трения L тр:
L = L об + L дв + L тех + L тр.
Теплота, участвующая в процессе, представляет собой сумму теплоты Q внеш, задействованной в обмене с внешней средой, и теплоты трения Q тр:
Учитывая, что Q тр = L тр (многочисленные эксперименты показали, что работа потока, затраченная на преодоление трения, полностью превращается в теплоту, воспринимаемую потоком), закон сохранения энергии в термодинамике для 1 кг рабочего однородного вещества (т.е. в удельных массовых величинах) в элементарном процессе можно записать:

(индекс внеш пропущен за ненадобностью).
Следует подчеркнуть, что в правой части (3.1) под знаком дифференциала находятся функции состояния, а остальные – величины, зависящие от характера протекания термодинамического процесса. Так как работа и теплота являются функциями процесса, а не функциями состояния, то знак δ обозначает лишь тот факт, что в элементарном процессе величины, следующие за ним – произвольные бесконечно малые, а не приращения каких-либо определенных функций. Таким образом, δq и δl –элементарные (т.е. соответствующие бесконечно малым изменениям состояния системы) количества теплоты и работы.
Если термодинамическая система не меняет своего положения в пространстве и единственным видом работы является работа, связанная с изменением объема системы, то уравнение (3.1) принимает более простой вид:
Работа δl об совершается либо против сил внешнего давления и, тогда, объем рабочего тела расширяется, либо, наоборот, внешняя среда совершает работу над телом, сжимая его. Для равновесных процессов, когда давление среды равно давлению в рабочем теле, эта работа вычисляется как р dv , где v – удельный объем рабочего вещества.
называют первым началом термодинамики: подведенная к закрытой покоящейся термодинамической системе теплота расходуется на изменение внутренней энергии системы и на совершение работы по изменению объема системы . Балансовое соотношение (3.2) называют еще лекций по теоретическому литературоведению. 1. Барокко: .
- Л. А. Елисеева © Федеральное государственное бюджетное учреждение науки Государственная публичная научно-техническая библиотека Сибирского отделения ран (гпнтб со ран), 2013
- Н. В. Басова [и др.];под общ ред. Н. В. Басовой. Ростов н/Д: Феникс, 2008
- Список научных трудов казнму за период 2008 — 1 06 2013 г (1)
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
- Подобные документы
- Газовые смеси
- Уравнение массового состава газовой смеси
- 📺 Видео
Л. А. Елисеева © Федеральное государственное бюджетное учреждение науки Государственная публичная научно-техническая библиотека Сибирского отделения ран (гпнтб со ран), 2013
Случайных блужданий / А. Н. Бородин , И. А. Ибрагимов; под. 241. Дорогокупец П.И. Термодинамика минералов и минеральных равновесий. каталогов: конспект лекции по курсу «Справочно. государственного технического университета. Серия, Технические науки. – .
Н. В. Басова [и др.];под общ ред. Н. В. Басовой. Ростов н/Д: Феникс, 2008
Курс) Письменный Д. Т. Конспект лекций по высшей математике [Текст] : . Техническая термодинамика Рудобашта, С. П. Теплотехника [Текст] : учебник для студ. вузов, обучающихся по . 2008. — 204 с. 10 Бородин , И. Ф. Автоматизация технологических процессов.
Список научных трудов казнму за период 2008 — 1 06 2013 г (1)
. «Рентгенолгические методы исследования» Лекции по клинической онкологии. Алматы. второго закона термодинамики » 2-Международный. и экспертная оценка технического оснащения организаций здравоохранения. академика РАМН Ю.И. Бородина , Бишкек, 2009,С. .
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
Волгоградский Государственный Технический университет
Кировский вечерний факультет
Семестровая работа по дисциплине:
ТОПЛИВО, ГАЗОВЫЕ СМЕСИ И ТЕПЛОЕМКОСТЬ
Выполнил: студент гр.ТВБ-385
Проверил: доц. Горюнов В.А.
топливо сжигание температура окислитель
В промышленной печи при постоянном давлении сжигают топливо (этанол). В качестве окислителя используют воздух с температурой T 1 =660К. Заданы коэффициенты избытка воздуха: а= 1,0 и коэффициент полноты сгорания топлива ж =0,9. Определить теоретическое значение максимальной температуры горения Тг. Теплотой, вносимой топливом, пренебречь.
Таб. №1. Состав и теплота сгорания топлива
Таб. №2. Формулы средних изохорных массовых теплоемкостей (c v)
0,691 + 7,1*10 — 5 Т
0,775 + 11,7*10 -5 Т
1,328 + 28,07*10 -5 Т
0,716 + 7,54*10 -5 Т
0,628 + 6,75*10 -5 Т
Таб. №3. Результаты расчета
Максимальная теоретическая температура сгорания находится с помощью уравнения теплового баланса:
где: Q o — Теплота, вносимая окислителем;
Qh — Низшая теплота сгорания топлива;
ж — Коэффициент полноты сгорания топлива;
Qn. Сг- Теплота, полученная продуктами сгорания;
Находим теплоту, выделяющуюся при сжигании топлива (жQ h).
Из таблицы 2 берется значение Q h:
Q h =27100 кДж/кг
Из таблицы 1 берется значение ж (в моём варианте ж=0,9)
ж *Q H =0,9*27100=24390 кДж/кг
Находим теплоту, вносимую окислителем:
Q o = С р. возд. *m возд* T 1
Определяем среднюю изохорную массовую теплоемкость воздуха по формуле, приведенной в таблице №2
c v возд= 0,691 + 7,1*10 -5 *660=0,73786 кДж/кг*К
Вычисляем среднюю изобарную массовую теплоемкость по формуле Майера:
Ср возд= c v возд +R=0.73786+0.287=1.02486 кДж/кг*К
Определяем теоретически необходимую массу воздуха:
m o возд=2,67* C p +8H p — O p /0,23= (2,67*0,52+8*0,13-0,35)/0,23= (1,3884+1,04-0,35)/0,23=2,0784/0,23=9,0365 Кг/Кг
Определяем действительную массу воздуха:
m возд =а*m o возд =1,0*9,0365 =9,0365 Кг/Кг
Q o =С р. возд. *m возд* T 1 =1.02486*9,0365*660=6112.36 кДж/кг
Вычисляем теплоту, внесённую окислителем и сгоревшим топливом:
жQ H +Q o =24390+6112.36=30502.36 кДж/кг
Находим теплоту продуктов сгорания (Qn.Сг):
Q n . Сг = С Р, п.сг*m п, сг * T 2 .
а) Определяем массу продуктов сгорания:
m п, сг =1+m возд =1+9,0365=10.0365
b) Вычисляем массовые доли компонентов в продуктах сгорания:
g co 2 =m co 2 /m п, сг =3.67*С Р / m п, сг =3.67*0.52/10.0365=0.1901
g H 2 o =m H 2 o / m п, сг =9*H p / m п, сг =9*0.13/10.0365=0.1166
g o2 =m o2 /m п, сг =0.23*(a-1) *m o возд /m п, сг =0.23*(1.0-1) *9,0365/ 10.0365=0
g N2 =m N2 /m п, сг =0.77*a*m o возд /m п, сг =0.77*1.0*9,0365/10.0365 = =0.693
c) Находим среднюю изобарную массовую теплоемкость продуктов сгорания по формуле:
С Р, п. сг= g (co 2) * С р(co 2) + g (H 2 o) * С р (H 2 O) + g (o 2) * С р(O 2) + g (N 2) * С р(N 2) =
Находим изобарные теплоемкости компонентов продуктов сгорания:
a) c v(co 2) = 0,775 + 11,7*10 -5 *Т 2
b) c v(H2 o) =1.328+28.07*10 -5 *Т 2
c) c v(O 2) =0.628+6.75*10 -5 *Т 2
d) c v(N 2) =0.716+7.54*10 -5 *Т 2
Используя формулу Майера находим с р. :
1. С р (co 2) =c v(co 2) +R=0.775+11.7*10 -5 *Т 2 +0.189=0.964+11.7*10 -5 *Т 2
2. С р (H2O) = c v(H2 o) +R=1.328+28.07*10 -5 *Т 2 +0.462=1.79+28.07*10 -5 *Т 2
3. С р (O 2) = c v(O 2) +R=0.628+6.75*10 -5 *Т 2 +0.260=0.888+6.75*10 -5 *Т 2
4. С р (N 2) = c v(N 2) +R=0.716+7.54*10 -5 *Т 2 +0.297=1.013+7.54*10 -5 *Т 2
Таким образом находим среднюю изобарную массовую теплоемкость продуктов сгорания по формуле:
С Р, п. сг= g (co 2) * С р(co 2) + g (H 2 o) * С р (H 2 O) + g (o 2) * С р(O 2) + g (N 2) * С р(N 2) =0.1901*(0.964+11.7*10 -5 *Т 2) +0.1166*(1.79+28.07*10 -5 *Т 2) +0*(0.888+6.75*10 -5 *Т 2) +0.693*(1.013+7.54*10 -5 *Т 2) =0,1832+2,2242*10 -5 *Т 2 +0,2087+3,2729*10 -5 *Т 2 +0+0,702+5,2252*10 -5 *Т 2 =1,0939+10,7223*10 -5 *Т 2 =1,0939+10,7223*10 -5 *3934.89= =1.516
Находим теплоту продуктов сгорания Q n . Сг:
Q n . Сг = С Р, п.сг*m п, сг * T 2 =(1,0939+10,7223*10 -5 *Т 2) *10.0365*T 2
Используя уравнение теплового баланса определяем максимальную теоретическую температуру горения(T 2):
24390=(1,0939+10,7223*10 -5 *Т 2) *10.0365*T 2 сокращаем обе стороны на 10.0365:
10.7223*10 -5 *(Т 2) 2 +1.09369*T 2 — 2430.13=0
1.09369 + 1,495/0,000214=1875 К
Размещено на Allbest.ru
Подобные документы
Определение массовой, объемной и мольной теплоемкость газовой смеси. Расчет конвективного коэффициента теплоотдачи и конвективного теплового потока от трубы к воздуху в гараже. Расчет по формуле Д.И. Менделеева низшей и высшей теплоты сгорания топлива.
контрольная работа , добавлен 11.01.2015
Газовые смеси, теплоемкость. Расчет средней молярной и удельной теплоемкости. Основные циклы двигателей внутреннего сгорания. Термический коэффициент полезного действия цикла дизеля. Водяной пар, паросиловые установки. Общее понятие о цикле Ренкина.
курсовая работа , добавлен 01.11.2012
Удельная теплоемкость — отношение теплоты, полученной единицей количества вещества, к изменению температуры. Зависимость количества теплоты от характера процесса, а теплоемкости — от условий его протекания. Термодинамические процессы с идеальным газом.
реферат , добавлен 25.01.2009
Определение теплоты сгорания для газообразного топлива как суммы произведений тепловых эффектов составляющих горючих газов на их количество. Теоретически необходимый расход воздуха для горения природного газа. Определение объёма продуктов горения.
контрольная работа , добавлен 17.11.2010
Молярная масса и массовые теплоемкости газовой смеси. Процесс адиабатного состояния. Параметры рабочего тела в точках цикла. Влияние степени сжатия, повышения давления и изобарного расширения на термический КПД цикла. Процесс отвода теплоты по изохоре.
курсовая работа , добавлен 07.03.2010
Определение расхода воздуха и количества продуктов горения. Расчет состава угольной пыли и коэффициента избытка воздуха при спекании бокситов во вращающихся печах. Использование полуэмпирической формулы Менделеева для вычисления теплоты сгорания топлива.
контрольная работа , добавлен 20.02.2014
Методика расчета горения топлива на воздухе: определение количества кислорода воздуха, продуктов сгорания, теплотворной способности топлива, калориметрической и действительной температуры горения. Горение топлива на воздухе обогащённым кислородом.
курсовая работа , добавлен 08.12.2011
Термодинамика как область физики, исследующая процессы преобразования теплоты в работу и другие виды энергии. Характеристика ключевых особенностей схемы газового термометра. Рассмотрение основных свойств идеального газа. Сущность понятия «теплоемкость».
презентация , добавлен 15.04.2014
Описание котлоагрегата до перевода на другой вид топлива. Характеристика принятых к установке горелок. Обоснование температуры уходящих газов. Расчет объемов воздуха и продуктов сгорания при сжигании двух видов топлива. Тепловой баланс и расход топлива.
дипломная работа , добавлен 13.06.2015
Назначение туннельных сушилок. Состав топлива и расчет воздуха на горение. Определение общего объема продуктов горения при сжигании топлива и теоретической температуры. Технологический расчет сушильного туннеля. Теплотехнический расчет процесса сушки.
В тепловых двигателях (машинах) рабочим телом являются смеси различных газов. Если компоненты смеси не вступают в химические реакции между собой, и каждый компонент подчиняется уравнению состояния Клайперона, то такая смесь рассматривается как идеальный газ.
Для расчета смеси необходимо определить μ см — среднемолярную массу и R c м -удельную газовую постоянную смеси. Для их определения необходимо знать состав смеси, т. е. какие компоненты и в каких количествах образуют данную смесь, какие параметры имеет каждый компонент входящий в смесь.
Каждый компонент смеси ведет себя так, как если бы в смеси не было других газов, занимает весь располагаемый объем, в котором находится смесь, следует своему уравнению состояния и оказывает на стенки свое так называемое парциальное давление, при этом температура всех компонентов смеси одинакова и равна температуре смеси.
По закону Дальтона давление смеси Р равно сумме парциальных давлений отдельных компонентов, входящих в смесь:
где n- число компонентов смеси.
По закону Амага — объем смеси V равен сумме парциальных объемов отдельных компонентов, входящих в смесь при температуре и под давлением смеси:

где — парциальный объем, м 3 ; V- объем смеси, м 3
Состав смеси задают объемными (молярными) или массовыми долями.
Объемная доля i-го компонента — это отношение парциального объема компонента к объему смеси, т. е. , тогда сумма объемных долей компонентов смеси равна 1, т. е. . Если значение заданы в %, то их сумма = 100%.
Молярная доля i-го компонента n i – это отношение числа киломолей компонента N i к числу киломолей смеси N, т. е. , где 
Учитывая, что идеальный газ при одинаковых условиях имеет одинаковый объем киломоля, то после подстановки получаем: , т. е. для идеальных газов молярные и объемные доли численно равны.
Массовая доля i-го компонента — это отношение массы компонента к массе смеси : , отсюда следует, что масса смеси равна сумме масс компонентов , а так же сумма массовых долей компонентов равна 1 (или 100%).
Пересчет объемных долей в массовые и обратно производится на основе следующих соотношений:

где ρ = μ/22,4, кг/м 3 .
Откуда следует, что массовая доля i-го компонента определится из соотношения:

где — плотность смеси, кг/м 3 , — объемная доля i-го компонента.
В дальнейшем можно определить через объемные доли.

Плотность смеси для объемных долей определяется из соотношения



Парциальное давление определяется по формулам:


Уравнения состояния компонентов и смеси в целом имеют вид:


откуда после преобразований получаем для массовых долей


Плотность и удельный объем смеси для массовых долей:
; 
Для расчета парциальных давлений используется формула:

Пересчет массовых долей в объемные выполняется по формуле:

При определении теплоемкости смеси газов исходят из положения о том, что для нагрева (охлаждения) газовой смеси необходимо нагреть (охладить) каждый из компонентов смеси
где Q i =M i c i ∆t – теплота, затраченная на изменение температуры i-го компонента смеси, с i – массовая теплоемкость i-го компонента смеси.
Теплоемкость смеси определяется из соотношения (если смесь задана массовыми долями)


Молярная и объемная теплоемкости для смеси заданной объемными долями определяются



Пример 1.5 Сухой воздух по массе состоит из g О2 =23,3% кислорода и g N 2 =76,6% азота. Определить состав воздуха по объему (r О2 и r N 2) и газовую постоянную смеси.
1. Из табл.1 находим кг/кмоль и кг/кмоль
2. Определяем объемные доли кислорода и азота:
1. Газовая постоянная воздуха (смеси) определится по формуле:

Пример 1.6 . Определить количество теплоты потребное для нагревания газовой смеси массой М=2 кг при Р=const, состоящей в % по массе: , , , , при изменении температуры от t 1 =900 о С до t 2 =1200 о С.
1. Определяем среднюю массовую теплоемкость компонентов, составляющих газовую смесь при Р=const и t 1 =900 о С (из П2):
1,0258 кДж/кг·К; =1,1045 кДж/кг·К;
1,1078 кДж/кг·К; =2,1097 кДж/кг·К;
2. Определяем среднюю массовую теплоемкость компонентов, составляющих газовую смесь при Р=const и t 1 =1200 о С (из П2):
1,0509 кДж/кг·К; =1,153 кДж/кг·К;
1,1359 кДж/кг·К; =2,2106 кДж/кг·К;
3. Определяем среднюю массовую теплоемкость смеси для интервала температур: t 2 =1200 о С и t 1 =900 о С:
4. Количество теплоты для нагревания 2 кг смеси при Р=const:
Первый закон термодинамики устанавливает количественную связь между изменением внутренней энергии системы и механической работой, совершаемой против сил внешнего давления окружающей среды в результате подвода теплоты к рабочему телу.
Для закрытой термодинамической системы уравнение первого закона имеет вид
Теплота, сообщаемая рабочему телу (или системе) идет на приращение ее внутренней энергии (dU), вследствие повышения температуры тела, и на совершение внешней работы (dL), вследствие расширения рабочего тела и увеличения его объема.
Первый закон может быть записан в виде dH=dq+VdP=dq-dL 0 ,
где dL 0 =VdP – элементарная работа изменения давления называется полезной внешней (технической) работой.
dU – изменение внутренней энергии рабочего тела (системы), включающей в себя энергию теплового движения молекул (поступательное, вращательное и колебательное) и потенциальную энергию взаимодействия молекул.
Так как переход системы из одного состояния в другое происходит в результате подвода теплоты, поэтому рабочее тело нагревается и его температура повышается на dT и объем увеличивается на dV.
Повышение температуры тела вызывает увеличение кинетической энергии его частиц, а увеличение объема тела приводит к изменению потенциальной энергии частиц. В результате внутренняя энергия тела увеличивается на dU, поэтому внутренняя энергия U есть функция состояния тела и может быть представлена в виде функции двух независимых параметров U=f 1 (P,V); U=f 2 (P,T), U=f 3 (υ,T). Изменение внутренней энергии в термодинамическом процессе определяется только начальным (U 1) и конечным (U 2) состоянием т. е.
В дифференциальном виде изменение внутренней энергии запишется
а) в функции от удельного объема и температуры
б) в функции от температуры, т.к. , то
Для практических расчетов, в которых необходимо учесть изменение С v от температуры, имеются эмпирические формулы и таблицы удельной внутренней энергии (часто молярной). Для идеальных газов молярная внутренняя энергия смеси U м определяется по формуле

Для смеси заданной массовыми долями . Таким образом внутренняя энергия есть свойство системыи характеризует состояние системы .
Энтальпия – тепловая функция состояния, введенная Камерлинг-Оннесом, (лауреат Нобелевской премии, 1913 г.), представляющая собой сумму внутренней энергии, системы U и произведение давления системы P на ее объем V.
Так как входящие в нее величины являются функциями состояния, поэтому H также функция состояния т. е. Н=f 1 (P,V); H=f 2 (V,T); H=f 3 (P,T).
Изменение энтальпии dH влюбом термодинамическом процессе определяется начальным H 1 и конечном H 2 состоянием и не зависит от характера процесса. Если система содержит 1 кг вещества, то применяется удельная энтальпия , Дж/кг.
Для идеального газа дифференциальное уравнение имеет вид
соответственно удельная энтальпия определяется по формуле
Уравнение первого закона термодинамики dq=dU+Pdυ, когда единственным видом работы является работа расширения Pdυ=d(Pυ)- υdP, тогда dq=d(U+Pυ)-υdP, откуда
Тема: Теплоемкость, энтальпия, смеси идеальных газов, внутренняя энергия, работа, термодинамические процессы.
Цель работы: Закрепление знаний, полученных при теоретическом обучении, приобретение навыков в осуществлении теплотехнических расчетов.
I. Основные определения, формулы и уравнения
1. Смеси идеальных газов
Газовой смесью называется механическая смесь нескольких газов, химически не взаимодействующих между собой. Каждый из газов, входящих в смесь, называется газовым компонентом; ведет себя так, как если бы других газов в смеси не было, т.е. равномерно распределяется по всему объему смеси. Давление, которое оказывает каждый газ смеси на стенки сосуда, называюется парциальным. Основным законом для смесей идеальных газов является закон Дальтона, согласно которому давление смеси равно сумме парциальных давлений газов, образующих смесь:
2. Внутренняя энергия
Внутренняя энергия тела представляет собой совокупность кинетической энергии движения микрочастиц, составляющих тело, и потенциальной энергии их. взаимодействия, определяемой. силами взаимного притяжения или отталкивания. Абсолютную величину внутренней энергии определить не возможно, поэтому в термодинамических расчетах вычесляется не абсолютная величина внутренней энергии, а ее изменение, т.е.

где U 1 и U 2 — внутренняя энергия начального и конечного состояния рабочего тела (газа);
u 1 и и 2 — уд. внутренняя энергия начального и конечного состояния рабочего тела.
Отсюда вытекает, что изменение внутренней энергии не зависит от характера и пути процесса, а определяется состоянием рабочего тела в начале и конце процесса изменения.
Особенностью идеального газа является отсутствие в нем сил молекулярных взаимодействий, а значит и отсутсвие внутренней потенциальной энергии, т.е. U n =0 и и„ = 0. Следовательно, внутренняя энергия идеального газа:
U=U k =f(T) unu u=u k =f(T).
В термодинамике всякое изменение состояния рабочего тела в результате обмена энергией с окружающей средой называется процессом. При этом изменяются основные параметры рабочего тела:
Преобразования теплоты в механическую работу связано с процессом изменения состояния рабочего тела. Процессы изменения состояния газа могут быть процессами расширения и сжатия. Для произвольной массы газа М (кг) работа равна:
L = М l = Мр (v 2 — v 1) = , Дж
где l = р (v 2 -v 1) Дж/кг — работа 1 кг газа или удельная работа.
4. Энтальпия газа,
Энтальпия — это параметр, характеризующий потенциальную энергию связи рабочего тела (газа) с окружающей средой. Энтальпия и удельная энтальпия:
I = U + pV, Дж и i i = и +pv , Дж/кг.
Удельной теплоемкостью называется количество тепла, которое нужно подвести к 1 кг газа, чтобы нагреть его на 1°С в данном интервале температур.
Удельная теплоемкость бывает массовой, объeмной и киломольной. Между массовой С, объемной C и киломольной С теплоемкостями существует связь:

где Vo 22,4 м 3 /кмоль — уд. объем газа при нормальных условиях.
Массовая уд. теплоемкость газовой смеси:
Объемная удельная теплоемкость газовой смеси:
Киломольная удельная теплоемкость газовой смеси:
6.Уравнение для определения количества тепла
Количество тепла, отдаваемое или воспринимаемоен рабочим телом (газом) можно определить по уравнению:
Q = M C m (t 2 -t 1), Дж или Q = VC (t-t), Дж, где М и V — весовое или объемное количество газа, кг или м 3 ;
t u t — температура газа в конце и а начале процесса ° С;
С и С — массовая и объемная средняя уд. теплоемкость газа
При t cp = Дж/кгК или Дж/м 3 К
7. Первый закон термодинамики
Этот закон рассматривает взаимопревращения тепла и механической работы. По этому закону тепло превращается в механическую работу и наоборот, механическая работа в тепло в строго эквивалентных количествах. Уравнение эквивалентности тепла и работы имеет вид:
С учетом принципа эквивалентности тепла и работы, уравнение теплового баланса для произвольной массы газа:
Q = U + L и q =и+l= u –u +l
Атмосферный сухой воздух имеет следующий примерный массовый состав: g 02 =23,2%, g N 2 =76,8%.
Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу, парциальное давление кислорода и азота, если воздуха по барометру Р=101325 Па.
Определяю объемный состав воздуха:


где r – массовая доля;
m — относительная молекулярная масса;
g – объемная доля.
m возд. =m O2 r O2 +m N2 r N2 = 32·0,209 + 28·0,7908=6,688+22,14=28,83;

где R 0 – газовая постоянная.
Определяю парциальные давления различных газов:
P O 2 =P см · r О2 =101325·0,209=21176,9 (Па);
P N 2 =P см · r N 2 =101325·0,7908 = 80127,81 (Па);
где P O 2 , P N 2 – парциальное давление;
P см – давление смеси.
Сосуд разделен перегородкой на 2 части, объемы которых V 1 =1,5 м 3 и V 2 =1,0 м 3 . В первой части объемом V 1 содержится СО 2 при Р 1 =0,5 Мпа и t 1 =30°С; во второй части объемом V 2 содержится О 2 при Р 2 =0,2 Мпа и t 2 =57°С. Определить массовые и объемные доли СО 2 и О 2 , кажущуюся молекулярную массу смеси и ее газовую постоянную после того, как перегородка будет убрана и процесс смешения закончится.
Определяю индивидуальные газовые постоянные:
Для этого определяю относительную молекулярную массу: m(СО 2) =32+12=44; m(О 2)=32;


Согласно характеристическому уравнению Клайперона, определяю массы газов:


Определяю массовые доли:
Определяю объемные доли:
Определяю кажущуюся молекулярную массу воздуха:
m возд. =m О2 r O 2 +m СО2 r СО2 = 32·0,21 + 44·0,79=6,72+34,74=41,48;
Определяю индивидуальную газовую постоянную для воздуха (R):

В сосуде объемом 300л находится кислород при давлении Р 1 =0,2 Мпа и t 1 =20 0 С. Какое количество теплоты нужно подвести, чтобы температура кислорода повысилась до t 2 =300 0 С? Какое давление установится при этом в сосуде? Для расчета принять среднюю объемную удельную теплоемкость кислорода при н.у. С 02 =0,935
По закону Шарля определяю конечное давление процесса:
; 
где Р,Т – параметры газа.
Определяю индивидуальную газовую постоянную для кислорода (R):

Так как процесс изохорный то определяю количество теплоты которое нужно подвести по соответствующей формуле: Q v =M·С cv ·(T 2 -T 1) для этого согласно характеристическому уравнению Клайперона, определяю массу газа

Какое количество теплоты необходимо затратить, чтобы нагреть 2м 3 воздуха при постоянном избыточном давлении Р изб. =0,2 МПа от температуры 100 0 С до температуры 500 0 С. Какую работу при этом совершит воздух? Для расчета принять: давление атмосферы Р ат. =0,1 Мпа, среднюю массовую изобарную теплоемкость воздуха С pm =1,022 
Определяю индивидуальную газовую постоянную для воздуха:

Абсолютное давление равно сумме избыточного и атмосферного Р=Р изб. +Р ат. =0,1+0,2=0,3 МПа

Так как процесс изобарный то определяю Q и L по соответствующим формулам:
по закону Гей-Люссака определяю конечный объем:

Q=M·C pm ·(T 2 -T 1)= 5,56·1022·400=2272928 (Дж);
L=P·(V 2 -V 1)=300000·2,15=645000 (Дж).
В цилиндре находится воздух при давлении Р=0,5 Мпа и температуре t 1 =400 0 C. От воздуха отнимается теплота при Р=const так, что в конце процесса устанавливается температура t 2 =0 0 C. Объем цилиндра, в котором находится воздух V 1 =400л.
Определить количество отнятой теплоты, конечный объем, изменеие внутренней энегии и совершенную работу сжатия C pm =1,028 
Так как процесс изобарный то по закону Гей-Люссака определяю конечный объем:

Согласно характеристическому уравнению Клайперона, определяю массу газа:
Из предыдущей задачи R=286,7 

Определяю количество теплоты которое выделяется:
Q=M·C pm ·(T 2 -T 1)=1,03·1028·(273-673)=-423536 (Дж);
Определяю количество затраченной работы:
L=P·(V 2 -V 1)= 500000·(0,16-0,4)=-120000 (Дж);
Из уравнения, по которому определяется полное количество, определяю изменение количества внутренней энергии:

Воздух, имеющий обьем V 1 =0,02 м3 при давлении Р 1 =1,1МПа и t 1 =25с расширяется в цилиндре с подвижным поршнем до давления Р 2 =0,11Мпа. Найти конечный обьем V 2 , конечную температуру t 2 , работу, произведенную воздухом, и подведенную теплоту, если расширение в цилиндре происходит:
б) адиабатно с показателем адиабаты к=1,4
в) политропно с показателем политропы n=1,3
P 1 /P 2 =V 2 /V 1
V 2 =0,02·1,1/0,11=0,2M 3
Q=L=RMT 1 Ln(V 2 /V 1)=P 1 V 1 Ln(V 2 /V 1)=1,1·10 6 ·0,02Ln(0,2/0,02)=22000Дж
V 1 /V 2 =(P 2 /P 1) 1/k
V 2 =V 1 /(P 2 /P 1) 1/k =0,02/(0,11/1,1) 1/1,4 =0,1036M 3
T 2 /T 1 =(P 2 /P 1) k-1/k
T 2 =(P 2 /P 1) k-1/k ·T 1 =(0,11/1,1) 1,4-1/1,4 ·298=20,32k
L=1/k-1(P 1 V 1 -P 2 V 2) =(1/1,4-1)· (1,1·10 6 ·0,02 -0,11·10 6 ·0,1)=2,0275·10 6 Дж
V 1 /V 2 =(P 2 /P 1) 1/n
V 2 =V 1 /(P 2 /P 1) 1/n =0,02/(0,11/1,1) 1/1,3 =0,118M 3
T 2 /T 1 =(P 2 /P 1) n-1/n
T 2 =(P 2 /P 1) n-1/n ·T 1 =(0,11/1,1) 1,3-1/1,3 ·298=175k
L= 1/n-1(P 1 V 1 -P 2 V 2)= (1/(1,3-1))· (1,1·10 6 ·0,02 -0,11·10 6 ·0,118)=30000Дж
1. «Энергия», Москва, 1975.
2. Литвин А.М. «Теоретические основы теплотехники», издательство «Энергия», Москва,1969.
3. Тугунов П.И., Самсонов А.А., «Основы теплотехники, тепловые двигатели и паросиловое хозяйство», издательство «Недра», Москва, 1970.
4. Крутов В.И., «Теплотехника», издательство «Машиностроение», Москва, 1986.
Видео:Объемная доля компонента газовой смесиСкачать

Газовые смеси
Читайте также:
|



















 (3.1)
(3.1) (3.2)
(3.2) ,
,  (3.3)
(3.3) ,
,  (3.4)
(3.4) ,
,  (3.5)
(3.5)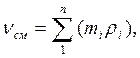
 (3.7)
(3.7) (3.8)
(3.8)
 (3.9)
(3.9)
 (3.10)
(3.10)






m.jpg)
m.jpg)
m.jpg)

m.jpg)
m.jpg)
m(2).jpg)
_m.jpg)


m.jpg)
_m.jpg)


_01.jpg)
_02.jpg)
_03.jpg)
_04.jpg)
_1.jpg)
_2.jpg)
_3.jpg)
_4.jpg)
_5.jpg)
_6.jpg)

















