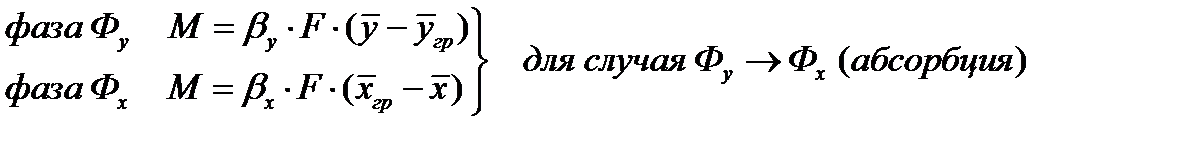Уравнение массопередачи при переменной движущей силе процесса

В связи со сложностью механизма массоотдачи в практических расчетах используют относительно простое уравнение массоотдачи:

Т.е. скорость массоотдачи (кг/с) пропорциональна межфазной поверхности и средней разности концентраций на этой поверхности и в ядре фазы.

— средние концентрации в ядре фаз;

— концентрации на межфазной повер

— коэффициенты массоотдачи в фазах .

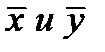
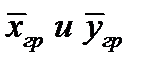
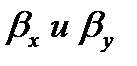
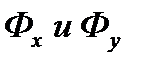
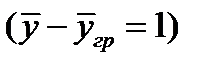
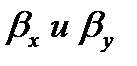
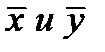
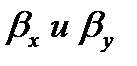
Коэффициент массоотдачи равен количеству вещества, отдаваемого межфазной поверхности в фазу за 1сек. при единичной движущей силе . Размерность зависит от размерностей М, . Например, [β] = [кг/м 2 ∙с∙(единица движущей силы)]. — функции многих переменных (ρ, ν, Re, Г₁, Г₂, Г₃…).

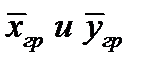
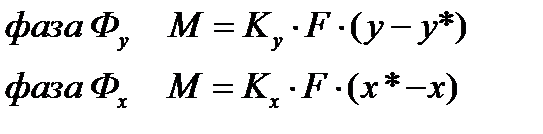
Т.к практически измерить невозможно, в основное уравнение массопередачи вместо этих концентраций вводят равновесные концентрации x * и y * :

,

где y * и x * — равновесные концентрации в данной фазе, соответствующие концентрациям в ядре другой фазы; K_y и K_x – коэффициенты массопередачи, соответствующие концентрациям распределяемого вещества в фазах .

Т.е. движущая сила процесса массопереноса, выражающая отклонение системы от равновесия, равна разности рабочей и равновесной концентраций вещества в данной фазе. Размерности коэффициентов массоотдачи и массопередачи одинаковы.

Движущая сила массопереноса – величина переменная, т.к. концентрации изменяются вдоль межфазной поверхности. Поэтому пользуются средней движущей силой:

— основное уравнение массопередачи.

Из основного уравнения массопередачи обычно определяют F.

Пусть линия равновесия описывается уравнением y * = m∙x, где m – тангенс угла наклона равновесной линии. Тогда коэффициенты массопередачи и массоотдачи связаны уравнениями аддитивности фазовых сопротивлений:

— для фазы Ф_у.

— для фазы Ф_х, где — сопротивление массопередаче; — сопротивление массоотдачи в фазах. .

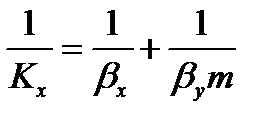
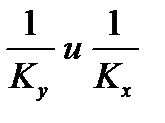
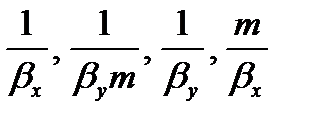
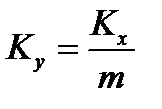
Для кривой линии равновесия m, K_x, K_y изменяются по высоте аппарата. В этом случае используют К_ср.

Иногда сопротивление одной из фаз очень мало, и тогда .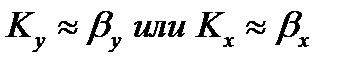

Повысить скорость массопередачи можно увеличением скорости потока той фазы, сопротивление которой больше.

Аддитивность фазовых сопротивлений нарушается при значительном сопротивлении межфазной поверхности.

Основное уравнение массопередачи аналогично основному уравнению теплопередачи: .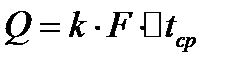

Видео:Массообменные процессы. Часть 1. Уровень: начальныйСкачать

Основное уравнение массопередачи

Массообменные процессы

В химической технологии многие процессы связаны с переходом вещества из одной фазы в другую. Такие процессы называются массообменными. Эти процессы еще называются диффузионными, поскольку такой переход обусловлен скоростью диффузии вещества.

К массообменным процессам в химической технологии относятся:

Абсорбция и адсорбция – это сорбционные процессы, связанные с разделением газовых и парогазовых смесей путем избирательного поглощения одного или нескольких компонентов. В случае абсорбции – поглотитель – жидкость. В случае адсорбции – твердый поглотитель. В случае абсорбции происходит массообмен между газом и жидкостью; в случае адсорбции – между газом и твердым телом.

Ректификация – процесс разделения жидких смесей, состоящих из нескольких компонентов, обладающих различной упругостью паров, основанный на многократном противоточном взаимодействии жидкости и пара. При ректификации происходит массо — и теплообмен между паровой и жидкой фазами.

Экстракция — процесс разделения смеси компонентов, входящих в состав твердой или жидкой фаз, путем обработки их жидким растворителем, способным полностью или частично извлекать один из компонентов. В данном случае массообмен происходит между твердой и жидкой фазами (экстракция из твердого тела) или между жидкими фазами (жидкостная экстракция).

Кристаллизация и растворение твердых веществ. При кристаллизации происходит массообмен в направлении от жидкого раствора к твердому телу – кристаллу, а при растворении – от твердого тела к жидкости (раствору).

Сушка – процесс удаления влаги из влажных материалов за счет подводимой извне тепловой энергии. При сушке происходит массопередача влаги из влажного материала в окружающую газовую среду.

Фазовое равновесие

Переход вещества из одной фазы в другую в направлении достижения равновесия называется массопередачей.

Под равновесием понимается такое состояние между фазами, когда в единицу времени из первой фазы во вторую переходят столько же молекул вещества, сколько из второй в первую.

Правило фаз. Существование данной фазы в равновесии с другими возможно лишь при вполне определенных условиях и определяется правилом фаз. Эти условия (температура, концентрация), при которых система находится в равновесии, могут меняться.

Будем называть компонентом системы каждое из находящихся в ней химических однородных веществ, которое выделяется из нее и может существовать самостоятельно длительное время. Компоненты системы, наименьшее число которых достаточно для образования всех фаз данной системы, называется независимыми компонентами.

Для процесса массопередачи на равновесие системы влияют только 2 внешних фактора – температура и давление, и правило фаз записывается следующим образом: C = K – Ф + 2,

С – число степеней свободы или минимальное число факторов, которые можно изменять независимо друг от друга без нарушения равновесия системы.

Ф – число фаз системы;K – число независимых компонентов системы.

В зависимости от числа степеней свободы, системы могут быть:

1 безвариантными – С=0;

2 одновариантными С=1;

3 двухвариантными С=2 ;

4 многовариантными С >2.

Для систем, состоящих из 2 или более числа компонентов, их состояние и равновесие зависят от температуры, Р и количественного состава фаз.

Двухкомпонентная система, состоит из двух фаз, имеет две степени свободы (С=2 – 2 + 2 = 2), т.е. для нее без нарушения равновесия фаз можно менять одновременно t-ру и Р. В том случае, если один из этих факторов принять постоянным (t-ру или Р), то состояние равновесия между фазами будет характеризоваться лишь величиной другого переменного фактора и составом фаз. Так, например, при Р=const каждой температуре будет соответствовать строго определенный состав фаз.

Закон Генри

Равновесный состав фаз в системах газ-жидкость характеризуется равновесным распределением растворимого газа между инертным газом и растворяющей жидкостью и определяется для идеальных газов по закону Генри.

,

где: р– парциальное давление газа над раствором; х – молярная доля газа в растворе; Е – константа Генри (имеет размерность давления). Закон Генри формулируется следующим образом:

Парциальное давление растворенного идеального газа пропорционально его молярной доле в растворе, или

растворимость идеального газа в жидкости при данной t-ре пропорциональна его парциальному давлению над раствором.

(*)

Если у* — молярное равновесное содержание растворимого газа в газовой смеси и Р – общее давление газа, то парциальное давление р будет равно:

, подставим в (*), получим

, откуда ,

где m – коэффициент распределения или константа фазового равновесия (безразмерная величина).

Фазовое равновесие между раствором идеального газа в жидкости и газовой смесью над ней подчиняется закону Генри только при t > t критических (для газа).

Поскольку при сильном разбавлении любой раствор приближается к идеальным, то закон Генри применим и к разбавленным растворам, при этом он работает тем точнее, чем выше разбавление.

По этой же причине закон Генри достаточно точно описывает равновесие для плохо растворимых газов.

Для газов со сравнительно высокой растворимостью закон Генри справедлив лишь при низких концентрациях; при высоких концентрациях растворимость ниже, чем это следует из закона Генри.

Закон Рауля. При температурах газа ниже критической система будет двухфазной: жидкость – насыщенный пар.

Равновесие в этом случае характеризуется составом жидкости х и составом находящегося в равновесии с жидкостью пара у*.

Равновесие фаз для жидких идеальных растворов описывается законом Рауля: – парциальное давление любого компонента в парах над смесью жидкостей равно упругости насыщенного пара этого компонента (при данной температуре) умноженной на его молярную долю в жидкости.

,

p_a– парциальное давление пара компонента а над смесью жидкостей;

Р_a – давление насыщенного пара компонента а при t — ре смеси,

х – молярная доля компонента а в жидкой смеси.

Для любого компонента его парциальное давление можно определить:

и следовательно равновесный состав пара над жидкостью:

;

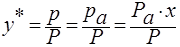
Р – общее давление паров над жидкой смесью.

Основное уравнение массопередачи

В массообменных процессах вещество путем диффузии переходит из одной фазы в другую, причем компонент, который переходит называется распределяемым веществом.

Основной характеристикой массообменных процессов является скорость массопередачи, которая представляет собой количество распределяемого вещества М(кг), переходящего из одной фазы в другую через единицу поверхности соприкосновения фаз F(м ²) в единицу времени , т.е.

.

Скорость процесса массопередачи пропорциональна его движущей силе, которая равна разности концентраций

, где у– концентрация распределяемого вещества в первой фазе, откуда вещество уходит;

у * — концентрация распределяемого вещества у поверхности раздела фаз (со стороны первой фазы), при которой бы существовало равновесие с концентрацией второй фазы х.

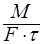
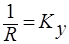
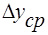
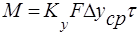
Т.о. скорость массопередачи = ; R-диффузионное сопротивление переносу вещества. — коэффициент массопередачи. Т.к. концентрации фаз в ходе процесса меняются, то изменяется и . Поэтому вводится понятие средней движущей силы .

— основное уравнение массопередачи, где М-нагрузка аппарата. В условиях стационарного процесса .

Из основного уравнения массопередачи: — Коэффициент массопередачи– это количество вещества, переданного из одной фазы в другую через единицу поверхности в единицу времени при движущей силе равной единице.

Движущая сила одного и того массообменного процесса может быть выражена разностью концентраций и по другой фазе:

, которая будет иметь другую численную величину. Основное уравнение массопередачи в данном случае: ,

— коэффициент массопередачи, отнесенный ко 2 фазе. Он имеет другое численное значение, но тот же физический смысл. Следовательно, можно записать (поскольку слева одно и тоже значение М): , отсюда .

Чаще всего в массообменных аппаратах поверхность соприкасающихся фаз практически неопределима (например: жидкость с газовыми пузырями). Поэтому основное уравнение массопередачи (ОУМП) применяют в виде

, , где V-рабочий объём аппарата;

— объёмные коэффициенты массопередачи.

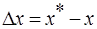
Объёмные коэффициенты массопередачи – представляют собой количество вещества переданного из одной фазы в другую в единице рабочего объёма аппарата в единицу времени при движущей силе=1.

Из основного уравнения массопередачи определяется поверхность массопередачи или объём рабочей зоны аппарата .

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Лекция № 11 Процесс массопередачи

Массопередача – это сложный процесс, включающий перенос вещества (массы) в пределах одной фазы, перенос через поверхность раздела фаз и его перенос в пределах другой фазы. Как известно, при теплопередаче обменивающиеся теплотой среды в большинстве случаев разделены твердой стенкой, в то время как массопередача происходит обычно через границу раздела соприкасающихся фаз. Эта граница может быть либо подвижной (массопередача в системах газ-жидкость или пар-жидкость, жидкость-жидкость), либо неподвижной (массопередача с твердой фазой).

массоотдача – это перенос вещества из фазы к границе раздела фаз или в обратном направлении, т. е. в пределах только одной фазы.

Виды процессов массопередачи. В промышленности применяются в основном следующие процессы массопередачи:

1. Абсорбция — поглощение газа жидкостью, т. е. процесс разделения, характеризуемый переходом вещества из газовой фазы в жидкую.

2. Экстракция (в системе жидкость-жидкость) — извлечение вещества, растворенного в жидкости, другой жидкостью, практически несмешивающейся или частично смешивающейся с первой. При этом извлекаемый компонент исходного раствора переходит из одной жидкой фазы в другую.

8. Перегонка — разделение гомогенных жидких смесей путем взаимного обмена компонентами между жидкостью и паром, полученным испарением разделяемой жидкой смеси.

4. Адсорбция — поглощение компонента газа, пара или раствора твердым пористым поглотителем, т. е. процесс разделения, характеризуемый переходом вещества из газовой (паровой) или жидкой фазы в твердую.

5. Сушка — удаление влаги из твердых материалов, главным образом путем ее испарения.

6. Кристаллизация — выделение твердой фазы в виде кристаллов из растворов или расплавов.

7. Растворение и экстракция (в системе твердое тело — жидкость).

Процессы массопередачи можно разделить на две группы.

К одной группе относятся процессы (абсорбция, экстракция и др.), в которых участвуют минимально три вещества: одно находится только в одной фазе, другое — только во второй фазе, а третье — переходит из одной фазы в другую и представляет собой распределяемое между фазами вещество.

К другой группе относятся процессы (например, перегонка), в которых вещества, составляющие две фазы, обмениваясь компонентами, сами непосредственно участвуют в массопередаче и уже не могут рассматриваться как инертные носители распределяемого вещества.

Скорость массообменных процессов, как правило, лимитируется молекулярной диффузией. Поэтому процессы массопередачи иногда называют диффузионными процессами.

Равновесие при массопередаче

Правило фаз. Знание равновесия в процессах массопередачи позволяет установить пределы, до которых могут протекать эти процессы. В основе равновесия лежит известное правило фаз:

Видео:Лекция 2 МассопередачаСкачать

Ф + С = К + 2, (1)

где Ф — число фаз; С — число степеней свободы, т. е. число независимых переменных, значения которых можно произвольно изменять без нарушения числа или вида (состава) фаз в системе; К — число компонентов системы.

Правило фаз указывает число параметров, которое можно менять произвольно (в известных пределах) при расчете равновесия в процессах масообмена.

Зависимости между независимыми переменными могут быть изображены в плоских координатах в виде так называемых фазовых диаграмм. В расчетах по массопередаче используют диаграммы зависимости давления от концентрации (при t = const), температуры от концентрации (при Р = const) и диаграммы зависимости между равновесными концентрациями фаз, приведенные ниже.

Фазовое равновесие. Линия равновесия. Рассмотрим в качестве примера процесс массопередачи, в котором аммиак, представляющий собой распределяемый компонент, поглощается из его смеси с воздухом чистой водой, т. е. ввиду отсутствия равновесия переходит из газовой фазы Фу, где его концентрация равна у, в жидкую фазу Фх, имеющую начальную концентрацию х = 0. С началом растворения аммиака в воде начнется переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде и на границе раздела фаз. С течением времени скорость перехода аммиака в воду будет снижаться, а скорость обратного перехода возрастать, причем такой двусторонний переход будет продолжаться до тех пор, пока скорости переноса в обоих направлениях не станут равны друг другу. При равенстве скоростей установится динамическое равновесие, при котором не будет происходить видимого перехода вещества из фазы в фазу.

При равновесии достигается определенная зависимость между предельными или равновесными концентрациями распределяемого вещества в фазах для данных температуры и давления, при которых осуществляется процесс массопередачи.

В условиях равновесия некоторому значению отвечает строго определенная равновесная концентрация в другой фазе, которую обозначим через . Соответственно концентрация у отвечает равновесная концентрация . В самом общем виде связь между концентрациями распределяемого вещества в фазах при равновесии выражается зависимостью:

или . (2)

Любая из этих зависимостей изображается графически линией равновесия, которая либо является кривой, как показано на рис. 1, либо в частном случае — прямой линией. На рис. 1, а показана равновесная кривая для системы с компонентами-носителями, выражающая зависимость равновесной концентрации, например в газовой фазе, от концентрации жидкой фазы при Р = const и t = const. На рис. 1, б приведен пример равновесной кривой для процесса ректификации, построенной при Р = const. Каждая точка кривой, как показано на рисунке, соответствует разным температурам (t1, t2 и т. д.).

Отношение концентраций фаз при равновесии называется коэффициентом распределения . Для разбавленных растворов линия равновесия близка к прямой, и т является практически величиной постоянной, равной тангенсу угла наклона линии равновесия.

Конкретный вид законов равновесного распределения различен для разных процессов массопередачи. Так, например, в процессе абсорбции при низких концентрациях распределяемого вещества в исходном растворе равновесие описывается законом Генри для идеальных растворов в процессах ректификации — законом Рауля и т. д.

Зная линию равновесия для конкретного процесса и рабочие, т. е. неравновесные, концентрации фаз в соответствующих точках, можно определить направление и движущую силу массопередачи в любой точке аппарата. На основе этих данных может быть рассчитана средняя движущая сила, а по ней — скорость процесса массопередачи.

Материальный баланс. Рабочая линия. Рабочие концентрации распределяемого вещества не равны равновесным, и в действующих аппаратах никогда не достигают равновесных значений.

Зависимость между рабочими концентрациями распределяемого вещества в фазах изображается линией, которая носит название рабочей линии процесса. Вид функции или уравнение рабочей линии в его общем виде, является одинаковым для всех массообменных процессов и получается из их материальных балансов.

Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз (рис. 2). Пусть в процессе массопередачи из фазы в фазу, например из газовой фазы в жидкую, переходит только один распределяемый компонент (скажем, аммиак).

Сверху в аппарат поступает Lн кг/с одной фазы (жидкой), содержащей вес. долей распределяемого компонента, а снизу из аппарата удаляется Lк кг/с той же фазы, содержащей вес. долей распределяемого компонента. Снизу в аппарат поступает кг/с другой фазы (газовой) концентрацией и сверху удаляется кг/с этой фазы, имеющей концентрацию вес. долей распределяемого компонента.

Тогда материальный баланс по всему веществу

, (3)

и материальный баланс по распределяемому компоненту

. (4)

Теперь напишем уравнения материального баланса для части аппарата от его нижнего конца до некоторого произвольного сечения, для которого расходы фаз составляют G и L кг/с, а их текущие концентрации равны и соответственно.

Материальный баланс по всему веществу

, (5)

и материальный баланс по распределяемому компоненту

. (6)

Решая это уравнение относительно , получим

. (7)

Уравнение (7) представляет собой уравнение рабочей линии, выражающее связь между рабочими концентрациями распределяемого компонента в фазах для произвольного сечения аппарата.

Расходы фаз постоянны по высоте аппарата, например в процессах ректификации, когда числа молей компонентов, которыми обмениваются фазы, равны. В других случаях, если концентрации фаз мало изменяются по высоте аппарата, то расходы фаз по его высоте можно с достаточной для практических целей точностью считать постоянными, т. е. принять L = const и G = const. При этом Lк = L, Gн = G и уравнение (7) приводится к виду

. (8)

Вводя обозначения и , находим

. (9)

Выражения (8) и (9) являются уравнениями рабочей линии, которыми обычно пользуются при расчетах массообменных процессов.

Таким образом, рабочая линия представляет собой прямую, которая наклонена к горизонту под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В. Рабочая линия для всего аппарата ограничена точками с координатами и (верхний конец аппарата, рис. 3) и и (нижний конец аппарата).

Скорость массопередачи

Скорость массопередачи связана с механизмом переноса распределяемого вещества в фазах между которыми происходит массообмен.

Перенос вещества внутри фазы может происходить только путем молекулярной диффузии либо путем конвекции и молекулярной диффузии одновременно. Посредством одной молекулярной диффузии вещество перемещается, строго говоря, лишь в неподвижной среде. В движущейся среде перенос вещества осуществляется как молекулярной диффузией, так и самой средой в направлении ее движения или отдельными ее частицами в разнообразных направлениях.

В турбулентном потоке перенос молекулярной диффузией преобладает только вблизи границы фазы. При турбулентном течении возникают нерегулярные пульсации скорости, под действием которых, наряду с общим движением потока, происходит перемещение частиц во всех направлениях, в том числе и в поперечном.

Конвективный перенос вещества, осуществляемый под действием турбулентных пульсаций, часто называют турбулентной диффузией.

Молекулярная диффузия. Молекулярной диффузией называется перенос распределяемого вещества, обусловленный беспорядочным тепловым движением молекул, атомов, ионов, коллоидных частиц. Молекулярная диффузия описывается первым законом Ф и к а, согласно которому масса вещества dМ, продиффундировавшего за время dt через элементарную поверхность dF (нормальную к направлению диффузии), пропорциональна градиенту концентрации этого вещества

или . (1)

Из выражения (1) следует, что удельный поток вещества, переносимого молекулярной диффузией через единицу поверхности (F = 1) в. единицу времени (t = 1), или скорость молекулярной диффузии, составляет

. (2)

По своей структуре закон Фика аналогичен закону Фурье, описывающему передачу тепла теплопроводностью, причем аналогом градиента температур является в данном случае градиент концентраций, представляющий собой изменение концентрации диффундирующего вещества на единицу длины нормали между двумя поверхностями постоянных, но различных концентраций.

Коэффициент пропорциональности D в выражении закона Фика называется коэффициентом молекулярной диффузии, или просто коэффициентом диффузии. Знак минус перед правой частью первого закона Фика указывает на то, что молекулярная диффузия всегда протекает в направлении уменьшения концентрации распределяемого компонента.

Согласно уравнению (1), коэффициент диффузии выражается как:

откуда (до сокращения одноименных величин) вытекает физический смысл D. Коэффициент диффузии, показывает, какая масса вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

Коэффициент молекулярной диффузии представляет собой физическую константу, характеризующую способность данного вещества проникать вследствие диффузии в неподвижную среду. Величина D таким образом не зависит от гидродинамических условий, в которых протекает процесс.

Турбулентная диффузия. Масса вещества dMт, переносимого в пределах фазы вследствие турбулентной диффузии, может быть принята, по аналогии с молекулярной диффузией, пропорциональной поверхности dF, времени dt и градиенту концентрации и определяется по, уравнению

, (3)

где — коэффициент турбулентной диффузии.

Коэффициент турбулентной диффузии показывает какая масса вещества передается посредством турбулентной диффузии в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

Коэффициент выражается в тех же единицах, что и коэффициент молекулярной диффузии D, т. е. в м2/с. Однако в отличие от D коэффициент турбулентной диффузии не является физической константой; он зависит от гидродинамических условий, определяемых в основном скоростью потока и масштабом турбулентности.

Конвективный перенос. Скорость конвективного, переноса вещества вместе с самой средой в направлении, совпадающем с направлением общего потока, равна

, (4)

где v — скорость потока жидкости, газа или пара; С — коэффициент пропорциональности.

Суммарный перенос вещества вследствие конвективного переноса и молекулярной диффузии, по аналогии с теплообменом, называют конвективным массообменом или конвективной диффузией.

Распределение концентрации при переносе путем конвективной диффузии определяется в самом общем виде дифференциальным уравнением конвективной диффузии.

Дифференциальное уравнение конвективной диффузии. Выделим в потоке данной фазы элементарный параллелепипед с ребрами dx, dy и dz, ориентированными относительно осей координат, как показано на рис. 1. Рассмотрим материальный баланс по распределяемому веществу для параллелепипеда в наиболее общем случае неустановившегося массообмена. Будем считать, что процесс переноса происходит в условиях установившегося движения потока фазы. Распределяемое вещество проходит сквозь грани параллелепипеда как путем конвективного переноса, так и молекулярной диффузии.

Обозначим концентрацию распределяемого вещества в плоскости левей грани параллелепипеда площадью dydz через с и проекции скорости на оси координат для данного элемента (точки) потока — через , и , соответственно.

Тогда масса вещества, поступающего только путем конвективной диффузии через площадь dydz, т. е. в направлении оси х, за время dt составит

. (5)

На противоположной грани параллелепипеда скорость в направлении оси х равна и концентрация распределяемого вещества составляет . Следовательно, за время dt через противоположную грань параллелепипеда выходит путем конвективной диффузии:

. (6)

Разность между массами вещества, прошедшего через противоположные грани параллелепипеда за время dt в направлении оси х, равна

, (7)

где dV = dx dy dz — объем элементарного параллелепипеда. Аналогично в направлении осей у и z:

и . (8)

Таким образом, содержание распределяемого вещества в объеме параллелепипеда изменится за время dt вследствие перемещения вещества только путем конвективной диффузии на величину

или в развернутом виде

. (9)

Согласно уравнению неразрывности потока для установившегося движения фазы

. (10)

Следовательно, предыдущее выражение dMк примет вид

. (11)

Масса распределяемого вещества, поступающего в параллелепипед только путем молекулярной диффузии через грань dy dz за время dt составляет

. (12)

Масса вещества, выходящего за то же время путем молекулярной диффузии через противоположную грань,

. (13)

Разность между массами продиффундировавшего через противоположные грани параллелепипеда вещества в направлении оси х за время dt равна

. (14)

Аналогично в направлении осей у и z:

и . (15)

Масса распределяемого вещества в объеме всего параллелепипеда за время dt изменится при переносе путем молекулярной диффузии на величину

. (16)

В результате изменение массы распределяемого вещества во времени в объеме параллелепипеда

. (17)

Изменение массы распределяемого вещества за счет конвективной и молекулярной диффузии в объеме параллелепипеда по закону сохранения массы должно равняться соответствующему изменению массы этого вещества во времени, т. е.

. (19)

Проводя соответствующие сокращения и перегруппировывая члены этого уравнения, получим

(20)

или в более краткой записи

. (20, а)

Уравнение (20) представляет собой дифференциальное уравнение конвективной диффузии. Оно выражает закон распределения концентрации данного компонента в движущейся стационарно среде при неустановившемся процессе массообмена.

Уравнение (20) по структуре аналогично дифференциальному уравнению конвективного теплообмена (уравнению Фурье-Кирхгофа). Отличие состоит в том, что в уравнение (20) вместо температурного градиента входит градиент концентрации, а вместо коэффициента температуропроводности а — коэффициент молекулярной диффузии D.

Для частного случая установившегося массообмена уравнение (20) принимает вид:

. (21)

При массообмене в неподвижной среде = = = 0, а конвективная составляющая в левой части уравнения (19) равна нулю, и уравнение обращается в дифференциальное уравнение молекулярной диффузии.

. (22)

Уравнение (22) носит название второго закона Фика. В дифференциальном уравнении конвективной диффузии, помимо концентрации, переменной является скорость потока. Поэтому данное уравнение надо рассматривать совместно с дифференциальными уравнениями гидродинамики: уравнениями Навье-Стокса и уравнением неразрывности потока. Однако эта система уравнений не имеет аналитического решения, и для получения расчетных зависимостей по массообмену приходится прибегать к преобразованию дифференциального уравнения конвективной диффузии методами теории подобия.

Ввиду сложности механизма процессов массоотдачи в фазах для практических целей принимают, что скорость массоотдачи пропорциональна движущей силе, равной разности концентраций в ядре и на границе фазы или (в случае обратного направления переноса) разности концентраций на границе и в ядре фазы. Соответственно, если распределяемое вещество переходит из фазы Фу в фазу Фх, то основное уравнение массоотдачи, определяющее количеством М вещества, переносимого в единицу времени в каждой из фаз (к границе фазы или в обратном направлении), выражается следующим образом:

(1)

, (1, а)

входящие в эти уравнения разности концентраций и представляют собой движущую силу процесса массоотдачи соответственно в фазах Фу и Фх, причем и — средние концентрации в основной массе (ядре) каждой из фаз, и — концентрации у границы соответствующей фазы.

Коэффициенты пропорциональности в уравнениях (1) и (1, а) называются коэффициентами массоотдачи. Коэффициенты массоотдачи (в фазе Фх и (в фазе Фу) показывают, какая масса вещества переходит от поверхности раздела фаз в ядро фазы: или в обратном направлении) через единицу поверхности в единицу времени при движущейся силе, равной единице.

Коэффициент массоотдачи является не физической константой, а кинетической характеристикой, зависящей от физических свойств фазы (плотности, вязкости и др.) и гидродинамических условий в ней (ламинарный или турбулентный режим течения), связанных в свою очередь с физическими свойствами фазы, а также с геометрическими факторами, определяемыми конструкцией и размерами массообменного аппарата, Таким образом, величина является функцией многих переменных, что значительно осложняет расчет или опытное определение коэффициентов массоотдачи. Значениями последних учитывается как молекулярный, так и конвективный перенос вещества в фазе.

По своему смыслу коэффициент массоотдачи является аналогом коэффициента теплоотдачи в процессах переноса тепла, а основное уравнение массоотдачи идентично по структуре основному уравнению теплоотдачи.

Коэффициент массоотдачи может быть выражен в различных единицах в зависимости от выбора единиц для массы распределяемого вещества и движущей силы. Если принять, что масса вещества выражена в килограммах, то в общей форме коэффициент массоотдачи выразится следующим образом:

При этом единица измерения р в каждом конкретном случае будет связана с единицами, принятыми для выражения движущей силы (табл. Х-1).

Подобие процессов переноса массы. Наиболее строгий и принципиально возможный путь для определения коэффициентов массоотдачи, заключается в интегрировании уравнения диффузии в движущейся среде (Х,19) совместно с уравнениями движения, т. е. с уравнениями Навье-Стокса и уравнением неразрывности потока при заданных начальных и граничных условиях.

Однако система указанных уравнений практически не имеет общего решения. Поэтому так же, как для гидродинамических и теплообменных процессов, не решая системы основных уравнений, можно методами теории подобия найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде обобщенного (критериального) уравнения массоотдачи.

Общая функциональная зависимость Nu’ от определяющих критериев и симплексов подобия для неустановившихся процессов массоотдачи может быть выражена как

. (13)

Для установившихся процессов массоотдачи условие равенства критериев Fo’ в сходственных точках подобных потоков отпадает н приведенные выше обобщенные зависимости принимают вид:

. (14)

Расчетная зависимость типа уравнения (13 и 14) называется обобщенным или критериальным уравнением массоотдачи.

Как отмечалось, процесс массопередачи включает процессы массоотдачи в пределах каждой из двух взаимодействующих фаз и, кроме того, процесс переноса распределяемого вещества через поверхность раздела фаз. Сложность расчета процесса связана с тем, что практически невозможно измерить концентрации фаз непосредственно у границы их раздела. Учитывая это, основное уравнение массопередачи, определяющее массу М вещества, переносимого из фазы в фазу в единицу времени (нагрузку аппарата), выражают следующим образом:

, (1)

, (2)

где у*, х* — равновесные концентрации в данной фазе, соответствующие концентрациям распределяемого вещества в основной массе (ядре) другой фазы; Ку, Кх— коэффициенты и массопередачи, выраженные соответственно через концентрации фаз Фу и Фх.

Коэффициент массопередачи (Kу или Кх) показывает, какая масса вещества переходит из фазы в фазу за единицу времени через единицу поверхности контакта фаз при движущей силе массопередачи, равной единице.

По физическому смыслу коэффициенты массопередачи отличаются от коэффициентов массоотдачи, но выражены в одинаковых с ними единицах измерения. Таким образом, коэффициенты массопередачи могут выражаться в м/с, кг/(м2 с); кг/(м2 с мол доли) и в с/м.

Концентрации фаз изменяются при их движении вдоль поверхности раздела, соответственно изменяется движущая сила массопередачи. Поэтому в уравнение массопередачи вводят величину средней движущей силы ( или ). Тогда уравнения (1) и (2) принимают вид:

, (3)

. (4)

С помощью уравнений (3) и (4) обычно находят поверхность контакта фаз F и по ней рассчитывают основные размеры аппарата. Для определения F необходимо предварительно рассчитать коэффициент массопередачи Kу или Кх и среднюю движущую силу. Величина М либо задается при расчете, либо определяется из материального баланса.

Зависимость между коэффициентами массопередачи и массоотдачи. Чтобы установить связь между коэффициентом массопередачи и коэффициентами массоотдачи, обычно принимают, что да границе раздела фаз см. рис. 5) достигается равновесие. Это предположение равносильно допущению о том, что сопротивлением переносу через границу раздела фаз можно пренебречь. Отсюда вытекает, как следствие, положение об аддитивности фазовых сопротивлений, которое является одной из предпосылок для расчета коэффициента массопередачи. Допустим, что распределяемое вещество переходит из фазы Фу в фазу Фх, и движущая сила массопередачи выражается в концентрациях фазы Фу. При установившемся процессе массопередачи количество вещества, переходящее из фазы в фазу, определим по уравнению (1).

Для упрощения рассмотрим случай, когда равновесная зависимость % между концентрациями в фазах линейна, т. е. линия равновесия описывается уравнением у* = m x, где т – тангенс угла наклона линии равновесия. После ряда преобразований получаем

(9)

При выражении коэффициента массопередачи в концентрациях фазы Фх аналогичные рассуждения приводят к зависимости

, (10)

Левые части уравнений (9) и (10) представляют собой общее сопротивление переносу вещества из фазы в фазу, т. е. сопротивление массопередаче, а их правые части — сумму сопротивлений массоотдаче в фазах. Поэтому зависимости (9) и (10) являются уравнениями аддитивности фазовых сопротивлений.

При т = const уравнение (10) можно получить, разделив уравнение (9) на т. Отсюда следует, что величины Kу и Kх связаны зависимостью Kу = Kх/m.

Уравнения аддитивности (9) и (10) выведены для линейной равновесной зависимости, но они остаются в силе и для кривой линии равновесия.

🎬 Видео

Практическое занятие по расчёту абсорбцииСкачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Уравнение Мещерского, формула ЦиолковскогоСкачать

Основы массорепедачи. Первая лекцияСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать

Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Уравнение с модулемСкачать

Закон БернуллиСкачать

Подобие процессов конвективного теплообменаСкачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать

Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

Гидромеханические процессы. Часть 1. Уровень: начальный.Скачать

Теоретическая механика. Элементы аналитической механики.Скачать