Уравнение маргулиса для бинарной смеси

Видео:Квартирник у Маргулиса: Машина ВремениСкачать

Разделение жидких растворов

Законы Гиббса-Коновалова устанавливают связь между составом жидкого раствора и составом насыщенного равновесного с ним пара в зависимости от температуры и давления.В равновесной двухкомпонентной системе сумма мольных долей компонентов в жидкой и паровой фазах равны единице:

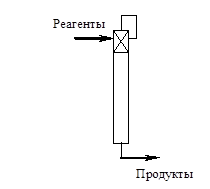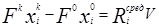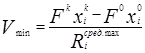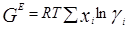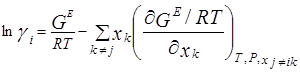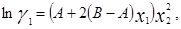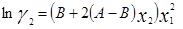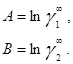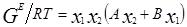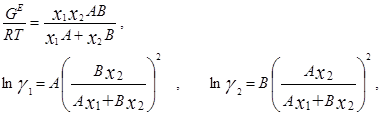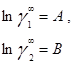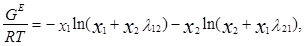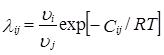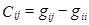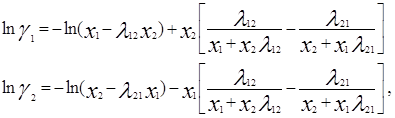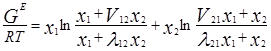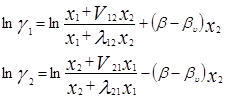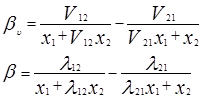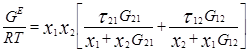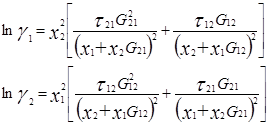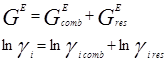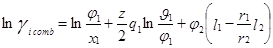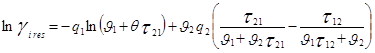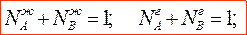
Законы Гиббса-Коновалова и предыдущее уравнение справедливы для двухкомпонентных смесей, состоящих из летучих компонентов.Равновесие между раствором и паром удобно рассма-тривать в виде диаграмм, выражающих зависимость температуры жидкой смеси от ее состава.

В условиях равновесия относительное содержание компонента в паровой фазе отличается от содержания этого компонента в жидком растворе.В паре содержание больше того компонента, добавление которого в раствор понижает температуру кипения или повышает давление насыщенных паров.Пар обогащается более летучим компонентом.При постоянном давлении температура кипения раствора возрастает при увеличении концентрации компонента, содержание которого в паре меньше, чем в растворе.При постоянной температуре давление пара над раствором при увеличении концентрации компонента, содержание которого в паре больше, чем в растворе.

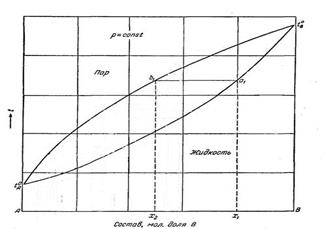
Диаграммы состава «жидкость-пар» двухкомпонент-ной системы при постоянном давлении (а) и постоянной температуре (б).
I-паровая фаза; II -пар+жидкость; III — жидкая фаза.

Точки экстремума на кривых температуры кипения (P=const) или на кривых давления (T=const) соответствуют растворам, состав которых одинаков с составом равновесного с ней пара. Нераздельнокипящие смеси называют азеотропными смесями.В условиях равновесия азеотропные смеси испаряются как чистое вещество.В азетропных смесях в точках экстремума

Законы Гиббса-Коновалова справедливы вдали от критического состояния двухфазной системы.

Диаграммы состава «жидкость-пар» двухкомпонент-ной системы с азеотропными точками при постоянном давлении (а) и постоянной температуре (б).
I-паровая фаза; II -пар+жидкость; III — жидкая фаза.

Термодинамическое обоснование законов Гиббса-Коновалова

Отношение между долями компонентов в паровой и жидкой фазах выражается следующим уравнением:

Уравнение показывает изменение состава жидкости и пара в соответствити с закономами Гиббса-Коновалова.К термодинамическому обоснованию законов Гиббса-Коновалова можно подойти, используя уравнение Дюгема-Маргулиса.

Уравнение Дюгема-Маргулиса позволяет определить связь между изменением парциального давления компонентов (рА, рВ) и составвом раствора (NAЖ). С его помощью можно рассчитать давление пара одного из компонентов раствора, если известны давление пара другого компонента и состав раствора.Уравнение Дюгема-Маргулиса справедливо для любого неидеального двухкомпонентного жидкого раствора, образованного летучими компонентами.Уравнение Дюгема-Маргулиса позволяет определить изменение общего давления системы в зависимости от мольной доли более летучего компонента, которое равно:

Перегонка (дистилляция) и ректификация

Соотношение между жидкой и паровой фазами в гетерогенной области II диаграммы состава двухкомпонентной системы находят по правилу рычага.

Отрезки на прямой, соединяющей на диаграмме состава двухкомпонентной системы паровую и жидкую фазы, отсекаемые определенной точкой на этой прямой, обратно пропорционально числу молей каждой из фаз. при температуре tкип правило рычага записывается следующим образом:

Дистилляцией или дробной перегонкой называют разделение жидких растворов, основанное на отличии состава жидкости от состава образующегося из нее пара.Дистилляция осуществляется путем частичного испарения и последующей конденсации пара.Отгонная фракция (дистиллят) обогащена более летучим (низкокипящим) компонентом, а неотогнанная жидкость (кубовой остаток, конденсат) обогащена менее летучим (высококипящим) компонентом.Количественно оценку дистилляции проводят при помощи коэффициента разделения a:

В простейших системах a не зависит от состава системы и равен

Твердые растворы

Твердыми растворами называют однородные системы, состоящие из двух и более твердых компонентов.Способность образовывать твердые растворы свойственны всем кристаллическим твердым телам.В большинстве случаях твердые растворы образуются в узком интервале концентрации, значительно реже в широком интервале концентрации. Примеры: золото для ювелирных изделий (Au-Cu), драгоценные природные камни, слюда, полевые шпаты, сплавы металлов, сталь, чугун, латунь и др. В зависимости от способа получения и особенности взаимодействия компонентов твердые растворы делятся на растворы:1)замещения; 2) внедрения и 3) вычитания. Твердые растворы замещения образуются в результате замещения молекул, атомов и ионов в кристаллических решетках растворителя на молекулы, атомы и ионы растворенного вещества. Твердые растворы замещения образуют элементы, атомные радиусы которых отличаются не более чем на 15 %. К ним можно отнести сплав Cu-Ni.Твердые растворы внедрения образуют атомы радиусы которых существенно отличаются друг от друга.Такие растворы образуются когда неметаллы (бор, водород, кислород, азот, углерод) в металлах. К ним относятся чугун, сталь и др.В твердых растворах вычитания происходит «выпадение» атомов из кристаллической решетки. Такие системы иногда называют твердыми растворами с дефектами решетки. В зависимости от взаимной растворимости компонен-тов твердые растворы делятся на неограниченные и ограниченные твердые растворы. В зависимости от растворимости компонентов раство-ра различают системы,

1) компоненты которых взаимно неограниченно раствори-мы в жидком и твердом состоянии,

2) компоненты которых растворимы лишь в жидком состоянии, а в твердом состоянии не образуют раство-ры (растворы с эвтектикой).

Видео:SATI ETHNICA ｜ «Квартирник НТВ у Маргулиса»Скачать

Дипломная работа: Моделирование парожидкостного равновесия реакционной смеси в процессе получения метилциклопропилкетона

Федеральное агентство по образованию

МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ТОНКОЙ

ХИМИЧЕСКОЙ ТЕХНОЛОГИИ им. М.В.ЛОМОНОСОВА.

Кафедра химии и технологии основного органического синтеза.

Аттестационная работа по теме:

«Моделирование парожидкостного равновесия реакционной смеси в процессе получения метилциклопропилкетона»

на соискание степени бакалавра по направлению 550800

«Химическая технология и биотехнология».

Зам. зав. кафедрой, д.т.н., проф. Тимошенко А.В.

Научный руководитель, к.т.н., доцент Назанский С.Л.

Соискатель Кузнецова Г.П.

Москва, 2006 год.

Метилциклопропилкетон (МЦПК) – важный полупродукт органического синтеза. Одним из способов его получения является реакция разложения ацетопропилацетата с выделением уксусной кислоты (УК) [1]:

Также известен способ проведения этой реакции в присутствии щелочного катализатора при 400 – 425 0 С [1]. Селективность процесса по МЦПК достаточно высока (80%) при конверсии АПА 95 – 100%. Недостатками процесса являются высокая температура синтеза и практически полная потеря УК.

Наиболее простой способ связан действием на ацетопропилацетат (АПА) хлористого водорода, а затем щелочи без промежуточного выделения образующегося ацетопропилхлорида:

Получаемый этим способом МЦПК соответствует требованиям по чистоте, однако на 1 т целевого продукта образуется до 20 т отходов и полностью теряется уксусная кислота.

Третий вариант синтеза МЦПК связан с использованием катализаторов на основе окиси алюминия. Последние активны при температурах 250 – 260 0 С и позволяют количественно регенерировать УК, но не обладают достаточной селективностью. Экономические оценки показывают, что при условии достижения селективности 80 – 85% по МЦПК процесс с использованием катализатора на основе Al₂ O₃ может успешно конкурировать с вышеперечисленными методами.

В данной работе мы должны смоделировать парожидкостное равновесие и предложить наиболее удобный способ получения МЦПК для достижения максимально возможной конверсии в системе.

При анализе стационарных состояний проточных реакционных систем приходится сталкиваться с некоторым противоречием, суть которого особенно очевидна на примере реактора идеального смешения, в котором состав в реакторе совпадает с составом на выходе из него. В этом случае работа реактора при высоких скоростях химической реакции (при высоких концентрациях реагентов) приводит к низкой конверсии в аппарате и, наоборот, при низких скоростях химического превращения (высокие концентрации продуктов реакции) достигается высокая конверсия, которая в большинстве случаев ведет к снижению селективности [5]. Это свойственно реакторам любого типа. Таким образом, для проведения процесса при одновременно высоких значениях скорости химической реакции и конверсии необходимо, чтобы состав на выходе из реакционной зоны, который определяет скорость химической реакции, не совпадал с составом на выходе из системы, который определяет конверсию в ней. Это возможно лишь при организации селективного вывода продуктов реакции из системы с использованием массообменных процессов. Именно такой вывод компонентов реакционной смеси, независимо от способа его реализации (рециркуляционные или совмещенные реакционно-массообменные процессы), позволяет, с одной стороны, создавать в реакционной зоне необходимые условия для протекания целевых реакций с высокими скоростями (высокая производительность реактора по реагентам), а, с другой стороны, обеспечивать в системе в целом высокую конверсию (вплоть до полного исчерпывания реагентов) и селективность. Все это, в конечном счете, и является основой для создания современных энергосберегающих и экологически чистых технологий.

Можно выделить два основных способа реализации селективного вывода продуктов реакции из системы.

Первый, традиционный способ предполагает, что процессы синтеза и разделения проводятся последовательно и в разных аппаратах, например, в реакторе и ректификационной колонне, охваченных рециклом по реагентам. Это так называемые рециркуляционные процессы.

При реализации второго способа вывод продуктов реакции происходит непосредственно из реакционной зоны, т.е. процессы синтеза и разделения проводятся одновременно и в рамках одного массообменного аппарата, причем реакционная

зона как источник продуктов реакции размещается в области максимальной концентрации реагентов. Примерами таких процессов являются реактора, снабженные мембранами, ректификационные колонны, внутри которых размещена реакционная зона и т.д. Это так называемые совмещенные реакционно-массообменные процессы [6].

Очевидно, что в обоих способах тип используемого массообменного процесса или оборудования, реализующего селективный вывод продуктов реакции, определяется физико-химическими свойствами реакционной смеси. Если в основу классификации положить характер используемого разделительного процесса, то можно выделить следующие основные группы рециркуляционных и совмещенных процессов: реакционно-абсорбционные; реакционно-адсорбционные; реакционно-десорбционные; реакционно-кристаллизационные; реакционно-мембранные; реакционно-ректификационные, реакционно-экстракционные и т.д.

Теоретически полный селективный отвод продуктов реакции непосредственно из реакционной зоны может быть реализован с помощью идеальной мембраны, обладающей 100%-ой селективностью по отношению ко всем компонентам реакционной смеси и бесконечно большой производительностью. Это позволяет достигать максимальной скорости химической реакции (при закрепленных значениях констант скоростей), соответствующей присутствию в аппарате только реагентов. Кроме того, предположение об идеальной мембране позволяет осуществлять вывод продуктов со 100%-ой селективностью независимо от физико-химических свойств реакционной смеси. Очевидно, что в такой системе теоретически всегда может быть достигнуто полное исчерпывание реагентов.

Применение мембран особенно удобно при разделении азеотропных смесей, например, путем испарения жидкости на поверхности мембраны. Трудность реализации этого процесса заключается в необходимости подвода большого количества тепла к поверхности мембраны для испарения жидкости. Альтернативой этому методу является разделение предварительно испаренной жидкости.

Однако, к сожалению, существующие в настоящее время мембраны обладают рядом существенных недостатков: отсутствие 100%-ой селективности по отношению ко всем продуктам реакции; низкая производительность; недостаточная стойкость к высоким температурам и средам; возможность осаждения на рабочей поверхности трудно растворимых солей и продуктов смолообразования; непродолжительный срок службы мембраны и т.д.

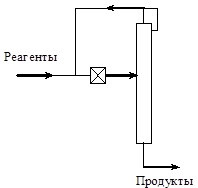
Все это делает весьма затруднительным их использование в непрерывных крупнотоннажных производствах. Поэтому на практике организация селективного вывода продуктов реакции из системы в основном осуществляется с использованием высокопроизводительных массообменных

процессов, таких как ректификация, экстракция, абсорбция и т.д.

Очевидно, что независимо от способа организации селективного обмена реакционной системы веществом с окружающей средой, условием стационарного режима ее работы является следующее балансовое соотношение

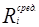
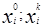
где — усредненная по объему скорость химической реакции по i-му реагенту; V-объем реакционной зоны; -мольные доли i — го компонента во входном и выходном потоках соответственно; F 0 ; F k — входной и выходной мольные потоки.

Правая часть этого выражения представляет собой производительность реакционной зоны по i-му реагенту. Если условия проведения химической реакции зафиксированы, т.е. заданы численные значения констант скоростей прямой и обратной реакций, то 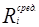является ограниченной функцией только от концентраций в реакционной зоне. В случае использования закона действующих масс максимальное значение этой функции будет достигаться, когда в реакционной зоне присутствуют только реагенты в стехиометрическом соотношении. Подставляя в уравнение максимальное значение усредненной скорости, получим минимальное значение объема реакционной зоны V_min , при котором заданная производительность, определяемая левой частью, теоретически еще может быть достигнута

Таким образом, это выражение определяет нижнюю оценку объема реакционной зоны V_min необходимого для достижения заданной производительности. Следовательно, можно утверждать, что необходимым условием достижения заданной производительности, является выражение

где V- рабочий объем реакционной зоны.

Очевидно, что в отличии от необходимых условий, достаточные условия реализации в системе заданной конверсии не могут быть сформулированы без привлечения дополнительной информации о том, какой из способов формирования требуемого состава в реакционной зоне используется и какими ограничениями обладает массообменный процесс, осуществляющий селективный вывод продуктов реакции из реакционной зоны или системы в целом. Следует отметить, что в любом случае для достижения полной конверсии по реагентам (отсутствие реагентов на выходе из системы) необходимо использовать идеализированный массообменный процесс, позволяющий осуществлять полное отделение продуктов реакции от реагентов, которые должны быть тем или иным способов возвращены в реакционную зону.

Для описания математической модели парожидкостного равновесия (ПЖР) в реальных системах пользуются обобщенным уравнением Рауля: ,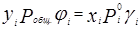

где γ_i – коэффициент активности i-го компонента в жидкой фазе, а φ_i – коэффициент летучести i-го компонента в паровой фазе. φ_i = 1, если ассоциация в паре и Р E определяют из коэффициентов активности. Ниже приведены основные уравнения:

Корреляция избыточных энергий Гиббса имеют чисто эмпирический характер или же частичное теоретическое обоснование. Обычно состав выражают в мольных долях х_i , однако, если молекулы значительно различаются по размерам и химической природе, лучше пользоваться объемными долями [3].

Эти уравнения указывают на тесную связь коэффициентов активности с избыточной энергией Гиббса G E [7]. Были предложены многочисленные модели, включающие в себя настраиваемые параметры, которые зависят от температуры. В некоторых случаях этой зависимостью можно пренебречь, особенно если температурный интервал невелик. На практике число настраиваемых констант в расчете на бинарное взаимодействие обычно равно двум или трем; чем больше число констант, тем лучше будет представление экспериментальных данных, однако в то же время потребуется большое количество надежных экспериментальных данных для определения констант. Чтобы получить константы для бинарной смеси при определенной температуре числом более трех, необходимо иметь подробные и исключительно точные экспериментальные данные.

Для умеренно неидеальных бинарных смесей хорошие результаты дают все уравнения, содержащие два (или более) параметра бинарного взаимодействия; в таких случаях нет смысла разбирать преимущества той или иной модели. Следует только отметить, что старые модели (Маргулеса, Ван-Лаара) математически проще, чем более современные (Вильсона, NRTL, UNIQUAC).

Уравнение Маргулеса является наиболее старым из числа применяемых в настоящее время. Исследования Маргулеса были выполнены еще до того, как были сформулированы такие понятия, как фугитивность и коэффициенты активности, однако в сущности его предложения сводятся к представлению lnγ₁ и lnγ₂ в виде степенных рядов по составу:

для двухкомпонентных смесей.

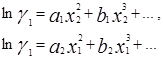
Как правило, применяют линейные перегруппировки этих рядов, предложенные Карлсоном и Кольборном [3]:

в которых существует постоянная зависимость между параметрами и коэффициентами активности при бесконечном разбавлении:

Избыточная энергия Гиббса, соответствующая этим уравнениям, составляет

Двухчленное (однопараметрическое) уравнение Маргулеса применимо только для простых смесей, в которых компоненты похожи по химической природе и размеру молекул [4].

Ван-Лаар рассмотрел изобарный процесс образования жидкого раствора из компонентов, включающий стадии испарения чистых веществ, их смешения в разреженном идеальном газовом состоянии и последующего сжатия и конденсации смеси до исходного давления. Он допускал нулевые значения избыточных объемов и энтропии процесса (соответственно, избыточная энергия Гиббса равна избыточной внутренней энергии) и подчинение флюидных фаз уравнению состояния Ван-дер-Ваальса, причем константы этого уравнения для смесей он представил с помощью простых комбинационных правил на основе констант для чистых компонентов [7]. Ван-Лаар просуммировал изменение внутренней энергии на отдельных стадиях процесса образования раствора, результат может быть представлен в виде следующих уравнений для G E и γ_i в бинарной системе:

В модели Ван-Лаара величины А, В аналитически связаны с константами уравнения Ван-дер-Ваальса, однако выяснилось, что последние не обеспечивают адекватное описание систем, в частности, из-за большой чувствительности модели к произвольно выбранным комбинационным правилам для констант уравнения состояния. Если же рассматривать величины А, В как самостоятельные эмпирические параметры, оцениваемы по экспериментальным данным о бинарной системе, тогда соотношения превращаются в простые корреляционные уравнения, удовлетворительно описывающие многие системы[7].

Точность представленных выше моделей обычно удовлетворительна для систем малой или умеренной неидеальности и недостаточна для систем с большими отклонениями от идеального поведения.

Прогресс в методах расчета фазовых равновесий, наблюдающийся с середины 60-х гг., в значительной мере связан с появлением нового типа уравнений для G E и γ_i , за которыми закрепилось общее название – уравнения (модели) локального состава. При их выводе существенную роль, как это следует из названия, играет представление о локальном, микроскопическом составе раствора [7].

В моделях локального состава относительное различие локальных и средних концентраций компонентов связывают с разностью энергий взаимодействия одноименных и разноименных молекулярных пар распределением типа больцмановского.

Введение локальных концентраций в приближенные теоретические уравнения открывает дополнительные возможности для учета энергетики межмолекулярных взаимодействий.

Энергетические параметры моделей С_ij носят полуэмпирический характер и оцениваются по экспериментальным термодинамическим данным.

То обстоятельство, что уравнения локального состава описываются на молекулярные модели растворов, обеспечивает им ряд преимуществ перед более ранними уравнениями для коэффициентов активности. Наиболее отчетливо эти преимущества проявляются в случае предсказания свойств многокомпонентных систем по данным для бинарных, при расчетах для неизотермических условий и при описании сильно неидеальных систем. Первое из уравнений такого рода было предложено в 1964 г. Вильсоном [7].

При разработке уравнения Вильсон исходил из тог, что межмолекулярные взаимодействия зависят в первую очередь от «локальных концентраций» ,которые он выражал в объемных долях [3].

Уравнение Вильсона для бинарной смеси для избыточной свободной энергии смешения и для определения коэффициентов активности имеет следующий вид:

где

— мольный объём j – го компонента; — мольная доля j – го компонента; член — величина, пропорциональная энергии взаимодействия разноименных молекул; член является константой, пропорциональной энергии взаимодействия между одноименными молекулами.

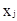
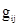
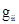
Уравнения для бинарной системы содержат два параметра, которые оценивают по экспериментальным данным для этой системы. Уравнения для многокомпонентного раствора содержат только параметры составляющих бинарных систем. Таким образом, равновесие в многокомпонентных системах предсказывается по данным о бинарных. В этом состоит главное преимущество уравнений Вильсона (и других уравнений локального состава) перед более ранними уравнениями для коэффициентов активности.

Другое достоинство модели Вильсона в приближенном учете влияния температуры на G E и γ_i . При С_ij =const температурная зависимость передается через величины λ_ij . Это облегчает описание парожидкостного равновесия в неизотермических условиях.

Серьезный недостаток модели Вильсона – ее неспособность описывать свойства расслаивающихся растворов (ни при каких значениях параметров модели не удовлетворяется термодинамическое условие неустойчивости системы относительно образования новой фазы).

Одна из модификаций уравнения Вильсона была предложена Цубокой и Катаямой. Для расчетов избыточной энергии Гиббса эти авторы используют следующее выражение:

где V_ij (=V_i /V_j ) – соотношения молярных объемов, и если эти соотношения равны единице, то получаем уравнение Вильсона. Уравнения для определения коэффициентов активности бинарных смесей соответственно принимают следующий вид [3]:

В системах с гомогенными растворами уравнение Цубоки – Катаямы дают в среднем те же результаты, что и уравнения Вильсона, однако, в отличие от последних, они применимы и к расслаивающимся растворам. По качеству описания равновесий жидких фаз они нередко превосходят уравнения NRTL, несмотря на меньшее число оцениваемых параметров.

Уравнение NRTL для избыточной энергии Гиббса выводят, основываясь на теории, согласно которой жидкость в двухкомпонентной смеси имеет ячеистую структуру. Причем эти ячейки состоят из молекул типа 1 и 2, каждая из которых окружена такими же молекулами, которые в свою очередь имеют аналогичное окружение, и т.д. Гиббсовы энергии взаимодействия между молекулами обозначают символом g_ij , где подстрочным индексом j указывают центральную молекулу; таким же образом обозначают и мольные доли в окружающих зонах х_ij .

G_ij =exp(-α_ij τ_ij ) ; τ_ij =C_ij /RT ;

Общее число независимых параметров уравнения, описывающего бинарный раствор, равно трем: α_ij , C_ij , C_ji . При недостаточно полной или недостаточно точной экспериментальной информации о системе оценка параметра α_ij ненадежна. В этом случае его значение часто задают априори – в соответствии с химической природой системы и следующими рекомендациями авторов уравнения:

α_ij = 0,2 для смесей насыщенных углеводородов с полярными неассоциированными жидкостями, для систем с малой взаимной растворимостью компонентов;

α_ij = 0,3 для систем с небольшими отклонениями от идеальности, для смесей воды с полярными растворителями;

α_ij = 0,4 для смесей насыщенных углеводородов с перфторуглеводородами;

α_ij = 0,47 для смесей полярных веществ (например, спиртов, пиридина) с неполярными веществами, с водой, для смесей полярных веществ с четыреххлористым углеродом.

Математическая форма уравнений обеспечивает модели NRTL большую гибкость, способность описывать самые различные типы зависимости коэффициентов активности от состава. Сохраняя основные достоинства уравнений Вильсона, уравнения NRTL способны также описывать системы с расслаиванием, благодаря чему часто используются для расчета равновесий жидкость – жидкость и жидкость – жидкость – пар [7].

Преимущества и недостатки уравнения NRTL [3].

При помощи трехпараметрического уравнения NRTL можно, как правило, достаточно хорошо представит данные о равновесии в бинарных системах. Преимущество этого уравнения по сравнению с уравнениями Маргулеса и Ван-Лаара состоит в том. Что его можно применять к многокомпонентным смесям, основываясь только на бинарных параметрах, а по сравнению с уравнениями Вильсона – в том, что его можно использовать для представления равновесия жидкость-жидкость, хотя уравнение Цубоки-Катаямы-Вильсона также применимо в этих целях. В некоторых случаях какое-либо одно из уравнений дает лучшие результаты при описании равновесия пар-жидкость, но поскольку уравнение NRTL трехпараметрическое, оно обычно предпочтительнее, чем уравнение Вильсона или UNIQUAC.

При выводе уравнения UNIQUAC ,носившим получеткий характер, Абрамс и Праузниц исходили из модели двух жидкостей и концепции локального состава. Используемая ими модель предполагает, что избыточная энергия Гиббса обусловлена, во-первых, различием размеров и форм молекул (конфигурационная или комбинаторная составляющие) и, во-вторых, энергией взаимодействия молекул (вторая составляющая избыточной энергии Гиббса) [3].

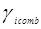
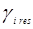
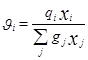
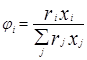
g_i – параметр площади компонента i; r_i – параметр объема компонента i;z – координационное число;— комбинаторная часть коэффициента активности компонента i; — остаточная часть активности компонента i;— доля площади компонента i; — объемная доля компонента i.

По качеству описания равновесий жидкость – пар и жидкость – жидкость модель UNIQUAC в среднем соответствует модели NRTL, но содержит, в расчете на пару компонентов, на один оцениваемый параметр меньше. Последнее важно при расчете параметров для бинарных систем с малой взаимной растворимостью компонентов, когда для обоснованного расчета трех параметров данных недостаточно, а также в любом другом случае очень ограниченной экспериментальной информации о системе. Ценное свойство модели – учет в явной форме комбинаторного вклада в G Е , что позволяет применить модель к растворам полимеров [7].

Уравнение Маргулиса, Ван Лара и связанные с ними алгебраические выражения характеризуются относительной простотой математического аппарата, легкостью оценки параметров по данным о коэффициентах активности и адекватным представлением двухкомпонентных смесей, значительно отклоняющихся от идеальных, включая частично растворимые жидкие системы. Эти уравнения не применимы к многокомпонентным системам, если отсутствуют параметры взаимодействия между тремя и более компонентами.

Уравнение Вильсона позволяет точно представить равновесие пар – жидкость в двух- и многокомпонентных смесях с использованием только параметров бинарного взаимодействия. В силу большей простоты этого уравнения его использование может быть предпочтительным для решения указанной задачи, чем применение уравнений NRTLи UNIQUAC. Уравнение Вильсона нельзя непосредственно применять для представления равновесия жидкость – жидкость; использование в этих целях его столь же простой модификации, уравнения Цубуки – Катаямы – Вильсона, дает удовлетворительные результаты, хотя последнее не было подвергнуто тщательной экспериментальной проверке, как другие уравнения.

При помощи уравнения NRTL можно достаточно верно представить равновесие пар – жидкость и жидкость – жидкость в двух- и многокомпонентных системах, а применительно к водным системам оно часто превосходит другие уравнения. Это уравнение проще по форме, чем уравнение UNIQUAC, однако его недостаток состоит в том, что для каждой пары составляющих необходимы три параметра. Величину третьего параметра часто можно получить исходя из химической природы компонентов.

Уравнение UNIQUAC – наиболее сложное в алгебраическом отношении, хотя в нем используется только по два параметра для каждой пары компонентов. В уравнении учитываются сведения о площадях поверхности и объемах молекул чистых компонентов, которые можно определить по данным о структуре, в силу чего этот метод представляется особенно эффективным применительно к смесям, молекулы которых значительно различаются по размеру. Уравнение UNIQUAC применимо для представления равновесия пар – жидкость и жидкость – жидкость в многокомпонентных смесях при использовании только параметров бинарного взаимодействия и данных о чистых компонентах [3].

Математическое описание совмещенных реакционно-ректификационных процессов, а также синтез принципиальной технологической схемы получения конечных продуктов предполагает обязательное наличие данных по фазовому равновесию жидкость – пар, в связи, с чем исследование и математическое описание условий парожидкостного равновесия является одной из важнейших задач. Экспериментальное определение равновесия жидкость – пар в многокомпонентных системах весьма трудоемко. Поэтому целесообразно провести исследования в составляющих наименьшей размерности (бинарных, тройных системах) и в случае адекватного описания этих данных фазовые равновесия в системах большей размерности моделируются с незначительной ошибкой, сопоставимой с ошибкой эксперимента.

Моделирование фазового равновесия в реакционной смеси, содержащей АПА, МЦПК и УК, проводилось на основе уравнений «локальных составов», учитывающих связь между избыточной энергией Гиббса и параметрами; характеризующими различие в размерах молекул и в величинах межмолекулярного взаимодействия неидеальных растворов.

Уравнения Вильсона, NRTL и UNIQUAC были использованы для моделирования парожидкостного равновесия в бинарной системе МЦПК-УК, а также АПА-МЦПК, АПА-УК и трехкомпонентной системе АПА-МЦПК-УК. Данная смесь содержит бинарный гомогенный азеотроп с минимумом температуры кипения на стороне МЦПК-УК. Результаты приведены в таблице:

На основе полученных данных можно сделать вывод, что для описания парожидкостного равновесия реакционной смеси получения МЦПК наилучшей моделью является NRTL.

Видео:Юля Паршута - Квартирник у Маргулиса (LIVE, 2023)Скачать

Парциальные молярные величины. Физический смыл ПМВ. Уравнение Гиббса-Дюгема и Дюгема-Маргулиса. Методы определения ПМВ.

Общая характеристика растворов. Способы выражения состава растворов.

Раствор – гомогенная система, состоящая из двух или более компонентов, состав которой может меняться в пределах определяемой взаимной растворимостью веществ. Растворы занимают промежуточное положение между химическими соединениями и мех смесями веществ. Общее: 1)с химическими соединениями: однородность системы 2) со смесями: примесный состав. Отличие 1) от хим соединений: переменный состав и сила связей между частицами 2) от смесей: гомогенность системы. Раствор – термодинамически устойчивая система, т.к. процесс его образования является самопроизвольным, т.е. сопровождается уменьшением свободной энергии системы. Взаимное растворение компонентов продолжается до тех про, пока не наступает состояние равновесия (состояние насыщения). Наиболее важная характеристика раствора – состав, который количественно выражается разными способами: 1) Мольная доля (или мольный %). N_i = [n_­i­/(n­₁ + n₂ + …)]*100%. 2) Объемная доля (или объемный %). φ_i = [V_i/(V₁ + V₂…)]*100%. Для газов мольный % и объемный % равны. 3) Массовый процент ω (аналогично). 4) Молярная концентрация (молярность) С_i = n_i/V = ω*ρ/M_i. (моль/дм 3 ). 5)Моляльная концентрация (моляльность) m_i = n_i / g₁ = g_i­*1000/M_i*g₁. 6) Мольное отношение. R_2/1 = n₂/n₁.

Формальная кинетика обратимых реакций второго порядка.

А+В = С+Д (k₁ u k₂ – константы скорости прямой и обратной реакций). Рассмотрим наиболее простой случай, когда количество моль в начальный момент времени t=0 одинаковы и равны величине а. Количество моль конечных веществ равны 0. V=const. Основное кинетическое уравнение скорости реакции имеет вид: dx/dt = k₁*(a – x) 2 – k₂x 2 . Или dx/dt = (k₁ – k₂)*(x 2 – 2k₁ax/(k₁ – k₂) + k₁a 2 /(k₁ – k₂)). Выражение в скобках – это квадратное уравнение. Обозначим его корни m₁ u m₂. Его можно записать так: dx/dt = (k₁ – k₂)*(m₁ – x)*(m₂— x). После преобразований получим выражение для расчета разности константа скоростей: k₁ – k₂ = 1/t * 1/(m₁ – m₂) * ln[ (m₂*(m­₁ – x))/m₁(m₂ – x))]. Зная К = k(прямой) / k (обратной) можно найти k₁ u k₂.

1. ЭДС гальванического элемента, работающего за счет реакции Cd + РЬС1₂ = CdCl₂ + Pb равна 0,1880 В при 298 К, (dE/dT)_P = -4,8-10 -4 В/К. Вычислите тепловой эффект реакции и изменение энтропии.

Дано: n=2; E=0,188В; T=298K; (dE/dT)_P = -4,8-10 -4 В/К; Найти: ΔH?,ΔS? Решение: ΔH=ΔS+TΔS; ΔG=-nFE= -2∙96500∙0,188=-36284 Дж/моль. ΔS=nF∙(dE/dT)_P =2∙96500∙(-4,8-10 -4 )=-92,6 Дж/моль∙К. ΔH=-36284+298∙(-92,6)=-63890,7 Дж/моль.

2. Зависимость константы скорости некоторой реакции от температуры выражается уравнением: In к = -27456/T +5lnT+45,76. Вычислите энергию активации при температуре 300 К.

Дано: Ур-е, Т=300К. Найти: Е? Решение: Е=RT²(dlnk/dT); dlnk/dT=27456/T² + 5/T; E= RT²(27456/T² + 5/T); E=R∙27456+5RT=8,314∙27456+5∙8,314∙300=240740.

БИЛЕТ 2.

Парциальные молярные величины. Физический смыл ПМВ. Уравнение Гиббса-Дюгема и Дюгема-Маргулиса. Методы определения ПМВ.

Вещество, становясь компонентом раствора теряет свою индивидуальность. Для характеристики доли, которую вносит каждый компонент в то или иное термодинамическое свойство раствора используется ПМВ. Все свойства растворов делятся на: а) Экстенсивные (зависят от количества вещества). V, S, H…. Такие свойства в системе суммируются, т.е. обладают свойством аддитивности. б) Интенсивные. (не зависят от количества вещества). Т, Р, хим потенциал… Такие свойства в системе выравниваются. ПМВ компонента раствора называют частную производную от какой-либо экстенсивной величины g по числу моль одного из компонентов n_i при условии постоянства Р, Т и чисел моль всех остальных компонентов раствора n_j(j+i). g_i (с чертой) = (бg/бn_i) _P,T,nj .Физический смысл ПМВ. Она равна величине изменения экстенсивного свойства раствора, если при постоянстве Р,Т добавляется 1 моль i-го компонента к весьма большому объему данной концентрации. ПМВ может принимать как положительные, так и отрицательные значения: положительные – при добавлении данного компонента происходит увеличение свойства раствора. Отрицательные – при добавлении… уменьшение свойства раствора. Наиболее важными ПМВ являются: (все с чертой наверху. ) 1) V_i = (бV/бn_i)_P,T,nj парциальный молярный объем. 2) ΔS_i = (бΔS/ бn_i)_P,T,nj – парциальное молярное изменение энтропии. 3) ΔН_i =…. Парциальное молярное изменение энтальпии. 4) хим потенциал μ = G_i = (бG/ бn_i)_P,T,nj парциальная молярная энергия Гиббса. Методы определения ПМВ. Наиболее часто используют 2 метода: 1) Аналитический. Необходимо иметь зависимость данного экстенсивного свойства от состава раствора в виде уравнения. Для определения ПМВ это уравнение дифференцируют по числу моль данного компонента и в полученное уравнение подставляют данное значение состава раствора. 2) Графический. По экспериментальным данным строят зависимость экстенсивного свойства раствора от его состава. При заданном составе n₂ проводим касательную. ПМВ = tgα = Δy/ Δx. (Лаба № 10). Уравнения Гиббса – Дюгема. (связь между ПМВ компонентов). При постоянстве Р, Т изменение экстенсивного свойства раствора dg не зависит от способа, которым осуществлялось это изменение, т.е. математически можно сделать так: dg=(бg/ бn₁)_P,T,nj*dn₁ + (бg/ бn₂)_P,T,nj*dn₂ + … = g₁ (с чертой)*dn₁ + g₂ (с чертой)*dn₂ + … (*) Чтобы найти величину самого свойства g, нужно проинтегрировать это уравнение. Пусть данному раствору прибавляют малые порции раствора той же концентрации. При этом допущении g₁ (с чертой), g₂ (с чертой)… не будут изменяться, следовательно, после интегрирования получится: (1) g = g₁ (с чертой)*n₁ + g₂ (с чертой)*n₂ + …Если одновременно изменять и количество и состав раствора, то изменение экстенсивного свойства dg будет находиться как полный дифференциал от уравнения (1), т.е.: dg = g₁ (с чертой)*dn₁ + n₁*dg₁(с чертой) + g₂ (с чертой)*dn₂ + n₂*dg₂(с чертой) + … = dg = g₁ (с чертой)*dn₁ + g₂ (с чертой)*dn₂ + … + n₁*dg₁(с чертой) + n₂*dg₂(с чертой) + …(**) Сравним (*) и (**). Следовательно: (2) n₁*dg₁(с чертой) + n₂*dg₂(с чертой) + … = 0.Уравнения (1) и (2) – уравнения Гиббса — Дюгема. Рассмотрим частные случаи: Пусть раствор бинарный, тогда уравнение (2) примет вид: а) n₁*dg₁(с чертой) + n₂*dg₂(с чертой) = 0. Поделим на (n₁ + n₂). Получим (3) N₁*dg₁(с чертой) + N₂*dg₂(с чертой) = 0 – Уравнение Г-Д через мольные доли. б) если ПМВ g_i (c чертой) = μ_i (хим потенциал), то: (4) N₁*dμ₁ + N₂*dμ₂ = 0— Уравнение Г-Д через хим потенциал. в) Если μ_i = μ_i 0 + RTlnP_i, тогда dμ_i = RTdlnP_i. Подставим в (4)и сократим на RT. Получим: (5) N₁*dlnP₁ + N₂*d lnP₂ = 0— Уравнение Дюгема – Маргулиса.

2.Формальная кинетика обратимых реакций первого порядка.А=В (k₁ u k₂ – константы скорости прямой и обратной реакций). Основное кинетическое уравнение скорости реакции: (*) dx/dt = k₁*(a – x) – k­₂*(b + x), где а и b – соответственно исходные количества вещества А и В моль. х – количество вещества А, прореагировавшее к моменту времени t моль. После преобразований получим выражение: (1) dx/dt = (k₁ + k₂)*((k₁a – k₂b)/(k₁ + k₂) – x). Обозначим (k₁a – k₂b)/(k₁ + k₂) = L. dx/dt = (k₁ + k₂)*(L – x). После интегрирования получим уравнение для расчета суммы констант скоростей: k₁ + k₂ = 1/t * ln[L/(L – x)]. Следовательно, для нахождения суммы скоростей нужно знать L. Ее можно найти деля числитель и знаменатель в уравнении (1) на k₂. и зная, что k₁/k₂ = K – константа равновесия. (Ка – b)/(1 + K) = L. Для нахождения К рассуждаем следующим образом: в момент равновесия скорости прямой υ₁ и обратной υ₂ равны. Значит dx/dt = 0. Подставив в уравнение (*) и обозначив через х₀ количество вещества А прореагировавшего к моменту равновесия получим: k₁*(a – x₀) – k₂*(b+x₀) = 0. Тогда К = k₁ / k₂ = (b + x₀)/ (a – x₀). Зная К можно найти L по уравнению k₁ + k₂ = 1/t * ln[L/(L – x)] сумму (k₁ + k₂) и рассчитать значение каждой константы.

1. Вычислите активность La(NO₃)3 в 0,01 моляльном растворе, если γ_± = 0,571.

2. Раствор слабой кислоты Н₂А при разведении 32 л/моль имеет эквивалентную электропроводность 9,2 см 2 /(моль-экв-Ом), а при бесконечном разведении она равна 389 см 2 /(моль-экв-Ом). Определите константу диссоциации кислоты.

Дано: Н₂А-к-та; V=32 л/моль; λ=9,2 см 2 /(моль-экв-Ом); λ0=389 см 2 /(моль-экв-Ом). Найти: Кд? Решение: Н₂А (c(1-α) )=2H+ (2αc)+A2- (αc); Kд=[H+]²∙[A2-]/[H2A]; Kд=(2αc)²∙ (αc)/ c(1-α)=4α³с²/1-α; α=λ/λ0=9,2/389=0,024; c=1/V=1/32=0,03; Kд=4∙0,024³∙0,03²/1-0,024=5,1∙10^-8 (моль/л)²

БИЛЕТ 3.

Дата добавления: 2015-07-20 ; просмотров: 1228 | Нарушение авторских прав

🔥 Видео

Алексею Романову - 70! «Топор в озере» (Квартирник у Маргулиса)Скачать

Евгений Маргулис | Квартирник наоборот. Кто лучше всех играет блюз? #67Скачать

ПЕЛАГЕЯ в программе «Квартирник НТВ у Маргулиса»Скачать

'АнимациЯ' 'Квартирник НТВ у Маргулиса' 2021 годСкачать

ЙОРШ. Квартирник у Маргулиса на НТВ.Скачать

Академия современной музыки Алексея Белова и Ольги Кормухиной | Квартирник Маргулиса, 2023Скачать

25/17 на "Квартирнике у Маргулиса" (2023)Скачать

КУРАРА. Квартирник НТВ у Маргулиса (2022)Скачать

Backstage. Григорий Лепс на «Квартирнике у Маргулиса»Скачать

Квартирник у Маргулиса 5 | ЧижСкачать

Квартирник НТВ у Маргулиса. ЛицейСкачать

Квартирник НТВ у Маргулиса: БИРТМАНСкачать

Вадяра Блюз - Квартирник у МаргулисаСкачать