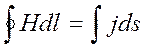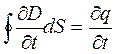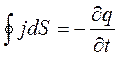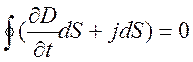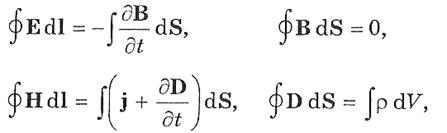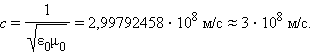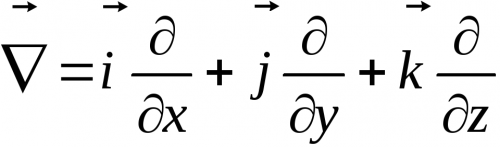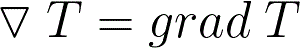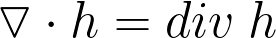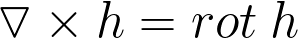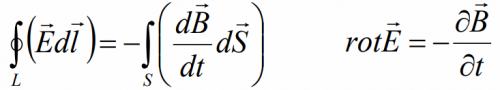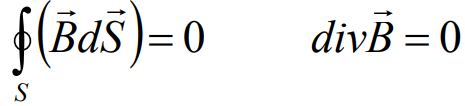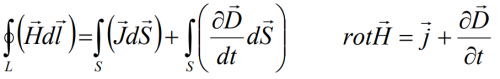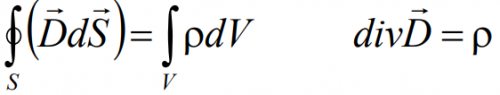2. Система уравнений Максвелла

3. ЭМ волны и их характеристики

4. Получение ЭМ волн – опыты Герца

5. Применение ЭМ волн

1. В реальной жизни не существует отдельно электрического и магнитного полей, есть единое электромагнитное поле.

Теория электромагнитного поля, на­чала которой заложил Фарадей, математически была заверше­на Максвеллом. Важной выдвинутой Максвеллом идеей, была мысль о симметрии во взаимо­зависимости электрического и магнитного полей. А именно, поскольку меняющееся во времени магнитное поле (dB/dt) со­здает электрическое поле, следует ожидать, что меняющееся во времени электрическое поле (dE/dt) создает магнитное поле.

Согласно теореме о циркуля­ции вектора Н

Применим эту теорему к случаю, когда предварительно заряженный плоский конденсатор разряжается через некоторое внешнее сопротивление (рис. а).

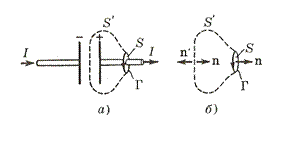
В качестве контура Г возьмем кривую, охватывающую провод. На контур Г можно натянуть разные поверхности, на­пример S и S’. Обе поверх­ности имеют «равные права», однако через поверхность S течет ток I, а через поверх­ность S’ нет тока. Поверхность S’ «прони­зывает» только электрическое поле. По теореме Гаусса поток вектора D сквозь замкнутую поверхность

D dS = q

Согласно определения плотности тока имеем

Сложим левые и правые части уравнений, получим

Из уравнения видно, что кроме плотности тока проводимости j имеется еще одно слагаемое dD/dt,размерность которого равна размерности плотности тока.

Максвелл назвал это слагаемое плотностью тока смещения:

Сумму же тока проводимости и тока смещения называют полным током.

Линии полного тока являются непрерывны­ми в отличие от линий тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения.

Следует иметь в виду, что ток смещения эквивалентен току проводимости толь­ко в отношении способности создавать магнитное поле.

Токи смещения существуют лишь там, где меняется со вре­менем электрическое поле. В сущности он сам является переменным электрическим полем.

Открытие Максвеллом тока смещения — чисто теоретическое открытие, причем первосте­пенной важности.

2. С введением тока смещения макроскопическая теория электромагнитного поля была завершена. Открытие тока смещения (dD/dt) позволило Максвеллу создать единую теорию электриче­ских и магнитных явлений. Теория Максвелла не только объяс­нила все разрозненные явления электричества и магнетизма, но и предсказала ряд новых яв­лений, существование которых подтвердилось впоследствии.

В основе электромагнитной теории Максвелла лежат четыре фунда­ментальных уравнений электродинамики, называемые уравне­ниями Максвелла.

Эти уравнения в сжатой форме выражают всю совокупность наших сведений об электромагнитном поле.

Содержание этих уравнений заключается в следующем:

1. Циркуляция вектора Е по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным конту­ром. При этом под Е понимается не только вихревое электриче­ское поле, но и электростатическое.

2. Поток вектора В сквозь произвольную замкнутую поверх­ность всегда равен нулю.

3. Циркуляция вектора Н по любому замкнутому контуру равна полному току (току проводимости и току смещения) че­рез произвольную поверхность, ограниченную данным конту­ром.

4. Поток вектора D сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.

Из уравнений Максвелла для циркуляции векторов Е и Н следует, что электрическое и магнитное поля нельзя рассмат­ривать как независимые: изменение во времени одного из этих полей приводит к появлению другого. Поэтому имеет смысл лишь совокупность этих полей, описывающая единое электро­магнитное поле.

Эти уравнения говорят о том, что электрическое поле может возникнуть по двум причинам. Во-первых, его источником яв­ляются электрические заряды, как сторонние, так и связан­ные. Во-вторых, поле Е образу­ется всегда, когда меняется во времени магнитное поле.

Эти же уравнения говорят о том, что магнитное поле В мо­жет возбуждаться либо движущимися электрическими заряда­ми (электрическими токами), либо переменными электриче­скими полями, либо тем и другим одновременно. Никаких ис­точников магнитного поля, подобных электрическим зарядам, в природе не существует, это следует из второго уравнения.

Значение уравнений Максвелла не только в том, что они выражают основные законы электро­магнитного поля, но и в том, что путем их решения (интегриро­вания) могут быть найдены сами поля Е и В.

Уравнения Максвелла обладают большей общностью, они справедливы и в тех случаях, когда существуют повер­хности разрыва — поверхности, на которых свойства среды или полей меняются скачкообразно.

Фундаментальные уравнения Максвелла еще не составляют полной системы уравнений элек­тромагнитного поля. Этих уравнений недостаточно для нахож­дения полей по заданным распределениям зарядов и токов. Их необходимо дополнить соотношениями, эти соотношения называют материаль­ными уравнениями.

Материальные уравнения наиболее просты в случае доста­точно слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных сред, материальные уравнения имеют следующий вид:

=εε₀

=μμ₀

=γ( + _ст)

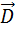
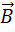
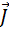
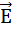
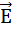
Уравнения Максвелла обладают рядом свойств.

1 свойства – линейности.

Уравнения Максвелла линейны, т.к. они содержат только пер­вые производные полей Е и В по времени и пространственным координатам и первые степени плотности электрических заря­дов и токов.

Свойство линейности уравнений Максвелла не­посредственно связано с принципом суперпозиции: если два ка­ких-нибудь поля удовлетворяют уравнениям Максвелла, то это относится и к сумме этих полей.

2 свойство – непрерывности.

Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда.

3 свойство – инвариантности.

Уравнения Максвелла выполняются во всех инерциальных системах отсчета. Они являются релятивистски инвариантны­ми. Это есть следствие принципа относительности, согласно ко­торому все инерциальные системы отсчета физически эквива­лентны друг другу. Факт инвариантности уравнений Максвел­ла подтверждается многочисленными опытными данными.

Уравнения Максвелла являются правильными реляти­вистскими уравнениями в отличие, например, от уравнений механики Ньютона.

4 свойство – симметрии.

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существу­ют электрические заряды, но нет зарядов магнитных.

В нейтральной од­нородной непроводящей среде уравнения Мак­свелла приобретают симметричный вид.

Из уравнений Максвелла сле­дует вывод о существовании принципиально нового физического явления: электромагнитное поле способно сущест­вовать самостоятельно — без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Поля такого рода называют электромагнитными волнами.В вакууме они всегда распространяются со скоро­стью, равной скорости с.

Выяснилось также, что ток смещения (dD/dt) играет в этом явлении первостепенную роль. Именно его присутствие наряду с величиной dB/dt и означает возможность появления электро­магнитных волн. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля элек­трического, в свою очередь, возбуждает магнитное поле.

За счет непрерывного взаимопревращения или взаимодействия они и должны сохраняться — электромагнитное возмущение будет распространяться в пространстве.

Теория Максвелла не только предсказала возможность существования электромагнитных волн, но и позволила устано­вить все их основные свойства.

3. Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году.

Гипотеза Максвелла была лишь теоретическим предположением, не имеющим экспериментального подтверждения, однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений, описывающих взаимные превращения электрического и магнитного полей, то есть систему уравнений электромагнитного поля (уравнений Максвелла). Из теории Максвелла вытекает ряд важных выводов, одним из них явился вывод о существовании электромагнитных волн.

Электромагнитные волны поперечны – векторы 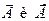перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис.).

Электромагнитные волны распространяются в веществе с конечной скоростью

,

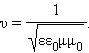
где ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные.

Скорость электромагнитных волн в вакууме (ε = μ = 1):

Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.

4. Максвелл утверждал, что электромагнитные волны обладают свойствами отражения, преломления, дифракции и т.д. Но любая теория становится доказанной лишь после ее подтверждения на практике. Но в то время ни сам Максвелл, ни кто-либо другой еще не умели экспериментально получать электромагнитные волны. Это произошло только после 1888 года, когда Герц экспериментально открыл электромагнитные волны.

В результате экспериментов Герц создал источник электромагнитных волн, названный им «вибратором». Вибратор состоял из двух проводящих сфер (в ряде опытов цилиндров) диаметром 10-30 см, укрепленных на концах проволочного разрезанного посредине стержня. Концы половин стержня в месте разреза оканчивались небольшими полированными шариками, образуя искровой промежуток в несколько миллиметров.

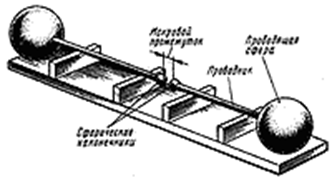
Сферы подсоединялись ко вторичной обмотке катушки Румкорфа, являвшейся источником высокого напряжения.

Из теории Максвелла известно,

1)излучать электромагнитную волну может только ускоренно движущийся заряд,

2)что энергия электромагнитной волны пропорциональна четвертой степени ее частоты.

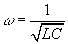
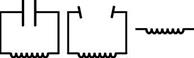
Понятно, что ускоренно заряды движутся в колебательном контуре, поэтому проще всего их использовать для излучения электромагнитных волн. Но надо сделать так чтобы частота колебаний зарядов стала как можно выше. Из формулы Томсона для циклической частоты колебаний в контуре следует, что для повышения частоты надо уменьшать емкость и индуктивность контура.

Чтобы уменьшить емкость C надо увеличивать расстояние между пластинами (раздвигать их, делать контур открытым) и уменьшать площадь пластин. Самая маленькая емкость, которая может получиться, — просто провод.

Чтобы уменьшить индуктивность L надо уменьшать число витков. В результате этих преобразований получим просто кусок провода или открытый колебательный контур ОКК.

Суть происходящих в вибраторе явлений заключается в следующем. Индуктор Румкорфа создает на концах своей вторичной обмотки очень высокое, порядка десятков киловольт, напряжение, заряжающее сферы зарядами противоположных знаков. В определенный момент в искровом промежутке вибратора возникает электрическая искра, делающая сопротивление его воздушного промежутка столь малым, что в вибраторе возникают высокочастотные затухающие колебания, длящиеся во все время существования искры. Поскольку вибратор представляет собой открытый колебательный контур, происходит излучение электромагнитных волн.

После огромной серии трудоемких и чрезвычайно остроумно поставленных опытов с использованием простейших, так сказать, подручных средств экспериментатор достиг цели. Удалось измерить длины волн и рассчитать скорость их распространения. Были доказаны

• интерференции и поляризации волн.
• измерена скорость электромагнитной волны

5. Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А. С. Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль для распространения и развития теории Максвелла.

Электромагнитные волны сантиметрового и миллиметрового диапазонов, встречая на своем пути преграды, отражаются от них. Это явление лежит в основе радиолокации — обнаружения предметов (например, самолетов, кораблей и т. д.) на больших расстояниях и точного определения их положения. Помимо этого, методы радиолокации используются для наблюдения прохождения и образования облаков, движения метеоритов в верхних слоях атмосферы и т. д.

Для электромагнитных волн характерно явление дифракции — огибание волнами различных препятствий. Именно благодаря дифракции радиоволн возможна устойчивая радиосвязь между удаленными пунктами, разделенными между собой выпук­лостью Земли. Длинные волны (сотни и тысячи метров) применяются в фототелеграфии, короткие волны (несколько метров и меньше) применяются в телевидении для передачи изображений на небольшие расстояния (немногим больше пределов прямой видимости). Электромагнитные волны используются также в радио-геодезии для очень точного определения расстояний с помощью радиосигналов, в радиоастрономии для исследования радиоизлучения небесных тел и т. д. Полное описание применения электромагнитных волн дать практически невозможно, так как нет областей науки и техники, где бы они не использовались.

Для осуществления радио- и телевизионной связи используются электромагнитные волны с частотой от нескольких сотен тысяч герц до сотен мегагерц.

При передаче по радио речи, музыки и других звуковых сигналов применяют различные виды модуляции высокочастотных (несущих) колебаний. Суть модуляции заключается в том, что высокочастотные колебания, вырабатываемые генератором, изменяют по закону низкой частоты. В этом и заключается один из принципов радиопередачи. Другим принципом является обратный процесс — детектирование. При радиоприеме из принятого антенной приемника модулированного сигнала нужно отфильтровать звуковые низкочастотные колебания.
С помощью радиоволн осуществляется передача на расстояние не только звуковых сигналов, но и изображения предметов.

Уравнение максвелла объяснение распространения электромагнитных возмущений в пространстве

Теория Д.К. Максвелла лежит в основе объяснения существования и свойств любых электромагнитных волн, таких, как световые волны, радиоволны, инфракрасное и ультрафиолетовое излучения. Эта теория является феноменологической, т.е. в ней не рассматриваются молекулярное строение среды и внутренний механизм процессов, происходящих в среде под действием электрического и магнитного полей. Электрические и магнитные свойства среды характеризуются относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью m и удельной электрической проводимостью σ. Предполагается, что эти параметры среды определяются из эксперимента.

Теория Максвелла — макроскопическая. Это означает, что рассматриваются макроскопические поля зарядов и токов, пространственные размеры которых неизмеримо больше размеров отдельных молекул и атомов.

Математическим выражением теории Максвелла служит система из четырех уравнений, которые записывают в двух формах — дифференциальной и интегральной.

Дифференциальные уравнения Максвелла получаются из интегральных с помощью двух теорем векторного анализа: теоремы Остроградского-Гаусса и теоремы Стокса.

Рассмотрим теорему Остроградского-Гаусса .

Пусть для характеристики какого-либо поля выбран вектор . Тогда поток вектора через произвольную замкнутую поверхность S, мысленно проведенную в этом поле, равен интегралу от дивергенции вектора , взятому по объему V, ограниченному замкнутой поверхностью S:

(4.1.1)

Операция дивергенции над произвольным вектором сводится к пространственной производной вида:

(4.1.2)

где a_x, a_y, a_z — проекции вектора на оси прямоугольной декартовой системы координат.

Рассмотрим теорему Стокса .

Пусть для характеристики какого-либо поля выбран вектор . Тогда циркуляция вектора вдоль произвольного замкнутого контура L, мысленно проведенного в этом поле, равна потоку вектора rot через поверхность S, ограниченную замкнутым контуром L:

(4.1.3)

Векторная операция rot в декартовых координатах выражается так:

(4.1.4)

Первое уравнение Максвелла

Это уравнение представляет собой обобщение закона электромагнитной индукции Фарадея:

(4.1.5)

Однако для произвольного контура выполняется взаимосвязь:

(4.1.6)

Поскольку в общем случае , то для не изменяющегося во времени контура имеет место соотношение:

(4.1.7)

Сравнивая (4.1.5) и (4.1.7) с учетом (4.1.6), для произвольного контура L, мысленно проведенного в переменном магнитном поле, можно записать:

(4.1.8)

Используя теорему Стокса, преобразуем (4.1.5):

(4.1.9)

Сравнивая подинтегральные выражения в (4.1.7) и в правой части (4.1.9), получим окончательно первое уравнение Максвелла в дифференциальной форме:

(4.1.10)

Физический смысл этого уравнения: переменное магнитное поле индуцирует вихревое электрическое поле.

Второе уравнение Максвелла

Используем теорему Гаусса для диэлектриков:

(4.1.11)

где — вектор электрической индукции, — вектор поляризации диэлектрика.

Продифференцируем (4.1.11) по времени:

(4.1.12)

Если поверхность S — неподвижна и не деформируется, то изменение во времени потока вектора электрической индукции может быть связано только с изменением по времени самого вектора электрической индукции:

(4.1.13)

Правая часть этой формулы имеет размерность тока, следовательно, величина имеет размерность плотности тока. Максвелл предложил назвать эту величину плотностью тока смещения :

(4.1.14)

Введя представление о токе смещения, Максвелл по-новому подошел к рассмотрению условия замкнутости цепей электрического тока. Как известно, цепи постоянного тока должны быть замкнутыми. Однако для цепей переменного тока это условие уже не является обязательным. Например, при зарядке и разрядке конденсатора постоянный электрический ток протекает по проводнику, соединяющему обкладки, но не проходит через диэлектрик, находящийся между обкладками. Следовательно, цепь не замкнута. Однако, с точки зрения Максвелла, для переменного тока такая цепь замыкается благодаря току смещения, который протекает через такой участок, где нет проводника, т.е. через диэлектрик. На таком участке благодаря наличию переменного тока смещения обязательно возникает переменное магнитное поле. Однако действие тока смещения, приводящее к возникновению магнитного поля, нельзя отделить от действия обычного тока проводимости. Например, для прямолинейного тока проводимости можно записать:

(4.1.15)

Линии магнитного поля направлены по касательным к концентрическим окружностям, окружающим проводник с током. Найдем циркуляцию магнитного поля по замкнутому контуру в виде окружности радиуса r:

(4.1.16)

Следовательно, магнитное поле прямолинейного проводника — вихревое (циркуляция вектора магнитного поля по замкнутому контуру не равна нулю).

Максвелл предположил, что в правой части соотношения (4.1.16) следует добавить ток смещения:

(4.1.17)

где ток смещения легко вычислить, используя (4.1.14):

(4.1.18)

Силу тока проводимости можно также представить в виде:

(4.1.19)

Согласно теореме Стокса для магнитного поля, имеем:

(4.1.20)

Подставляя (4.1.18) и (4.1.19) в (4.1.17) и сравнивая подинтегральные выражения в правой и левой частях, получаем второе уравнение Максвелла:

(4.1.21)

При отсутствии тока проводимости, тем не менее, может существовать переменное магнитное поле, обусловленное только током смещения:

(4.1.22)

Третье уравнение Максвелла

Максвелл обобщил теорему Гаусса для диэлектриков (4.1.11), предположив, что она справедлива для любого электрического поля, как стационарного, так и переменного. Запишем уравнение (4.1.11) в виде:

(4.1.23)

где ρ_своб — объемная плотность свободных зарядов, расположенных в объеме V, ограниченном замкнутой поверхностью S.

Тогда, используя теорему Остроградского-Гаусса для вектора электрической индукции, получим:

(4.1.24)

Сравнивая подинтегральные выражения в (4.1.23) и (4.1.24), получим третье уравнение Максвелла:

(4.1.25)

Четвертое уравнение Максвелла

Поскольку поток вектора магнитной индукции равен нулю:

(4.1.26)

то, используя теорему Остроградского-Гаусса для вектора магнитной индукции, легко получить четвертое уравнение Максвелла:

(4.1.27)

Такое равенство определяется отсутствием магнитных зарядов.

Итак, полная система уравнений Максвелла в дифференциальной форме включает в себя четыре дифференциальных уравнения:

(4.1.28)

Эту систему необходимо дополнить материальными уравнениями , которые характеризуют электрические, и магнитные свойства конкретных сред (веществ).

В случае изотропных несегнетоэлектрических и неферромагнитных сред и макроскопических токов, подчиняющихся закону Ома, эти уравнения в системе СИ имеют вид:

(4.1.29)

где ε₀ и μ₀ — электрическая и магнитная постоянные, ε и μ — относительная диэлектрическая и магнитная проницаемости среды, σ — удельная электропроводность вещества.

4.1.2. Свойства электромагнитных волн

Электромагнитной волной называется распространяющееся в пространстве с определенной скоростью электромагнитное поле. Как следует из уравнений Максвелла, переменное электрическое поле непременно порождает переменное магнитное поле, которое затем индуктирует переменное электрическое поле. Поэтому следует говорить о неразрывной связи переменных электрического и магнитного полей, называя это явление электромагнитным полем . Очевидно, что такой процесс должен происходить, циклически повторяясь, в течение неограниченного времени, если нет поглощения.

Существование электромагнитных волн непосредственно следует их уравнений Максвелла. Для области пространства, не содержащей свободных электрических зарядов и макроскопических токов, эти уравнения приобретают вид:

(4.1.30)

Используя материальные уравнения (4.1.29), эти уравнения можно представить в виде:

(4.1.31)

Если записать эти уравнения в проекциях на оси декартовой системы координат, то получим:

(4.1.33)

(4.1.34)

Используя первое из уравнений (4.1.33), можно получить:

(4.1.35)

Следовательно, компонента Е_х удовлетворяет волновому уравнению:

(4.1.36)

Если ввести обозначение для дифференциальной операции:

(4.1.37)

то волновое уравнение (4.1.37) можно представить в компактном виде:

(4.1.38)

Аналогичные уравнения могут быть получены и для всех других компонент электрического и магнитного полей. Суммируя результаты, окончательно можно представить волновые уравнения для электрического и магнитного полей в векторном виде:

(4.1.39)

Таким образом, переменное электромагнитное поле распространяется в среде в виде волн, фазовая скорость которых равна:

(4.1.40)

где

(4.1.41)

есть скорость электромагнитной волны в вакууме.

Оказалось, что с = 3·10 8 м/с, что совпадает со скоростью света в вакууме. Поэтому Максвелл задолго до экспериментального обнаружения электромагнитных волн (Г. Герц, 1888 г.) высказал гипотезу о том, что свет — это тоже электромагнитная волна.

Прямой проверкой можно показать, что решениями уравнений (4.1.39) служат плоские синусоидальные волны, которые удобно представить в форме Эйлера:

(4.1.42)

где ω — циклическая частота; — волновой вектор, перпендикулярный фронту плоской волны и задающий направление распространения волны; — радиус-вектор, задающий точки пространства.

Операция ротора может быть сведена к векторному произведению, например:

(4.1.43)

Тогда, используя решения (4.1.42), с помощью (4.1.43) имеем:

(4.1.44)

следовательно, применение этой операции сводится к векторному произведению.

Рассмотрим сейчас операцию:

(4.1.45)

Наконец, операцию дивергенции можно представить так:

(4.1.46)

Применяя результаты (4.1.44), (4.1.45) и (4.1.46) к уравнениям Максвелла (4.1.31), имеем:

или, окончательно:

(4.1.47)

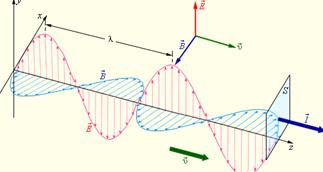
Из двух последних уравнений (4.1.47) следует, что , что указывает на поперечность электромагнитной волны. Из первого уравнения (4.1.47) ясно, что вектор Н как результат векторного произведения, должен быть перпендикулярен плоскости, в которой лежат вектора и . Аналогично, из второго уравнения (4.1.47) следует, что вектор электрического поля должен быть перпендикулярен плоскости, в которой лежат вектора и . Окончательно получается, что для любой электромагнитной волны вектора , и составляют тройку ортогональных векторов (Рис. 4.1.1).

4.1.3. Шкала электромагнитных волн

В зависимости от частоты ν = ω/2π или длины волны в вакууме λ₀ = с/ν, а также способа излучения и регистрации различают несколько видов электромагнитных волн:

• радиоволны;
• оптическое излучение;
• рентгеновское излучение;
• гамма-излучение.

Радиволнами называются электромагнитные волны, у которых длина волны в вакууме λ₀ > 5·10 -5 м (ν 12 Гц). Весь диапазон радиоволн принято делить на 9 поддиапазонов (Табл. 4.1.1).

Типы радиоволн

Название диапазона радиоволн	Длина волны, м	Частота, Гц
Сверхдлинные	Более 10 4	Менее 3·10 4
Длинные	10 4 ÷ 10 3	3·10 4 ÷ 3·10 5
Средние	10 3 ÷ 10 2	3·10 5 ÷ 3·10 6
Короткие	10 2 ÷ 10	3·10 6 ÷ 3·10 7
Метровые	10 ÷ 1	3·10 7 ÷ 3·10 8
Дециметровые	1 ÷ 0,1	3·10 8 ÷ 3·10 9
Сантиметровые	0,1 ÷ 0,01	3·10 9 ÷ 3·10 10
Миллиметровые	10 -2 ÷ 10 -3	3·10 10 ÷ 3·10 11
Субмиллиметровые	10 -3 ÷ 5·10 -5	3·10 11 ÷ 6·10 12

Оптическим излучением или светом называются электромагнитные волны, у которых длина волны в вакууме лежит в диапазоне 10 нм >λ₀ > 1 мм (границы условны). К оптическому излучению относят инфракрасное, видимое и ультрафиолетовое излучения.

Инфракрасным (ИК) называются электромагнитные волны, испускаемые нагретыми телами, у которых длина волны в вакууме лежит в диапазоне 1 мм > λ₀ > 770 нм.

Видимым излучением (светом) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 770 нм > λ₀ > 380 нм. Свет способен вызывать зрительные ощущения в человеческом глазе.

Ультрафиолетовым излучением (УФ) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 380 нм > λ₀ > 10 нм.

Рентгеновским излучением (рентгеновскими лучами) называются электромагнитные волны, которые возникают при взаимодействии заряженных частиц и фотонов с атомами вещества. Оно характеризуется длинами волны в вакууме в диапазоне с условными границами (10-100 нм) > λ₀ > (0,01-1 пм).

Гамма-излучением (γ-лучами) называются электромагнитные волны с длинами волны в вакууме 0,1 нм > λ₀. Это излучение испускается возбужденными атомными ядрами при радиоактивных превращениях и ядерных реакциях, а также возникает при распаде частиц, аннигиляции пар «частица-античастица» и других процессах.

4.1.4. Световая волна

Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других — как поток особых частиц (фотонов).

В электромагнитной волне колеблются векторы электрического и магнитного полей. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются наличием колебаний электрического вектора, который называют в этом случае световым вектором . Его изменения в пространстве и времени задаются уравнением плоской волны:

(4.1.48)

Здесь r — расстояние, отсчитываемое вдоль направления распространения волны.

Отношение скорости световой волны в вакууме с к ее фазовой скорости v в некоторой прозрачной среде называется абсолютным показателем преломления этой среды:

(4.1.49)

Показатель преломления связан с относительными диэлектрической и магнитной проницаемостями соотношением:

(4.1.50)

Для подавляющего большинства прозрачных веществ величина μ &#8776 1. Поэтому можно считать, что выполняется:

(4.1.51)

Значения показателя преломления характеризуют оптическую плотность среды. Среда с большим n будет более оптически плотной.

Длины волн видимого света в вакууме заключены в пределах:

(4.1.52)

В веществе длины волн будут другими. В случае колебаний с частотой ν длина волны света в вакууме равна:

(4.1.53)

Используя соотношение (4.1.49), имеем для длины света в веществе формулу:

(4.1.54)

Частоты видимого света лежат в пределах:

(4.1.55)

Модуль среднего по времени потока энергии, переносимого волной, называется интенсивностью света I в данной точке пространства. Интенсивность пропорциональна квадрату амплитуды волны:

I ∼ A 2

(4.1.56)

Световая волна, как и другие электромагнитные волны, является поперечной, т.е. направления колебаний электрического и магнитного векторов перпендикулярны к направлению ее распространения. В естественном свете присутствуют все направления колебаний электрического и магнитного векторов. Если в волне присутствуют колебания электрического вектора только в одной плоскости (а магнитного вектора в перпендикулярной плоскости), такую волну называют плоскополяризованной (линейно поляризованной) . Есть и более сложные случаи поляризации волн — круговая и эллиптическая. В случае круговой поляризации электрический и магнитный векторы вращаются по кругу с частотой изменения волны.

4.1.5. Геометрическая оптика

Длины воспринимаемых глазом световых волн очень малы (∼10 -7 м), поэтому распространение видимого света в первом приближении можно рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых прямых линий, называемых лучами. В предельном случае, когда длина волны света λ→0, законы оптики можно сформулировать на языке геометрии.

Основу геометрической оптики составляют 4 закона:

1. закон прямолинейного распространения света;
2. закон независимости световых лучей;
3. закон отражения света;
4. закон преломления света.

Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно . Этот закон является приближенным: при прохождении света через очень малые отверстия, размеры которых сравнимы с диной волны света, наблюдается отклонение от прямолинейности, тем большее, чем меньше отверстие.

Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга . Это означает, что пересечение лучей не мешает каждому из них распространяться независимо друг от друга. Этот закон справедлив при не слишком больших интенсивностях световых волн.

В основу геометрической оптики был положен принцип Ферма : свет распространяется по такому пути, для прохождения которого ему требуется минимальное время .

Пусть для прохождения участка ds свету требуется время dt = ds/v, где v — скорость света в данной точке среды. Поскольку v = c/n, то получим:

(4.1.57)

Следовательно, время τ, необходимое для прохождения пути от точки 1 до точки 2 (Рис. 4.1.2), равно:

(4.1.58)

Рис. 4.1.2. К принципу Ферма

Имеющая размерность длины величина

(4.1.59)

называется оптической длиной пути . В однородной среде оптическая длина пути равна произведению геометрической длины пути на показатель преломления:

(4.1.60)

Следовательно,

(4.1.61)

Пропорциональность времени прохождения оптической длине пути дает возможность сформулировать принцип Ферма так: свет распространяется по такому пути, оптическая длина которого минимальна.

Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален при движении света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении.

Получим с помощью принципа Ферма законы отражения и преломления света. Пусть свет попадает из точки А в точку В, отразившись от поверхности MN (Рис. 4.1.3).

Рис. 4.1.3. Закон отражения света как следствие принципа Ферма

Прямой путь из А в В прегражден экраном Э. Среда, в которой распространяется луч, однородна, поэтому минимальность оптической длины пути сводится к минимальности геометрической длины пути. Геометрическая длина произвольно взятого пути равна АО’B = A’O’B, поскольку вспомогательная точка A’ является зеркальным отражением точки А, и АО’ = A’O’. Из Рис. 4.1.3 видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. При удалении точки O’ от точки О геометрическая длина пути неограниченно возрастает, что противоречит принципу Ферма. Этот результат можно записать так:

(4.1.62)

Соотношение (4.1.62) выражает закон отражения света : отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения.

Найдем точку, в которой должен преломиться луч, распространяясь от А к В, чтобы оптическая длина пути была минимальной (Рис. 4.1.4).

Рис. 4.1.4. К расчету закона преломления света из принципа Ферма

Для произвольного луча оптическая длина пути равна:

(4.1.63)

Чтобы найти минимальное значение оптической длины пути, продифференцируем L по х и приравняем производную к нулю:

(4.1.64)

Множители при n₁ и n₂ равны, соответственно, sinθ и sinθ». Поэтому получаем соотношение:

(4.1.65)

которое выражает закон преломления света. Используя взаимосвязь показателей преломления с фазовыми скоростями распространения света в средах, можно записать соотношение (4.1.65) в виде:

(4.1.66)

Следовательно, закон преломления света гласит: преломленный луч лежит в одной плоскости с падающим лучом и нормалью; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ.

В (4.1.66) n₁₂ — относительный показатель преломления второго вещества по отношению к первому. Из (4.1.65) видно, что при переходе света из оптически более плотной среды в оптически менее плотную луч удаляется от нормали к поверхности раздела сред. Увеличение угла падения сопровождается более быстрым ростом угла преломления, и при достижении некоторого предельного угла падения угол преломления будет равным 90°:

(4.1.67)

Отсюда:

(4.1.68)

При углах падения, лежащих в пределах от θ_пред пред до 90°, преломленной волны не существует, вся энергия падающей волны переходит в энергию отраженной волны. Это явление называется полным внутренним отражением.

Показатели преломления некоторых веществ при λ=0,589 мкм

Вещество	Показатель преломления	Вещество	Показатель преломления
Воздух	1,0003	Стекло (крон)	1,515
Вода	1,333	Стекло (флинт)	1,752
Спирт (этиловый)	1,362	Алмаз	2,420

Во многих оптических приборах для преломления света используются стеклянные призмы. На Рис. 4.1.5 показан ход луча монохроматического света в призме.

Рис. 4.1.5. Ход лучей в призме

После двукратного преломления луч оказывается отклоненным от первоначального положения на угол δ ( угол отклонения ). Угол θ, заключенный между преломляющими гранями, называется преломляющим углом . Угол δ зависит от преломляющего угла θ и показателя преломления призмы. Эта зависимость может быть легко показана для призмы с малым преломляющим углом θ (тонкой призмы) в случае малого угла падения α. Исходя из закона преломления и принимая значение показателя преломления воздуха равным единице, можно записать:

(4.1.69)

При малых углах α и θ углы α₁, γ и γ₁ также малы. Поэтому вместо (4.1.69) можно приближенно записать:

(4.1.70)

Из четырехугольника BQDE, в котором углы при В и D — прямые, найдем, что угол BED равен 180° — θ. Тогда из четырехугольника BСDE находим:

(4.1.71)

Отсюда

(4.1.72)

Угол δ из треугольника BED равен:

(4.1.73)

Подставляя в (4.1.72) результаты (4.1.73) и (4.1.70), получим окончательно:

(4.1.74)

4.1.6. Преломление в линзе

В практических применениях большое значение имеет преломление света на сферической границе раздела двух сред. Основная деталь оптических приборов — линза — обычно представляет собой стеклянное тело, ограниченное с двух сторон сферическими поверхностями. В частном случае одна из поверхностей линзы может быть плоской. Такую поверхность можно рассматривать как сферическую с бесконечно большим радиусом кривизны.

Линзы могут быть изготовлены не только из стекла, а из любого прозрачного вещества с показателем преломления, превышающим единицу, например, из кварца, каменной соли, пластмасс и других материалов. Поверхности линз могут быть и более сложной формы — цилиндрические, параболические и т.д.

Рассмотрим линзу, ограниченную двумя сферическими преломляющими поверхностями PO₁Q и PO₂Q (Рис. 4.1.6).

Рис. 4.1.6. Тонкая линза

Центр первой преломляющей поверхности PO₁Q лежит в точке С₁, центр второй поверхности PO₂Q — в точке С₂. Будем считать, что расстояние O₁O₂ мало по сравнению с O₁С₁ или O₂С₂. В таком случае точки O₁ и O₂ можно считать практически совпадающими с точкой О — оптического центра линзы. Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей, называется главной оптической осью , остальные — побочными осями .

Луч, идущий по какой-либо оптической оси, проходя через тонкую линзу, не меняет своего направления. Лучи, идущие параллельно главной оптической оси, после преломления в линзе пересекаются в одной точке F, расположенной на главной оптической оси и называемой главным фокусом .

Покажем, что лучи, исходящие под небольшими углами α из некоторой точки А, лежащей на главной оптической оси, собираются линзой в одну точку А₁, расположенную также на этой оптической оси и называемую изображением точки А (Рис. 4.1.7).

Рис. 4.1.7. Преломление в тонкой линзе

Построим плоскости, касательные к поверхностям линзы в точках М и N (в местах падения луча на линзу и его выхода из линзы), и проведем в эти точки радиусы R₁ и R₂ кривизны поверхностей линзы. Тогда луч AMNA₁ можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом θ. Учитывая малость углов α, β, α₁, β₁ и толщины линзы, можно записать:

(4.1.75)

где а и b — расстояния от источника света А и от его изображения А₁ до оптического центра линзы.

Из треугольников АНА₁ и ВЕВ₁ следует, что:

(4.1.76)

Принимая во внимание формулы (4.1.75), получим:

(4.1.77)

Учтено, что для тонкой линзы h₁ ≈ h₂ ≈ h. Поскольку, согласно формуле (4.1.74) для тонкой призмы выполняется: θ = (n-1)δ, то, с помощью (4.1.77) имеем формулу линзы :

(4.1.78)

В эту формулу не входит величина h, что означает, что расстояние b не зависит от от положения точки М. Следовательно, все лучи, исходящие из точки А, соберутся после преломления разными частями линзы в одной точке А₁ .

Если точка А находится бесконечно далеко от линзы (а = ∞), т.е. если лучи падают на линзу параллельно главной оптической оси, то, согласно формуле (4.1.78), имеем:

(4.1.79)

Величина b = f называется фокусным расстоянием линзы :

(4.1.80)

Фокусом линзы называется точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.

Принимая во внимание (4.1.80), формулу линзы (4.1.78) можно сейчас переписать так:

(4.1.81)

Величина, обратная фокусному расстоянию, называется оптической силой линзы :

(4.1.82)

Оптическая сила выражается в диоптриях (дп). 1 дп — оптическая сила линзы с фокусным расстоянием в 1 м.

4.1.7. Принцип Гюйгенса

В приближении геометрической оптики свет за преградой не должен проникать в область геометрической тени. В действительности световая волна распространяется во всем пространстве за преградой, проникая проникать в область геометрической тени, причем это проникновение будет тем более существенным, чем меньше размеры отверстия. При диаметре отверстия или ширине щели, сравнимых с длиной волны, приближение геометрической оптики становится совершенно неприменимым.

Качественно поведение света за преградой с отверстием может быть объяснено с помощью принципа Гюйгенса . Согласно принципу Гюйгенса каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент времени. Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (Рис. 4.1.8).

Рис. 4.1.8. К принципу Гюйгенса

Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн, можно убедиться в том, что за отверстием волна проникает в область геометрической тени, огибая края преграды.

4.1.8. Интерференция световых волн

Если в среде распространяются одновременно несколько электромагнитных волн, то волны просто накладываются друг на друга, не возмущая одна другую. Это утверждение, подкрепленное опытом, называется принципом суперпозиции.

В случае, когда колебания электрического и магнитного векторов в каждой из волн происходят так, что между соответственными векторами в разных волнах имеется постоянный во времени и в пространстве фазовый сдвиг, такие волны называются когерентными . Очевидно, что условие когерентности может существовать лишь для волн, которые имеют одинаковые частоты и, соответственно, длины волны.

При сложении когерентных волн возникает явление интерференции , заключающееся в том, что электромагнитные волны в одних точках пространства усиливают, а в других ослабляют друг друга.

Пусть две волны одинаковой частоты, распространяющиеся в одном направлении, возбуждают в некоторой точке пространства колебания:

(4.1.83)

Эти векторы можно представить как вращающиеся с частотой ω вокруг общего начала коор-динат. Поскольку сдвиг фаз различен, в какой-либо момент времени эти вектора займут различные положения (Рис. 4.1.9).

Рис. 4.1.9. К расчету интерференции волн

Используя теорему косинусов, получим амплитуду результирующего колебания:

(4.1.84)

Если сдвиг фаз между когерентными колебаниями равен нулю (волны — в фазе), то амплитуда результирующей волны максимальна и равна A = A₁ + A₂. Пусть амплитуды этих волн равны. В этом случае имеем амплитуду результирующей волны:

(4.1.85)

Если сдвиг фаз между когерентными колебаниями равен ±π (волны — в противофазе), то амплитуда результирующей волны минимальна и равна A = A₁ — A₂. Если амплитуды этих волн равны, то в этом случае они гасят друг друга:

(4.1.86)

Когерентные световые волны можно получить, разделив, например, с помощью зеркал волну, излучаемую одним источником, на две. Если заставить эти волны пройти разные пути, а затем наложить их друг на друга, будет наблюдаться интерференция. Пусть такое разделение происходит в точке О (Рис. 4.1.10).

Рис. 4.1.10. Образование когерентных волн

До точки Р первая волна пройдет в среде с показателем преломления n₁ путь S₁, вторая волна пройдет в среде с показателем преломления n₂ путь S₂. Если в точке О фаза колебания была равна ωt, то первая волна возбудит в точке Р колебание

(4.1.87)

а вторая волна — колебание

(4.1.88)

поскольку фазовые скорости волн в средах равны, соответственно: . Следовательно, разность фаз волн в точке Р будет равна:

(4.1.89)

Поскольку выполняется:

(4.1.90)

то, подставляя (4.1.90) в (4.1.8), для сдвига фаз имеем выражение:

(4.1.91)

где

(4.1.92)

есть величина, называемая оптической разностью хода и равная разности оптических длин проходимых волнами путей в средах с различными показателями преломления.

Из (4.1.91) следует, что если оптическая разность хода равна целому числу длин волн в вакууме:

(4.1.93)

то разность фаз оказывается кратной 2π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в фазе. Следовательно, (4.1.93) является условием интерференционного максимума.

Если Δ равна полуцелому числу длин волн в вакууме:

(4.1.94)

то разность фаз оказывается равной δ = ±(2m + 1)π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в противофазе. Следовательно, (4.1.94) является условием интерференционного минимума.

4.1.9. Дифракция световых волн

Дифракцией называется совокупность явлений, связанных с отклонениями от законов геометрической оптики. В частности, вследствие дифракции происходит огибание световыми волнами препятствий и проникновение света в область геометрической тени.

Между интерференцией и дифракцией нет существенного физического различия.

Свет, идущий от небольшого яркого источника через круглое отверстие (Рис. 4.1.11) должен по правилам геометрической оптики дать на экране резко ограниченный светлый кружок на темном фоне.

Рис. 4.1.11. Дифракция от круглого отверстия

Такая картина наблюдается при обычных условиях опыта. Но если расстояние от отверстия до экрана в несколько тысяч раз превосходит размеры отверстия, то образуется более сложная картина, которая состоит из совокупности светлых и темных концентрических колец.

Интересный случай дифракции осуществляется с помощью дифракционной решетки, которая представляет собой пластинку, на поверхности которой чередуются узкие параллельные прозрачные и непрозрачные полоски. Сумму ширины прозрачной и непрозрачной полосок называют периодом решетки. Пусть на решетку падает монохроматический свет с длиной волны λ (Рис. 4.1.12). Фронт волны параллелен плоскости решетки.

Рис. 4.1.12. Дифракционная решетка

Разности хода лучей, идущих от соответствующих точек отверстий, например от правых краев (точки А, А₁, А₂, . ), или от левых краев (точки В, В₁, В₂, . ) имеют одно и то же значение:

Для того, чтобы все пучки усиливали друг друга, необходимо, чтобы разность хода равнялась целому числу длин волн:

(4.1.95)

где m — целое число.

Это условие позволяет определить те значения углов φ и соответствующие направления, в которых будут наблюдаться максимумы света длины волны λ.

Для данной длины волны может наблюдаться несколько максимумов. Направление, соответствующее m = 0, есть φ = 0. Это — направление первоначального пучка. Соответствущий максимум носит название максимума нулевого порядка. При m = 1 имеем: sinφ₁ = λ/d, при m = –1 имеем: sinφ’₁ = –λ/d, т.е. имеется два максимума первого порядка, расположенных симметрично по обеим сторонам от нулевого максимума. Аналогично располагаются максимумы второго, третьего и т.д. порядков.

Отсюда следует, что для волн разной длины λ положения максимумов нулевого порядка совпадают , а положения максимумов первого, второго и т.д. порядков различны: чем больше λ, тем больше соответствующие углы.

Если на решетку падает белый свет, то в плоскости экрана получается ряд цветных изображений щели. На месте нулевого максимума будет изображение щели в белом свете, а по обе стороны от него развернутся цветные полосы от фиолетового к красному концу.

Чем больше общий размер решетки, т.е. чем больше полосок она содержит, тем выше ее качество: увеличение числа полосок увеличивает количество пропускаемого решеткой света (максимумы становятся ярче), и улучшает разрешение близких волн (максимумы становятся резче).

Зная период дифракционной решетки, ее можно использовать для определения длины световой волны, измерив величину угла φ, определяющего положение максимума данного порядка. В этом случае имеем:

(4.1.96)

Измерение длины световой волны с помощью дифракционной решетки принадлежит к числу наиболее точных методов.

4.1.10. Поляризация световых волн

Поляризованным называется свет, в котором направления колебаний электрического и магнитного векторов упорядочены каким-либо образом. В естественном свете колебания происходят в различных направлениях, быстро и беспорядочно сменяя друг друга.

Различают свет эллиптически поляризованный, поляризованный по кругу, плоскополяризованный. В случае эллиптической или круговой поляризаций электрический и магнитный векторы вращаются в пространстве с частотой, равной частоте волны, причем концы этих векторов описывают либо эллипс, либо круг. Вращение может происходить как по, так и против часовой стрелки. Если вектор вращается в пространстве как правый винт, то поляризацию называют правой, и левой — если вектор вращается в пространстве как левый винт.

Важный частный случай — плоская поляризация. В этом случае вектор электрического поля колеблется в плоскости, проходящей через направление распространения волны и этот вектор. Такую плоскость называют плоскостью колебаний . Вектор магнитного поля колеблется в плоскости, также проходящей через направление распространения волны и этот вектор, но данная плоскость — плоскость поляризации — составляет с плоскостью колебаний прямой угол (Рис. 4.1.13).

Рис. 4.1.13. Структура плоскополяризованной световой волны

Плоскополяризованный свет можно получить из естественного с помощью устройств, которые называются поляризаторами . Эти устройства свободно пропускают волны с колебаниями, плоскость которых совпадает с плоскостью пропускания поляризатора, и задерживают все другие волны.

Пусть на поляризатор падает плоскополяризованный свет амплитуды А₀ и интенсивности I₀. Сквозь устройство пройдет составляющая колебания с амплитудой А_|| = А₀cosφ, где угол φ — угол между плоскостью колебаний падающего света и плоскостью пропускания поляризатора (Рис. 4.1.14).

Рис. 4.1.14. Прохождение плоскополяризованного света через поляризатор

Следовательно, интенсивность прошедшего света определяется выражением:

(4.1.97)

Это соотношение носит название закона Малюса.

Пусть на пути естественного луча стоят два поляризатора, плоскости пропускания которых составляют угол φ. Из первого поляризатора выйдет плоскополяризованный свет, интенсивность которого I0 составит половину интенсивности естественного неполяризованного света I_ест. Используя закон Малюса, получаем:

(4.1.98)

Максимальная интенсивность получается при φ = 0 (плоскости пропускания поляризаторов параллельны). При φ = 90° интенсивность равна нулю — скрещенные поляризаторы не пропускают свет.

4.1.11. Вращение плоскости
поляризации световых волн

Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через них плоскополяризованного света. К числу таких веществ относятся кристаллы кварц, киноварь и др, некоторые жидкости (скипидар, никотин), растворы оптически активных веществ в оптически неактивных растворителях (водные растворы сахара, винной кислоты и др.)

Угол поворота плоскости поляризации в твердых веществах пропорционален пути l, пройденному лучом в кристалле:

(4.1.99)

где α — постоянная оптического вращения, различная для разных веществ.

В растворах угол поворота плоскости поляризации пропорционален пути l, пройденному светом в растворе и концентрации с активного вещества:

(4.1.100)

Здесь [α] — удельная постоянная вращения.

В зависимости от направления вращения вещества подразделяются на право- и левовращающие. Существуют правый и левый кварц, правый и левый сахар и т.д. Молекулы или кристаллы одной модификации являются зеркальным отражением молекул или кристаллов другой модификации.

Если между двумя скрещенными поляризаторами поместить оптически активное вещество, то поле зрения просветляется. Чтобы снова затемнить его, надо повернуть один из поляризаторов на угол, определяемый соотношениями (4.1.99) или (4.11.100). Таким методом можно измерить концентрацию активного вещества в растворе, в частности, концентрацию сахара.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2015

Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:

🔍 Видео