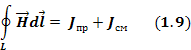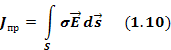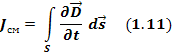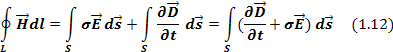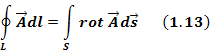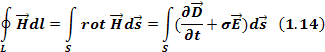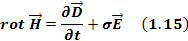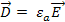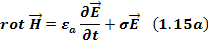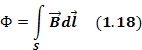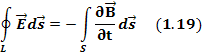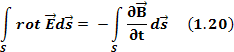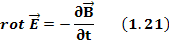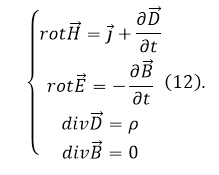Уравнение максвелла обобщение закона полного тока (7 видео)

Первое уравнение Максвелла.

Первое уравнение Максвелла — это обобщение закона Ампера и Био-Саварра для токов смещения. Звучит следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур.

В современном обозначении записывается

Т.о. физический смысл первого уравнения Максвелла состоит в том, что магнитное поле в некоторой области пространства связано не только с токами проводимости, протекающими в этой области, но и с изменением электрического поля во времени в этой области(токами смещения).

Это означает, что циркуляция вектора 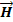по контуру L равна сумме токов проводимости и смещения.

Подставляя 1.10, 1.11 в 1.9, получим

Уравнение 1.12 называют первым уравнением Максвелла в интегральной форме.

Получим дифференциальную форму уравнения Максвелла. Для этого воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:

Применим уравнение 1.13 к левой части уравнения 1.12. Получим

Уравнение 1.14 справедливо, если равны подынтегральные функции, то есть

Уравнение 1.15 есть первое уравнение Максвелла в дифференциальной форме.

Для изотропных сред

Подставим в 1.15

Дифференциальная форма первого уравнения Максвелла используется в том случае, когда производные поля по координатам пространства непрерывны. Интегральная форма 1.12 такого ограничения не имеет.

§1.3. Второе уравнение Максвелла.

Второе уравнение Максвелла— это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве

где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС. ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.

(1.17)

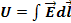
Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. То есть переменное магнитное поле возбуждает вихревое электрическое поле.

Получим второе уравнение Максвелла в интегральной форме

Уравнение 1.19 – второе уравнение Максвелла в интегральной форме.

Воспользуемся уравнением Стокса 1.13, преобразуем левую часть уравнения 1.19:

Уравнение 1.20 есть второе уравнение Максвелла в дифференциальной форме.

Содержание

4.1. Обобщение Максвеллом закона полного тока. Гипотеза о токе смещения
Уравнения Максвелла как обобщение экспериментальных данных
Готовые работы на аналогичную тему
💥 Видео

Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

4.1. Обобщение Максвеллом закона полного тока. Гипотеза о токе смещения

Физика девятнадцатого столетия ознаменовалась открытием законов электромагнетизма и установлением возможности взаимных переходов электрического тока и магнитного поля. Законы этих переходов связывают электрический ток с магнитным полем, но не содержат характеристик электрического поля, хотя хорошо известно, что существование тока без последнего невозможно.

Законы, выражающие связь магнитных полей с электрическим током зависят от формы того проводника, по которому течет ток, т. е. лишены общности. Закон полного тока (3.31) в этом смысле выделяется из них, выражает свойство непотенциальности магнитного поля, поэтому может быть признан за один из фундаментальных законов. Но и он свидетельствует о возможности создать магнитное поле лишь вблизи проводника. В диэлектрике нет зарядов, способных свободно перемещаться, поэтому в них невозможно создать ток, следовательно, не может существовать и магнитное поле. Максвеллу такая ситуация представилась нелогичной: поле не связано непосредственно с проводником, значит, его возникновение не должно зависеть от среды. Более того, само направленное движение возможно лишь при наличии электрического поля , для которого среда не должна служить препятствием.

Внимательный взгляд на хорошо известную нам теорему Гаусса (2.13) подтверждает эту мысль: используемое в ней понятие потока вектора напряжённости приложимо только к полю.

Поток через замкнутую поверхность S, согласно этой теореме, связан с зарядом, создающим поле. Поэтому, используя определение потока (2.13), упомянутую теорему можно записать иначе, выразив заряд, создающий поле, через напряжённость:

Уравнение максвелла обобщение закона полного тока

(4.1)

если напряжённость во всех точках поверхности одинакова и перпендикулярна поверхности. Из определения силы тока и последнего равенства получаем

(4.2)

то есть сила тока через поверхность S пропорциональна скорости изменения напряжённости электрического поля.

Оказывается, что ток не обязательно связан с зарядом. Он может создаваться также изменяющимся во времени электрическим полем. Этот ток Максвелл назвал током смещения. В отличие от тока проводимости он может существовать и в вакууме, и в диэлектрике. Но так же, как и обычный ток, он должен создавать магнитное поле. Если не допускать существования тока смещения, то цепь оказывается разомкнутой, как только в нее вставить конденсатор. В самом деле, между обкладками конденсатора содержится диэлектрик, и ток по нему протекать не может. Это имеет место для случая, когда по цепи течет постоянный ток. Для этого случая и поле постоянно, то есть производная от E по t равна нулю. Для переменного тока величина напряжённости меняется, и производная отлична от нуля. По диэлектрику между обкладками конденсатора потечет ток смещения, цепь замкнется, несмотря на наличие диэлектрика. Тот факт, что переменный ток течет по цепи, содержащей конденсаторы, известен всем, кто имеет дело с электрическими цепями. Исторически ток смещения был впервые обнаружен Эйхенвальдом в 1901 году в Петербурге по его действию на магнитную стрелку, подвешенную над конденсатором, к которому подводилось переменное напряжение высокой частоты (рис.

Высказанное предположение о возможности существования тока в диэлектрике получило название первой Максвелловской гипотезы, которая была таковой вплоть до 1901 года, то есть почти полвека. Выражение (4.2) есть математическая формулировка этой гипотезы.

Итак, если воспользоваться гипотезой о существовании тока смещения, закон полного тока (3.31) можно записать в виде

(4.3)

Полученное уравнение является обобщенным законом, поскольку использует гипотезу о токе смещения и имеет место в любой среде, а не только там, где протекает ток. Более того, в уравнении мы впервые встречаемся с непосредственной связью двух полей — электрического и магнитного, с фактом возможности перехода одного поля в другое. Нетрудно, пользуясь понятием циркуляции вектора (1.8), показать, что изменение вектора во времени приводит к появлению не постоянного, а переменного по координате магнитного поля .

Для того, чтобы использовать понятие циркуляции вектора , рассмотрим рис. 4.2. Начиная обход по контуру, помним, что начинать его лучше из точки, ближайшей к началу координат. Помним также, что проекция имеет положительный знак, если направление обхода совпадает с направлением оси!

На рис. 4.2 изображена система координат с тремя осями, показан ток i, текущий по оси z и силовая линия магнитного поля, лежащая в плоскости xoy и проходящая через точку A. В этой же плоскости изображен контур со сторонами dx и dy и показаны проекции на эти стороны вектора , касательного к силовой линии.

Обратите внимание, что проекций у вектора только две, то есть мы будем рассматривать лишь двумерный случай:

(4.4)

где DS = DxDy — площадь контура.

Предлагаем читателю, пользуясь (1.7), получить это уравнение непосредственно из чертежа. Заменив полученным уравнением круговой интеграл в обобщённом законе полного тока (4.3), получим первое уравнение Максвелла:

(4.5)

Уравнение является обобщением закона полного тока и содержит утверждение, что меняющееся по времени электрическое поле создаёт меняющееся по координате магнитное. Тот факт, что мы рассматриваем лишь упрощенный двумерный случай и не используем весь математический аппарат теории поля, делает это уравнение по внешнему виду несколько отличным от того, который обычно приводится в учебниках.

Видео:3 14 Уравнения МаксвеллаСкачать

Уравнения Максвелла как обобщение экспериментальных данных

Вы будете перенаправлены на Автор24

Основой электродинамики в неподвижных средах является система уравнений Дж Максвелла. Эти уравнения получены последовательной систематизацией, интеграцией и исследованием эмпирических фактов. Прежде всего, необходимо решить, какие из известных ранее уравнений могут быть оставлены без изменений и оговорок, какие из них требуют обобщения, трансформации или вообще требуется отбросить. В качестве ориентира в этом отношении используют следующее положение: исключаются из состава основных все уравнения, в основе которых лежат представления о непосредственном действии на расстоянии. К таким законам относят, например, закон Кулона, Био и Савара. Эти законы не совмещаются с пониманием того, что электромагнитные взаимодействия распространяются с конечной скоростью, следовательно, не являются верными в абсолютно всех случаях. Сохраняют только те уравнения, которые не противоречат положениям теории поля.

В качестве гипотезы предполагается, что теорема Остроградского — Гаусса:

уравнение:

закон электромагнитной индукции (в формулировке Максвелла):

являются общими законами электродинамики. То, что они удовлетворяют требованиям теории поля, следует из существования этих же законов в дифференциальной (полевой) трактовке:

К основным уравнениям электродинамики добавляют закон сохранения заряда, который в дифференциальной форме представлен как:

В случае стационарности электромагнитного поля выражение (5) переходит в:

Теорема о циркуляции:

может быть также записана в дифференциальной форме:

следовательно, удовлетворяет требованиям теории поля. Тем не менее, она не входит в состав основных уравнений электродинамики. Если в выражении (8) провести операцию дивергенции для обеих частей равенства, то получим, что $divoverrightarrow=0$, так как $div(rotoverrightarrow=0$. Однако, выражение (6) справедливо только для стационарных токов. Получается, что мы получено противоречие с уравнением (5) для общего случая. Полагать, что не выполняется закон (5) нельзя, так как это фундаментальный закон сохранения заряда. Значит, следует сделать вывод, что выражения (7) и (8) требуют обобщения. Это обобщение вводится в виде тока смещения. Плотность тока смещения ($overrightarrow<j_>$) определена как:

Готовые работы на аналогичную тему

Максвелл назвал плотностью полного тока выражение $ overrightarrow+overrightarrow<j_>$ , причем:

Максвелл переписал выражение (8) в виде:

Доказательством истинности уравнения (11) служат опытные данные, которые подтверждают уравнение (11).

Итак, Максвелл дополнил основные положения электромагнетизма введением токов смещения и написал систему фундаментальных уравнений электродинамики. В настоящее время их четыре. В дифференциальной форме эта система имеет вид:

В число фундаментальных уравнений не включено уравнение непрерывности (5), так как это уравнение — следствие уравнений, которые входят в систему Максвелла.

Уравнения Максвелла показывают, что источниками электрического поля служат электрические заряды и переменные магнитные поля. Магнитные поля порождаются перемещающимися электрическими зарядами (токами) и переменными электрическими полями. Уравнения Максвелла не являются симметричными относительно магнитного и электрического полей. Это произошло вследствие того, что электрические заряды в природе существуют, а магнитных зарядов считается, что не существует. Дирак, в свое время, стремясь придать уравнениям электродинамики симметрию, выдвинул гипотезу о существовании магнитных зарядов, назвал их единичными магнитными полюсами (монополиями). Логических противоречий этой гипотезе нет. Существование таких зарядов потребовало бы обобщения уравнений Максвелла. Потребовалось бы к источникам магнитного поля добавить магнитные заряды, а к источникам электрических полей — магнитные токи. При этом справедливость уравнений Максвелла была бы ограничена областями, в которых магнитных зарядов и магнитных токов нет. Однако попытки экспериментального обнаружения магнитных зарядов по сей день успехом не увенчались.

Рассуждения, с помощью которых получена система уравнений Максвелла, не может служить доказательством. Принципиально новые положения старая теория никогда не содержит. В этом смысле нельзя вывести уравнения Максвелла логически. Данные уравнения следует рассматривать как основные аксиомы электродинамики, которые получены путем обобщения эмпирических данных.

Задание: Объясните, в чем разница между пониманием явления электромагнитной индукции Максвеллом и Фарадеем?

Решение:

Согласно представлениям Фарадея, электромагнитная индукция состоит в том, что переменное магнитное поле возбуждает электрический ток. Для того чтобы наблюдать это явление, обязательно требуется замкнутый проводник.

Максвелл видел суть электромагнитной индукции прежде всего в порождении электрического поля, следовательно, это явление можно наблюдать, когда в пространстве нет проводников вообще. И возникновение электрического тока в проводнике — одно из проявлений электрического поля, которое появляется как следствие изменения магнитного поля. Это поле может выполнять и другие действия, например, поляризовать диэлектрик, ускорять заряженные частицы. Предположение Максвелла подтверждают эксперименты, которые показывают, что ЭДС индукции не зависит от рода и состояния проводника (его температуры, однородности). Это показывает, что причиной возникновения ЭДС заключается в появлении электрического поля под действием переменного магнитного поля, и проводник играет второстепенную роль и является детектором поля.

Важная особенность явления в том, что появляющееся электрическое поле не является электростатическим. Электрическое поле, которое появляется при электромагнитной индукции, имеет непрерывные линии напряженности (обладает вихревым характером). Циркуляция вектора напряженности в таком поле отлично от нуля зависит от формы проводящего контура. Углубленное истолкование явления электромагнитной индукции ведет к основному положению теории Максвелла о том, что переменное магнитное поле вызывает появление вихревого электрического поля. Что количественно отображается в уравнении:

Задание: Что представляет собой система уравнений Максвелла для стационарных полей?

Решение:

В том случае, если мы рассматриваем стационарное магнитное и стационарное электрическое поля, то следует учесть, что:

В таком случае, система уравнений Максвелла распадется на две группы независимых уравнений. Первая группа — уравнения электростатики:

[rotoverrightarrow=0, divoverrightarrow=rho left(2.2right).]

Вторая группа — уравнения магнитостатики:

[rotoverrightarrow=overrightarrow, divoverrightarrow=0 left(2.3right).]

В случае стационарных полей электрическое и магнитное поля независимы друг от друга. Источниками электрического поля являются только электрические заряды, источники магнитного поля — токи проводимости.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 03 2021