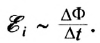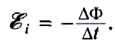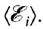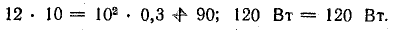Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.
Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):
- Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
- В дальнейшем он вызывает появление магнитного поля.
- Уравнения Максвелла в дифференциальной форме
- Уравнение 1: Закон Гаусса или Теорема Гаусса
- Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
- Уравнение 3: Закон Гаусса для магнетизма
- Уравнение 4: Закон Ампера
- Уравнения Максвелла в интегральной и дифференциальной форме
- Уравнение 1: Закон Гаусса (Теорема Гаусса)
- Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
- Уравнение 3: Закон Гаусса для магнетизма
- Уравнение 4: Закон Ампера
- Закон электромагнитной индукции — формулы и определение с примерами
- Электромагнитная индукция
- Закон электромагнитной индукции
- Наведение э.д.с. в проводнике, движущемся в магнитном поле
- Э.Д.С. Самоиндукции и взаимоиндукции
- Э.д.с. взаимоиндукции
- Электромагнитная индукция. Уравнения Максвелла для электромагнитного поля
- 🎬 Видео
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Уравнения Максвелла в дифференциальной форме
Уравнение 1: Закон Гаусса или Теорема Гаусса
Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.
Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.
Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.
Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.
Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
Можно создать электрическое поле, изменив магнитное поле.
Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:
- Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
- Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
- Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.
Уравнение 3: Закон Гаусса для магнетизма
Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.
Закон Гаусса для магнетизма утверждает (очень кратко):
- Магнитных монополей не существует.
- Расхождение полей B или H всегда равно нулю в любом объёме.
- На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.
Уравнение 4: Закон Ампера
Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.
Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Уравнения Максвелла в интегральной и дифференциальной форме
Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.
Уравнение 1: Закон Гаусса (Теорема Гаусса)
Это же уравнение в интегральной форме:
Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
И это же уравнение в интегральной форме:
Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.
Уравнение 3: Закон Гаусса для магнетизма
И это же уравнение в интегральной форме:
Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.
Уравнение 4: Закон Ампера
И это же уравнение в интегральной форме:
Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Закон электромагнитной индукции — формулы и определение с примерами
Закон электромагнитной индукции:
Вам уже известно, что электрический ток, или движущиеся заряды, создают в окружающем пространстве магнитное поле. А возможен ли обратный процесс, при котором с помощью магнитного поля в замкнутом проводнике будет создан электрический ток?
Именно такой вопрос заинтересовал выдающегося английского физика Майкла Фарадея, который в 1821 г. в своем дневнике поставил перед собой задачу: «Превратить магнетизм в электричество». Через 10 лет упорного труда эта задача была им успешно решена. В августе 1831 г. Фарадей сделал фундаментальное открытие в области электромагнитных явлений.
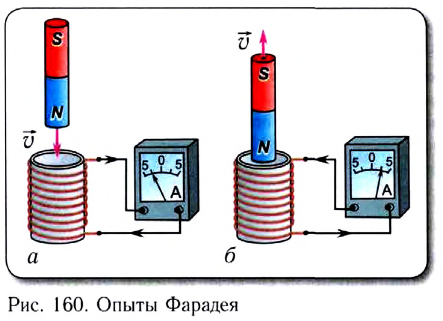
При проведении опытов Фарадей обнаружил, что при введении постоянного магнита в катушку (рис. 160, а) или при выведении из нее (рис. 160, б) стрелка гальванометра в цепи катушки отклонялась, т. е. в цепи возникал кратковременный электрический ток. Изменение направления движения магнита приводило к отклонению стрелки гальванометра в противоположную сторону (см. рис. 160).
Таким образом, при изменении индукции магнитного поля, пронизывающей витки катушки, в замкнутой цепи возникает электрический ток, называемый индукционным. Следовательно, в цепи появился источник тока. Можно сделать вывод о том, что изменение индукции магнитного поля в пределах площади, ограниченной контуром, приводит к появлению в контуре ЭДС, называемой электродвижущей силой индукции.
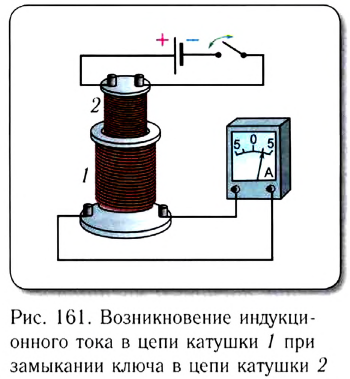
Фарадей наблюдал возникновение индукционного тока в цепи исследуемой катушки 1 не только при перемещении постоянного магнита, но и в том случае, если замыкали (размыкали) ключ в цепи, содержащей катушку 2, расположенную внутри катушки 1 (рис. 161 ).
Индукционный ток возникал в катушке 1 также при перемещении контура с током 2 в непосредственной близости от исследуемой катушки.
Таким образом, в результате серии экспериментов Фарадей установил, что возникновение индукционного тока в замкнутом контуре достигается при изменении магнитного потока через него.
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Эксперименты Фарадея позволили установить закон электромагнитной индукции (закон Фарадея), количественно определяющий ЭДС индукции в контуре:
- ЭДС электромагнитной индукции
возникающая в замкнутом контуре, прямо пропорциональна скорости изменения магнитного потока через него:
Как видно из приведенного соотношения, ЭДС индукции не зависит от материала проводника, его сопротивления, температуры и от носителей тока, а определяется только характером изменения магнитного поля.
Для объяснения возникновения ЭДС в неподвижном замкнутом контуре при изменении магнитного поля внутри него английский ученый Джеймс Клерк Максвелл предложил такую гипотезу: изменяющееся магнитное поле создает в окружающем пространстве электрическое поле, которое и приводит свободные заряды проводника в движение, т. е. создает индукционный ток. На основе этой гипотезы Максвелл создал теорию электромагнитного поля, подтвердившуюся на опыте. Согласно этой теории при изменении магнитного поля в некоторой области пространства обязательно возникает электрическое поле с замкнутыми силовыми линиями. Причем это происходит даже при отсутствии проводящего контура, например в вакууме.
Таким образом, явление электромагнитной индукции в более широком понимании заключается нс только в возникновении индукционного тока, или ЭДС индукции 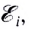
Русский физик Эмилий Ленц в 1833 г. сформулировал правило (правило Ленца), позволяющее установить направление индукционного тока в цепи:
возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
Согласно этому правилу в формуле, выражающей закон Фарадея, следует ставить знак «минус».
Максвелл в 1873 г. дал современную формулировку закона электромагнитной индукции:
- ЭДС индукции в замкнутом проводящем контуре равна скорости изменения пронизывающего его магнитного потока, взятой с противоположным знаком:
Знак «минус» в законе электромагнитной индукции (в формуле для 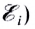
Отметим, что в таком виде закон применим только, когда скорость изменения магнитного потока постоянна. В общем случае эта формула дает среднее значение ЭДС индукции
Покажем, что если бы правило Ленца не выполнялось, то взаимодействие индукционного тока с внешними полями приводило бы к неограниченному росту энергии системы без подвода ее извне, т. е. к нарушению закона сохранения энергии.
Действительно, ток, возникающий за счет ЭДС индукции, сам является источником магнитного поля. Если бы индуцированное магнитное поле «помогало» расти магнитному потоку через контур, то тем самым увеличивался бы индукционный ток, что вызывало бы еще большее увеличение первоначального магнитного поля. Это сопровождалось бы еще большим изменением магнитного потока через контур, и так до бесконечности.
В результате сила индукционного тока и связанная с ним энергия возрастали бы неограниченно, что является нарушением закона сохранения энергии.
Для наглядной демонстрации правила Ленца используется прибор, состоящий из двух колец (замкнутого и незамкнутого), уравновешенных для уменьшения трения на игольчатой опоре (рис. 162).
При введении постоянного магнита в замкнутое кольцо оно «уходит» от него, а при выведении — «догоняет» магнит. Разрезанное кольцо никак не «реагирует» на движения магнита, поскольку в нем не может возникнуть индукционный ток.
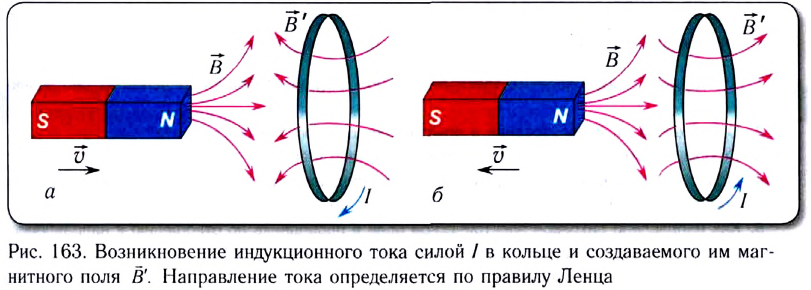
Рассмотрим более подробно движение постоянного магнита вблизи проводящего кольца.
При движении магнита вправо магнитный поток через кольцо увеличивается (рис. 163, а). В соответствии с правилом Ленца индукционный ток силой I создает магнитное поле 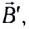
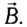
Движение магнита влево приводит к уменьшению магнитного потока через кольцо. Возникающий индукционный ток силой I создает поле 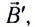
щее изменению начального магнитного потока, т. е. стремится сохранить начальную величину магнитного потока (рис. 163, б).
Таким образом, замкнутый контур как бы «сопротивляется» изменению пронизывающего его магнитного потока. Следовательно, возникновение индукционного тока можно рассматривать как проявление инерции системы.
В то же время возникновение индукционного тока в замкнутом контуре при изменении магнитного потока через него означает, что заряженные частицы пришли в движение под действием каких-то сил. Это не могут быть силы Лоренца, поскольку они действуют только на движущиеся заряды. Какие же силы заставляют двигаться электроны в покоящемся проводнике при изменении индукции магнитного поля?
Эти силы имеют электрическую природу, но по своим свойствам отличаются от электростатических сил (сил Кулона). При электромагнитной индукции возникает вихревое электрическое поле, действующее на заряженные частицы.
В отличие от потенциального электростатического поля, создаваемого неподвижными электрическими зарядами, вихревое электрическое поле, возникающее вследствие изменения магнитного поля, непотенциально. Это означает, что работа сил этого поля по замкнутой траектории не равна нулю, и они являются сторонними силами в замкнутом контуре при возникновении индукционного тока. Следовательно, работа сил вихревого электрического поля по перемещению единичного заряда по замкнутому контуру определяет ЭДС электромагнитной индукции.
Подчеркнем, что вихревое электрическое поле, возникающее при изменении магнитного поля, существует независимо от того, имеется или нет в этом месте замкнутый проводящий контур. Проводящий контур является лишь своеобразным индикатором, обнаруживающим наличие этого вихревого поля.
В отличие от электростатического вихревое электрическое поле имеет замкнутые силовые линии. Это связано с тем, что источниками электростатического поля являются электрические заряды, а источником вихревого электрического поля — переменное во времени магнитное поле.
Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами. В соответствии с законом Джоуля — Ленца они приводят к нагреванию проводников (выделению теплоты) и переходу энергии системы во внутреннюю энергию. Токи Фуко эффективно используются на практике: в плавильных печах, в установках для закалки металлических деталей, в сушильных установках, в медицине.
Открытие Фарадеем явления электромагнитной индукции позволило создать мощные генераторы электрического тока и положило начало промышленному производству электроэнергии, без которой невозможно представить существование современного общества.
Видео:60. Уравнения МаксвеллаСкачать

Электромагнитная индукция
Электромагнитная индукция — это одно из явлений, на которых основаны электротехника и радиотехника.
Для оценки важности этого явления достаточно назвать взаимное преобразование механической и электрической энергии, передачу и распределение электрической энергии, передачу и прием информации.
Знание явления и закона электромагнитной индукции необходимо при изучении электрических цепей переменного тока.
Закон электромагнитной индукции
Явление электромагнитной индукции открыл в 1831 г. английский физик М. Фарадей и на основе этого открытия сформулировал один из важнейших физических законов — закон электромагнитной индукции.
Явление электромагнитной индукции
Явление электромагнитной индукции можно продемонстрировать следующими опытами. Внутрь цилиндрической катушки, концы которой соединены с гальванометром, с определенной скоростью вводится постоянный магнит. Стрелка гальванометра отклоняется, обнаруживая электрический ток в катушке (рис. 10.1, а). При удалении магнита от катушки стрелка гальванометра отклоняется в обратную сторону.
Гальванометр обнаруживает ток в катушке, если перемещать ее относительно другой катушки с током, которую назовем первичной (рис. 10.1, б). На рис. 10.1, в показаны две катушки, расположенные на одном сердечнике. Одна из них присоединена к источнику электрической энергии через ключ, вторая замкнута через гальванометр.
Электрические катушки между собой не связаны, но при замыкании ключа наблюдается отклонение стрелки гальванометра в одну сторону, при размыкании — в другую.
Несмотря на внешнее различие опытов, их одинаковый результат дает основание полагать, что непосредственная причина возникновения электрического тока в цепи вторичной катушки в этих опытах одинакова.
Действительно, во всех рассмотренных опытах изменяется потокосцепление вторичной катушки: в первых двух случаях — благодаря изменению положения ее в магнитном поле, в третьем случае — в связи с увеличением тока в первичной катушке после замыкания ключа и уменьшением его после размыкания.
Возбуждение электродвижущей силы в контуре при изменении потокосцепления этого контура называется электромагнитной индукцией.
Под действием индуктированной э.д.с. в замкнутом контуре возникает индуктированный электрический ток. Возникновение тока означает, что во вторичный контур передается энергия, которая при наличии сопротивления в цепи превращается в тепло. В первых двух опытах электрическая энергия возникла за счет механической работы при перемещении постоянного магнита (рис. 10.1, а) или катушки (рис. 10.1, б). В третьем опыте обе катушки неподвижны, т. е. механическая работа не совершается. Электрическая энергия во вторичной катушке возникает за счет энергии источника, включенного в цепи первичной катушки. В этом случае электрическая энергия передается из одной цепи в другую посредством магнитного поля. 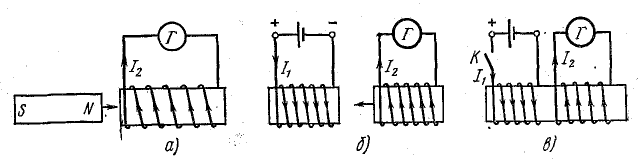
Рис. 10.1. Опыты для наблюдения электромагнитной индукции
Преобразование энергии из одного вида в другой посредством магнитного поля или изменение энергии поля количественно определяются через абсолютное значение изменения потокосцепления. Явление электромагнитной индукции, сопровождающее эти процессы, связано со скоростью изменения потокосцепления.
Закон электромагнитной индукции
Закон электромагнитной индукции устанавливает количественное выражение для индуктированной э. д. с.
Электродвижущая сила, индуктируемая в замкнутом контуре при изменении сцепленного с ним магнитного потока, равна скорости изменения потокосцепления, взятой с отрицательным знаком: 
В этой форме закон электромагнитной индукции был дан Максвеллом.
В катушке, имеющей несколько витков, общая э. д. с. зависит от числа витков N. Если все витки катушки сцеплены с одинаковым магнитным потоком, то э. д. с. будет в N раз больше: 
В общем случае витки катушки могут быть сцеплены с разными потоками, тогда ее общая э. д. с. определяется алгебраической суммой э. д. с. отдельных витков: 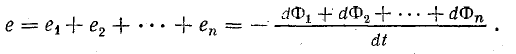
В числителе последнего выражения дана алгебраическая сумма изменений потокосцепления отдельных витков катушек, т. е. изменение общего потокосцепления.
Таким образом, э. д. с. катушки определяется скоростью изменения ее общего потокосцепления и общая формула закона электромагнитной индукции имеет вид
Правило Ленца
В 1833 г. проф. Петербургского университета Э. X. Ленц установил общее правило для определения направления индуктированного тока и электромагнитных сил, возникающих в результате взаимодействия магнитного поля с индуктированным током.
Если магнитный поток, сцепленный с проводящим замкнутым контуром, изменяется, в контуре возникают явления электрического и механического характера, препятствующие изменению магнитного потока.
Рис. 10.2. Схемы, поясняющие правило Ленца
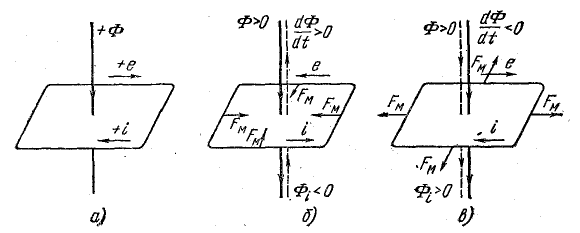
Правило Ленца отражает проявления электромагнитной инерции в системах контуров с токами. Этому правилу соответствует знак минус в формулах, выражающих закон электромагнитной индукции [см. (10.1) — (10.3)], если принять положительными направления магнитного потока и индуктированной в контуре э.д.с., удовлетворяющие правилу правого буравчика (рис. 10.2, а).
Предположим, что положительный магнитный поток, сцепленный с контуром, увеличивается. Приращение потока dФ и скорость его изменения dФ/dt положительны (dФ > 0, dФ/dt > 0). Индуктированная в контуре э. д. с., согласно правилу Ленца, направлена против выбранного положительного направления, т. е. отрицательна (е 0), т. е. совпадает с выбранным положительным направлением (рис. 10.2, в). Индуктированный в контуре ток i создает вторичный магнитный поток, совпадающий по направлению с основным потоком. Вторичный магнитный поток, возникновение которого можно рассматривать как реакцию системы контуров с токами на изменение ее магнитного состояния, в данном случае препятствует уменьшению основного магнитного потока. Возникающие при этом электромагнитные силы стремятся расширить контур с током, т. е. увеличить магнитный поток, сцепленный с ним.
Факторы, противодействующие изменению магнитного потока, тем сильнее, чем быстрее изменяется поток.
Электромагнитная инерция в системах контуров с токами подобна механической инерции в системах движущихся тел: при всяком изменении скорости возникают силы инерции, препятствующие этому изменению.
Задачи
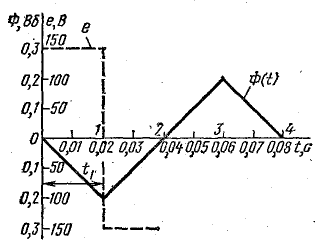
Задача 10.1. Магнитный поток, создаваемый током в катушке, изменяется по графику рис. 10.3. Построить график э. д. с., индуктированной в катушке с числом витков N = 15, если наибольшая величина потока Фm = 0,2 Вб.
Рис. 10.3. К задаче 10.1
Решение. Э. д. с: в катушке определяют по формуле (10.2), где dФ/dt — скорость изменения магнитного потока. На участке 0-1 отрицательный магнитный поток в течение t1 = 0,02 с растет от нуля до Фm = 0,2 Вб по линейному закону, поэтому скорость изменения потока постоянна и отрицательна: 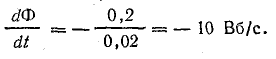
При постоянной скорости изменения магнитного потока э. д. с. будет постоянной: 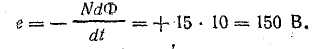
Знак э. д. с. определим по правилу Ленца.
Условно-положительные направления магнитного потока и индуктированной э. д. с. в катушке показаны на рис. 10.4, а.
На участке 0-1 кривой Ф(t) отрицательный магнитный поток увеличивается. Направления магнитного потока и тока в катушке, соответствующие этому отрезку времени, отмечены на рис. 10.4, б. Индуктированная э. д. с. препятствует росту магнитного потока, т. е. направлена против тока, создающего поток (пунктирные стрелки). В данном случае э. д. с. положительна, так как ее направление совпадает с условно-положительным направлением. 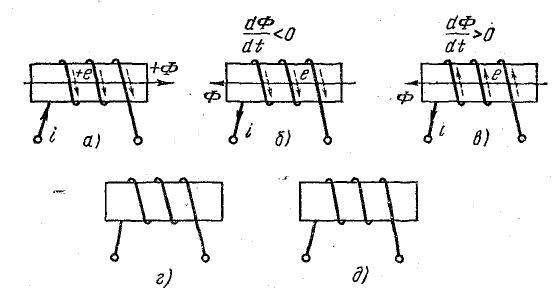
Рис. 10.4. К задаче 10.1
На участке 1-2 отрицательный магнитный поток уменьшается с той же скоростью, с какой он раньше увеличивался. Индуктированная э. д. с., сохраняя свою величину 150 В, препятствует уменьшению потока, т. е. направлена, так же как ток в катушке (рис. 10.4, в), против условно-положительного направления. Из формулы (10.2) также следует, что э. д. с. отрицательна.
Наведение э.д.с. в проводнике, движущемся в магнитном поле
В проводнике, движущемся в магнитном поле так, что он пересекает линии магнитной индукции, индуктируется электродвижущая сила. Это явление — разновидность электромагнитной индукции.
Выражение э.д.с. в проводнике, движущемся в магнитном поле
Рассмотрим отрезок АБ прямолинейного проводника, который движется, пересекая под прямым углом линии магнитной индукции равномерного поля с магнитной индукцией В.
На рис. 10.6, а показан проводник АБ, который катится в направлении механической силы Fмх по металлическим шинам, соединенным между собой через сопротивление R.
Проводник АБ, отрезки шин и сопротивление образуют замкнутый проводящий контур. При перемещении проводника на расстояние b с постоянной скоростью v магнитный поток, сцепленный с этим контуром, увеличивается за счет увеличения площади поверхности, ограниченной контуром.
Приращение магнитного потока 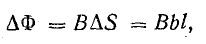
где l — длина части проводника АБ, находящейся в магнитном поле.
Абсолютная величина э. д. с. в контуре 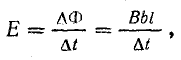
где Δt — время, в течение которого проводник АБ переместился на расстояние b; b/Δt = v — скорость движения проводника; поэтому
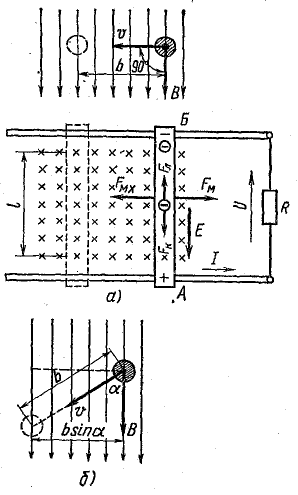
Рис. 10.6. Движение прямого провода в магнитном поле
Если проводник будет перемещаться под углом α 2 r = 12,8 Вт) и в приемнике (I 2 R = 115,2 Вт).
Задача 10.9. Устройство, описанное в задаче 10.8, переведено в режим двигателя. Для этого вместо приемника энергии в цепь включили аккумуляторную батарею с э. д. с. Е0 = 12 В и внутренним сопротивлением rа = 0,2 Ом.
Определить окружное усилие, вращающий момент и скорость рамки и составить баланс мощностей, если ток в цепи установился равным 10 А.
Решение. Определим э. д. с. в рамке согласно второму закону Кирхгофа: 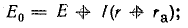
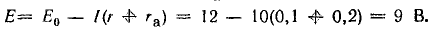
Линейная скорость вращения рамки 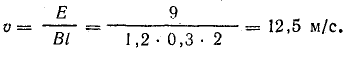
Частота вращения 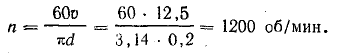
Окружное усилие на цилиндре 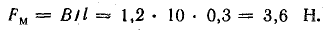
Вращающий момент 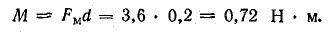
Механическая мощность 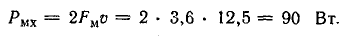
Баланс мощностей: мощность батареи равна сумме механической мощности и мощности потерь в электрической цепи: 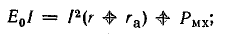
Э.Д.С. Самоиндукции и взаимоиндукции
При изменении собственного потокосцепления в контуре или катушке наводится э. д. с. самоиндукции eL, а при изменении взаимного потокосцепления — э. д. с. взаимоиндукции.
Э.д.с. самоиндукции
Изменение собственного потокосцепления обычно является следствием изменения тока 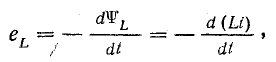
или
Э. д. с. самоиндукции пропорциональна скорости изменения тока di/dt. Она противодействует изменению тока, т. е. при увеличении тока препятствует его росту, а при уменьшении задерживает его падение (правило Ленца).
Чем быстрее изменяется ток, тем больше противодействие его росту или падению. Однако это противодействие зависит не только от скорости изменения тока, но и от конструкции электромагнитного устройства, что в формуле (10.10) выражается множителем L, т. е. индуктивностью этого устройства.
Если изменение тока в катушке является следствием изменения приложенного к ней напряжения, то э. д. с. самоиндукции направлена против приложенного напряжения, когда ток растет, и совпадает по направлению с напряжением, когда ток уменьшается.
Подобно массе, характеризующей инертность в механической системе, индуктивность характеризует инертность в электромагнитной системе.
Э.д.с. взаимоиндукции
Для системы магнитно-связанных катушек (см. рис. 8.21) э. д. с. взаимоиндукции 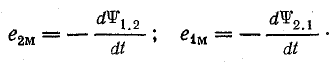
Изменение взаимного потокосцепления может быть следствием изменения тока в одной из катушек или изменения коэффициента связи.
Предположим, что изменяется ток i1 в первой катушке. Э. д. с. взаимоиндукции е2м во второй катушке пропорциональна скорости изменения этого тока: 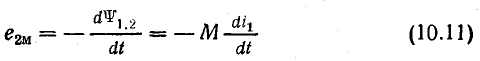
Аналогично, при изменении тока i2 э. д. с. взаимоиндукции 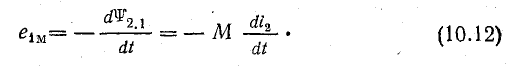
В том и другом случае коэффициентом пропорциональности является взаимоиндуктивность системы М.
Правило Ленца в применении к такой системе указывает на то, что изменение тока в одной катушке встречает противодействие со стороны другой катушки.
Из выражения (10.11) видно, что э. д. с. взаимоиндукции е2м, а следовательно, и индуктированный ток i2 имеют знак, противоположный скорости изменения тока i1. Это значит, что при увеличении тока i1 и его магнитного потока Ф1.2 индуктированный ток i2 создает магнитный поток Ф2.1, направленный встречно потоку Ф1.2; при уменьшении i1 поток Ф2.1 направлен согласно с уменьшающимся потоком Ф1.2.
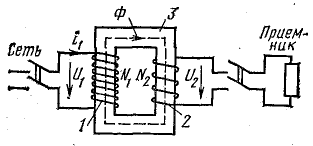
Рис. 10.11. Схема трансформатора
Аналогичное рассуждение можно привести из выражения (10.12). Направление магнитных потоков в обоих случаях, как обычно, определяется по правилу буравчика.
Взаимоиндуктивность, так же как и индуктивность, характеризует электромагнитную инерцию, но в системе катушек (контуров), имеющих магнитную связь.
Принцип действия трансформатора
Наглядным примером практического использования явления взаимоиндукции является работа трансформатора. Трансформатор — статический электромагнитный аппарат для изменения величины напряжения или тока.
Принципиальная схема трансформатора (рис. 10.11) имеет магнитопровод 3 из электротехнической стали и две обмотки на магнитопроводе: первичную 1 с числом витков N1 и вторичную 2 с числом витков N2. Обмотки выполняют из медного провода.
Первичной обмоткой трансформатор включается в сеть переменного напряжения U1 и в ней возникает ток i1. К вторичной обмотке подключается приемник электрической энергии.
Рассмотрим трансформатор с разомкнутой цепью вторичной обмотки, т. е. в режиме холостого хода.
При переменном токе в первичной обмотке создается переменный магнитный поток Ф, который замыкается по стальному сердечнику и образует потокосцепление с обеими обмотками. Таким образом, в трансформаторе обмотки электрически между собой не связаны, а связаны переменным магнитным потоком.
В обеих обмотках наводится э. д. с.: 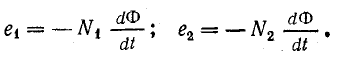
Отношение э. д. с. 
Отношение чисел витков обмоток трансформатора называется коэффициентом трансформации.
Отношение э. д. с. при холостом ходе можно заменить отношением напряжений на зажимах обмоток, учитывая, что u2 = е2 и u1 ≈ е1 (u1 > е1 на величину падения напряжения в обмотке, которое при холостом ходе мало).
Следовательно, 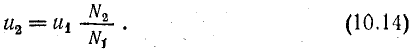
Отсюда видно, что при N2 > N1 (u2 > u1) трансформатор повышает, а при N2
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:3 14 Уравнения МаксвеллаСкачать

Электромагнитная индукция. Уравнения Максвелла для электромагнитного поля
Уравнения Максвелла для электромагнитного поля
1. Явление электромагнитной индукции
2. ЭДС индукции в движущемся проводнике
3. ЭДС индукции в неподвижном проводнике
4. Самоиндукция. Индуктивность
5. Взаимная индукция
6. Энергия магнитного поля в неферромагнитной изотропной среде
7. Работа по перемагничиванию ферромагнетика
8. Теория Максвелла
8.1. Первое уравнение Максвелла
8.2. Ток смещения. Второе уравнение Максвелла
8.3. Теорема Остроградского-Гаусса. Третье и четвёртое уравнения Максвелла
8.4. Полная система уравнений Максвелла
8.5. Частные случаи: стационарное поле; поле в свободном пространстве
1. Явление электромагнитной индукции
При перемещении проводника в магнитном поле под действием силы Ампера (рис.16.1) совершается работа (см. предыдущую лекцию)
 |

Эта работа совершается за счёт энергии источника. Полная работа источника равна
и по закону сохранения энергии расходуется и на перемещение проводника (16.1), и на нагрев проводников. Выделяющаяся теплота по закону Джоуля-Ленца равна

где R – полное сопротивление цепи; тогда



Последнее выражение представляет собой закон Ома для полной цепи, причём в числителе, кроме ЭДС источника, появилось ещё одно слагаемое, которое естественно интерпретируется тоже как ЭДС. Это – ЭДС индукции:

Получен закон Фарадея: ЭДС индукции в замкнутом контуре равна по величине и противоположна по знаку скорости изменения магнитного потока через поверхность, натянутую на этот контур.
Знак «минус» в (16.2) является следствием закона сохранения энергии: если бы минуса не было, появившийся из-за ЭДС индукции дополнительный ток (индукционный ток 
Закон Фарадея (16.2) здесь получен для одного частного случая (деформации контура), но он универсален: ЭДС индукции можно вычислять по (16.2) независимо от того, каким способом изменяется магнитный поток 
1) можно деформировать контур (изменяем площадь);
2) перемещать контур (изменяем ориентацию контура в пространстве – угол 
3) изменять индукцию поля 
2. ЭДС индукции в движущемся проводнике можно объяснить возникновением силы Лоренца.
Пусть проводник длиной 



Электроны проводника движутся вместе с проводником, и на них действует сила Лоренца

что эквивалентно действию поля сторонних сил с напряжённостью

Под действием силы Лоренца электроны проводника перемещаются вдоль проводника (вверх на рис.15.2). Между точками (1) и (2) на концах проводника возникает разность потенциалов.
ЭДС (в данном случае – ЭДС индукции) по определению равна


То же самое можно получить по закону Фарадея (16.2). Площадь, заметённая проводником в процессе движения, равна

пересечённый магнитный поток

ЭДС индукции по (16.2)

3. ЭДС индукции в неподвижном проводнике
ЭДС индукции, возникающую в неподвижном проводнике при изменении индукции магнитного поля, объяснить силой Лоренца нельзя. Максвелл предположил, что всякое переменное магнитное поле порождает в пространстве электрическое поле 

Если 


По закону Фарадея:

где 
По определению магнитного потока


Операции дифференцирования по времени и интегрирования по пространству независимы друг от друга, поэтому их можно поменять местами; при этом производная будет частной (по времени):

Как видно, циркуляция вектора 

Циркуляция напряжённости вихревого электрического поля 


4. Самоиндукция. Индуктивность
Контур с током I создаёт в окружающем пространстве магнитное поле, индукция которого пропорциональна силе тока: 
 |
Магнитный поток через поверхность, натянутую на контур, пропорционален индукции (по определению потока 

Введём коэффициент пропорциональности между током в контуре и магнитным потоком – индуктивность контура L:


Индуктивность контура численно равна магнитному потоку, пронизывающему контур, если сила тока в контуре равна 1 А.
Для катушки с N витками нужно учитывать суммарный магнитный поток сквозь все витки, то есть полное потокосцепление


Индуктивность контура зависит от формы контура, его размеров и магнитных свойств среды. Размерность

Пример: индуктивность длинного соленоида.
Индукция поля длинного соленоида

где n – плотность намотки (число витков на единицу длины):

Магнитный поток через сечение соленоида




или, с учётом (16.7):

Поскольку 

Самоиндукция. Если в контуре изменяется сила тока, то пропорционально будет меняться и магнитный поток, что приведёт в возникновению ЭДС индукции в контуре (закон Фарадея). Это – явление самоиндукции. Самоиндукция – возникновение ЭДС индукции в контуре при изменении силы тока в нём.

Будем считать коэффициент самоиндукции L постоянным, тогда

При замыкании или размыкании цепи токи резко меняются. Если индуктивность контура велика, то из-за возникновения ЭДС самоиндукции индукционный ток может быть много больше тока, на который рассчитана нагрузка:

Такие токи называются экстратоками замыкания или размыкания. Именно возникновение таких токов объясняет, почему лампочки чаще перегорают в момент включения или выключения.
5. Взаимная индукция
 |
Рассмотрим два контура L1 и L2 с токами I1 и I2 соответственно, расположенные не слишком далеко друг от друга так, чтобы линии индукции B1 поля, созданного током I1 первого контура, пронизывали второй контур (рис.16.5).
Магнитный поток 

Введём коэффициент пропорциональности – коэффициент взаимной индукции двух контуров:


И наоборот, если ток I2 во втором контуре создаёт поле с индукцией B2, то магнитный поток 

Можно показать, что коэффициент пропорциональности в (16.10) и (16.11) один и тот же:

Коэффициент взаимной индукции зависит от формы, размеров обоих контуров, из взаимного расположения и магнитных свойств окружающей среды. Как и коэффициент самоиндукции, он измеряется в генри:

 |
Пример: рассмотрим две катушки на общем ферромагнитном сердечнике (рис.16.6).
Число витков первой катушки равно N1, второй – N2; длина сердечника (тороида) по средней линии равна l, площадь сечения тороида – S. Линии индукции B1 магнитного поля, созданного током первой катушки, пронизывают все витки второй катушки, причём

магнитный поток через сечение сердечника

полное потокосцепление (суммарный поток через все N2 витков второй катушки) для второй катушки

а коэффициент взаимной индукции катушек

Заметим, что 
Если изменяется сила тока I1 в первом контуре, то по закону Фарадея и по (16.10) ЭДС индукции во втором контуре равна:

Симметрично, при изменении тока во втором контуре ЭДС индукции в первом будет равна:

Явление взаимной индукции – это возникновение ЭДС индукции в одном контуре при изменении тока в другом контуре.
6. Энергия магнитного поля в неферромагнитной изотропной среде


По второму правилу Кирхгофа для замкнутого контура:

ЭДС здесь две: ЭДС источника 


Работа источника тока:

Отсюда энергия магнитного поля катушки

По определению (16.5) 


Если у катушки больше одного витка, нужно заменить поток 



Эта энергия локализована в пространстве, где создано магнитное поле. Рассчитаем объёмную плотность энергии, считая поле однородным. По определению, объёмная плотность энергии – это энергия единицы объёма:

Тогда из (16.15) и (16.8б):

Здесь в первых скобках – индукция поля соленоида; во вторых – напряжённость:



Поскольку 


7. Работа по перемагничиванию ферромагнетика

Работу по перемагничиванию ферромагнетика можно получить как произведение силы тока на изменение магнитного потока (точнее, полного потокосцепления в катушке):



Из (16.20) заменим 

Работа в расчёте на единицу объёма:

Она равна площади заштрихованной на графике (16.8) полоски. Работа по перемагничиванию единицы объёма ферромагнетика за один цикл равна площади петли гистерезиса, то есть интегралу:

Чем уже петля гистерезиса (меньше коэрцитивная сила HC), тем меньше потери на перемагничивание; поэтому для изготовления сердечников электромагнитов применяют магнитомягкие ферромагнетики.
8. Теория Максвелла
Теория Максвелла для электромагнитного поля – это обобщение теоремы Остроградского-Гаусса, закона полного тока и закона электромагнитной индукции Фарадея. Теория решает задачу электродинамики: найти характеристики электрического и магнитного полей системы зарядов и токов.
8.1. Первое уравнение Максвелла
По теореме о циркуляции вектора напряжённости 

По (16.4) циркуляция вектора напряжённости 



где 

Это – первое уравнение Максвелла в интегральной форме. Его смысл: электрические поля создаются как электрическими зарядами, так и изменяющимся магнитным полем.
Дифференциальную форму первого уравнения Максвелла можно получить, если воспользоваться математической теоремой Стокса: для любого векторного поля (в том числе поля 

где 

Таким образом, например, проекция ротора на ось OX равна:

Операция ротор – из той же серии, что и градиент:

Градиент конструирует из скалярного поля векторное, а ротор – из векторного снова векторное.
Градиент характеризует быстроту изменения величины (например, потенциала 
Из сравнения (16.26) и (I):

Это – первое уравнение Максвелла в дифференциальной форме.
8.2. Ток смещения. Второе уравнение Максвелла
Изменяющееся во времени магнитное поле порождает возникновение вихревого электрического поля 




Здесь 


Здесь производная – частная, поскольку D зависит в общем случае ещё и от координат, а производная – по времени. Тогда плотность тока смещения равна:

Особенности тока смещения:
1) Течёт в вакууме, где нет реальных заряженных частиц – переносчиков тока.
2) При протекании тока смещения не выделяется теплота Джоуля-Ленца.
3) Единственное положительное свойство (и назначение!) тока смещения – создавать магнитное поле.
Название «ток смещения» – из определения (16.28) через вектор электрического смещения 
Получим некоторые полезные соотношения для плотности тока смещения. Из лекции 12:

где 

Первое слагаемое 

Итак, в общем случае магнитные поля создаются токами проводимости и токами смещения. В законе полного тока (см. предыдущую лекцию)
заменим плотность тока проводимости на суммарную плотность тока проводимости и смещения:



где S – поверхность, натянутая на контур L (рис.16.11).
Уравнение (II) – второе уравнение Максвелла для электромагнитного поля в интегральной форме.
Воспользовавшись теоремой Стокса (16.26) для напряжённости магнитного поля:

получим второе уравнение Максвелла в дифференциальной форме:

Его смысл: магнитные поля создаются как токами проводимости (плотность тока проводимости – 

8.3. Теорема Остроградского-Гаусса. Третье и четвёртое уравнения Максвелла
Максвелл обобщил теорему Остроградского-Гаусса (см. лекцию 12) для любых полей, в том числе и нестационарных:

где 
Смысл теоремы: поток вектора электрического смещения 
По математической теореме Гаусса:

где 

Дивергенция завершает коллекцию операций дифференцирования по координатам векторных и скалярных полей: градиент из скаляра конструирует вектор ( 


В лекции 14 сформулирована теорема Остроградского-Гаусса для магнитного поля:

Это – четвёртое уравнение Максвелла для электромагнитного поля в интегральной форме.
Аналогично в дифференциальной форме:

Смысл этого уравнения: магнитных зарядов нет.
8.4. Полная система уравнений Максвелла
Полная система уравнений Максвелла включает, кроме приведённых четырёх основных, ещё три так называемых материальных. Эти три связывают характеристики полей со свойствами среды и друг с другом и включают, в частности, закон Ома в дифференциальной форме. Вот полная система в интегральной и в дифференциальной формах:

8.5. Частные случаи: стационарное поле; поле в свободном пространстве
Если поля стационарные, все производные равны нулю:

Поля – магнитное и электрическое – разделяются. Их характеристики не связаны друг с другом.
Второй частный случай – поля в свободном пространстве, где нет ни зарядов, ни токов проводимости:

Рассмотрим систему двух первых уравнений Максвелла для свободного пространства:

Изменение магнитного поля 



🎬 Видео
ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Раскрытие тайн электромагнитной волныСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Вывод уравнений МаксвеллаСкачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

Уравнения Максвелла и электромагнитные волныСкачать

Урок 282. Закон Фарадея для электромагнитной индукцииСкачать

Уравнения Максвелла 2021Скачать

39 Уравнения МаксвеллаСкачать

3 Уравнения Максвелла в дифференциальной формеСкачать

Уравнения Максвелла — Мартин МакколлСкачать

Уравнения Максвелла в вакууме. Потенциалы электромагнитного поля.Скачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
Уравнения Максвелла. Вихревое электрическое поле. Ток смещенияСкачать

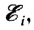 возникающая в замкнутом контуре, прямо пропорциональна скорости изменения магнитного потока через него:
возникающая в замкнутом контуре, прямо пропорциональна скорости изменения магнитного потока через него: