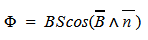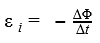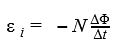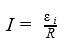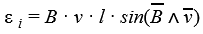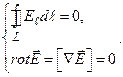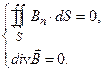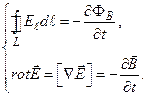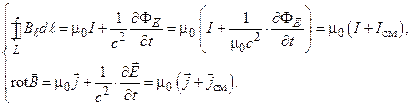Уравнение магнитной индукции от времени

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Магнитный поток

Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.

Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

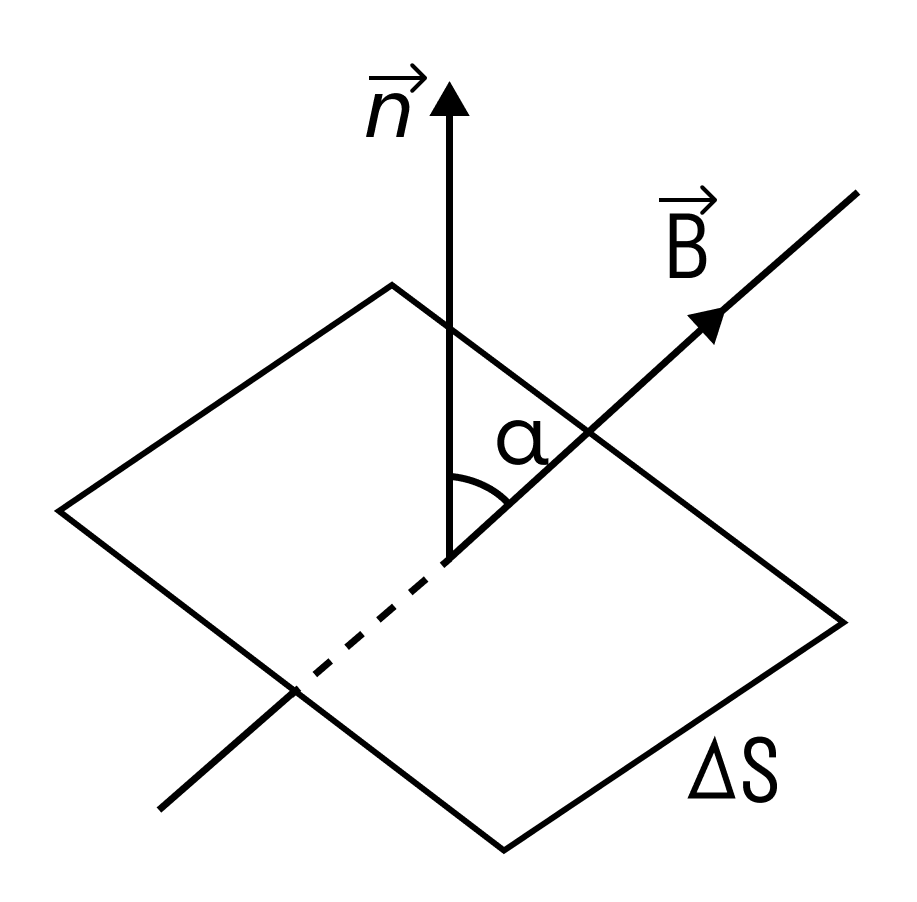
Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​B​, площади поверхности ​S​, пронизываемой данным потоком, и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Магнитный поток

Ф — магнитный поток [Вб]

B — магнитная индукция [Тл]

S — площадь пронизываемой поверхности [м^2]

n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Видео:ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.

Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки

Вот, что показали эти опыты:

1. Индукционный ток возникает только при изменении линий магнитной индукции.
2. Направление тока будет различно при увеличении числа линий и при их уменьшении.
3. Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Закон Фарадея

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

N — количество витков [-]

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:

Закон Ома для проводящего контура

Ɛi — ЭДС индукции [В]

I — сила индукционного тока [А]

R — сопротивление контура [Ом]

Если проводник длиной l будет двигаться со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B​ ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника

Ɛi — ЭДС индукции [В]

B — магнитная индукция [Тл]

v — скорость проводника [м/с]

l — длина проводника [м]

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
• вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Видео:Физика 9 класс (Урок№19 - Индукция магнитного поля.)Скачать

Правило Ленца

Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.

Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.

Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Электромагнитная индукция

Видео:Магнитное поле. Магнитная индукция | Физика 11 класс #1 | ИнфоурокСкачать

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Видео:Как магнитное поле назвали магнитной индукциейСкачать

Магнитный поток

Магнитным потоком через площадь ​ ( S ) ​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​ ( B ) ​, площади поверхности ​ ( S ) ​, пронизываемой данным потоком, и косинуса угла ​ ( alpha ) ​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​ ( Phi ) ​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​ ( alpha ) ​ магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Видео:Электромагнитная индукция. Простыми словамиСкачать

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​ ( N ) ​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​ ( R ) ​:

При движении проводника длиной ​ ( l ) ​ со скоростью ​ ( v ) ​ в постоянном однородном магнитном поле с индукцией ​ ( vec ) ​ ЭДС электромагнитной индукции равна:

где ​ ( alpha ) ​ – угол между векторами ​ ( vec ) ​ и ( vec ) .

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Видео:Линии магнитной индукции наглядно. Правило правой рукиСкачать

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Видео:Электромагнитная индукция. Магнитный поток. Правило Ленца | Физика 11 класс #4 | ИнфоурокСкачать

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​ ( varepsilon_ ) ​, возникающая в катушке с индуктивностью ​ ( L ) ​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Видео:Электромагнитная индукция. ЕГЭ Физика. Николай НьютонСкачать

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​ ( Phi ) ​ через контур из этого проводника пропорционален модулю индукции ​ ( vec ) ​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​ ( L ) ​ между силой тока ​ ( I ) ​ в контуре и магнитным потоком ​ ( Phi ) ​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Видео:Поток вектора магнитной индукцииСкачать

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Видео:Галилео. Эксперимент. Электромагнитная индукцияСкачать

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

Видео:Электромагнитная индукция за 1 минутуСкачать

Зависимость эдс от времени формула

Четыре металлические рамки находятся в однородном магнитном поле. Направление вектора магнитной индукции и начальное расположение рамок показано на рис. 1: плоскости рамок 1 и 4 перпендикулярны оси 0z, плоскость рамки 2 перпендикулярна оси 0y и плоскость рамки 3 перпендикулярна оси 0x.

В некоторый момент времени (см. рис. 2)

рамку № 1 начинают вращать вокруг оси 0y;

рамку № 2 начинают вращать вокруг оси 0x;

рамку № 3 начинают перемещать с постоянной скоростью параллельно оси 0x;

рамку № 4 начинают перемещать с постоянным ускорением параллельно оси 0z. Для какой из этих рамок на рис. 3 правильно изображена зависимость ЭДС индукции, возникающей в рамке, от времени t?

Явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией. Так как поле постоянно, то перемещения рамок 3 и 4 не приводят к изменению магнитного потока.

Величина ЭДС индукции в контуре определяется выражением:

Как видно из рисунка, площадь рамки 2 в начальный момент времени увеличивается, а это означает, что значение ЭДС будет отрицательно.

Про­во­лоч­ная рамка со­про­тив­ле­ни­ем R и пло­ща­дью S на­хо­дит­ся в од­но­род­ном по­сто­ян­ном маг­нит­ном поле линии ин­дук­ции ко­то­ро­го пер­пен­ди­ку­ляр­ны плос­ко­сти рамки. В мо­мент вре­ме­ни t = 0 рамка на­чи­на­ет вра­щать­ся с ча­сто­той n обо­ро­тов в се­кун­ду во­круг оси, ле­жа­щей в плос­ко­сти рамки. Уста­но­ви­те для мо­мен­та вре­ме­ни t > 0 со­от­вет­ствие между фи­зи­че­ски­ми ве­ли­чи­на­ми и вы­ра­жа­ю­щи­ми их фор­му­ла­ми. К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию из вто­ро­го столб­ца и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

А) поток век­то­ра маг­нит­ной ин­дук­ции через плос­кость рамки

Б) мо­дуль ЭДС ин­дук­ции, воз­ни­ка­ю­щей в рамке

1)

2)

3)

4)

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам:

Маг­нит­ный поток через рамку равен про­из­ве­де­нию пло­ща­ди рамки на ве­ли­чи­ну век­то­ра маг­нит­ной ин­дук­ции и на ко­си­нус угла между пер­пен­ди­ку­ля­ром к рамке и на­прав­ле­ни­ем поля. За­ви­си­мость маг­нит­но­го по­то­ка от вре­ме­ни имеет вид

При вра­ще­нии рамки в маг­нит­ном поле в ней воз­ни­ка­ет ЭДС ин­дук­ции, рав­ная, по за­ко­ну элек­тро­маг­нит­ной ин­дук­ции Фа­ра­дея,

Про­во­лоч­ную рамку рав­но­мер­но вра­ща­ют в од­но­род­ном маг­нит­ном поле так, что за­ви­си­мость маг­нит­но­го по­то­ка через рамку от вре­ме­ни имеет вид: Мак­си­маль­ное зна­че­ние мо­ду­ля ЭДС ин­дук­ции, воз­ни­ка­ю­щей в рамке, равно

1)

2)

3)

4)

ЭДС ин­дук­ции рас­счи­ты­ва­ет­ся по фор­му­ле Мак­си­маль­ное зна­че­ние ко­си­ну­са равно еди­ни­це, сле­до­ва­тель­но, мак­си­маль­ное зна­че­ние мо­ду­ля ЭДС ин­дук­ции, воз­ни­ка­ю­щей в рамке равно

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Про­во­лоч­ную рамку рав­но­мер­но вра­ща­ют в од­но­род­ном маг­нит­ном поле так, что за­ви­си­мость маг­нит­но­го по­то­ка через рамку от вре­ме­ни имеет вид: Мак­си­маль­ное зна­че­ние мо­ду­ля ЭДС ин­дук­ции, воз­ни­ка­ю­щей в рамке, равно

1)

2)

3)

4)

ЭДС ин­дук­ции рас­счи­ты­ва­ет­ся по фор­му­ле Мак­си­маль­ное зна­че­ние ко­си­ну­са равно еди­ни­це, сле­до­ва­тель­но, мак­си­маль­ное зна­че­ние мо­ду­ля ЭДС ин­дук­ции, воз­ни­ка­ю­щей в рамке равно

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

При электромагнитных колебаниях в колебательном контуре, состоящем из конденсатора и катушки индуктивности, последовательно реализуются следующие состояния.

1) Конденсатор полностью заряжен, а ток через катушку не протекает.

2) Конденсатор разряжается, а сила тока, текущего через катушку, увеличивается.

3) Конденсатор полностью разряжен, а сила тока, текущего через катушку, максимальна.

4) Сила тока, текущего через катушку, уменьшается, а конденсатор заряжается.

В каком из этих состояний ЭДС индукции, действующая в катушке, равна нулю?

ЭДС индукции вычисляется по формуле следовательно, ЭДС индукции равно нулю в том случае, когда производная от тока по времени равна нулю. Пусть заряд пропорционален косинусу: тогда а Заметим, что состояние, когда конденсатор полностью разряжен, а сила тока, текущего через катушку, максимальна соответствует состоянию с Эти закономерности проще увидеть, если выполнить графики этих функций (см. рис.). Также заметим, что система переходит из состояния 1 в состояние 4 за половину периода.

Таким образом, правильный ответ указан под номером 3.

А почему первый ответ не подходит? Ведь в этом случае тоже экстремум функции изменения тока?

Здравствуйте! В первом случае экстремума у тока не будет. Добавили более полное пояснение, теперь ясно видно, в каких точках все величины имеют экстремумы и нули.

При электромагнитных колебаниях в колебательном контуре, состоящем из конденсатора и катушки индуктивности, последовательно реализуются следующие состояния.

1. Конденсатор полностью разряжен, а сила тока, текущего через катушку, максимальна.

2. Сила тока, текущего через катушку, уменьшается, а конденсатор заряжается.

3. Конденсатор полностью заряжен, а ток через катушку не протекает.

4. Конденсатор разряжается, а сила тока, текущего через катушку, увеличивается.

В каком из этих состояний ЭДС индукции, действующая в катушке, максимальна по модулю?

ЭДС индукции вычисляется по формуле следовательно, ЭДС индукции равно нулю в том случае, когда производная от тока по времени равна нулю. Пусть заряд пропорционален синусу: тогда а Заметим, что состояние, когда конденсатор полностью заряжен, а ток через катушку не протекает соответсвует состоянию с наибольшим Следовательно, правильный ответ указан под номером 3. Эти закономерности проще увидеть, если выполнить графики этих функций (см. рис.). Также заметим, что система переходит из состояния 1 в состояние 4 за половину периода.

Таким образом, правильный ответ указан под номером 3.

На же­лез­ный сер­деч­ник на­де­ты две ка­туш­ки, как по­ка­за­но на ри­сун­ке. По пра­вой ка­туш­ке про­пус­ка­ют ток, ко­то­рый ме­ня­ет­ся со­глас­но при­ведённому гра­фи­ку. На ос­но­ва­нии этого гра­фи­ка вы­бе­ри­те два вер­ных утвер­жде­ния. Ин­дук­тив­но­стью ка­ту­шек пре­не­бречь.

1) В про­ме­жут­ке между 1 с и 2 с ЭДС ин­дук­ции в левой ка­туш­ке равна 0.

2) В про­ме­жут­ках 0−1 с и 3−5 с на­прав­ле­ния тока в левой ка­туш­ке были оди­на­ко­вы.

3) В про­ме­жут­ке между 1 с и 2 с ин­дук­ция маг­нит­но­го поля в сер­деч­ни­ке была равна 0.

4) Сила тока через ам­пер­метр была от­лич­на от 0 толь­ко в про­ме­жут­ках 0−1 с и 3−5 с.

5) Сила тока в левой ка­туш­ке в про­ме­жут­ке 0−1 с была боль­ше, чем в про­ме­жут­ке 2−3 с.

Обратим внимание, что авторы задачи просят пренебречь индуктивностью катушек, это означает, что магнитный поток в катушках изменяется одновременно, не испытывая задержек. Таким образом, ток в левой катушке будет пропорционален производной от тока в правой катушке.

1) В промежутке между 1 с и 2 с ток в правой катушке остаётся неизменным, следовательно, магнитный поток через левую катушку остаётся неизменным, значит, ЭДС индукции в левой катушке равна нулю.

2) В промежутке 0−1 с и в промежутке 3−5 с ток в правой катушке уменьшается, следовательно, направления токов, индуцированных в левой катушке одинаковы.

3) В промежутке между 1 с и 2 с ток в правой катушке отличен от нуля, следовательно, индукция магнитного поля в сердечнике также отлична от нуля.

4) Заметим, что в промежуток времени 2−3 с ток в правой катушке изменяется, следовательно, сила тока, индуцированного в левой катушке отлична от нуля и в этот промежуток времени.

5) В промежутке 0−1 с и в промежутке 2−3 с производная тока по времени одинакова по модулю, следовательно, силы токов, индуцированных в левой катушке одинаковы.

Таким образом, верны утверждения 1 и 2.

На ри­сун­ке по­ка­зан гра­фик за­ви­си­мо­сти маг­нит­но­го по­то­ка, про­ни­зы­ва­ю­ще­го кон­тур, от вре­ме­ни. На каком из участ­ков гра­фи­ка (1, 2, 3 или 4) в кон­ту­ре воз­ни­ка­ет мак­си­маль­ная по мо­ду­лю ЭДС ин­дук­ции?

ЭДС по мо­ду­лю равна ско­ро­сти из­ме­не­ния маг­нит­но­го по­то­ка. Чем боль­ше ско­рость из­ме­не­ния маг­нит­но­го по­то­ка, тем боль­ше ЭДС ин­дук­ции. Мо­дуль ско­ро­сти из­ме­не­ния маг­нит­но­го по­то­ка мак­си­ма­лен на участ­ке 2.

Го­ри­зон­таль­ный про­вод­ник дли­ной 1 м дви­жет­ся рав­но­уско­рен­но в вер­ти­каль­ном од­но­род­ном маг­нит­ном поле, ин­дук­ция ко­то­ро­го равна 0,5 Тл. Ско­рость про­вод­ни­ка го­ри­зон­таль­на и пер­пен­ди­ку­ляр­на про­вод­ни­ку (см. ри­су­нок). При на­чаль­ной ско­ро­сти про­вод­ни­ка, рав­ной нулю, про­вод­ник пе­ре­ме­стил­ся на 1 м. ЭДС ин­дук­ции на кон­цах про­вод­ни­ка в конце пе­ре­ме­ще­ния равна 2 В. Ка­ко­во уско­ре­ние про­вод­ни­ка?

ЭДС ин­дук­ции в про­вод­ни­ке, дви­жу­щем­ся в од­но­род­ном маг­нит­ном поле:

Из­ме­не­ние маг­нит­но­го по­то­ка за малое время : где пло­щадь опре­де­ля­ет­ся про­из­ве­де­ни­ем длины про­вод­ни­ка на его пе­ре­ме­ще­ние за время т. е.

Сле­до­ва­тель­но, где — ско­рость дви­же­ния про­вод­ни­ка.

В конце пути дли­ной ско­рость про­вод­ни­ка ( — уско­ре­ние), так что от­сю­да

Ответ:

Как вы нашли скорость проводника в конце пути? Объясните, пожалуйста, поподробнее. И разве нельзя было в выражении B*l*x/t выразить t как sqrt(2*x/a)? Тогда и ответ получается другой.

Так, как Вы предлагаете, действовать нельзя, и другой ответ тому подтверждение 🙂

Проводник движется равноускоренно, его скорость увеличивается со временем, это приводит к тому, что величина ЭДС между концами проводника не постоянна. Обратите внимание, существенно, что при выводе формулы рассматривается перемещение проводника за малый интервал времени . Так вы находите мгновенное значение ЭДС, ежели попытаться применить эту формулу ко всему времени разгона, Вы получите среднее значение ЭДС,а оно, конечно, отличается от искомой величины.

По поводу второго Вашего вопроса. Здесь используется так называемая формула «без времени»: . Начальная скорость проводника равна нулю . Следовательно к тому времени, когда проводник пройдет 1 м, он приобретет скорость: .

Почему здесь не возникает сила Ампера или сила Лоренца ( действующая на свободные заряды в проводнике) ?

Возникает, конечно, именно она и приводит к появлению ЭДС на концах проводника.

В решении вашей задачи вы приравниваете ЭДС индукции с начала к выражению (BLX)/t (Извините не знаю как писать дельта по этому её я пропускаю ), затем вы приравниваете полученное выражение к BLV, но формула ЭДС=BLV справедлива только при равномерном движении проводника. На мой взгляд для данной задачи будут характерны следующие преобразования формулы ЭДС: ЭДС= Ф/t ; Ф=BS (S- площадь определяемая произведением длинны проводника L на его перемещение X ) перемещение X= (at^2)/2(c учётом что начальная скорость=0) , где а-ускорение и определяется как разность скоростей в промежуток времени(его я взял равным промежутку времени движения в задаче), но так как начальная скорость =0, то а=v/t , где v-конечная скорость тела, подставив получившееся выражение для определения ускорения в выражение для определения перемещения мы получим следующее: X=((V/t)t^2)/2 = Vt/2. Таким образом S=LVt/2 и ЭДС=B(LVt/2)/t=BLV/2. В остальном ваша задача решена правильно, но из-за того что 2 в знаменателе упущена ответ не тот который должен быть. Если посчитаете, что я прав, то исправьте пожалуйста ошибку.

Формула . Она выводится для малого перемещения, в результате получается мгновенная скорость. Дальше мы смотрим только на конечный момент времени, так как про значение напряжения в промежуточные моменты времени нам ничего не известно.

1.Мгновенное значение ЭДС индукции определяется формулой закона Фарадея (18.4):

.

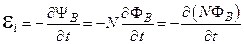
При вращении рамки магнитный поток изменяется по закону :

, где — угловая частота.

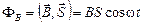
Тогда мгновенное значение ЭДС индукции мы найдем по формуле(18.1), аналогичной (18.1), но с учетом числа витков N:

,(18.40)

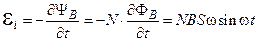
подставив значение .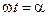

Произведя вычисления по формуле (18.40), получим:

=47,1 В.

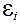
2.Максимальное значение ЭДС индукции равно амплитудному значению — согласно формуле

(18.41)

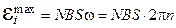
Произведя вычисления по формуле (18.41), получим:

= 94,2 В.

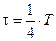
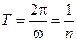
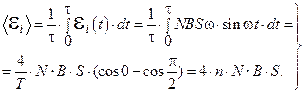
3.Среднее значение ЭДС за минимальное время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения, то есть за , где (поскольку поток изменяется по косинусоидальному закону):

(18.42)

Произведя вычисления по формуле (18.42), получим:

ТЕМА 19. Законы электромагнитного поля — уравнения Максвелла

В предыдущих темах были рассмотрены экспериментально установленные основные законы электрических и электромагнитных явлений:

закон полного тока Ампера и

закон электромагнитной индукции Фарадея-Ленца.

Законы электромагнитного поля сформулированы Дж.К.Максвеллом как обобщение экспериментальных фактов. Они позволяют решать основную задачу, возникающую при изучении электромагнитных явлений: по заданному распределению зарядов и токов отыскать созданные ими в каждой точке пространства электрические и магнитные поля.

Математическая запись этих законов – уравнения Максвелла — в современном виде сделана Г.Герцем и О.Хевисайдом.

Система уравнений Максвелла для статических полей ( в вакууме):

I. ,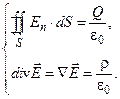

II.

III.

IV.

Уравнения I и II характеризуют электростатическое поле и указывают на существование электрических зарядов, на которых начинаются и кончаются силовые линии электрического поля. Равенство нулю циркуляции указывает на потенциальный характер электростатического поля (силовые линии поля не замкнуты – либо расходятся, либо сходятся).

Уравнения III и IVхарактеризуют магнитостатическое поле и указывают на источник магнитостатического поля – постоянные электрические токи. Равенство нулю потока вектора 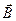указывает на отсутствие магнитных зарядов: силовые линии магнитного поля замкнуты, то есть магнитное поле – вихревое.

Система уравнений Максвелла для переменных полей ( в вакууме):

.

.

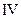
Уравнение II указывает на новый источник электрического поля – переменное магнитное поле, и возникающее электрическое поле оказывается тоже новым — вихревым.

Уравнение IV указывает на новый источник магнитного поля – переменное электрическое поле, но возникающее при этом магнитное поле оказывается таким же, как и в статике, — вихревым.

В этой публикации рассмотрены основные термины, законы и методики вычисления ЭДС магнитной индукции. С помощью представленных ниже материалов можно самостоятельно определить силу тока во взаимосвязанных контурах, изменение напряжения в типовых трансформаторах. Эти сведения пригодятся для решения различных электротехнических задач.

Видео:Физика 11 класс (Урок№5 - Электромагнитная индукция.)Скачать

Магнитный поток

Известно, что пропускание тока через проводник сопровождается формированием электромагнитного поля. На этом принципе основана работа динамиков, запорных устройств, приводов реле, других приспособлений. Изменением параметров источника питания получают необходимые силовые усилия для перемещения (удержания) совмещенных деталей, обладающих ферромагнитными свойствами.

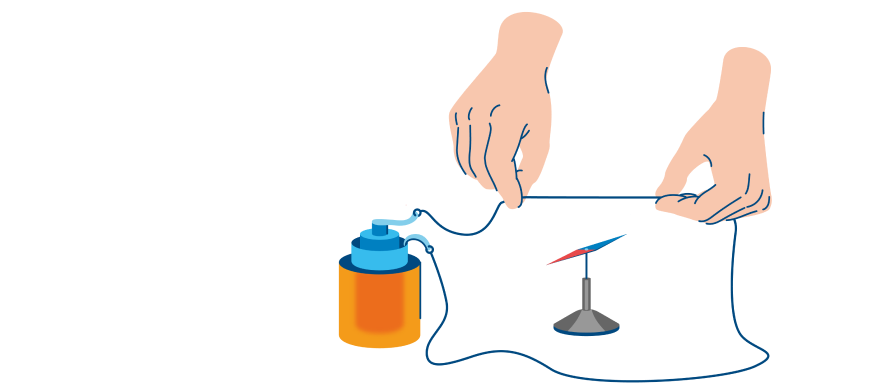
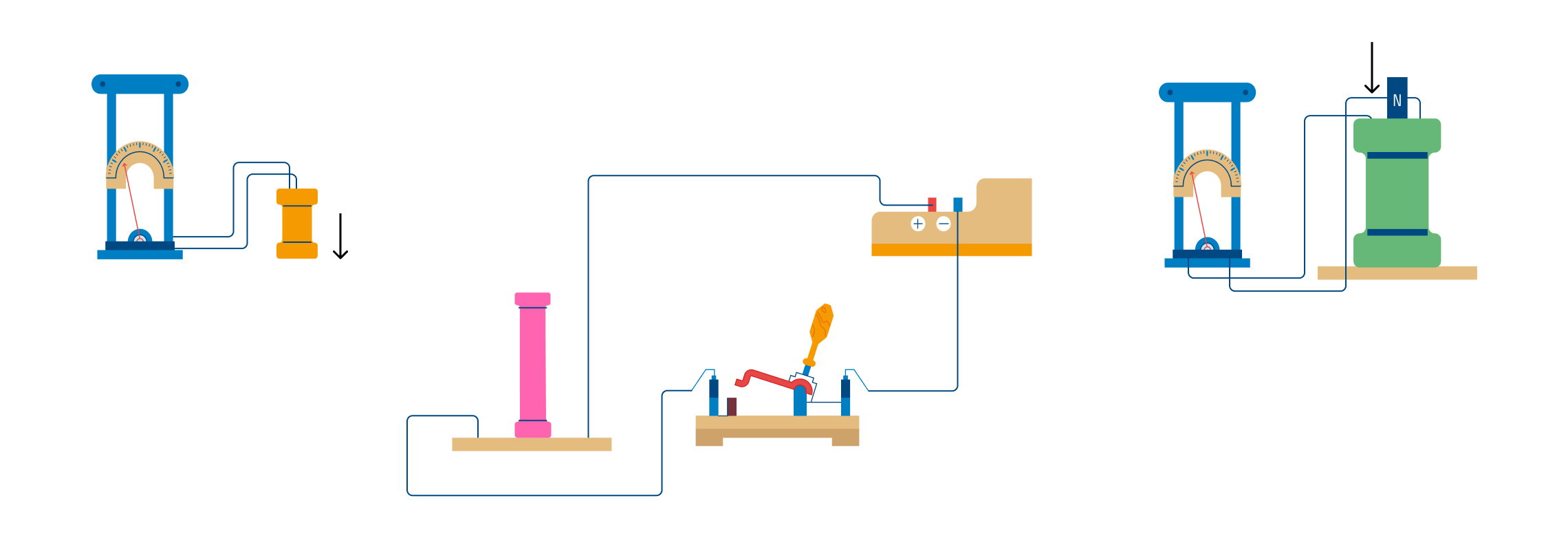
Однако действительно и обратное утверждение. Если между полюсами постоянного магнита перемещать рамку из проводящего материала по соответствующему замкнутому контуру, начнется перемещение заряженных частиц. Подключив соответствующие приборы, можно регистрировать изменение тока (напряжения). В ходе элементарного эксперимента можно выяснить увеличение эффекта в следующих ситуациях:

• перпендикулярное расположение проводника/силовых линий;
• ускорение перемещений.

На картинке выше показано, как определять направление тока в проводнике с помощью простого правила.

Видео:Крайон. История Древней Души. Магнитная Решетка Земли. Тьма живая?Скачать

Что такое ЭДС индукции

Отмеченное выше перемещение зарядов создает разницу потенциалов, если контур разомкнут. Представленная формула показывает, как именно будет зависеть ЭДС от основных параметров:

• векторного выражения магнитного потока (B);
• длины (l) и скорости перемещения (v) контрольного проводника;
• угла (α) между векторами движения/ индукции.

Аналогичный результат можно получить, если система составлена из стационарной проводящей цепи, на которую воздействует перемещающееся магнитное поле. Замкнув контур, создают подходящие условия для перемещения зарядов. Если использовать много проводников (катушку) или двигаться быстрее, увеличится сила тока. Представленные принципы с успехом применяют для преобразования механических сил в электроэнергию.

Видео:Закон электромагнитной индукцииСкачать

Обозначение и единицы измерения

ЭДС в формулах обозначают вектором Е. Подразумевается напряженность, которую создают сторонние силы. Соответствующим образом эту величину можно оценивать по разнице потенциалов. По действующим международным стандартам (СИ), единица измерения – один вольт. Большие и малые значения указывают с применением кратных приставок: «микро», «кило» и др.

Видео:Электромагнитная индукцияСкачать

Законы Фарадея и Ленца

Если рассматривается электромагнитная индукция, формулы этих ученых помогают уточнить взаимное влияние значимых параметров системы. Определение Фарадея позволяет уточнить зависимость ЭДС (E – среднее значение) от изменений магнитного потока (ΔF) и времени (Δt):

Промежуточные выводы:

• ток увеличивается, если за единицу времени проводник пересекает большее количество силовых магнитных линий;
• «-» в формуле помогает учитывать взаимные связи между полярностью Е, скоростью перемещения рамки, направленностью вектора индукции.

Ленц обосновал зависимость ЭДС от любых изменений магнитного потока. При замыкании контура катушки создаются условия для движения зарядов. В таком варианте конструкция преобразуется в типичный соленоид. Рядом с ним образуется соответствующее электромагнитное поле.

Этот ученый обосновал важную особенность индукционной ЭДС. Сформированное катушкой поле препятствует изменению стороннего потока.

Видео:Урок 282. Закон Фарадея для электромагнитной индукцииСкачать

Движение провода в магнитном поле

Как показано в первой формуле (Е = В * l * v * sinα), амплитуда электродвижущей силы в значительной мере зависит от параметров проводника. Точнее – влияние оказывает количество силовых линий на единицу длины рабочей области цепи. Аналогичный вывод можно сделать с учетом изменения скорости перемещения. Следует не забывать о взаимном расположении отмеченных векторных величин (sinα).

Важно! Перемещение проводника вдоль силовых линий не провоцирует индуцирование электродвижущей силы.

Видео:Урок 20. Магнитная индукция, магнитный поток, магнитная цепьСкачать

Вращающаяся катушка

Обеспечить оптимальное расположение функциональных компонентов при одновременном перемещении сложно, если применять представленный в примере прямой провод. Однако согнув рамку, можно получить простейший генератор электроэнергии. Максимальный эффект обеспечивает увеличение количества проводников на единицу рабочего объема. Соответствующая отмеченным параметрам конструкция – катушка, типичный элемент современного генератора переменного тока.

Для оценки магнитного потока (F) можно применить формулу:

где S – площадь рассматриваемой рабочей поверхности.

Пояснение. При равномерном вращении ротора происходит соответствующее циклическое синусоидальное изменение магнитного потока. Аналогичным образом меняется амплитуда выходного сигнала. Из рисунка понятно, что определенное значение имеет величина зазора между основными функциональными компонентами конструкции.

ЭДС самоиндукции

Если через катушку пропускать переменный ток, рядом будет формироваться электромагнитное поле с аналогичными (равномерно изменяющимися) силовыми характеристиками. Оно создает переменный синусоидальный магнитный поток, который, в свою очередь, провоцирует перемещение зарядов и образование электродвижущей силы. Данный процесс называют самоиндукцией.

С учетом рассмотренных базовых принципов несложно определить, что F = L * l. Значение L (в генри) определяет индуктивные характеристики катушки. Этот параметр зависит от количества витков на единицу длины (l) и площади поперечного сечения проводника.

Взаимоиндукция

Если собрать модуль из двух катушек, в определенных условиях можно наблюдать явление взаимной индукции. Элементарное измерение покажет, что по мере увеличения расстояния между элементами уменьшается магнитный поток. Обратное явление наблюдается по мере уменьшения зазора.

Чтобы находить подходящие компоненты при создании электрических схем, необходимо изучить тематические вычисления:

• можно взять для примера катушки с разным количеством витков (n1 и n2);
• взаимоиндукция (M2) при прохождении по первому контуру токаI1 будет вычислена следующим образом:

• после преобразования этого выражения определяют значение магнитного потока:

• для расчета эдс электромагнитной индукции формула подойдет из описания базовых принципов:

E2 = – n2 * ΔF/ Δt = M 2 * ΔI1/ Δt

При необходимости можно найти по аналогичному алгоритму соотношение для первой катушки:

E1 = – n1 * ΔF/ Δt = M 1 * ΔI2/ Δt.

Следует обратить внимание, что в этом случае значение имеет сила (I2) во втором рабочем контуре.

Совместное влияние (взаимоиндукцию – М) рассчитывают по формуле:

Специальным коэффициентом (K) учитывают действительную силу связи между катушками.

Где используются разные виды ЭДС

Перемещение проводника в магнитном поле применяют для генерации электроэнергии. Вращение ротора обеспечивают за счет разницы уровней жидкости (ГЭС), энергией ветра, приливами, топливными двигателями.

Различное количество витков (взаимоиндукцию) применяют для изменения нужным образом напряжения во вторичной обмотке трансформатора. В таких конструкциях взаимную связь увеличивают с помощью ферромагнитного сердечника. Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.

Видео