Метод функций Ляпунова состоит в непосредственном исследовании устойчивости положения равновесия системы
при помощи подходящим образом подобранной функции — функции Ляпунова , причем делается это без предварительного нахождения решений системы.
Ограничимся рассмотрением автономных систем
для которых , есть точка покоя.
Функция , определенная в некоторой окрестности начала координат, называется знакоопределенной (определенно-положительной или определенно-отрицательной), если она в области
где — достаточно малое положительное число, может принимать значения только одного определенного знака и обращается в ноль лишь при . Так, в случае функции
будут определенно-положительными, причем здесь величина 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> может быть взята сколько угодно большой.
Функция называется знакопостоянной (положительной или отрицательной), если она в области (2) может принимать значения только одного определенного знака, но может обращаться в ноль и при . Например, функция
будет знакопостоянной (положительной). В самом деле, функцию можно записать так: откуда видно, что она обращается в ноль и при , а именно при и любых и таких, что .
Пусть есть дифференцируемая функция своих аргументов и пусть являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции по времени будем иметь:
Величина , определяемая формулой (3), называется полной производной функции по времени , составленной в силу системы уравнений (1).
Теорема (1) Ляпунова об устойчивости. Если для системы дифференциальных уравнений (1) существует знакоопределенная функция (функция Ляпунова), полная производная которой по времени, составленная в силу системы (1), есть функция знакопостоянная, знака, противоположного с , или тождественно равная нулю, то точка покоя , системы (1) устойчива.
Теорема (2) Ляпунова об асимптотической устойчивости. Если для системы дифференциальных уравнений (I) существует знакоопределенная функция , полная производная которой по времени, составленная в силу системы (1), есть также функция знакоопределенная, знака противоположного с , то тонка покоя системы (1) асимптотически устойчива.
Пример 1. Исследовать на устойчивость точку покоя системы
Решение. Выберем в качестве функции функцию . Эта функция определенно-положительная. Производная функции в силу системы (4) равна
Из теоремы 1 следует, что точка покоя системы (4) устойчива. Однако асимптотической устойчивости нет: траектории системы (4) — окружности и они не стремятся к точке при .
Пример 2. Исследовать на устойчивость точку покоя системы
Решение. Беря опять , найдем
Таким образом, есть определенно-отрицательная функция. В силу теоремы 2 точка покоя системы (5) устойчива асимптотически.
Общего метода построения функции Ляпунова нет. В простейших случаях функцию Ляпунова можно искать в виде
Пример 3. С помощью функции Ляпунова исследовать на устойчивость тривиальное решение системы
Решение. Будем искать функцию Ляпунова в виде , где 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEEAAAATBAMAAAA9n32KAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAgMAQm2PQMVEh4EHwsOP1aAYAAAEZSURBVCjPY2AgAbAqBaALWU9A4bLrNaApYFyoZIAi4GeApkLGgFcBRSANYlkwXGAJA8drZAXMTyB0mDDM2ocM3A9BEkHOzWABjodOAhAlklCnP2RgfgSkzRyqnoMFWJ5NXgg1xRPiUKABIBVaDEwPwAJsixl0oOZv8kRSwfqUgQfiYDsHBj2YmzapI1QwvWSog1jf18DwBqaiBKqCHaiCZwGD3AawqNwE7icwI26DSKBHQCJAK+6xNJgCA0uOgeUlREETxKUMRxg4njIw8CawPmIzkAM6pc6gDhIxUVAFDF4GLAsYGDhTLsZcZegDeoclJQM1xBhMUr0KgBQnAzOQAnnHHBJOwohgLkTEJfMFQmmDpYGQChPcUgBSQj3qZ+tWewAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> — произвольные параметры. Имеем
Полагая , получим, что . Таким образом, при всяком 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA8FGBQWahAcAh4NARsTGRMv0AhAAAAM9JREFUKM+1kttyhiAMhDmEHAAl7/+0Tfg7VcSL9qLOOCNhE/dbCOGfHoKT/iBPcYx6/loumkIosb9snUP2Ika3pONtFjBuHZVdX9tEEOTc4d5xMCxwpGxrYvVqicXeuvrFpQN0zp96idm+9XgSYi206gOrJXSoeKHsmeSWnvpu1hwi655tv/T98gMzJI60+WmXH4qT1yFBv+03WnnTvfv45I/2K8dFzXIDBnzkaVMt7+KkIdXREjaW23nBBmOhl/rJhMRT/bkaJ8rrDSrJ61/kMgabS6WMegAAAABJRU5ErkJggg==» /> и функция будет определенно-положительной, а ее производная , составленная в силу данной системы, является определенно-отрицательной. Из теоремы 2 Ляпунова следует, что тривиальное решение данной системы устойчиво асимптотически .
Если бы в указанной выше форме функцию не удалось найти, то ее следовало бы поискать в форме
Теорема (3) Ляпунова о неустойчивости. Пусть для системы дифференциальных уравнений (1) существует дифференцируемая в окрестности начала координат функция такая, что . Если ее полная производная , составленная в силу системы (1), есть определенно-положительная функция и сколь угодно близко от начала координат имеются точки, в которых функция принимает положи тельные значения, то точка покоя , неустойчива.
Теорема (4) Четаева о не устойчивости. Пусть для системы дифференциальных уравнений (1) существует непрерывно дифференцируемая в некоторой окрестности точки покоя , функция , удовлетворяющая в некоторой замкнутой окрестности точки покоя условиям:
1) в сколь угодно малой окрестности точки покоя существует область , в которой 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAALIAAAAWCAMAAABT2TaiAAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEXRSTlMAMSFAEOdnvAGBoVHQQpEakCM6aZIAAAK0SURBVEjH1ZeLbqswDIZztZ2ryPu/7OwkdBRYuzLpoIO0KYXg/LE/O0ap//6q6ZZlbbz8KsS7XBXez3HWHG9q7+4Kr38b3sUHxIM+DLcRCZ5eTwjiTsS9k5u7L4s2bgY4yicvzKamd0Bluk8ybtIIcnAHdwoBtv9XQXDQqBVhnY8jJrfgOV0m8nz4A0IW2Xo8WA9bMohFP+cadLGmCRkBLHtb7tDYgkrodPMltDOfGzTOeyjNXi5KbD3rume3PC/HouNWdOjiqCEplwkEkCySS5/MeFCL1LpRtyssaHiCV9j4vkmf63YovqrUstpLLjt6C25EPyTz65ayIBwS49JfMlaYAaWNuMTvVAGv2qoy/DCFlPFTyWI9NV7MvZPcRaM+elnABvGeYynle09jf1qdACAr9hwHfgUusBHPkDuRrEpcJRPM9MMhj2+7rFYwZAI+SDuRXGctzAvLXj5XTH7GRkJlf5bMYNjNjobkOBQIF6DW9NOc0PJEx61kMBPFwChT36L8HF6262p2jWMyu4GDsU+NllFmCQxX8CFAfmh6yhpK+JR+a12GUT4cG+q+rcPrSaLg0Gwk2zbO8tKqluDEwcbSt0VtztJtrmvbDBM0v4YGJxQpTOuL62idFTm1qxdiQATEbo0c+mWc3aEfJdYvsfiQ0xYM48fA8VzNf/DUReVZHp2fPjMz9lR8XevqkJR8jOBrZ1Q3+b2WInx5lPAmMxeDNYrGPB3YUtdI71imMIIvD0hzGZwt49Be5snycNTJAMdwWO9jkHAtU5z/TmQIp42DDumYtnjM/0f6HQ9zxtLC0Fr1rwrySRfmdXWjLfrG9pO2oeybzwXbLL2pHhuZxlcaR+IvKtux9EiY8zLclK9+W0D9sVs9xIo2h+t7J5vXTUm4/m1x7UOK/toBpru+hv7N9QX3VRcrTkV9YgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, причем в тех граничных точках , которые являются внутренними для (рис. 43);
2) точка покоя является граничной точкой области ;
3) в области производная , составленная в силу системы (1), определенно-положительная.
Тогда точка покоя , системы (1) неустойчива.
Пример 4. Исследовать на устойчивость точку покоя системы
Решение. Возьмем функцию . Тогда
есть функция определенно-положительная. Так как сколь угодно близко к началу координат найдутся точки, в которых 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQCAMAAABeF73YAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA6TFBocDRAV8hesERQpGwdPIJPgAAAMxJREFUKM+1UtEShCAIBAUlteL/v/agusmsm+nletgKV9hdBfjLk+eQ37Mj0oLxLXtCARCcHlboobio69HlaS7TbSqyCc+Mho042KT1XAzE88VX1ur0qoY1EAIkjRdFVboNTXmnN5CSU7KOGgYL6dwQlf1VdYY4BS32rWOsrST5qtvpbHS3bVlMK/ymH9p5a5mSociQZ+nE5D2Z6slkJYPURuX9P+25k6M7LXIhD0Ga+OiGt/ACrlz6Y6rz7ewES8GjZe4v2+MlsLKI1z9OuAYuX8p8lQAAAABJRU5ErkJggg==» /> (например, 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAF0AAAAUBAMAAAAdCCxUAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQYEBwKVnIekwENGQUbRimZIAAAFBSURBVCjPY2CgEuBUKiBJvVBZJ0nqXRi2kqQ+CaiDBMBswNWELmYojE8HTwCaAG/PCQE86lPRBSousLXjVs4YwAMO1uNwkXMMzG9wq5+tpAqmRcJhIi0GzB4GDFwhAmxRqErXuK51XXDExQ3CE3U0gITAEwNmPwMGlqkN3A+B3ImCICAOZHE5mrbOSEBoL4Vo4ASpX8CQZN3ACVJ/SQkENIEspgusr/QuINlX2gbSwPiEgcFPgEG8ToGhGcU5bAwWm1eiiCzai1DPcK6ACz2kgUZgqoe6n2G3AVsCinsYGPJQ46V0G8g9zMDw2WEA1MZgsgDFvzwBcQtYFiAp94XQcQzMT4HUboY0NNfs6jPIQXBh4ckgJ8AICpgZoQoGKOq5T0uHHoDzRCLh4dCWAXI482T0qJ3MUIzIZuEI8bJ0BgYAoe1KC73uytwAAAAASUVORK5CYII=» /> вдоль прямой ), то выполнены все условия теоремы 3 и точка покоя неустойчива (седло).
Пример 5. Исследовать на устойчивость точку покоя системы
Решение. Функция удовлетворяет условиям теоремы Четаева:
1) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQCAMAAABeF73YAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA6TFBocDRAV8hesERQpGwdPIJPgAAAMxJREFUKM+1UtEShCAIBAUlteL/v/agusmsm+nletgKV9hdBfjLk+eQ37Mj0oLxLXtCARCcHlboobio69HlaS7TbSqyCc+Mho042KT1XAzE88VX1ur0qoY1EAIkjRdFVboNTXmnN5CSU7KOGgYL6dwQlf1VdYY4BS32rWOsrST5qtvpbHS3bVlMK/ymH9p5a5mSociQZ+nE5D2Z6slkJYPURuX9P+25k6M7LXIhD0Ga+OiGt/ACrlz6Y6rz7ewES8GjZe4v2+MlsLKI1z9OuAYuX8p8lQAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> при |y|» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAVBAMAAAAJGoXuAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAwUGBpjFoQiEQUdHokXjjzxAAAAD4SURBVCjPY2AgBqRCaRY0cd4ACB0GxEZQMUY0NYwKELqYVmpYLYgwp9ADh5olTlNEYXYVuiPULPRkYGuAqGG7sE7UB+6eEHGYGnaHZwzrFCBqGhn0LB4i3NwiBlXDOOsZw70JEDWtDHkBkUj+atkFUcPG8pJhN9zNPih+nwxVw8DjwPGWQRmq5giympZjMDfXJbC9gqpRDH3MkAZX0wJ3M0OeAu9LqBq52FecO2FqSoQYkNTEbICqWe2SczEAqkbRFSkMGc/uuwBVw9nA0ACLCw+UuGjNK4C7GXuccj1jOMhAQA3zUZadhNSwbhSeAFFjiiOtssDTKgC1tztgWA8/UAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />;
2) — определенно-положительная в области |y|» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAVBAMAAAAJGoXuAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAwUGBpjFoQiEQUdHokXjjzxAAAAD4SURBVCjPY2AgBqRCaRY0cd4ACB0GxEZQMUY0NYwKELqYVmpYLYgwp9ADh5olTlNEYXYVuiPULPRkYGuAqGG7sE7UB+6eEHGYGnaHZwzrFCBqGhn0LB4i3NwiBlXDOOsZw70JEDWtDHkBkUj+atkFUcPG8pJhN9zNPih+nwxVw8DjwPGWQRmq5giympZjMDfXJbC9gqpRDH3MkAZX0wJ3M0OeAu9LqBq52FecO2FqSoQYkNTEbICqWe2SczEAqkbRFSkMGc/uuwBVw9nA0ACLCw+UuGjNK4C7GXuccj1jOMhAQA3zUZadhNSwbhSeAFFjiiOtssDTKgC1tztgWA8/UAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />.
- Метод функций Ляпунова. Устойчивость по первому (линейному) приближению
- Digiratory
- Лаборатория автоматизации и цифровой обработки сигналов
- Устойчивость нелинейных систем
- Первый метод Ляпунова
- Пример 1.
- Шаг 1. Положение равновесия:
- Шаг 2. Линеаризация для малых отклонений
- Шаг 3. Линеаризованное управление в матричной форме
- Шаг 4. Характеристический полином
- Шаг 5. Корни характеристического полинома
- Заключение об устойчивости системы
- Пример 2. Нелинейный осциллятор
- Шаг 1. Положение равновесия:
- Шаг 2. Линеаризация для малых отклонений
- Шаг 3. Линеаризованное управление в матричной форме
- Шаг 4. Характеристический полином
- Шаг 5. Корни характеристического полинома
- Заключение об устойчивости системы
- Второй метод Ляпунова
- Теорема Ляпунова об устойчивости нелинейных систем
- Пример 3. Нелинейный осциллятор
- Шаг 1. Функция Ляпунова
- Шаг 2. Частные производные
- Шаг 3. Производная функции
- Заключение об устойчивости системы
- Пример 4.
- Шаг 1. Функция Ляпунова
- Шаг 2. Частные производные
- Шаг 3. Производная функции
- Заключение об устойчивости системы
- 📽️ Видео
Видео:Функция Ляпунова 1 Теорема ЛяпуноваСкачать

Метод функций Ляпунова. Устойчивость по первому (линейному) приближению
По этой ссылке вы найдёте полный курс лекций по математике:
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции v(t, 2], 22. ж„) — так называемой функции Ляпунова, причем делается это без предварительного построения решения системы; в этом неоценимое преимущество метода. Ограничимся рассмотрением автономных систем для которых , есть точка покоя. Идея метода состоит в следующем.
Предположим, что на устойчивость исследуется точка покоя системы (1). Если бы с возрастанием t точки всех траекторий приближались к началу координат или хотя бы не удалялись от него, то рассматриваемая точка покоя была бы устойчивой. Проверка выполнения этого условия не требует знания решений системы. Действительно, если р — расстояние от точки траектории , до начала координат (производная вдоль траектории); Правая часть в (2) есть известная функция от ж„, и можно .исследовать ее знак.
Если окажется, что $0, тоточкннавс^с тдаедориях^удадоютая откачала координат щ>иэозрастрйии иточкапокояж, , устойчива. Однако точка покоя может бьггь устойчивой и при немоно» трнном пркбдажрда £ точе* траекторий (например, в случае, когда траектории — эллипсы). Поэтому А. М.Ляпунов вместо функции р рассматривал функции являющиеся в некотором смысле «обобщенным расстоянием» of начала координат. Определение 1.
Функция определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрица-телъной), если в области G где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при Так, в случав п = 3 функции Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению будут знакоположительными, причем здесь величина может быть взята сколь угодно большой. Определение 2.
Функция называется знакопостоянной (положительной или отрицательной), если она в области G может принимать значения только одного определенного знака, но может обращаться в нуль и при . Например, функция будет знакопостоянной (положительной). В самом деле, функцию ) можно представить так: отсюда видно, что она неотрицательна всюду, но обращается в нуль и при , а именно при и любых Х|, XI таких, что Пусть — дифференцируемая функция своих аргументов, и пусть являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1).
Тогда для полной производной функции t; по времени имеем Определение 3. Величина ^, определяемая формулой (3), называется полной производной функции v по времени, составленной в силу системы уравнений (1). Определение 4. Функций .у обладающую свойствами: дифференцируема в некоторой окрестности О начала координат; 3) полная производная £ функции срставденная в силу системы (1), . всюду в П, называют функцией Ляпунова. Теорема 3 (теорема Липуноеа об устойчиюстм).
Если для системы дифференциальных уравнений существует дифференцируемая знакоопределенная функция полная производная J которой по времени, составленная в силу системы (1), есть знакопостоянная функция (знака, противоположного с v) или тождественно обращается в ноль, то точка покоя ) системы (1) устойчива. Приведем идею доказательства.
Возможно вам будут полезны данные страницы:
Пусть для определенности есп» знакоположительная функция, для которой как причем v = 0 лишь при то начало координат есть точка строгого минимума функции хп). В окрестности начала координат поверхности уровня функции v являются, как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае . Так как v0 для малых только для то поверхность в общих чертах напоминает параболоид, вогнутый вверх (рис. 19).
Линии уровня = С представляют собой семейство замкнутых кривых, окружающих начало координат. При этом если то линия уровня целиком лежит внутри области, ограниченной линией v = С2. Зададим е > 0. Придо-статочно малом С линия уровня v = С целиком лежит в £-окрестности начала координат, но не проходит через начало. Следовательно, можно выбрать 6 > 0 такое, что окрестность начала координат целиком лежит внутри области, ограниченной линией v = Су причем в этой окрестности .
Рассмотрим траекторию системы (1), выходящую в начальный момент времени t = to из какой-нибудь точки -окрестнрсти начала координат.
Эта траектория при возрастании t никогда не пересечет ни одной из линий v(x,x2) изнутри наружу. В самом деле, если бы такое пересечение было возможным в какой-нибудь точке, то в этой точке или в ее окрестности функция необходимо имела бы положительную производную t так как при переходе от какой-нибудь линии v = С к другой линии этого семейства, охватывающей первую, функция v(x, х<) возрастает. Но это невозможно в силу того, что по условию .
Значит, если в начальный момент времени какая-нибудь траектория находилась внутри области, ограниченной линией v = С, тоона и в дальнейшем будет все время оставаться внугри этой области. Отсюда ясно, что для всякого е > 0 существует 6 > 0 такое, что любая траектория системы, выходящая в начальный момент времени t = to из ^-окрестности начала координат, для всех t ^ t0 будет содержаться в £-окрестности начала. Это и означает устойчивость точки покоя я, системы (1).
Теорема 4 (теорема Ляпунова об асимптотической устойчивости). Если для системы дифференциальных уравнений существует дифференцируемая знакоопределенная функция , полная производная которой по времени, составленная в силу системы, есть также знакоопреде-ленная функция знака, противоположного с v, то точка покоя п, системы (1) асимптотически устойчива. Пример. Исследовать на устойчивость точку покоя 0(0,0) системы 4
Выберем в качестве функции функцию Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению Эта функция знакоположительная. В силу системы ) найдем Из теоремы 3 следует1, что точка покоя системы устойчива (центр). Асимптотической устойчивости нет, так как траектория системы — окружности. Пример 2. Исследовать на устойчивость точку покоя 0(0,0) системы Беря опять найдем
Таким образом, £ есть знакоотрицательная функция. В силу теоремы 4 точка покоя системы устойчива асимптотически. Теорема 5 (о неустойчивости). Пусть для системы дифференциальных уравнений существует дифференцируемая в окрестности начала координат функция такая, что Если ее полная производная составленная в силу системы (4), есть знакоположительная функция и сколь угодно близко от начала координат имеются точки, в которых функция принимает положительные значения, то точка покоя системы (4) неустойчива.
Пример 3. Исследовать не устойчивость точку покоя системы Возьмем функцию Для нее функция знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, вдоль прямой , то выполнены все условия теоремы 5 и точка покоя неустойчива (седло). Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет.
| В простейших случаях функцию Ляпунова |
можно искать в виде — Устойчивость по первому (линейному) приближению Пусть имеем систему дифференциальных уравнений и пусть естьточка покоя системы, Будем предполагать, что функций дифференцируемы в окрестности начала координат достаточное число раз. Применяя формулу Тейлора, разложим функциипо х в Ькрестности качала координат: или, учитывая (2), где . а слагаемые Я, содержат члены не ниже второго порядка малости относительно .
Система дифференциальных уравнений (1) примет вид Так как понятие устойчивости точки покоя связано с малой окрестностью начала координат в фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по ж. Поэтому наряду с системой (3) рассмотрим систему называемую системой уравнений первого (линейного) приближения для системы (3). Вообще говоря, строгой связи между системами (3) и (4) нет.
Рассмотрим, например, уравнение Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид Решение x(t) = 0 уравнения (6) является устойчивым. Оно же, будучи решением исходного уравнения (5), не является для него устойчивым. В самом деле, каждое действительное решение уравнения (5), удовлетворяющее начальному условию имеет вид и перестает существовать при t = — (решение непродолжаемо вправо). Теорема 6.
Если все корни характеристического уравнения имеют отрицательные действительные части, то точка покоя ,. системы (4) и системы (3) асимптотически устойчива. При выполнении условий теоремы возможно исследование на устойчивость по первому приближению. Теорема 7. Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя ж, = 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению. Наметим идею доказательства теорем 6 и 7. -4 Пусть для простоты корни „ характеристического уравнения (7) — действительные и различные. В этом случае существует такая невырожденная матрица Т с постоянными элементами, что матрица Т-‘AT будет диагональной: Система (3) при том же преобразовании перейдет в систему причем в R< опять входят члены не ниже второго порядка малости относительно Рассмотрим следующие возможности:
Все корни — отрицательные, Положим тогда производная £ в силу системы () будет иметь вид при — малая более высокого порядка, чем квадратичная Таким образом, в достаточно малой окрестности fi точки функция |, знакоположительна, а производная ^f — знакоотрицательна, и, значит, точка покоя асимптотически устойчива. 2. Некоторые из корней (например, положительные, а остальные — отрицательные. Положим тогда Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых .
Что касается производной то, поскольку отрицательны, производная — знакоположительная функция. В силу теоремы 5 точка покоя 0(0,0. 0) неустойчива. В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример 1. Исследовать на устойчивость по первому приближению точку покоя системы Система первого приближения имеет вид Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы Корни характеристического уравнения . Поскольку , нулевое решение системы неустойчиво. Пример 2. Исследуем на устойчивость точку покоя 0(0, 0) системы « Точка покоя системы асимптотически устойчива, так как для этой оистемы функция Ляпунова удовлетворяет условиям теоремы Ляпучора об асимптотической устойчивости. В частности.
В то же время точка покоя системы неустойчива. В самом деле, для функции в силу системы (»») имеем функция знакоположительная. Сколь угодно близко от начала координат 0(0,0) имеются точки, в которых В силу теоремы 5 заключаем о неустойчивости точки покоя 0(0,0) системы (*»). Для системы (*) и (**) система первого приближения одна и та же: Характеристическое уравнение для системы () имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю).
Для системы первого приближения ( качало координат является устойчивой точкой покоя — центром. Системы ) получаются малым возмущением правых частей в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя ) становится асимптотически устойчивой, а для системы (*t) — неустойчивой. Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя. Задам.
Исследовать на устойчивость точку покоя 0(0,0) системы где функция /(х, у) разлагается в сходящийся отеленной ряд и Упражнения Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению Пользуясь определением, исследуйте на устойчивость решения уравнений: Установите характер точки покоя системы и нарисуйте расположение траекторий в окрестности этой точки:
Методом функций Ляпунова исследуйте на устойчивость точку покоя 0(0,0) систем: Исследуйте на устойчивость по первому (линейному) приближению точку покоя 0(0,0) . систем: 1. Асимптотически устойчиво. 2. Неустойчиво. 3. Устойчиво. 4. Устойчивый узел. 5. Седло. 6. Устойчивый фокус. 7. Центр. 8. Асимптотически устойчива, v = 7х2 + у2. 9. Устойчива, v = х2 + у2. 10. Неустойчива, х2 — у2. 11. Асимптотически устойчива. 12. Неустойчива.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Устойчивость 1 ОпределениеСкачать

Digiratory
Видео:Дифференциальные уравнения 7. Устойчивость по Ляпунову. Асимптотическая устойчивостьСкачать

Лаборатория автоматизации и цифровой обработки сигналов
Видео:Матричный метод решения систем уравненийСкачать

Устойчивость нелинейных систем
Анализ устойчивости систем является одним из важнейших этапов проектирования систем управления, однако при анализе нелинейных, строго говоря, нет метода отвечающего критериям необходимости и достаточности, а критерии являются, как правило только достаточным (для устойчивости). Исходя из этого, для некоторых систем невозможно однозначно говорить о неустойчивости.
В классической теории управления имеется два основных аналитических метода: первый и второй методы Ляпунова, а также достаточно большое количество модификаций второго метода, как не связанного с линеаризацией.
Рассмотрим применение классических методов Ляпунова.
Видео:Функция Ляпунова 2 ПримерыСкачать
Первый метод Ляпунова
Позволяет судить об устойчивости положения равновесия по линеаризованным уравнениям. Метод основан на утверждениях:
- если собственные значения линеаризованной системы имеют отрицательные действительные части (линеаризованная система асимптотически устойчива), то положение равновесия нелинейной системы устойчиво «в малом»;
- если среди собственных значений линеаризованной системы имеются «правые», то положение равновесия нелинейной системы неустойчиво;
- если имеются некратные собственные значения на мнимой оси, а остальные — «левые», то в этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.
Таким образом для анализа системы по первому методу Ляпунова необходимо:
- Найти положение равновесия системы — движений в системе нет (т.е. скорости и ускорения равны нулю) [ frac <mathrmv_><mathrmt>= ]
- Линеаризовать систему в окрестности точки равновесия
- Записать полученное линеаризованное дифференциальное уравнение в матричной форме (составить матрицу А)
- Составить характеристический полином линеаризованной системы: [ = ]
- Найти корни характеристического полинома. По виду корней сделать заключение о характере процессов в системе.
Основными недостатками первого метода Ляпунова являются:
- Если имеется корень на мнимой оси, то невозможно сказать о поведении процессов в системе.
- Возможно говорить только об устойчивости «в малом», т.е. при больших отклонениях от положения равновесия система может быть неустойчивой.
Пример 1.
Исследуем систему описываемую дифференциальными уравнениями:
Шаг 1. Положение равновесия:
Для нахождения точек равновесия левые части уравнений приравниваются к 0, что эквивалентно тому, что переменные состояния являются константами, а все их производные равны 0.
Шаг 2. Линеаризация для малых отклонений
Для линеаризации малых отклонений в точке равновесия старшие степени переменных, входящих в уравнения принимаются равными нулю.
Шаг 3. Линеаризованное управление в матричной форме
Преобразуем полученную линейную систему уравнений в матричный вид.
Шаг 4. Характеристический полином
Шаг 5. Корни характеристического полинома
Приравниваем характеристический полином к 0 и находим корни уравнения.
Заключение об устойчивости системы
в данном примере при линеаризации система имеет два корня с отрицательной вещественной частью, т.е. мы можем сказать, что система устойчива «в малом» (при больших отклонениях система может быть неустойчива).
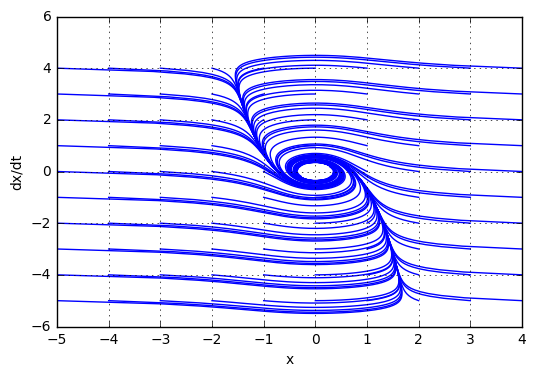
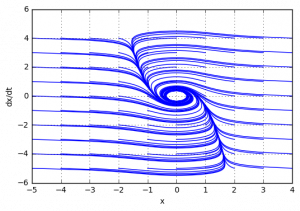
Подтвердим теоретический вывод компьютерным моделированием (построением фазового портрета)
При этом, при начальных условиях, находящиеся дальше от точки равновесия, система становится неустойчивой
Пример 2. Нелинейный осциллятор
В качестве второго примера рассмотрим нелинейный осцилятор описываемый системой дифференциальных уравнений:
Аналогично первому примеру выполняем последовательность шагов
Шаг 1. Положение равновесия:
Шаг 2. Линеаризация для малых отклонений
Шаг 3. Линеаризованное управление в матричной форме
Шаг 4. Характеристический полином
Шаг 5. Корни характеристического полинома
Заключение об устойчивости системы
Рассматриваемая система является критическим случаем о ее устойчивости невозможно судить по линеаризованным уравнениям, применяемым в первом методе Ляпунова.
Видео:№11. Понятие устойчивости. Общая постановка задачи устойчивости по А.М.Ляпунову.Скачать

Второй метод Ляпунова
Второй метод Ляпунова не связан с линеаризацией системы, поэтому также называется прямым методом.
Для начала необходимо ввести понятия знакоопределенной, знакопостоянной и знакопеременной функций. Пусть имеется функция нескольких переменных:
Функция (V ) называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат
[ left ( Vleft ( bar right )=0 right ) ]
Функция (V ) называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Функция (V ) называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.
Теорема Ляпунова об устойчивости нелинейных систем
Если при заданных в форме
уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова
чтобы ее производная по времени
тоже была знакоопределенной (или знакопостоянной), но имела знак противоположный знаку (V), то данная система устойчива.
Для упрощения скажем, что функция Ляпунова должна быть положительной знакоопределенной функцией. Тогда условия теоремы Ляпунова будут выглядеть следующим образом:
Для устойчивости положения равновесия достаточно существования дифференцируемой функции
называемой функцией Ляпунова, удовлетворяющей в окрестности начала координат следующим условиям:
- (Vleft ( v_, v_,…, v_right ) geq 0) причем (V=0) лишь при следующем условии, означающем что функция (V) имеет строгий минимум в начале координат. [ bar= begin v_ \ vdots \ v_ end = bar ]
- Производная функции по времени [ frac <mathrmVleft ( bar right )><mathrmt>=sum_^frac<partial v_>frac <mathrmv_><mathrmt>=begin frac<partial v_> & frac<partial v_> & cdots & frac<partial v_>endbeginfrac <mathrmv_><mathrmt>\ frac <mathrmv_><mathrmt>\ vdots \ frac <mathrmv_><mathrmt>end ] в силу дифференциального уравнения (frac <mathrmbar><mathrmt>=barleft ( bar right ) ) является отрицательной знакопостоянной функцией, т.е. [ frac <mathrmVleft ( bar right )><mathrmt>=gradbarcdot frac <mathrmbar><mathrmt>=gradbarcdot barleft ( bar right )leq 0 ] при (tgeq t_)
Таким образом, условия:
- (frac <mathrmVleft ( bar right )><mathrmt>leq 0) и функция (Vleft ( v_, v_,…, v_right ) ) является положительной знакоопределенной — это является достаточным условием устойчивости
- (frac <mathrmVleft ( bar right )><mathrmt> ) — отрицательно определенная — это является достаточным условием асимптотической устойчивости.
- (left | v right |rightarrow infty : frac <mathrmVleft ( bar right )><mathrmt>rightarrow infty ) — достаточное условие устойчивости «в целом».
Для анализа системы по второму методу Ляпунова необходимо:
- Выбрать функцию Ляпунова от n переменных, где n- порядок системы.
- Найти частные производные по переменным.
- Вычислить производную функции по времени (frac <mathrmVleft ( bar right )><mathrmt>). Проанализировать полученный знак производной.
Из-за того, что второй метод Ляпунова не связан с линеаризацией, он считается универсальным. Однако он имеет ряд недостатков:
- Нет общих требований по выбору функции V
- Достаточный характер утверждения (если условия не выполняются, то об устойчивости ничего сказать нельзя, а можно посоветовать подобрать другую функцию (V ))
Пример 3. Нелинейный осциллятор
Проанализируем систему из примера (2).
Шаг 1. Функция Ляпунова
Для начала необходимо выбрать функцию Ляпунова от 2-х переменных (т.к. два вектора состояния):
Шаг 2. Частные производные
Шаг 3. Производная функции
Подставим в выражение значения исходя из ДУ:
Заключение об устойчивости системы
Исследовав систему первым методом Ляпунова мы не смогли сделать конкретный вывод об устойчивости системы, что позволил нам сделать второй метод Ляпунова. В результате мы можем сделать вывод, что система является асимптотически устойчивой.
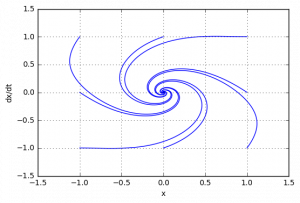
Аналогично проверим с помощью моделирования:
Пример 4.
Рассмотрим систему, описываемую следующей системой дифференциальных уравнений:
Очевидно, что применение первого метода Ляпунова невозможно, т.к. матрица А состоит из нулей, а, следовательно, собственные значения равны нулю. Поэтому применим второй метод Ляпунова:
Шаг 1. Функция Ляпунова
Выбор функции Ляпунова второго порядка
Шаг 2. Частные производные
Шаг 3. Производная функции
При (a=3) имеет место асимптотическая устойчивость.
Заключение об устойчивости системы
Система является устойчивой.
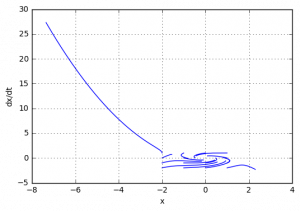
Фазовый портрет системы выглядит следующим образом:
📽️ Видео
Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Решение системы линейных уравнений методом исключения | МатематикаСкачать

Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Устойчивость по ЛяпуновуСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Линейная Алгебра. Алексей Савватеев и Александр Тонис. Лекция 5.1. Системы линейных уравнений 3x3Скачать

3 Второй метод ЛяпуноваСкачать

Семинар "Использование метода функций Ляпунова"Скачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Пояснение определения устойчивости по ЛяпуновуСкачать

ДУ 6 Теория устойчивостиСкачать

Козлов В.В. - Формальная устойчивость и неустойчивость по Ляпунову в аналитических системахСкачать