Уравнение ляпунова для анализа свойства устойчивости линейных дискретных систем

Видео:Устойчивость 1 ОпределениеСкачать

Уравнение Ляпунова и критерий Ляпунова устойчивости линейных систем.

Рассмотрим линейную систему

где х — вектор (х € # п ), А — квадратная матрица n-го порядка. Пусть задана квадратичная форма tu(x) = х г Сх. Для того чтобы эта квадратичная форма была равна производной но времени от квадратичной формы У(х) = х т Вх в силу системы (4.21), т. е. У(х) =-ш(х), матрица В должна удовлетворять матричному уравнению

Действительно, производная по времени от квадратичной формы У(х) = х т Вх в силу уравнения (4.21) имеет вид

Отсюда следует, что равенство /(х) = w(x) возможно в том и только том случае, если матрицы В и С удовлетворяют уравнению (4.22), которое называется уравнением Ляпунова. Таким образом, чтобы по заданной квадратичной форме tu(x) = х т Сх найти соответствующую ей квадратичную форму К(х) = х т ?х, нужно решить уравнение Ляпунова.

Исследование уравнения Ляпунова представляет большой интерес, так как это уравнение позволяет найти функцию Ляпунова в виде квадратичной формы по заданной ее производной. Естественно возникает вопрос: когда уравнение Ляпунова имеет решение? Ответ на этот вопрос зависит от того, какие корни имеет характеристическое уравнение системы (4.21)

Теорема 4.14 (теорема о существовании решения уравнения Ляпунова). Если среди корней характеристического уравнения (4.23) нет пари корней, сумма которых равна нулю, т. е. Aj + Xj ф 0 при всех i, j = 1,2. п, то при любой симметрической матрице С уравнение Ляпунова имеет единственное решение для неизвестной матрицы В.

Эта теорема может быть доказана с помощью теории операторов [7], и ее доказательство здесь не рассматривается.

Теорема 4.15 (критерий устойчивости Ляпунова линейных систем). Для того чтобы линейная стационарная система (4.21) была асимптотически устойчива, необходимо и достаточно, чтобы для любой отрицательно определенной квадратичной формы w(x) = = х Т Сх существовала положительно определенная квадратичная форма V(x) = х Т Вх такая, что производная по времени от этой функции в силу уравнения системы (4.21) равна заданной квадратичной форме щ(х): У(х) = w(x).

Доказательство. Необходимость. Существование некоторой квадратичной формы У(х) = х Т Вх, производная от которой по времени равна заданной квадратичной форме, следует из теоремы 4.14. Поэтому достаточно показать, что эта квадратичная форма является положительно определенной функцией.

Пусть система (4.21) устойчива. Тогда ее решение, которое при начальном условии х(0) = х° имеет вид (см. (1.10)) х(?) = е^х 0 , стремится к нулю при t —> оо. Следовательно, и квадратичная форма V(x(?)) —» 0 при ? —> оо. Покажем, что квадратичная функция, удовлетворяющая условиям теоремы, является положительно определенной функцией. Допустим противное: в некоторой точке х = х° ф О квадратичная форма К(х°) ^ 0. Тогда в силу того, что

где x(t) = e At x°_y функция V(x(t)) при t > 0 отрицательна и убывает с ростом t. А это противоречит тому, что К(х(?)) —> 0 при t —> оо.

Достаточность непосредственно следует из теоремы Ляпунова об асимптотической устойчивости.

Теорема 4.16 (теорема о существовании положительно определенного решения уравнения Ляпунова). Если матрица Л устойчива, т. е. все ее собственные значения имеют отрицательные вещественные части, то, какова бы ни была отрицательно определенная матрица С, уравнение Ляпунова (4.22) имеет единственное решение В, которое является положительно определенной матрицей.

Эта теорема непосредственно вытекает из теорем 4.14 и 4.15.

Теорема 4.17. Если среди корней характеристического уравнения системы (4.21) имеется хотя бы один корень с положительной вещественной частью и сумма никаких пар этих корней не обращается в нуль, то, какова бы ни была положительно определенная функция w(x), найдется квадратичная форма V(x), у которой производная по времени в силу указанного уравнения системы удовлетворяет уравнению 1/(х) = w(x), и в любой окрестности начала координат имеется точка, в которой V(х) принимает положительное значение.

Доказательство. Существование квадратичной формы К(х), удовлетворяющей указанному в теореме уравнению, следует из теоремы 4.14. Покажем, что в любой окрестности начала координат существует точка, в которой V(x) принимает положительное значение.

Квадратичная форма К( х ) не может быть отрицательно определенной, так как в противном случае функция — V(x) удовлетворяла бы условию теоремы Ляпунова об асимптотической устойчивости. В силу указанной причины в любой окрестности начала координат существует точка, где V(x) по крайней мере обращается в нуль. Но так как V'(x) = w(x) > 0, то в любой окрестности такой точки существует точка, где V(х) > 0.

Теорема 4.18. Если среди корней характеристического уравнения системы (4.21) имеется хотя бы один корень с положительной вещественной частью, то, какова бы ни была положительно определенная квадратичная форма w(x), всегда найдутся квадратичная форма V (х) и положительное число а такие, что производная V (х) в силу указанного уравнения системы удовлетворяет соотношению

и в любой окрестности начала координат найдется точка, в которой квадратичная форма V(х) принимает положительное значение.

Доказательство. Рассмотрим наряду с (4.21) систему

Характеристическое уравнение этой системы имеет вид

и его корни Ai связаны с корнем Ai характеристического уравнения системы (4.21) соотношением А* = + а/2.

Пусть Ai₀ — корень с положительной вещественной частью. Выберем а таким, чтобы выполнялись условия:

• 1) из ReAj₀ > 0 следует ReA;₀ > 0;
• 2) А* + А^ ф 0 при всех г и А;.

Условие 1) всегда можно выполнить, выбрав а достаточно малым. Учитывая, что А* + А* = Aj + А* — а, можно выбрать а, не совпадающим ни с одной суммой А* + А*.

Согласно теореме 4.17 для положительно определенной функции найдется квадратичная форма V(x), принимающая в какой-либо точке любой окрестности начала координат положительное значение, и производная по времени этой формы в силу уравнения (4.24) равна w(x):

Так как Лх — производная по времени квадратичной формы V(x) в силу уравнения (4.21) и в случае квадратичной формы

Видео:Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

Digiratory

Видео:№11. Понятие устойчивости. Общая постановка задачи устойчивости по А.М.Ляпунову.Скачать

Лаборатория автоматизации и цифровой обработки сигналов

Видео:Теория автоматического управления. Лекция 8. Дискретные САУ. Аналог критерия устойчивости МихайловаСкачать

Устойчивость нелинейных систем

Анализ устойчивости систем является одним из важнейших этапов проектирования систем управления, однако при анализе нелинейных, строго говоря, нет метода отвечающего критериям необходимости и достаточности, а критерии являются, как правило только достаточным (для устойчивости). Исходя из этого, для некоторых систем невозможно однозначно говорить о неустойчивости.

В классической теории управления имеется два основных аналитических метода: первый и второй методы Ляпунова, а также достаточно большое количество модификаций второго метода, как не связанного с линеаризацией.

Рассмотрим применение классических методов Ляпунова.

Видео:Функция Ляпунова 1 Теорема ЛяпуноваСкачать

Первый метод Ляпунова

Позволяет судить об устойчивости положения равновесия по линеаризованным уравнениям. Метод основан на утверждениях:

• если собственные значения линеаризованной системы имеют отрицательные действительные части (линеаризованная система асимптотически устойчива), то положение равновесия нелинейной системы устойчиво «в малом»;
• если среди собственных значений линеаризованной системы имеются «правые», то положение равновесия нелинейной системы неустойчиво;
• если имеются некратные собственные значения на мнимой оси, а остальные — «левые», то в этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.

Таким образом для анализа системы по первому методу Ляпунова необходимо:

1. Найти положение равновесия системы — движений в системе нет (т.е. скорости и ускорения равны нулю) [ frac <mathrmv_><mathrmt>= ]
2. Линеаризовать систему в окрестности точки равновесия
3. Записать полученное линеаризованное дифференциальное уравнение в матричной форме (составить матрицу А)
4. Составить характеристический полином линеаризованной системы: [ = ]
5. Найти корни характеристического полинома. По виду корней сделать заключение о характере процессов в системе.

Основными недостатками первого метода Ляпунова являются:

• Если имеется корень на мнимой оси, то невозможно сказать о поведении процессов в системе.
• Возможно говорить только об устойчивости «в малом», т.е. при больших отклонениях от положения равновесия система может быть неустойчивой.

Пример 1.

Исследуем систему описываемую дифференциальными уравнениями:

Шаг 1. Положение равновесия:

Для нахождения точек равновесия левые части уравнений приравниваются к 0, что эквивалентно тому, что переменные состояния являются константами, а все их производные равны 0.

Шаг 2. Линеаризация для малых отклонений

Для линеаризации малых отклонений в точке равновесия старшие степени переменных, входящих в уравнения принимаются равными нулю.

Шаг 3. Линеаризованное управление в матричной форме

Преобразуем полученную линейную систему уравнений в матричный вид.

Шаг 4. Характеристический полином

Шаг 5. Корни характеристического полинома

Приравниваем характеристический полином к 0 и находим корни уравнения.

Заключение об устойчивости системы

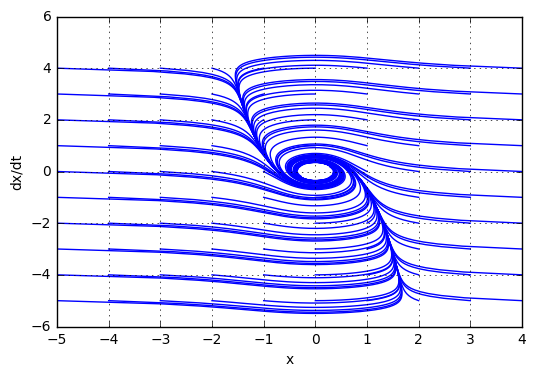
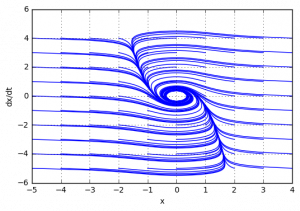
в данном примере при линеаризации система имеет два корня с отрицательной вещественной частью, т.е. мы можем сказать, что система устойчива «в малом» (при больших отклонениях система может быть неустойчива).

Подтвердим теоретический вывод компьютерным моделированием (построением фазового портрета)

При этом, при начальных условиях, находящиеся дальше от точки равновесия, система становится неустойчивой

Пример 2. Нелинейный осциллятор

В качестве второго примера рассмотрим нелинейный осцилятор описываемый системой дифференциальных уравнений:

Аналогично первому примеру выполняем последовательность шагов

Шаг 1. Положение равновесия:

Шаг 2. Линеаризация для малых отклонений

Шаг 3. Линеаризованное управление в матричной форме

Шаг 4. Характеристический полином

Шаг 5. Корни характеристического полинома

Заключение об устойчивости системы

Рассматриваемая система является критическим случаем о ее устойчивости невозможно судить по линеаризованным уравнениям, применяемым в первом методе Ляпунова.

Видео:Теория автоматического управления. Лекция 8. Основы устойчивостиСкачать

Второй метод Ляпунова

Второй метод Ляпунова не связан с линеаризацией системы, поэтому также называется прямым методом.

Для начала необходимо ввести понятия знакоопределенной, знакопостоянной и знакопеременной функций. Пусть имеется функция нескольких переменных:

Функция (V ) называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат

[ left ( Vleft ( bar right )=0 right ) ]

Функция (V ) называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Функция (V ) называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Теорема Ляпунова об устойчивости нелинейных систем

Если при заданных в форме

уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова

чтобы ее производная по времени

тоже была знакоопределенной (или знакопостоянной), но имела знак противоположный знаку (V), то данная система устойчива.

Для упрощения скажем, что функция Ляпунова должна быть положительной знакоопределенной функцией. Тогда условия теоремы Ляпунова будут выглядеть следующим образом:

Для устойчивости положения равновесия достаточно существования дифференцируемой функции

называемой функцией Ляпунова, удовлетворяющей в окрестности начала координат следующим условиям:

1. (Vleft ( v_, v_,…, v_right ) geq 0) причем (V=0) лишь при следующем условии, означающем что функция (V) имеет строгий минимум в начале координат. [ bar= begin v_ \ vdots \ v_ end = bar ]
2. Производная функции по времени [ frac <mathrmVleft ( bar right )><mathrmt>=sum_^frac<partial v_>frac <mathrmv_><mathrmt>=begin frac<partial v_> & frac<partial v_> & cdots & frac<partial v_>endbeginfrac <mathrmv_><mathrmt>\ frac <mathrmv_><mathrmt>\ vdots \ frac <mathrmv_><mathrmt>end ] в силу дифференциального уравнения (frac <mathrmbar><mathrmt>=barleft ( bar right ) ) является отрицательной знакопостоянной функцией, т.е. [ frac <mathrmVleft ( bar right )><mathrmt>=gradbarcdot frac <mathrmbar><mathrmt>=gradbarcdot barleft ( bar right )leq 0 ] при (tgeq t_)

Таким образом, условия:

1. (frac <mathrmVleft ( bar right )><mathrmt>leq 0) и функция (Vleft ( v_, v_,…, v_right ) ) является положительной знакоопределенной — это является достаточным условием устойчивости
2. (frac <mathrmVleft ( bar right )><mathrmt> ) — отрицательно определенная — это является достаточным условием асимптотической устойчивости.
3. (left | v right |rightarrow infty : frac <mathrmVleft ( bar right )><mathrmt>rightarrow infty ) — достаточное условие устойчивости «в целом».

Для анализа системы по второму методу Ляпунова необходимо:

1. Выбрать функцию Ляпунова от n переменных, где n- порядок системы.
2. Найти частные производные по переменным.
3. Вычислить производную функции по времени (frac <mathrmVleft ( bar right )><mathrmt>). Проанализировать полученный знак производной.

Из-за того, что второй метод Ляпунова не связан с линеаризацией, он считается универсальным. Однако он имеет ряд недостатков:

• Нет общих требований по выбору функции V
• Достаточный характер утверждения (если условия не выполняются, то об устойчивости ничего сказать нельзя, а можно посоветовать подобрать другую функцию (V ))

Пример 3. Нелинейный осциллятор

Проанализируем систему из примера (2).

Шаг 1. Функция Ляпунова

Для начала необходимо выбрать функцию Ляпунова от 2-х переменных (т.к. два вектора состояния):

Шаг 2. Частные производные

Шаг 3. Производная функции

Подставим в выражение значения исходя из ДУ:

Заключение об устойчивости системы

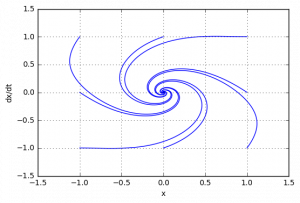
Исследовав систему первым методом Ляпунова мы не смогли сделать конкретный вывод об устойчивости системы, что позволил нам сделать второй метод Ляпунова. В результате мы можем сделать вывод, что система является асимптотически устойчивой.

Аналогично проверим с помощью моделирования:

Пример 4.

Рассмотрим систему, описываемую следующей системой дифференциальных уравнений:

Очевидно, что применение первого метода Ляпунова невозможно, т.к. матрица А состоит из нулей, а, следовательно, собственные значения равны нулю. Поэтому применим второй метод Ляпунова:

Шаг 1. Функция Ляпунова

Выбор функции Ляпунова второго порядка

Шаг 2. Частные производные

Шаг 3. Производная функции

При (a=3) имеет место асимптотическая устойчивость.

Заключение об устойчивости системы

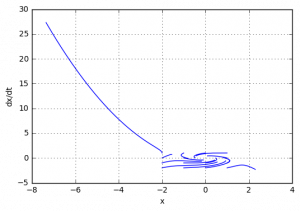
Система является устойчивой.

Фазовый портрет системы выглядит следующим образом:

Видео:Дифференциальные уравнения 7. Устойчивость по Ляпунову. Асимптотическая устойчивостьСкачать

Устойчивость по Ляпунову: основные понятия и определения

Пусть имеем систему дифференциальных уравнений

Решение , системы (1), удовлетворяющее начальным условиям , называется устойчивым no Ляпунову при , если для любого 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> существует 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAWCAMAAABKfhpBAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAQjHgIRHRwaZc8IGRQXGCR+L2IgAAAVVJREFUOMutVNuWwyAINN4Ab+H/v3YjamPitj3bbp4slYGZAZX6x8/qfkh5ioL+G8oOgbEeYprDGtz73Pyo5UA5rADZXPMKvAPRBtEMoNCzgW63wvZGjFCUomDbLy+M1MZ3Eulsx6JdYRJLsS4FsbSBC4cZOAMuknsvJEzThlho+TgKezZydjzTzAg3kiyFgZtMMYlRXLpsacvRN3HiVQu8yjdgXJPJ8ZFludWaRYB0FxX9CZQHzJGIlRmEKkSHoRLHVVgtd/sDyJ0wllO/PmB274dKv8LEs5+T1CYqGtFGYAjnfcAXIEdac+qgojlXWexD4st8mPhcmXpXPBJ/KgFZhW44UtuP1jVdfboZruv/uTaitEdAd86sNgF80H387DR+sK4GmVJCL+Xc8K8dctl6JPnXy3CEiZb4upr0yeu1mVvL8NkrWC5Da4398DVF+uIR/f77AQOYCjg2wpU7AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> такое, что для всякого решения , системы (1), начальные значения которого удовлетворяют условиям

имеют место неравенства

Если при сколь угодно малом 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» /> хотя бы для одного решения , неравенства (3) не выполняются, то решение называется неустойчивым .

Если, кроме выполнения неравенств (3) при условии (2) выполняется также условие

то решение , называется асимптотически устойчивым .

Исследование на устойчивость решения , системы (1) можно свести к исследованию на устойчивость нулевого (тривиального) решения , некоторой системы, аналогичной системе (1),

Говорят, что точка , есть точка покоя системы (1′).

Применительно к точке покоя определения устойчивости и неустойчивости могут быть сформулированы так. Точка покоя , устойчива по Ляпунову , если, каково бы ни было 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» />, можно найти такое 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» />, что для любого решения , начальные данные которого , удовлетворят условию

Для случая геометрически это означает следующее. Каким бы малым ни был радиус цилиндра с осью , в плоскости найдется δ-окрестность точки такая, что все интегральные кривые , выходящие из этой окрестности, для всех будут оставаться внутри этого цилиндра (рис. 30).

Если кроме выполнения неравенств (3), выполняется также условие , то устойчивость асимптотическая .

Точка покоя , неустойчива , если при сколь угодно малом 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» /> хотя бы для одного решения , условие (3′) не выполняется.

Пример 1. Исходя из определения устойчивости по Ляпунову, исследовать на устойчивость решение уравнения, удовлетворяющее начальному условию

Решение. Уравнение (5) есть линейное неоднородное уравнение. Его общее решение . Начальному условию удовлетворяет решение

уравнения (5). Начальному условию удовлетворяет решение

Рассмотрим разность решений (7) и (6) уравнения (5) и запишем ее так:

Отсюда видно, что для всякого 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> существует 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» /> (например, ) такое, что для всякого решения уравнения (5), начальные значения которого удовлетворяют условию , выполняется неравенство

для всех . Следовательно, решение является устойчивым. Более того, поскольку

решение является асимптотически устойчивым.

Это решение является неограниченным при .

Приведенный пример показывает, что из устойчивости решения дифференциального уравнения не следует ограниченности решения.

Пример 2. Исследовать на устойчивость решение уравнения

Решение. Оно имеет очевидные решения

Интегрируем уравнение (8): , или , откуда

Все решения (9) и (10) ограничены на . Однако решение неустойчиво при , так как при любом имеем (рис.31).

Следовательно, из ограниченности решений дифференциального уравнения , вообще говоря, не следует их устойчивости . Это явление характерно для нелинейных уравнений и систем.

Пример 3. Исходя из определения устойчивости по Ляпунову, показать, что решение системы, удовлетворяющее начальным условиям , устойчиво

Решение. Решение системы (11), удовлетворяющее заданным начальным условиям, есть . Любое решение этой системы, удовлетворяющее условиям , имеет вид

Возьмем произвольное 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> и покажем, что существует 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAWCAMAAABKfhpBAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAQjHgIRHRwaZc8IGRQXGCR+L2IgAAAVVJREFUOMutVNuWwyAINN4Ab+H/v3YjamPitj3bbp4slYGZAZX6x8/qfkh5ioL+G8oOgbEeYprDGtz73Pyo5UA5rADZXPMKvAPRBtEMoNCzgW63wvZGjFCUomDbLy+M1MZ3Eulsx6JdYRJLsS4FsbSBC4cZOAMuknsvJEzThlho+TgKezZydjzTzAg3kiyFgZtMMYlRXLpsacvRN3HiVQu8yjdgXJPJ8ZFludWaRYB0FxX9CZQHzJGIlRmEKkSHoRLHVVgtd/sDyJ0wllO/PmB274dKv8LEs5+T1CYqGtFGYAjnfcAXIEdac+qgojlXWexD4st8mPhcmXpXPBJ/KgFZhW44UtuP1jVdfboZruv/uTaitEdAd86sNgF80H387DR+sK4GmVJCL+Xc8K8dctl6JPnXy3CEiZb4upr0yeu1mVvL8NkrWC5Da4398DVF+uIR/f77AQOYCjg2wpU7AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> такое, что при имеют место неравенства

Это и будет означать, согласно определению, что нулевое решение системы (11) устойчиво по Ляпунову. Имеем, очевидно,

для всех . Поэтому, если то и подавно

Следовательно, если, например, взять , то при и в силу (12) будут иметь место неравенства (13) для всех , т.е. действительно нулевое решение системы (11) устойчиво по Ляпунову , но эта устойчивость не асимптотическая.

Теорема. Решения системы линейных дифференциальных уравнений

либо все одновременно устойчивы, либо неустойчивы.

Это предложение не верно для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.

Пример 4. Исследовать на устойчивость решение нелинейного уравнения

Решение. Оно имеет очевидные решения и .

Решение этого уравнения неустойчиво, а решение является асимптотически устойчивым. В самом деле, при все решения уравнения (14)

💥 Видео

Устойчивость по ЛяпуновуСкачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Структуры Льюиса и формальный зарядСкачать

ДУ 6 Теория устойчивостиСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Устойчивость регулированияСкачать

Теория автоматического управления. Лекция 19. Критерий РаусаСкачать

Теория автоматического управления. Лекция 9. Критерий ГурвицаСкачать

Олег Тиньков в МГУСкачать

24) УСТОЙЧИВОСТЬ. ПОНЯТИЕ УСТОЙЧИВОСТИ. ОСНОВНЫЕ СВЕДЕНИЯ. ЧАСТЬ I.Скачать

Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

Устойчивость. Лекция 1. ТеорияСкачать