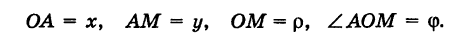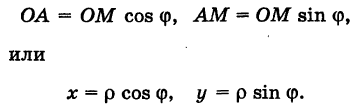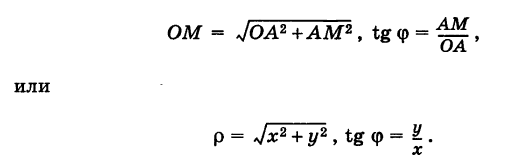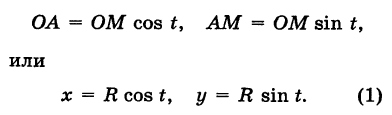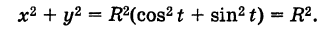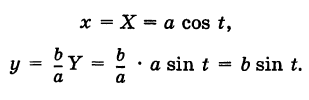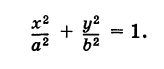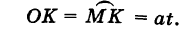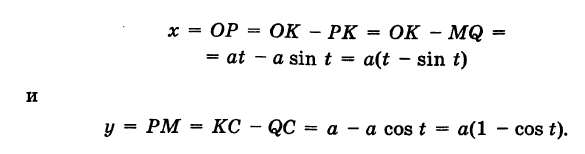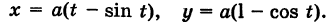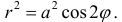По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса 





Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «прорисовывает» линию.
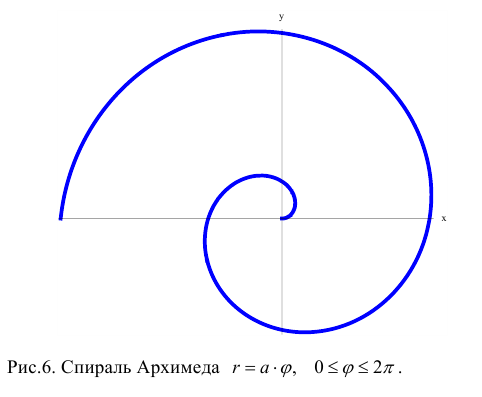
«Дежурным» примером полярной кривой является Архимедова спираль 




В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен 

! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже
Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.
Сначала простейшие уравнения и простейшие линии:
Уравнение вида задаёт луч, исходящий из полюса. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?
Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс.
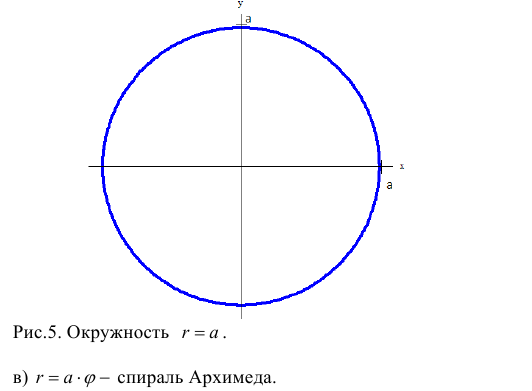
Уравнение вида 

Например, 

Возведём обе части в квадрат:

А теперь оценИте удобство – с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения 
Рассмотрим более содержательные задачи на построение:
Задача 116
Построить линию
Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство 
я советую более быстрый графический метод решения:
– Посмотрим на график функции 






В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла.
Для бОльшей ясности к отрицательным значениям угла я буду «прикручивать» один оборот (левая колонка), и в силу чётности косинуса 
Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной ранее технологии: 
В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы 
Обе части уравнения 

Выделяя полный квадрат, приводим уравнение к понятному виду: 


Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность 😉
Почему мы не рассмотрели значения угла вне промежутка 
Ответ прост: нет смысла. Ввиду периодичности функции 
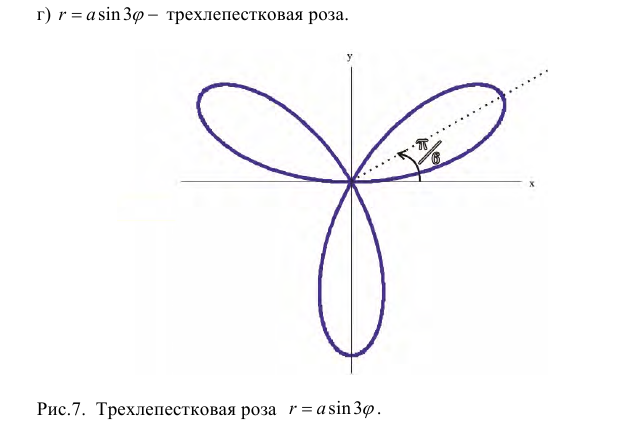
Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида 


Образно говоря, все такие окружности «сидят» на полярной оси 

Похожая задача для самостоятельного решения:
Задача 117
Построить линию 
Систематизируем порядок решения задачи:
Находим область определения функции, для этого удобно посмотреть на синусоиду (Приложение Тригонометрия), чтобы сразу же понять, где синус неотрицателен.
На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?
На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.
И, наконец, находим уравнение линии в декартовой системе координат.
Примерный образец решения в конце книги.
Общий алгоритм и технику построения в полярных координатах мы детализируем и существенно ускорим совсем скоро, но перед этим познакомимся ещё с одной распространённой линией:
- Полярные координаты — определение и вычисление с примерами решения
- Полярные координаты. параметрические уравнения линии
- Полярные координаты
- Связь между прямоугольными и полярными координатами
- Параметрические уравнения линии
- Параметрические уравнения циклоиды
- Полярная система координат
- Полярная система координат
- 💥 Видео
Видео:Построение кривой в полярной системе координатСкачать

Полярные координаты — определение и вычисление с примерами решения
Содержание:
Видео:Полярная система координатСкачать

Полярные координаты. параметрические уравнения линии
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
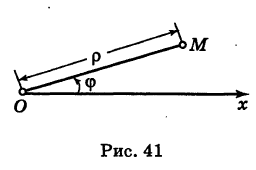
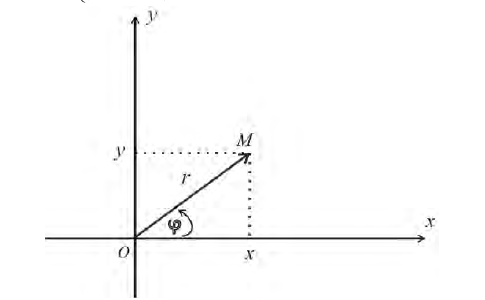
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
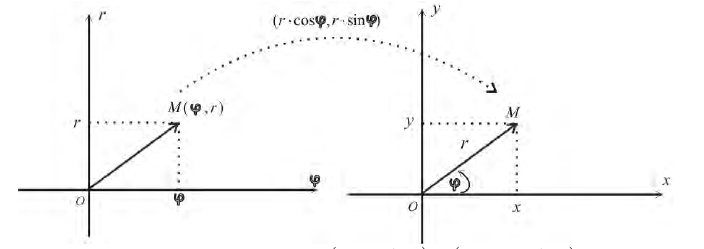
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 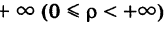
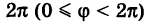
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
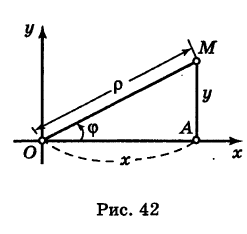
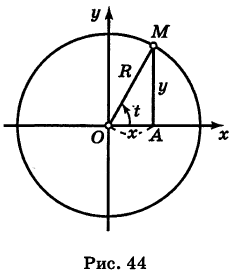
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
Тогда для произвольной точки М имеем
Считая угол ф острым, из прямоугольного треугольника АОМ находим
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
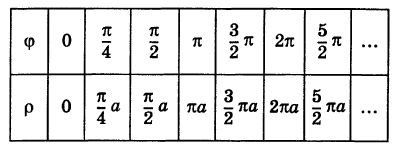
Пример:
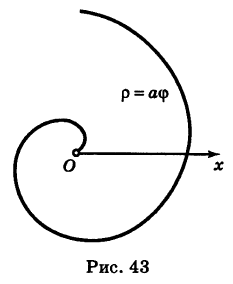
Рассмотрим кривую 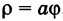
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 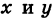
Пример:
Выведем параметрические уравнения окружности.
Пусть М 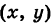
Это и есть параметрические уравнения окружности.
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где
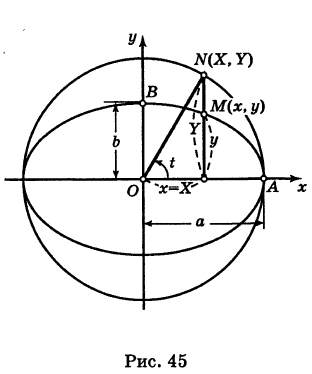
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
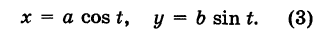
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:
Решение:
Составляем таблицу значений:
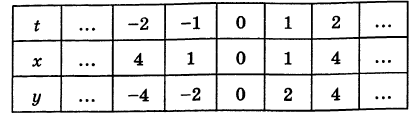
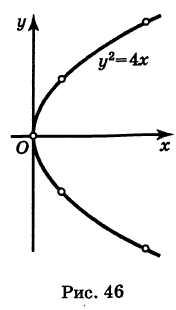
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 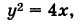
Параметрические уравнения циклоиды
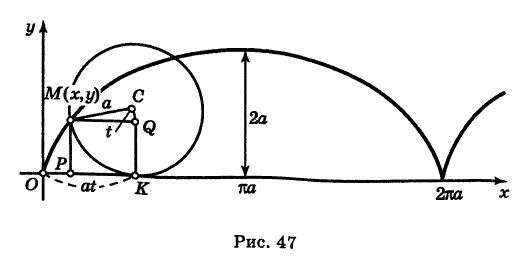
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
Таким образом, параметрические уравнения циклоиды есть
Полярная система координат
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 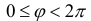
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 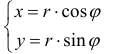
Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
Пример 1.
Построим на плоскости линию, заданную уравнением:
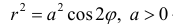
Решение.
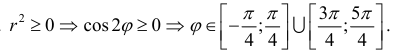
Вычислим значения r при различных значениях ϕ : 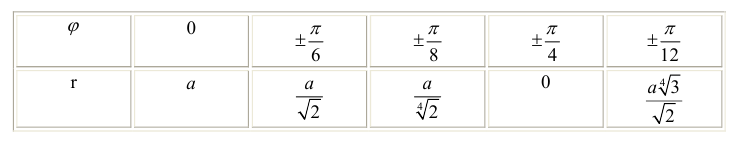
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
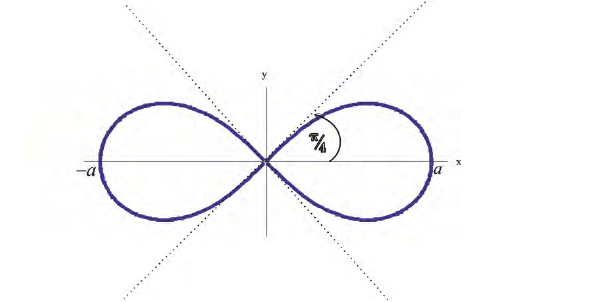
Рис.3. Лемниската
Пример 2.
а) Построим кривую 
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
При этом, если r > 0, то векторы 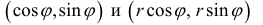
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Полярная система координат
Для определения положения точки на плоскости можно пользоваться и другими системами координат. В частности широко используется полярная система координат. На плоскости выберем точку и обозначим ее О. Рассмотрим луч с началом в О, а на луче выберем единичный отрезок ОЕ. Точка О называется полюсом, а луч ОЕ называется полярной осью. Положение любой точки М на плоскости, отличной от О определяется парой чисел: расстоянием r = |OM| и величиной угла между лучами ОЕ и ОМ, причем угол ориентирован, т. е. положительное направление против часовой стрелки, а отрицательное – по часовой стрелке. Для точки О считаем r = 0, а угол j не определен.
Для рассматриваемых полярных координат мы имеем r ³ 0, а j Î R. Однако, в нашем случае пары чисел (r, j) и (r, j + 2 
Например, пара чисел (−3; 

Пример 1. Найдем уравнение прямой, не проходящей через полюс О. Зададим эту прямую числом р, длиной отрезка ОР и углом a, где Р – основание перпендикуляра ОР на прямую, а a –ориентированный угол между лучом ОР и полярной осью.
Если произвольная точка М(r, j) принадлежит данной прямой, то р = rcos (j −a) и обратно.
Поэтому имеем уравнение прямой: 
Пример 2. Луч 
Решение. Примем за полярную систему координат начальное положение луча 






Рассмотрим согласованную с полярной системой координат прямоугольную декартовую систему. Известна связь между координатами этих систем.

Заменяя полярные координаты, получим параметрические уравнения траектории точки М:
РЕШЕНИЕ НУЛЕВОГО ВАРИАНТА
КОНТРОЛЬНОЙ РАБОТЫ
1.Найти уравнение плоскости, проходящей через прямую
перпендикулярно плоскости: 3х – 5 у + 5 z + 3 = 0.
Решение. Искомая плоскость a будет проходить через данную прямую, а следовательно через точку прямой М0 (2; – 3; – 1). Направляющий вектор 




Разложим определитель по первой строке


a: 
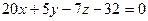
Ответ: 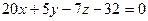
2.Даны плоскости, заданные в О 
a: 2х – 3у + 3 = 0, b: х – у + z +2 = 0.
Найти уравнение плоскости, проходящей через линию пересечения данных плоскостей и перпендикулярную плоскости b.
Решение. Найдем две общие точки данных плоскостей. Для этого решим систему уравнений:
Пусть у = 0, тогда система примет вид
Отсюда получим, что х = 

Решением системы будет тройка чисел 


Отсюда получим, что х = 0, z = 



Из уравнения плоскости b находим ее нормальный вектор 
Для составления уравнения искомой плоскости обратим внимание на то, что точки М1 и М2 принадлежат ей, а вектор 

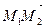








3.Найти каноническое уравнение прямой, проходящей через точку А(6; 2; 3) перпендикулярно плоскости, проходящей через точки В (1; 4; 4), С (0; 2; 4), D (1; 3; 3).
Решение. Найдем уравнение плоскости (BCD) по трем точкам B, C, D


Разложив определитель по первой строке, получим уравнение плоскости (BCD):

Нормальный вектор 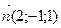
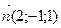


Ответ: 
4. Даны прямые, заданные в О 
ℓ1: 

Найти уравнение плоскости, проходящей через первую прямую параллельно второй прямой.
Решение. Согласно условию задачи точка М0 (– 1; – 1; 4), принадлежащая первой прямой, лежит в искомой плоскости. Кроме этого имеем два вектора: 

a: 
Раскрываем определитель по первой строке:
= – 3(х + 1) + 6(у +1) – 12(z – 4) = – 3х + 6у – 12z +51.
Следовательно, – 3х + 6у – 12z +51 = 0 и получаем уравнение плоскости a: х –2у + 4z – 17 = 0.
5. Вычислить расстояние от точки P (-1; 1; -2) до плоскости, проходящей через точки, заданные в О 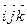
Решение. Найдем уравнение плоскости (АВС) по трем заданным точкам:

Разложив определитель по первой строке, получим:

Следовательно, 
Воспользуемся известной формулой для вычисления расстояния от точки до плоскости

Ответ: 
Тест
Отметьте номер правильного ответа в бланке ответов
| Задания | Варианты ответов | |
| А1 | Написать уравнение прямой, проходящей через две заданные точки М1(1; – 2; 1) и М2(3; 1; – 1) | 1)  2) 2)  3) 3)  4) 4)  5) 5)  =0 =0 |
| A2 | Найти расстояние от точки М0 (–1; 2) до прямой ℓ:  | 1)  2) 2)  3) 2 4) 5 5) 3) 2 4) 5 5)  |
| A3 | Найти расстояние между прямыми ℓ1: 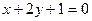 и ℓ2: и ℓ2:  | 1) 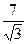 2) 5 3) 2) 5 3)  4) 4)  5) 6 5) 6 |
| А4 | Найти косинус угла между прямыми ℓ1 и ℓ2, если ℓ1 :  и ℓ2: и ℓ2:  | 1)  2) 2)  3) 3)  4) 4)  5) 0 5) 0 |
| А5 | Найти уравнение касательной к окружности  в точке в точке  | 1)  2) 2)  3) 3)  4) 4)  5) 5)  |
| А6 | Две стороны квадрата лежат на прямых ℓ1 :  и ℓ2: и ℓ2:  . Вычислить его площадь . Вычислить его площадь | 1) 64 2) 81 3) 16 4) 49 5) 25 |
| А7 | В О  заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение прямой (ВС). заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение прямой (ВС). | 1)  2) х + у – 1=0 3) у = х +1 4) 2) х + у – 1=0 3) у = х +1 4)  5) х – у + 1=0 5) х – у + 1=0 |
| А8 | В О  заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение медианы (АМ) треугольника АВС. заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение медианы (АМ) треугольника АВС. | 1)  2)х– у+1=0 3)х+3у –3=0 4) 3х+у – 3=0, 5) 2)х– у+1=0 3)х+3у –3=0 4) 3х+у – 3=0, 5)  |
| А9 | В О  заданы точки: А(1; 1), В(0; 2), С(2; 4) Найти общее уравнение биссектрисы угла ÐАВС. заданы точки: А(1; 1), В(0; 2), С(2; 4) Найти общее уравнение биссектрисы угла ÐАВС. | 1) х – у = 0, 2) 2х+3у – 1 =0, 3) х = 2, 4) у – 2 = 0, 5) у = 2х. |
| А10 | В О  заданы точки: А(1; 1),В(0; 2), С(2; 4). Вычислить расстояние от точки А до биссектрисы угла В в треугольнике АВС. заданы точки: А(1; 1),В(0; 2), С(2; 4). Вычислить расстояние от точки А до биссектрисы угла В в треугольнике АВС. | 1) 1, 2) -2, 3) 4, 4) 0, 5) 2. |
| А11 | В О  заданы точки:А(1; 1), В(0; 2), С(2; 4). Вычислить площадь треугольника АВВ1 , где ВВ1 — биссектриса угла В в треугольнике АВС. заданы точки:А(1; 1), В(0; 2), С(2; 4). Вычислить площадь треугольника АВВ1 , где ВВ1 — биссектриса угла В в треугольнике АВС. | 1) 2, 2) 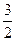 , 3) , 3)  , 4) -1, 5) 3 , 4) -1, 5) 3 |
| А12 | В О  заданы плоскости a:х-у+z = -3, b: 2x-3z+4=0 найти уравнение плоскости, проходящей через линию пересечения данных плоскостей и ^ a. заданы плоскости a:х-у+z = -3, b: 2x-3z+4=0 найти уравнение плоскости, проходящей через линию пересечения данных плоскостей и ^ a. | 1)х – у — 8z=19; 2)21x — 3y — 24z+19=0; 3)x — 3y+5z — 21=0; 4) x+3y — 5z — 21=0; 5) 21x — 3y+24z+19=0 |
| A13 | Уравнение прямой имеет вид, если она проходит через точку В(4,2,-3) и перпендикулярна плоскости ACD, где A(1,-1,1), C(0,2,4), D(1,3,3), (O 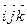 ). ). | 1)21x-3y+24z+19=0;2)  3) 3)  ; 4)х – у – z +3=0; 5) ; 4)х – у – z +3=0; 5)  |
| А14 | Уравнение плоскости ACD имеет вид, где A(1,-1,1),C(0,2,4), D(1,3,3), (O 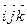 ). ). | 1) 3х – у + 2z – 6 =0, 2) 3х + у + 2z + 6 =0, 3) у + 2z – 6 =0, 4) 3х + 2z – 6 =0, 5) 3х – у -2z – 6 =0 |
| A15 | Найти расстояние от точки B(4,2,-3) до плоскости ACD, где A(1,-1,1),C(0,2,4), D(1,3,3), (O 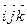 ). ). | 1) 2, 2)  , 3) 3, 4) , 3) 3, 4)  , 5) , 5)  |
| А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | А11 | А12 | А13 | А14 | А15 |
Список литературы
1. А.Д. Александров, Н.Ю. Нецветаев. Геометрия. — М.: Наука, 1990.
2. Л.С. Атанасян, В.Т. Базылев. Геометрия. Ч. 1. — М.: Просвещение, 1986.
3. В.Т. Базылев, К.И. Дуничев и др. Геометрия. — Ч. 1. — М.: Просвещение, 1974.
4. В.Т. Базылев, К.И. Дуничев и др. Под ред. В.Т. Базылева. Сборник задач по геометрии. — М.: Просвещение, 1980.
5. Беклемишева Л.А. и др. Сборник задач по аналитической геометрии: Уч.пособие. –М. 2003.
6. Бортаковский А.С., Пантелеев А.В. Аналитическая геометрия в примерах и задачах: Учебное пособие. –М.: Высшая школа, 2005.
7. А.Л. Вернер, Б.Е. Кантор, С.А. Франгулов. Геометрия, ч.1.- С. Петербург, 1997.
8. Л.С. Атанасян, В.А. Атанасян. Сборник задач по геометрии. Ч. 1. — М.: Просвещение, 1973.
9. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. –М., 2004. –464 с.
10. Ефимов Н.В. Высшая геометрия: Учебник для вузов. –.М.: Физматлит, 2003. –584 с.
11. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.1. –Новосибирск: Сиб.унив.изд-во, 2002. –271 с.
12. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.2. –Новосибирск: Сиб.унив.изд-во, 2003. –267 с.
13. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. –М.: МГУ, 1980. –320 с.
14. Д.В. Клетеник. Сборник задач по аналитической геометрии. — М.: Наука, 1964.
15. А.В. Погорелов. Геометрия. — М.: Наука, 1984.
16. О.Н. Цубербиллер. Сборник задач по аналитической геометрии. — М.: Наука, 1966.
Виктор Анатольевич Долженков
Елена Георгиевна Соловьева
Игорь Викторович Горчинский
Лицензия ИД № 06248 от 12.11.2001 г.
Подписано в печать Формат 60х84/16. Печать офсетная.
💥 Видео
§30 Уравнения кривых второго порядка в полярных координатахСкачать

Полярная система координатСкачать

Видеоурок "Полярная система координат"Скачать

Скорость и ускорение точки в полярных координатахСкачать

Оператор Лапласа в полярных координатахСкачать

Полярные координаты. Полярное уравнение эллипса.Скачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Овчинников А. В. - Аналитическая геометрия - Уравнения линий второго порядка в полярных координатахСкачать

§12 Полярное уравнение прямойСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Глаза гипножабы и площадь фигур в полярной системе координатСкачать

§52 Полярная система координатСкачать

Полярная система координат на плоскостиСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Полярная система координат.Скачать

Двойной интеграл в полярных координатахСкачать

Площадь фигуры, заданной в полярной системе координатСкачать