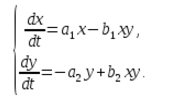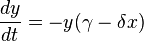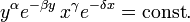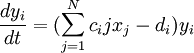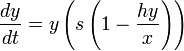Что такое модель Лотки-Вольтерры и как она помогает биологам
Могут ли сложные математические инструменты применяться в биологии? Могут, если биологи изучают сложные динамические системы, например взаимодействие разных видов животных в естественной среде. Американец Альфред Лотка и итальянец Вито Вольтерра разработали модель, позволяющую описывать, как будет меняться поголовье хищников и их травоядных жертв в зависимости от множества привходящих условий. Это наш второй материал о самых интересных дифференциальных уравнениях (с первым можно ознакомиться здесь). Если вы читаете нас с телефона, переключайте страницу на десктопную версию, так вы сможете увидеть интерактивный график целиком.
Изначально Альфред Лотка вообще не планировал создавать никаких математических моделей. Он собирался разработать новую предметную область — «физическую биологию» — и поэтому начиная с 1902 года стал публиковать небольшие статьи, посвященные этой теме.
Параллельно с этим его все более интересовало применение математических методов в биологии. Идеи Лотки, однако, не получили широкого распространения — в то время американский ученый не имел широких связей в научной среде и работал в одиночестве.
Ситуация изменилась в 1920 году, когда статьи Лотки привлекли внимание биолога и статистика Раймонда Пирла, который нашел в них близкие для себя идеи: Пирл интересовался ростом популяции в пределах одного вида.
Лотка написал еще одну статью, и Пирл помог продвинуть ее в Proceedings of the National Academy of Sciences (ведущий американский журнал для публикации оригинальных научных исследований в различных областях). В этой статье Лотка в качестве примера описал взаимодействие растения и травоядного и пришел к неожиданному для него результату: их взаимодействие приведет к бесконечному циклическому колебанию в двух популяциях!
Позже Лотка расширил это наблюдение до общего случая взаимодействия типа «хищник-жертва».
Итальянский ученый Вито Вольтерра, как и Альфред Лотка, пришел к этой модели со стороны точных наук. Он с раннего детства питал тягу к математике и занимался ею всю свою жизнь, и уже в 1900-е годы заинтересовался возможностью использовать математику в биологии и общественных науках.
После окончания Первой мировой войны Вольтерра погрузился в биологию и, сам того не зная, пришел к выводам, схожим с выводами Альфреда Лотки, сделанными ранее. Однако именно работы Вольтерры привлекли внимание математического сообщества.
В итоге Вольтерра, чья статья вышла в 1926 году, признал приоритет Лотки. Но чтобы его собственные работы не выглядели бессмысленными, Вольтерра отметил, что рассмотрел ситуацию в более общем случае: вывел уравнения, которые описывают взаимодействие более чем двух видов и учитывают их контакт в прошлом.
Модель Лотки-Вольтерры
Система Лотки-Вольтерры является первоначальной и простейшей системой (усложненные системы будут рассмотрены ниже) для описания модели «хищник-жертва», то есть популяции хищников и популяции жертв, взаимодействующих в какой-то среде: жертвы едят растительность, хищники — жертв:
Видео:Абдулов Тимур. Этапы построения математической модели. Реализация математической моделиСкачать

Модель «хищник-жертва»
Вы будете перенаправлены на Автор24
Часто представители одного вида (популяции) питаются представителями другого вида.
Модель Лотки – Вольтерры – модель взаимного существования двух популяций типа «хищник – жертва».
Названа в честь авторов модели – Лотка и Вольтерра, которые представили уравнения модели независимо друг от друга. Довольно распространенным является неправильное название – модель Лотки – Вольтерра.
Впервые модель «хищник – жертва» была получена А. Лоткой в 1925 году, который использовал ее для описания динамики взаимодействующих биологических популяций. В 1926 году независимо от Лотки аналогичные (к тому же более сложные) модели были разработаны итальянским математиком В. Вольтерра, глубокие исследования которого в области экологических проблем заложили фундамент математической теории биологических сообществ или т. н. математической экологии.
В математической форме предложенная система уравнений имеет вид:
где x – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, которые отражают взаимодействия между популяциями.
Уравнения используются для моделирования системы «хищник – жертва», «паразит – хозяин», конкуренции и других видов взаимодействия между двумя видами.
Видео:Мат моделирование. Лаба 5. Модель Лотки-Вольтерры. ПрезентацияСкачать

Постановка задачи
Рассмотрим закрытое пространство, в котором существуют две популяции – травоядные («жертвы») и хищники. Считается, что животных не ввозят и не вывозят и что еды для травоядных животных достаточно. Тогда уравнение изменения числа жертв (только жертв) примет вид:
Готовые работы на аналогичную тему
где $α$ – коэффициент рождаемости жертв,
$x$– размер популяции жертв,
$frac
Когда хищники не охотятся, они могут вымирать, значит, уравнение для количества хищников (только хищников) примет вид:
, где $γ$ – коэффициент убыли хищников,
$y$ – размер популяции хищников,
$frac
При встрече хищников и жертв (частота встреч прямо пропорциональна произведению ) хищники уничтожают жертв с коэффициентом , сытые хищники могут воспроизводить потомство с коэффициентом . Таким образом, система уравнений модели примет вид:
Видео:График колебания численности хищник – жертва. БиологияСкачать

Решение задачи
Построим математическую модель совместного существования двух биологических популяций типа «хищник – жертва».
Пусть две биологические популяции совместно обитают в изолированной среде. Среда является стационарной и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов – жертвы. Другой вид – хищник – также обитает в стационарных условиях, но питается только жертвами. В роли хищников могут выступать коты, волки, щуки, лисы, а в роли жертв – куры, зайцы, караси, мыши соответственно.
Для определенности рассмотрим в роли хищников – котов, а в роли жертв – кур.
Итак, куры и коты живут в некотором изолированном пространстве – хозяйственном дворе. Среда предоставляет курам питание в неограниченном количестве, а коты питаются только курами. Обозначим через
$х$ – количество кур,
$у$ – количество котов.
Со временем количество кур и котов меняется, но будем считать $х$ и $у$ непрерывными функциями от времени t. Назовем пару чисел $х, у)$ состоянием модели.
Найдем каким образом изменяется состояние модели $(х, у).$
Рассмотрим $frac
Если котов нет, то количество кур возрастает и тем быстрее, чем больше кур. Будем считать зависимость линейной:
$a_1$ – коэффициент, который зависит только от условий жизни кур, их естественной смертности и рождаемости.
$frac
Если кур нет, то количество котов уменьшается (у них нет пищи) и они вымирают. Будем считать зависимость линейной:
В экосистеме скорость изменения количества каждого вида также будем считать пропорциональным его количеству, но только с коэффициентом, зависящим от количества особей другого вида. Так, для кур этот коэффициент уменьшается с увеличением количества котов, а для котов возрастает с увеличением количества кур. Будем считать зависимость также линейной. Тогда получим систему дифференциальных уравнений:
Данная система уравнений называется моделью Вольтерра-Лотки.
a1, a2, b1, b2 – числовые коэффициенты, которые называют параметрами модели.
Как видно, характер изменения состояния модели (x, y) определяется значениями параметров. Изменяя данные параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.
С помощью программы MATLAB система уравнений Лотки-Вольтерра решается следующим образом:
На рис. 1 представлено решение системы. В зависимости от начальных условий решения разные, чему отвечают разные цвета траекторий.
На рис. 2 представлены те же решения, но с учетом оси времени t (т.е. наблюдается зависимость от времени).
Видео:2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

Уравнения Лотки-Вольтерры
Уравнения Лотки — Вольтерры или уравнения хищник — жертва — система двух обыкновенных дифференциальных уравнений первого порядка, описывающей кинетику численности популяции с одним типом хищников и одним типом жертв. Характерной особенностью ривннянь является то, что их решением является автоколебания. Уравнение предложили независимо Альфред Джеймс Лотка и Вито Вольтерра, в 1925 и 1926 годах, соответственно.
Уравнения имеют вид
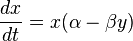
где x — количество жертв, например, зайцев, y — количество хищников, например, волков, — определенные параметры.
В уравнение входят следующие процессы: размножение жертв и их гибель в результате поедания хищниками, размножения и вымирания хищников. Считается, что размножение хищников пропорционально количеству пищи, то есть, количества потенциальных жертв в популяции.
Видео:Early Predator/Prey model after several training iterations.Скачать

Стационарные точки
Система уравнение имеет два стационарные точки:
- x = 0, y = 0 — эта точка соответствует отсутствию в популяции как жертв, так и хищников.
Анализ устойчивости стационарных точек показывает, что первая из них (нулевая) является седловой, а вторая — фокусом. Показатель Ляпунова для фокуса чисто мысленный, поэтому с линейного анализа сделать вывод об устойчивости или неустойчивости фокуса невозможно. Однако для уравнений Лотка-Вольтерра существует интеграл движения, показывает, что фазовые траектории — замкнутые кривые, внутри которых находится фокус.
Видео:Раздел 5. Биология. Компьютерное моделирование высокой детализации.Скачать

Интеграл движения
Для решения уравнения Лотки-Вольтерра существует интеграл движения
Типичные фазовые траектории показаны на рисунке справа. При значительном размножении жертв создаются условия для размножения хищников благодаря доступности пищи. Но размножения хищников приводит к уменьшению числа жертв. Когда число жертв сильно падает, хищники тоже погибают из-за недостатка пищи. Только тогда, когда количество хищников достигает минимума, популяция жертв снова начинает расти.
Существование интеграла движения приводит к тому, что величины популяций определяются начальными условиями. В этой задач не предельного цикла, который был бы аттракторов для фазовых траекторий. Циклы в задачи хищник-жертва имеют равнодушную устойчивость.
Видео:Модель "Хищник-жертва" в экономикеСкачать

Обобщенная модель Лотки-Вольтерры
Модель Лотки-Вольтерра может быть обобщена для многих популяций (N). Для них мы имеем такие уравнения:
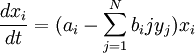
где параметры имеют такой же смысл как в модели с двумя видами организмов.
Видео:Рубин А. Б. - Биофизика I - Базовая модель «Хищник-жертва»Скачать
Реалистичная модель «хищник-жертва»
Главный недостаток модели Лотки-Вольтерры заключается в том, что при нулевой численности хищников популяция жертв неограниченно растет. Таким образом, в реалистичных моделях, описывающих это явление должно быть пропускная способность K — максимальное число лиц которой может достигать размер популяции. Уравнение учитывает этот фактор приведены ниже:
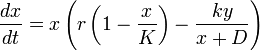
— Находятся в постоянной зависимости от модели.
📹 Видео
Уравнения Вольтерра - 1Скачать

Математика I. Лекция 3. Дифференциальные уравнения. Лектор Н.А. ХохловСкачать

Динамика биологических популяций 2Скачать

Математическое моделирование. Лабораторная работа № 5 "Модель хищник-жертва"Скачать

Информатика 11 класс (Урок№10 - Математические модели. Стохастические модели.)Скачать

Тихонов Н. А. - Основы математического моделирования - Типы математических моделей (Лекция 1)Скачать

ПР ПопуляцияСкачать

Лабораторная работа №5. Модель хищник-жертва (презентация)Скачать

Почему деревья не растут до небаСкачать

Модели взаимодействия видовСкачать

ИМРС 1.3 Аналитическое и имитационное моделирование массы-пружины-демпфераСкачать

Математическое моделирование - Лекция 1 (09.02.07)Скачать