Уравнение логических функций для схемы (8 видео)

Логические схемы и таблицы истинности

Логические схемы создаются для реализации в цифровых устройствах булевых функций (функций алгебры логики).

В цифровой схемотехнике цифровой сигнал — это сигнал, который может принимать два значения, рассматриваемые как логическая «1» и логический «0».

Логические схемы могут содержать до 100 миллионов входов и такие гигантские схемы существуют. Представьте себе, что булева функция (уравнение) такой схемы была потеряна. Как восстановить её с наименьшими потерями времени и без ошибок? Наиболее продуктивный способ — разбить схему на ярусы. При таком способе записывается выходная функция каждого элемента в предыдущем ярусе и подставляется на соответствующий вход на следующем ярусе. Этот способ анализа логических схем со всеми нюансами мы сегодня и рассмотрим.

Логические схемы реализуются на логических элементах: «НЕ», «И», «ИЛИ», «И-НЕ», «ИЛИ-НЕ», «Исключающее ИЛИ» и «Эквивалентность». Первые три логических элемента позволяют реализовать любую, сколь угодно сложную логическую функцию в булевом базисе. Мы будем решать задачи на логические схемы, реализованные именно в булевом базисе.

Для обозначения логических элементов используется несколько стандартов. Наиболее распространёнными являются американский (ANSI), европейский (DIN), международный (IEC) и российский (ГОСТ). На рисунке ниже приведены обозначения логических элементов в этих стандартах (для увеличения можно нажать на рисунок левой кнопкой мыши).

На этом уроке будем решать задачи на логические схемы, на которых логические элементы обозначены в стандарте ГОСТ.

Задачи на логические схемы бывают двух видов: задача синтеза логических схемы и задачи анализа логических схем. Мы начнём с задачи второго типа, так как в таком порядке удаётся быстрее научиться читать логические схемы.

Чаще всего в связи с построением логических схем рассматриваются функции алгебры логики:

трёх переменных (будут рассмотрены в задачах анализа и в одной задаче синтеза);
четырёх переменных (в задачах синтеза, то есть в двух последних параграфах).

Рассмотрим построение (синтез) логических схем

в булевом базисе «И», «ИЛИ», «НЕ» (в предпоследнем параграфе);
в также распространённых базисах «И-НЕ» и «ИЛИ-НЕ» (в последнем параграфе).

На основе логических выражений и функций строятся логические схемы. Бывает, что изначально составленная функция является излишне сложной, из-за чего её схемная или программная реализация оказывается избыточной. Способам и приёмам минимизации логических функций посвящены отдельные материалы сайта — минимизация логических функций: общие сведения и минимизация логических функций: метод непосредственных преобразований.

Содержание

Задача анализа логических схем
Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение
Продолжаем искать булеву функцию логической схемы вместе
Задача синтеза логических схем в булевом базисе
Задача синтеза логических схем в базисах «И-НЕ» и «ИЛИ-НЕ»
Построение логических схем
Схемотехника. Минимизация логических функций
Зачем это нужно?
Минимизация логических функций при помощи карт Карно
📸 Видео

Видео:Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

Задача анализа логических схем

Задача анализа заключается в определении функции f , реализуемой заданной логической схемой. При решении такой задачи удобно придерживаться следующей последовательности действий.

Логическая схема разбивается на ярусы. Ярусам присваиваются последовательные номера.
Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра — номер яруса, а остальные цифры — порядковый номер элемента в ярусе.
Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.

Пример 1. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы, что уже показано на рисунке. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z :

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

Видео:Построение логических схемСкачать

Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение

Пример 2. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Пример 3. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Видео:Построение логических функций и схемСкачать

Продолжаем искать булеву функцию логической схемы вместе

Пример 4. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z :

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	0	1	1
1	1	0	0	1	1
1	0	1	1	0	1
1	0	0	0	0	0
0	1	1	0	1	1
0	1	0	0	1	1
0	0	1	0	1	1
0	0	0	0	1	1

Пример 5. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Структура данной логической схемы, в отличие от предыдущих примеров, имеет 5 ярусов, а не 4. Но одна входная переменная — самая нижняя — пробегает все ярусы и напрямую входит в логический элемент в первом ярусе. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z :

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	1	1	1
1	1	0	1	1	1
1	0	1	1	0	1
1	0	0	1	0	1
0	1	1	1	1	1
0	1	0	1	1	1
0	0	1	1	0	1
0	0	0	1	0	1

Видео:Построение схем по логическим выражениямСкачать

Задача синтеза логических схем в булевом базисе

Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы.

Каждой дизъюнкции (логической сумме) соответствует элемент «ИЛИ», число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент «И», число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент «НЕ».

Часто разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схемы. В этом случае дана только таблица истинности логической схемы. Мы разберём именно такой пример, то есть, решим задачу, полностью обратную рассмотренной выше задаче анализа логических схем.

Пример 6. Построить логическую схему, реализующую функцию с данной таблицей истинности:

x	y	f
1	1	0
1	0	0
0	1	1
0	0	0

Решение. Разбираем таблицу истинности для логической схемы. Определяем функцию, которая получится на выходе схемы и промежуточные функции, которые на входе принимают аргументы x и y . В первой строке результатом реализации выходной функции при том, что значения входных переменных равны единицам, должен быть логический «0», во второй строке — при разных значениях входных переменных на выходе тоже должен быть логический «0». Поэтому нужно, чтобы выходная функция была конъюнкцией (логическим произведением).

Теперь подбираем промежуточные функции. Получаем следующую таблицу для промежуточных функций и выходной функции — конъюнкции промежуточных функций:


0	0	0
0	1	0
1	1	1
0	1	0

Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Из выражения видно, что понадобятся 3 схемы «НЕ», две двухвходовых схемы «И» и одна двухвходовая схема «ИЛИ». В соответствии с выходной функцией получаем следующую логическую схему:

А теперь очередь дошла до функций алгебры логики четырёх переменных. Сначала выполним синтез логической схемы в булевом базисе.

Пример 7. Построить в булевом базисе логическую схему, реализующую функцию алгебры логики

Решение. Для построения логической схемы потребуются 4 схемы «НЕ», одна трёхвходовая схема «И», 2 двухвходовые схемы «И» и одна трёхвходовая схема «ИЛИ». В соответствии с этим получаем следующую логическую схему:

Видео:Построение таблиц истинностиСкачать

Задача синтеза логических схем в базисах «И-НЕ» и «ИЛИ-НЕ»

Часто для сокращения числа микросхем используют элементы «И-НЕ» или/и «ИЛИ-НЕ». Рассмтрим примеры, как построить схему, реализующую ту же функцию, что в предыдущем примере, но, сначала в базисе «И-НЕ», а затем в базисе «ИЛИ-НЕ».

Пример 8. Построить в базисе «И-НЕ» логическую схему, реализующую функцию алгебры логики .

Решение. Логическая функция должна быть приведена к виду, содержащему только операции логического умножения (конъюнкции) и инвертирования (отрицания). Это делается при помощи двойного инвертирования исходного выражения функции и применения закона де Моргана:

Для построения логической схемы потребуются 8 схем «И-НЕ». Получаем следующую логическую схему:

Пример 9. Построить в базисе «ИЛИ-НЕ» логическую схему, реализующую функцию алгебры логики .

Видео:Сколько решений имеет лог. уравнение (!(A *B) + C) IMP (!A * !B + D) = 1. Информатика, ЕГЭ, логикаСкачать

Построение логических схем

Цели урока:

Образовательные:

закрепить у учащихся представление об устройствах элементной базы компьютера;
закрепить навыки построения логических схем.

Развивающие:

формировать развитие алгоритмического мышления;
развить конструкторские умения;
продолжать способствовать развитию ИКТ — компетентности;

Воспитательные:

продолжить формирование познавательного интереса к предмету информатика;
воспитывать личностные качества:
активность,
самостоятельность,
аккуратность в работе;

Требования к знаниям и умениям:

Учащиеся должны знать:

основные базовые элементы логических схем;
правила составления логических схем.

Учащиеся должны уметь:

составлять логические схемы.

Тип урока: урок закрепления изученного материала

Вид урока: комбинированный

Методы организации учебной деятельности:

фронтальная;
индивидуальная;

Программно-дидактическое обеспечение:

ПК, SMART Board, карточки с индивидуальным домашним заданием.

Урок разработан с помощью программы Macromedia Flash.

Ход урока

I. Постановка целей урока.

Сегодня мы продолжаем изучение темы «Построение логических схем».

Приготовьте раздаточный материал «Логические основы ЭВМ. Построение логических схем» Приложение 1

Вопрос учителя. Назовите основные логические элементы. Какой логический элемент соответствует логической операции И, ИЛИ, НЕ?

Ответ учащихся. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Основные логические элементы конъюнктор (соответствует логическому умножению), дизъюнктор (соответствует логическому сложению), инвертор (соответствует логическому отрицанию).

Вопрос учителя. По каким правилам логические элементы преобразуют входные сигналы. Рассмотрим элемент И. В каком случае на выходе будет ток (сигнал равный 1).

Ответ учащихся. На первом входе есть ток (1, истина), на втором есть (1, истина), на выходе ток идет (1, истина).

Вопрос учителя. На первом входе есть ток, на втором нет, однако на выходе ток идет. На входах тока нет и на выходе нет. Какую логическую операцию реализует данный элемент?

Ответ учащихся. Элемент ИЛИ — дизъюнктор.

Вопрос учителя. Рассмотрим логический элемент НЕ. В каком случае на выходе не будет тока (сигнал равный 0)?

Ответ учащихся. На входе есть ток, сигнал равен 1.

Вопрос учителя. В чем отличие логической схемы от логического элемента?

Ответ учащихся. Логические схемы состоят из логических элементов, осуществляющих логические операции.

Проанализируем схему и определим сигнал на выходе.

II. Закрепление изученного материала.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.

Дома вам необходимо было построить логические схемы, соответствующие логическим выражениям.

Вопрос учителя. Каков алгоритм построение логических схем?

Ответ учащихся. Алгоритм построение логических схем:

Определить число логических переменных.

Определить количество базовых логических операций и их порядок.

Изобразить для каждой логической операции соответствующий ей элемент (вентиль).

Соединить вентили в порядке выполнения логических операций.

Проверка домашнего задания Приложение 1. Домашнее задание. Часть 1

Построить логическую схему для логического выражения: .

Две переменные — А и В.
Две логические операции: &,
Строим схему.

Построить логическую схему для логического выражения:

Вычислить значение данного выражения для А=1, В=0.

III. Пропедевтика (законы логики)

Выполним задачу обратную данной. Составим логическое выражение по заданной логической схеме:

Данное логическое выражение можно упростить.

Операция И — логическое умножение, ИЛИ — сложение. Запишем выражение, заменяя знаки & и U на * и + соответственно.

F= (A*B+B*С) Упростим F= (B*(А+С)), затем запишем и тогда логическая схема примет вид:

Вывод: Логические схемы, содержащие минимальное количество элементов, обеспечивают большую скорость работы и увеличивают надёжность устройства.

Алгебра логики дала конструкторам мощное средство разработки, анализа и совершенствования логических схем. Проще, и быстрее изучать свойства и доказывать правильность работы схемы с помощью выражающей её формулы, чем создавать реальное техническое устройство.

Таким образом, цель нашего следующего урока — изучить законы алгебры логики.

IV. Домашнее задание. Часть 2

V. Практическая работа.

Программа — тренажер «Построение логических схем»

Видео:Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6Скачать

Схемотехника. Минимизация логических функций

Зачем это нужно?

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.

К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.

В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.

Минимизация логических функций при помощи карт Карно

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Возможность поглощения следует из очевидных равенств

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

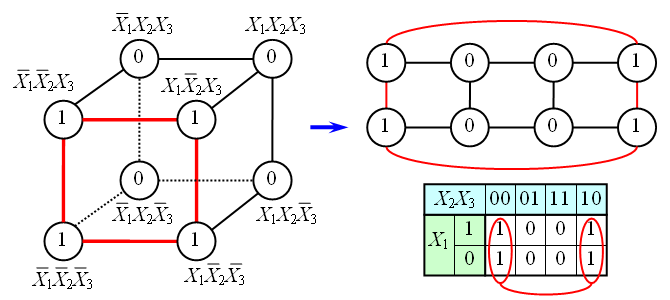
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

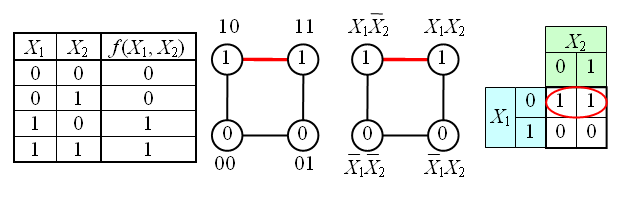
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

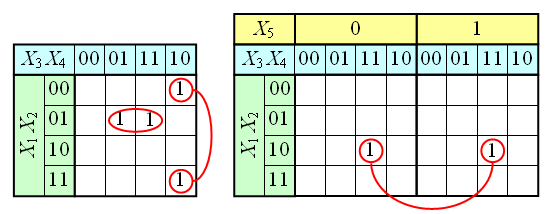
Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n (n целое число = 0…) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
Область должна быть как можно больше, а кол-во областей как можно меньше;
Области могут пересекаться;
Возможно несколько вариантов накрытия.

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):