1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .
2. Нарисуйте кривую, задаваемую уравнением r = cos φ .
3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

4. Докажите, что уравнение

задает эллипс, если 0 

5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?
6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?
7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = 
8. Нарисуйте спираль Галилея , которая задается уравнением r = a 
9. Нарисуйте кривую, задаваемую уравнением r = | 
10. Нарисуйте кривую, задаваемую уравнением r = 
11. Нарисуйте кривую, задаваемую уравнением r = 
12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.
1. Березин В. Кардиоида //Квант. – 1977. № 12.
2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.
3. Берман Г.Н. Циклоида. – М.: Наука, 1975.
4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.
5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.
6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.
7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.
8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.
9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.
10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.
Видео:Полярная система координатСкачать

Уравнение логарифмическая спираль в полярной системе координат
Логарифмическая спираль – плоская трансцендентная кривая. Ее уравнение в полярных координатах имеет вид
ρ = ае kφ , (*)
где k = ctg a (см. рис.).
При a = p /2 параметр k = 0 и кривая «вырождается» в окружность. Она пересекает все свои радиус-векторы под одним и тем же углом a ; по этой причине ее называют иногда «равноугольной».
Полюс О системы полярных координат (в которых уравнение кривой имеет вид (*)) – асимптотическая точка кривой (кривая к ней неограниченно приближается при φ → –∞).
Длина L дуги кривой между ее точками (ρ1; φ1) и (ρ2; φ2) вычисляется по формуле 
а длину L0 дуги от точки (ρ; φ) до асимптотической точки – полюса – можно вычислить так:
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Исследовательская работа «Логарифмическая ВСЕЛЕННАЯ»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Без знания математики нельзя понять ни основ современной техники, ни того, как
ученые изучают природные и социальные явления» ( Колмогоров. А.Н.)
«Изменённая, возрождаюсь прежней». Якоб Бернулли
Исследовательская работа «Логарифмическая ВСЕЛЕННАЯ» по математике,
Кузнецова Раиса Михайловна, учитель.
Математик – это сложно. Как часто мы слышим эти слова. Само это слово внушает страх многим. Давайте приоткроем дверь в увлекательную страну Математика, заглянем в одну из ее непостижимых тайн.
«Какая наука может быть более благородна, более восхитительна,
более полезна для человечества, чем математика»
Следуя совету А.М.Горького, всякий, изучающий математику, должен не только вобрать в себя готовые положения этой науки, но и возможно глубже познать те пути, по которым шла человеческая мысль, создавая эти положения.
Поэтому я попытаюсь выяснить, где можно «встретить» логарифмическую спираль в жизни, в природе, в космосе, в архитектуре, в живописи, и почему она встречается так часто.
Дело в том, что на протяжении 16 века быстро возрастало количество приближенных вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономам грозила реальная опасность утонуть в невыполненных расчетах.
Тогда математики для облегчения вычислений придумали логарифмы. И три столетия с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные шотландским математиком Джоном Непером (1550–1617), они верой и правдой служили астрономам и инженерам, геодезистам и морякам, сокращая время на вычисления и тем самым, как сказал знаменитый французский учёный Лаплас (1749 – 1827), удлиняя жизнь вычислителям . «Канон о логарифмах» Джона Непера начинался так: «Осознав, что в математике нет ничего более скучного и утомительного, чем умножение, деление, извлечение квадратных и кубических корней, и что названные операции являются бесполезной тратой времени и неиссякаемым источником неуловимых ошибок, я решил найти простое и надежное средство, чтобы избавиться от них»
Проблема: общеизвестно, что в школьном курсе алгебры изучаются логарифмы и логарифмические функции. А логарифмическая спираль, которая в природе встречается повсеместно, не рассматривается.
. Цели: увидеть знакомое в незнакомом; расширить представление о логарифмической спирали и попытаться понять, почему она встречается так часто.
Гипотеза: Логарифмическая спираль — интересный феномен, который связывает не связанные между собой явления, это математический язык, на котором говорит с нами природа.
Актуальность работы : не вызывает сомнения, так как с давних времен затрагивала умы математиков, географов и биологов. В практической жизни и природе логарифмическая спираль встречается часто, но полностью не изучена, поэтому вызывает интерес у исследователей.
- Выдвижение гипотезы
- Сбор материала и работа над литературой по теме
- Исследование проявления логарифмической спирали в различных явлениях и практической жизни:
в) в стихийных явлениях;
е) в архитектуре.
4. Написание работы
5. Подготовка презентации
1.Подготовительный: Подбор научной литературы. Сбор информации.
2.Основной: Обработка информации.
3. Заключительный: Создание презентации.
2. Исторические сведения: а) история возникновения; в) историческая хронология.
3. Основная часть:
a) Логарифмическая спираль в математике
b) Удивительное рядом
c) Логарифмическая спираль в природе
d) Логарифмическая спираль в стихийных явлениях
e) Логарифмическая спираль в космосе
f) Логарифмическая спираль в живописи
g) Логарифмическая спираль в архитектуре
Начало исследования этой спирали связано, скорее всего, с навигацией. На протяжении XVI и XVII веков тысячи судов бороздили океаны. Мореплаватели знали, что на поверхности Земли кратчайшее расстояние между двумя точками дает дуга окружности. Но чтобы двигаться по такой дуге следует непрерывно менять направление движения. Поэтому этот оптимальный курс заменяли другим, таким, чтобы угол, под которым корабль пересекал все меридианы, был постоянным. Этот курс оставался постоянным. Траектории такого вида образуют на земной поверхности кривые, которые называются локсодромами. Однако моряки не работали на сфере, их карты были плоскими, они представляли собой проекции сферы. Ну а проекция сферы на плоскость преобразует локсодрому на ней в… логарифмическую (или равноугольную) спираль.
Первым, кто описал ее как механическую кривую, был Декарт в 1638 г. Он показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов. Отсюда и название: логарифмическая спираль.
Расстояние между витками растет с увеличением угла, т. е. радиус-вектор увеличивается с увеличением угла поворота. Так что третье название этой кривой – геометрическая спираль.
Отцом этой спирали, по всей справедливости, является швейцарский математик Якоб Бернулли, который ее полностью изучил и, которого она настолько заворожила, что он назвал спираль изумительной ( spira mirabilis ). Он даже завещал высечь её на своем надгробии вместе с латинским изречением « Eadem mutata resurgo » – «Изменённая, возрождаюсь прежней». (Или “Измененная, я вновь воскресаю’’).
Каменотес не был хорошим математиком, и он вырезал на камне практически идеальную архимедову спираль.
Логарифмическая спираль была впервые описана Декартом (1638 г., опубликовано в 1657 г). Декарт искал кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол. Отсюда и название равноугольная. Он показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов. Отсюда и второе название: логарифмическая спираль. Независимо от Декарта она была открыта Э. Торричелли в 1644 г. Свойства логарифмической спирали исследовал Я. Бернулли (1692 г.), который называл её Spira mirabilis — « удивительная спираль ». . Её название предложено П. Вариньоном (1704 г.).

Рене Декарт Гравюра 1784 года, изображающая Иоганна и Якоба Бернулли, занятых решением геометрических задач

Логарифмическая спираль в математике
Эта кривая, такая простая по форме, кажется наполненной каким-то
непостижимым смыслом. Математики эту спираль называют
логарифмической. Представить её можно следующим образом.
Вокруг неподвижной точки (её называют полюсом) вращается прямая,
а по прямой движется точка-маркер. Маркер удаляется от полюса
со скоростью, пропорциональной пройденному расстоянию от него до полюса.
След, оставляемый маркером, и будет логарифмической спиралью.
В математике существует понятие логарифмической спирали. Спираль – это плоская кривая линия, многократно обходящая одну из точек на плоскости, эта точка называется полюсом спирали. Полюсом логарифмической спирали является начало координат. Спираль называется логарифмической, потому что уравнение, описывающее эту спираль, содержит логарифмы. Эта спираль имеет бесконечное множество витков, она не проходит через свой полюс. Логарифмическую спираль называют равноудаленной спиралью, это связано с тем, что в любой точке логарифмической спирали угол между касательной к ней и радиус – вектором сохраняет постоянное значение.
Уравнение логарифмической спирали в полярной системе координат имеет вид: p=а Ф , где, а>0
Переписав уравнение в виде ф= l oga p, мы видим, что величина полярного угла пропорциональна логарифму радиус-вектора. Отсюда и происходит название логарифмическая спираль.
Золотая Спираль Бернулли

Спираль в одну сторону развёртывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая.
Определение логарифмической спирали
Логарифмическая спираль — кривая, которая пересекает все лучи, выходящие из одной точки О, под одним и тем же углом.
Логарифмическая спираль — плоская кривая, описываемая точкой, движущейся по прямой, которая вращается около одной из своих точек О (полюса логарифмической спирали) так, что логарифм расстояния движущейся точки от полюса изменяется пропорционально углу поворота; логарифмическая спираль пересекает под постоянным углом все прямые, выходящие из полюса.
Уравнение кривой в полярных координатах:
коэффициенты. Расстояние между витками растет с увеличением угла поворота.
Логарифмическая спираль. Итак, что же такое логарифмическая спираль? Спираль – это плоская кривая линия, многократно обходящая одну из точек на плоскости, называемую полюсом спирали. Логарифмическая спираль является траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному расстоянию. Точнее, в логарифмической спирали углу поворота пропорционален логарифм этого расстояния.
Надо отметить, что многие ученые, философы и даже поэты преклонялись перед красотой и изяществом логарифмической спирали: не зря И.-В.Гете признал эту кривую символом жизни и развития человеческой души, а швейцарский математик Якоб Бернулли, пораженный способностью логарифмической спирали реагировать на любые изменения и трансформации полным восстановлением, сделал ее своеобразным символом воскресения.
Иоганн-Вольфганг Гёте считал: «Логарифмическая спираль есть символ жизни и духовного развития».
Свойство спирали. Якоб Бернулли открыл поразительное свойство спирали: кривая с «твёрдым» характером. Она не изменяется при сжатиях, растяжениях и поворотах.
Удивительное рядом … ( ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ там, где мы и не подозревали!)
1. Самолёт, вылетевший из какой-нибудь точки земного шара на север, через некоторое время окажется над Северным полюсом. Если же он полетит на восток, то, облетев параллель, вернётся в тот же пункт, из которого вылетел. Предположим теперь, что самолёт будет лететь, пересекая все меридианы под одним и тем же углом, отличным от прямого, т. е. держась, всё время одного и того же курса. Когда он облетит земной шар, то попадёт в точку, имеющую ту же долготу, что и точка вылета, но расположенную ближе к Северному полюсу. После следующего облёта он окажется ещё ближе к полюсу и, продолжая лететь указанным образом, будет описывать вокруг полюса сужающуюся спираль.
Уравнение этой спирали r=ae kv , где r — расстояние от произвольной точки М на спирали до выбранной точки О, v — угол между лучом ОМ и выбранным лучом Ох, a и k — постоянные. Решая его, получаем
Так как это уравнение связано с логарифмической функцией, то вычисленную по этой формуле спираль называют логарифмической.
2. Очень часто встречается логарифмическая спираль. Главная ее особенность заключается в том, что она пересекает все лучи, исходящие из центральной точки — полюса под одним и тем же углом. Если мы, находясь поблизости от Северного полюса, начнем все время двигаться на северо-запад, то мы будем кружить вокруг него по логарифмической спирали.
3. Три собаки сидят в вершинах равностороннего треугольника. По команде они вскакивают, и каждая собака устремляется к своей соседке справа. Все три собаки бегут с одинаковой скоростью. Каждая собака все время строго следует за той, за которой она гонится. Встречаются все три собаки в центре треугольника. Спрашивается, форму какой кривой имеет траектория каждой собаки?
Собаки, загоняющие друг друга в центр равностороннего треугольника, перемещаются вдоль логарифмических спиралей. Логарифмическую спираль можно определить как кривую, пересекающую все радиусы-векторы под одним и тем же углом. Пусть в условии задачи фигурируют не собаки, а три точки. Тогда каждая точка пройдет конечное расстояние (равное двум третям стороны треугольника), но для этого ей потребуется сделать бесконечное число витков вокруг полюса!
Если по условию задачи n собак (n>2) располагаются в вершинах правильного n-угольника, то и тогда траекторией движения каждой собаки всегда будет логарифмическая спираль. Случай n=2 соответствует тому, что две собаки бегут друг к другу по прямой. При п=бесконечность собаки носятся друг за другом по окружности. Итак, с помощью довольно грубого метода мы показали, что логарифмическая спираль вырождается в прямую и в окружность, когда угол, образованный ею с радиусом-вектором, равен соответственно 0° и 90°.
4. Кривая, пересекающая все земные меридианы и образующая с ними какой-нибудь постоянный угол (кроме прямого), тоже является логарифмической спиралью и имеет также специальное название: локсодрома (или линия постоянных углов). Если бы вы летели на северо-восток, строго выдерживая все время направление по компасу, то вы описали бы локсодрому, которая привела бы вас на Северный полюс. Так же как в задаче о собаках, ваш путь имел бы конечную длину, но (если бы вы были точкой) завершался бы в полюсе лишь после бесконечного числа витков вокруг него. Проекция траектории вашего полета на плоскость, касательную к поверхности Земли в полюсе, оказалась бы точной логарифмической спиралью.
5. Желающие немедленно наблюдать логарифмическую спираль в природе могут просто-напросто согнуть указательный палец, который тут же примет форму золотой логарифмической спирали — спирали, витки которой находятся по отношению друг к другу в пропорции золотого сечения.
6. Ч еловеческое ухо – это маленькое чудо

Улитка является органом, воспринимающим звук, в котором самой природой заложена л огарифмическая спираль.
Видео:Построение кривой в полярной системе координатСкачать

Логарифмическая спираль в природе
Особенности логарифмической спирали поражали не только математиков. Ее свойства удивляют и биологов, которые считают именно эту спираль своего рода стандартом биологических объектов самой разной природы.
Логарифмическая спираль — единственный тип спирали, не меняющей своей формы при увеличении размеров. Это свойство объясняет, почему логарифмическая спираль так часто встречается в природе.
• Спираль – одна из форм проявления движения, роста и развития жизни. По закону спирали развивается Галактика и живой организм, например, растения. Первым, кто отрыл, что растущее растение описывает спираль, был Чарльз Дарвин. Описывая спираль, вытягиваются стебли растений, двигаясь по спирали, раскрываются лепестки некоторых цветов, развертываются побеги папоротника.
• Спираль в то же время является в природе и сдерживающим началом, направленным на экономию энергии и материала.
• Лишь изменяя форму конструкции, придавая ей вид спирали, природа, таким образом, достигает в конструкции дополнительную жесткость и устойчивость в пространстве.
• Так, например, завиваются в спираль, приобретая этим дополнительную жесткость, тонкие и длинные стебли огурцов или тыквы, длинные листья рогоза и тонкие ножки грибов. Раковины простейших одноклеточных организмов форманифер и раковины моллюсков, закрученные в одной или разных плоскостях (турбоспирали) – это также проявление способа достижения наибольшей прочности при экономном расходовании материала. Благодаря завитой форме такие тонкостенные конструкции выдерживают большое гидродавление при погружении на глубину.


Царство животных предоставляет нам примеры спиралей раковин, улиток и моллюсков.
Например, по мере того как моллюск наутилус помпилиус растет в своей раковине, он создает камеры все просторнее и просторнее, а те, которые стали ему малы, запечатывает. Каждая прибавка в длине раковины влечет за собой и пропорциональное увеличение радиуса, поэтому общая форма раковины остается неизменной. То есть «домик» у наутилуса всю жизнь одинаковый, и моллюску не приходится потом, например, сдвигать центр тяжести раковины.


Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее аналогиям. Поэтому раковины многих моллюсков, улиток, закручены по логарифмической спирали.
. 


Раковина улитки. Немецкий биолог Румблер в 1910 году выдвинул теорию постоянного краевого угла при построении раковин улиток. Он исходил из того, что материал, из которого строятся раковины, вначале должен быть жидким, и в жидком состоянии попадает на край уже существующей части раковины где, естественно, всегда образуется постоянный краевой угол. Под этим углом жидкость затвердевает, и снова начинается та же игра. Раковина улитки представляет собой логарифмическую спираль.

По логарифмической спирали очерчены не только раковины. Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям.


То же свойство присуще и бараньим рогам – они тоже имеют форму логарифмической спирали, хотя и не лежат в одной плоскости, – и изгибу слоновьих бивней. Логарифмическая спираль, набирая размер, становится шире, расстояние между «витками» увеличивается по мере отдаления от центра – так называемого полюса. Причем поворот на равные углы увеличивает расстояние от полюса на равные промежутки.


Рога таких рогатых млекопитающих, как архары – горные козлы, закручены по логарифмической спирали.


Все эти формы указывают на природное явление: процесс накручивания связан с процессом роста. В самом деле, раковина улитки — это не больше, не меньше, чем конус, накрученный на себя. Если мы внимательно посмотрим на рост раковин и рогов, то заметим еще одно любопытное свойство: рост происходит только на одном конце. И это свойство сохраняет форму полностью уникальную среди кривых в математике, форму логарифмической, или равноугольной спирали.
И хотя физические законы роста у разных видов различны, математические законы, которые управляют ими, одинаковы: все они имеют в основе геометрическую спираль, самоподобную кривую.
В растительном мире примеры еще более бросаются в глаза, потому что у растения может быть бесконечное число спиралей, а не только одна спираль у каждого.
Замечено, что плоды деревьев, растений, несущие в себе зёрна будущего, выстраиваются по спиралям. Вспомним лесные шишки хвойных, полевые ромашки, огородные подсолнухи. В тугие спирали свёрнуты поднимающиеся из почвы молодые побеги.
Расположение семечек в любом подсолнечнике, чешуек в любом ананасе и другие разнообразные виды растений, простые ромашки… дают нам настоящий парад переплетающихся спиралей.
В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.


Если мы посмотрим сверху на любую сосновую шишку, увидим, что ее семена располагаются в виде большого числа спиралей.
И это неслучайно. Это не совпадение. Семена расположены оптимально, т. е. максимально используют пространство, и эта оптимизация пространства достигается за счет расположения по спирали.




Спирально закручиваются усики растений.


Постоянная форма логарифмической спирали любого размера прекрасно проявляется в природе и в очертаниях раковин микроскопических одноклеточных организмов под названием фораминиферы. Хотя спиральные ракушки в данном случае – структуры сложные, это не просто трубочка, рентгеновские изображения внутренней структуры ископаемых раковин этих существ показывают, что за много миллионов лет их рисунок – логарифмическая спираль – остался прежним.
Фораминиферы под микроскопом


Биологи заметили, что ночные бабочки пролетают большие расстояния, ориентируясь по параллельным лунным лучам. Они инстинктивно сохраняют постоянный угол между направлением полета и лучом света. Однако, встречая точечный источник света — свечу или лампочку, они начинают лететь по логарифмической спирали, приближаются к 

( Логарифмическую спираль называют равноугольной спиралью. Этот термин ввел в 1638 году французский математик и философ Рене Декарт (1596–1650), по имени которого названы числа, определяющие положение точки на плоскости относительно двух осей – декартова система координат.)

Слово «равноугольная» отражает другое уникальное качество логарифмической спирали. Если прочертить прямую линию из полюса к любой точке спирали, она пересечет кривую под одним и тем же углом. Этим качеством пользуются соколы, когда бросаются на добычу.
Почему хищник кружит над добычей
Мы так привыкли, что хищник кружит над своей добычей, что не только не задаемся вопросом, почему он это делает, но и в большинстве случаев, не замечаем, что на самом деле он выписывает функцию, называемую логарифмической спиралью.
Тайна того, почему хищные птицы в большинстве случаев летают именно по спирали, была открыта американцем Тукером. Согласно его заявлению, они делают это, чтобы максимально использовать их острое “поперечное” зрение.
Изучая соколов в Штате Колорадо, он и его коллег и обнаружили, что птицы, как только оказываются в радиусе 1.5 километров от добычи, почти всегда начинают летать по спирали. » Мы наблюдали эти спиральные полеты в течении нескольких лет, и никак не могли найти им объяснение» говорит Тукер.
Он подозревал, что объяснение кроется в особенностях зрения птицы. Исследования показали, что хищные пернатые наиболее четко видят объект тогда, когда голова повернута примерно на 40 градусов к нему. Но повернутая голова значительно затрудняет полет, и скорость его заметно падает, что было подтверждено следующим опытом: модели соколов и краснохвостах ястребов (в натуральную величину) он поместил в ветровой туннель. Датчики показали, что повернутая голова меняет направление полета, то есть для поддержания необходимого направления приходится прилагать значительно больше усилий, и скорость падает.
“Чтобы избегать этого”, заканчивает Тукер, “птицы держат голову прямо, но для более четкого изображения следуют по логарифмической спирали, то есть летят таким образом, чтобы один глаз был четко направлен на добычу”.. А поскольку спираль обладает свойством равноугольности, такая траектория позволяет птице, разгоняясь до предельных скоростей, не упускать добычу из виду. А увеличение скорости компенсирует длину спирального полета.
Природа обожает логарифмические спирали. Похоже, это ее любимый узор – она украшает им все подряд, от подсолнухов и ракушек до водоворотов, смерчей и гигантских спиральных галактик
Штормы и ураганы дают впечатляющие примеры логарифмических спиралей .
Циклоны (обычные и тропические) представляют собой крупномасштабные вихри диаметром: обычные от 1000 до 2000 км; тропические от 200 до 500 км и высотой от 2 до 20 км. Воздушные массы двигаются в области циклона по спирали, закручивающейся к его центру (против часовой стрелки в северном полушарии, в южном наоборот) со скоростью: — обычные не более 50-70 км/ч; — тропические 400-500 км/ч
В центре циклона давление воздуха ниже чем на периферии, именно поэтому, двигаясь по спирали, воздушные массы стремятся к центру, где они затем подымаются вверх, порождая сильную облачность.
В центре тропического циклона есть область низкого давления с высокой температурой, диаметром 10-40 км, где царит затишье – глаз тайфуна.


По логарифмической спирали формируется тело циклона


Глаз бури, тропический шторм Изабель Тайфун Смерч
1 
1 — Тропический циклон Кейт, снимок с международ. Космич. Станции; 2 — Тайфун Вонгфонг над Японией 2014 год
Тайфун — это наиболее опасное и разрушительное природное явление на нашей планете. Тайфун представляет собой мощный атмосферный вихрь, ЗАКРУЧИВАЮЩИЙСЯ ПО СПИРАЛИ, с пониженным атмосферным давлением в середине. Из-за больших изменений давления внутри тайфуна скорость ветра достигает огромных значений (около 400 км/ч). В тайфуне наблюдается интенсивный подъем воздуха и образование мощных кучево-дождевых облаков, из которых выпадает огромное количество осадков. Они способны вызвать наводнение. В центре тайфуна ветер почти отсутствует и уменьшена облачность — это «глаз бури».
Логарифмические спирали в природе могут достигать гигантских размеров. С этой точки зрения наиболее впечатляющим примером является спиральная структура галактик. Этот факт представляет собой не меньшую задачу, чем проблема их строения. Известно, что галактики состоят из горячих звезд и скоплении газа, которые в результате вращения галактики распределяются вдоль ветвей логарифмической спирали. Представьте себе скопление биллионов звезд, которое вращается в пространстве подобно огромной детской вертушке. Слабое белое свечение Млечного Пути объясняется тем, что мы смотрим на него как бы сбоку, сквозь две огромные ветви нашей собственной Галактики. Наблюдения показывают, что у центра Галактики ветви спирали вращаются значительно быстрее, чем на границе, то есть они должны были бы быстро раскрутиться и, может быть, даже вообще уничтожиться. Однако галактики, как правило, сохраняют спиральную структуру, что говорит о том, что ветви вовсе не раскручиваются. Существует теория, согласно которой, с одной стороны, ветвь непрерывно обогащается светящимся газом, а с другой — он испаряется, в результате чего ветви галактики имеют вполне определенную форму, характерную для данной галактики*.
Многие галактики, закручены по логарифмической спирали




Как ни удивительно, та же самая спиральная кривая, какую мы наблюдаем у ракушек одноклеточных фораминифер и в сердцевине подсолнуха, та же, которая направляет полет сокола, обнаруживается и в «звездных системах, группирующихся в одной плоскости, наподобие Млечного пути», о которых философ Иммануил Кант (1724–1804) размышлял задолго до того, как их удалось пронаблюдать. Эти системы было принято называть «островные Вселенные» – гигантские галактики, в которых таких звезд, как наше Солнце, сотни миллиардов. Наблюдения на орбитальном телескопе им. Э. Хаббла показали, что в наблюдаемой Вселенной примерно сто миллиардов галактик, многие из них спиральные. Трудно придумать более удачную иллюстрацию к величественному видению английского поэта, художника и мистика Уильяма Блейка (1757–1827), писавшего:
В одном мгновенье видеть вечность,
Огромный мир – в зерне песка,
В единой горсти – бесконечность
И небо – в чашечке цветка.
Звездные галактики. 1845 г. английский астроном лорд Росс (Уильям Парсонс) с помощью телескопа со 180-сантиметровым металлическим зеркалом обнаружил целый класс туманностей в виде логарифмической спирали, самым ярким примером которых явилась туманность в созвездии Гончих Псов. Природа этих туманностей была установлена лишь в первой половине XX столетия. Спиральные туманности — это огромные звездные системы, сравнимые с нашей Галактикой. С тех пор их и стали называть галактиками. Немало усилий пришлось приложить астрономам, чтобы описать свойства спиральных галактик с помощью логарифмов. В спиральных ветвях наблюдается повышение плотности, как звезд, так и межзвездного вещества — пыли и газа. Повышенная плотность газа ускоряет образование и последующее сжатие газовых облаков и тем самым стимулирует рождение новых звезд. Поэтому спиральные ветви являются местом интенсивного звездообразования.

Галактика в Созвездии Гончие псы
Почему же галактики так часто имеют форму спирали? Спиральные галактики вроде нашего Млечного пути – это относительно плоский диск, вроде блина, состоящий из газа, звездной пыли и звезд. Весь галактический диск вращается вокруг центра галактики. Например, по соседству от Солнца орбитальная скорость вокруг центра Млечного пути составляет примерно 225 километров в секунду, а на полный оборот понадобится около 225 миллионов лет. На других расстояниях от центра и скорость иная – чем ближе к центру, тем больше, а на дальних дистанциях меньше, то есть галактический диск вращается не как твердый диск, а дифференциально. Если посмотреть на диск сверху, у спиральных галактик видны спиральные рукава, которые начинаются вблизи от центра и расходятся в разные стороны по большей части диска, как на рис, где изображена галактика Водоворот. Спиральные рукава – это те области галактического диска, где рождается много новых звезд.
Золотой двухрукавный спиральный каркас Солнечной системы (для внутренних планет).
Поскольку новые звезды самые яркие, спиральную структуру других галактик нам видно издалека. Главный вопрос, на который надо было ответить астрофизикам, состоял вот в чем: как спиральным рукавам удается так долго сохранять форму? Ведь внутренние части диска вращаются быстрее внешних, так что любой крупномасштабный узор, так или иначе связанный с материалом диска, то есть со звездами, долго бы не удержался. Спиральная структура, привязанная к одному и тому же скоплению звезд и облаков газа, неизбежно нарушилась бы, а наблюдениями это не подтверждается. Долголетие спиральных рукавов объясняется волнами плотности – волнами сжатия газа, проходящими по галактическому диску, – которые по пути сжимают газовые облака и способствуют зарождению новых звезд. Спиральный узор, который мы наблюдаем, это попросту проявление тех областей диска, где плотность выше средней и много новых звезд. Поэтому узор постоянно воссоздается и не нарушается.
Подобное же положение дел мы наблюдаем поблизости от огороженного участка дорожных работ на крупном шоссе. Плотность машин поблизости от закрытого участка выше, потому что водители вынуждены там притормаживать. Если сделать фотографию шоссе с птичьего полета с большой выдержкой, можно зафиксировать плотность пробки поблизости от места ремонта. Волна плотности машин не связана с каким-то конкретным набором автомобилей, точно так же и спиральный узор не связан с тем или иным «куском» материала диска. Еще одна общая черта – тот факт, что волна плотности движется через диск медленнее движения самих звезд и газа, точно так же как скорость, с которой участок дорожных работ перемещается вдоль шоссе, как правило, гораздо медленнее, чем двигаются отдельные автомобили, которым ничто не мешает.
Движущая сила, которая отражает движение звезд и газовых облаков и порождает спиральную волну плотности (аналогично тому, как дорожные работы ограничивают движение автомобилей, оставляя им меньше полос) – это сила тяготения, вызванная тем обстоятельством, что распределение материи в галактике не полностью симметрично. Например, набор эллиптических орбит вокруг центра галактики (рис а), в котором каждая орбита несколько возмущена (повернута), причем сила возмущения меняется в зависимости от расстояния от центра, приводит к возникновению спирального узора (рис. b).
В сущности, надо радоваться, что сила тяготения ведет себя в нашей Вселенной именно так, а не иначе. Согласно закону всемирного тяготения Ньютона, всякая масса притягивает всякую другую массу и сила притяжения уменьшается с расстоянием. В частности, увеличение расстояния вдвое ослабляет силу тяготения в четыре раза (сила тяготения обратно пропорциональна квадрату расстояния). Ньютоновы законы движения показывают, что в результате зависимости силы тяготения от расстояния орбиты планет вокруг Солнца имеют форму эллипсов. А теперь представьте себе, что было бы, живи мы во Вселенной, где гравитация ослабевает при удвоении расстояния с коэффициентом восемь, а не четыре – то есть если бы сила тяжести уменьшалась в зависимости от куба расстояния. В такой Вселенной законы Ньютона предсказывали бы одну-единственную возможную орбиту для планеты – логарифмическую спираль. Иначе говоря, Земля либо по спирали устремилась бы к Солнцу, либо умчалась бы в космос.
Млечный Путь (спиральная галактика с перемычкой) узнается очень быстро благодаря широкой и вытянутой белой линии, напоминающей молочный след. Галактика простирается на 100000 световых лет в диаметре. От выпуклости в центре исходят 4 крупных спиральных рукава. Этот тип представляет 2/3 вселенских галактик.
В отличие от привычной спирали, экземпляры с перемычкой вмещают стержень в центре с двумя ответвлениями. У нашей галактики есть два главных рукава и два второстепенных. В рукаве Ориона расположена наша система.
Положение Солнца в галактике Млечный Путь
Между двумя главными рукавами находится рукав Ориона, в котором на 27000 световых лет от центра расположена наша система. Жаловаться на удаленность не стоит, ведь в центральной части притаилась сверхмассивная черная дыра (Стрелец А*).
Структура Млечного Пути: вид сбоку
Галактика Whirlpool («Водоворот») является классической представительницей спиральных галактик. В ее рукавах множество ярких молодых звезд, и повернута к нам она таким образом, что все это хорошо видно. Галактика «Водоворот» расположена в созвездии Гончих Псов и удалена от Земли на 31 миллион световых лет. Справа от «Водоворота» отчетливо видна карликовая галактика NGC 5195, которая на протяжении сотен миллионов лет как бы скользит по краю «Водоворота».
Галактика M64 (др. названия: NGC 4826) – артистическая аллегория Спящей красавицы по имени Черный Глаз (ее другое название – Глаз Дьявола) — спиральная галактика, которая находится в созвездии Волосы Вероники. Расположена на расстоянии примерно 18,3 миллионов световых лет (5,6 млн парсек) от Земли. Диаметр спиральной галактики Черный Глаз примерно 56 000 световых лет, что почти в два раза меньше диаметра Млечного Пути.

Появилась она в результате столкновения двух галактик, более миллиарда лет назад. Они вращались в разные стороны, вследствие этого газопылевой диск, который находится во внутренней части галактики, стал вращаться в противоположную сторону, относительно звезд и скоплений газа. Так как внешние слои галактики обращаются в противоположном направлении относительно центральной выпуклости – это признак поглощения большой галактикой малой галактики, для которой первая стала уютной колыбелью.
Своим названием галактика обязана огромному пылевому облаку, которое полностью поглощает свет, в результате чего ядро выглядит особенно ярко. Также там постоянно происходит процесс формирования новых звезд, благодаря наличию огромного количества газа и пыли. Особенно выделяются среди них ярко-голубые молодые звезды, окруженные облаками розовой пыли, которые, в основном, состоят из светящегося ионизированного водорода.
Порадуйтесь внеземной красоте нашего мира.
Столкновения между газом во внутренних и внешних областях создают горячие голубые звезды и розовые эмиссионные туманности.
В следствие столкновения малой и большой галактик мы можем наблюдать спиральную галактику, нарядившуюся гирляндами из миллионов ярчайших розовых и голубых огоньков.

Видео:Полярная система координатСкачать

Юпитер, который мы недавно узнали
« Равнодушный глаз Сатурна» — шторм, закручивающийся по логарифмической спирали, который длится сотни лет, вдобавок вписывается в правильный шестиугольник.
Понемногу мы узнаем все новую и новую информацию о Юпитере — газовом гиганте нашей Солнечной системы, и в этом нам активно помогает межпланетный зонд «Юнона». Благодаря ему ученые, наконец, нашли источники штормов планеты, расположенные под непрозрачной атмосферой, и открыли поразительную геометрическую схему циклонов, расположенных у южного и северного полюсов.
На каждом полюсе планеты находится по циклону с диаметром несколько тысяч километров — и это не особо удивляет, с учетом того, что планета — газовый гигант. Но каждый из этих циклонов окружен штормами одинакового размера, расположенными в вершинах правильных многоугольников — восьмиугольника на северном полюсе и пятиугольника на южном.
«Мы действительно не понимаем, почему это происходит, и почему они собираются там таким геометрическим образом», — говорит Болтон. «Удивительно, что природа способна создать что-то подобное».
Вот так выглядят глаза бури этих циклонов (то есть их центральные области — прим. перев.):

На северном полюсе доминирует центральный циклон, окруженный восемью циклонами диаметром от 4000 до 4600 километров.
Южный полюс также имеет центральный циклон и окружен пятью циклонами диаметром от 5600 до 7000 километров. Эти штормы расположены так же, как таинственный северный полярный шестиугольник бурь на Сатурне .
Что наиболее поразительно в этих циклонах, так это то, как они плотно «упакованы» в полюса Юпитера. Они расположены прямо друг напротив друга, и их спиральные вихри, ( закручивающиеся по логарифмической спирали) даже показывают, что они касаются друг друга, но никогда не сливаются.
Рассмотренные примеры дают нам наиболее впечатляющие примеры спиральной структуры галактик, которых во Вселенной более 2/3 всех галактических систем .
Спираль в живописи
Логарифмические линии в природе замечают не только математики, но и художники. Геометрические мотивы нередко присутствуют в картинах великих живописцев. Художник при этом часто действует интуитивно, а искусствовед, исследуя композицию, выявляет её основу, приводя картину к упрощенной геометрической схеме.
Проанализируем, как часто используют художники логарифмическую спираль, для изображения сложных движений.
1. Одним из примеров логарифмической спирали в живописи является композиция Карла Брюллова — «Последний день Помпеи». Сюжет картины также всем хорошо знаком. Конфликт могущественных сил природы и беззащитность человека. Карл Брюллов задумал «Последний день Помпеи», как массовую сцену реального исторического события, в которой главным героем был народ. Смысл картины воплощается в передаче психологии массы.
В центре картины выделяются две группы: мужчина, прикрывающий собой жену и двух маленьких детей, защищающий своих родных от разгула стихии, и группа коленопреклонённой молодой женщины с двумя детьми.
Картины, в которых изображаются активные действия персонажей, развитие, конфликты, чаще всего строятся по принципу спирали. Интересно было проследить, как справедлив этот закон для такого трагического сюжета: изображение конфликта незащищённого человека и разбушевавшегося Везувия. Начало спирали можно совместить с глазами юноши, наблюдающего из толпы весь ужас происходящего. Вот что получилось в результате наложения спирали на картину. Спираль соединяет лицо молодого человека и жерло грозного Везувия, все персонажи трагедии, размещены по линии золотой спирали, а все сюжетные группы, вписываются в квадраты или на стороны квадратов, на которых строится золотая спираль.

Картина Брюллова «Последний день Помпеи»
Если золотое сечение использовалось художниками для ощущения уравновешенности, покоя, то золотая (логарифмическая) спираль, напротив, применялась для выражения тревожных, бурно развивающихся событий. Картина Карла Павловича Брюллова «Последний день Помпеи», как раз отличается динамизмом и драматизмом сюжета. На картине проведена золотая спираль, по которой располагаются основные фигуры композиции.
Так же мы наблюдаем это явление в таких произведениях, как: «Избиение младенцев» Рафаэля, «Боярыня Морозова» Сурикова, «Благовещение» Боттичелли.
2. 
📸 Видео
§6 Спираль АрхимедаСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Логарифмическая спиральСкачать

Полярная система координат.Скачать

Полярная Система Координат.Скачать

Площадь фигуры, заданной в полярной системе координатСкачать

Длина параболы и спирали Архимеда: что у них общего?Скачать

Скорость и ускорение точки в полярных координатахСкачать

Спираль Архимеда построениеСкачать

Логарифмическая спираль и числа Фибоначчи в творчестве Н.К.РерихаСкачать

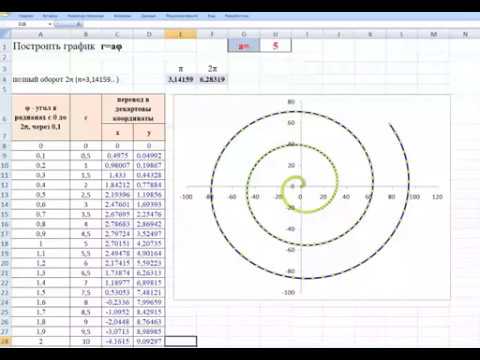
графики спираль Архимера и розы Гранди в ExcelСкачать
Оператор Лапласа в полярных координатахСкачать

Почему простые числа образуют спирали? [3Blue1Brown]Скачать
![Почему простые числа образуют спирали? [3Blue1Brown]](https://i.ytimg.com/vi/DxntHp7-wbg/0.jpg)
Площади 12Скачать

Способы задания функций. Неявная функция. Функция заданная параметрически и в полярных координатах.Скачать

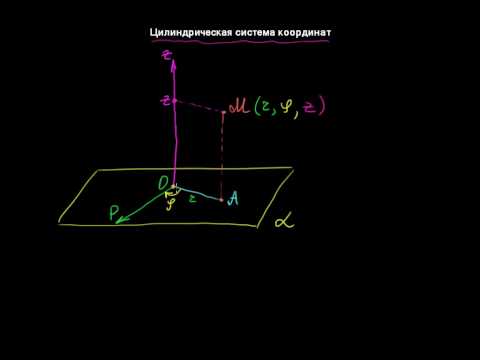
§55 Цилиндрическая система координатСкачать