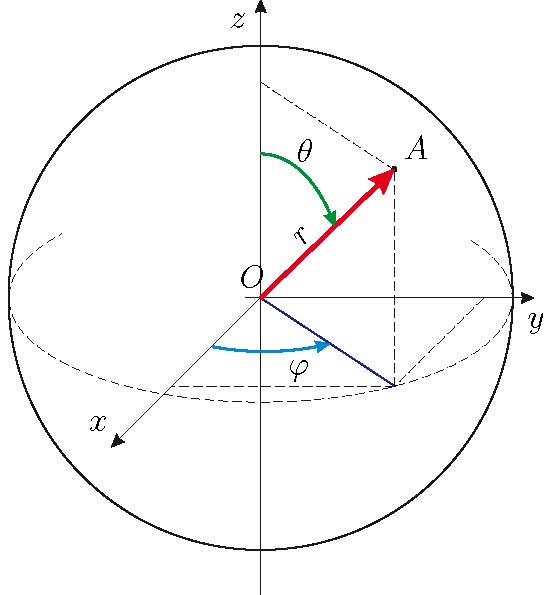
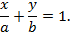Уравнение линии в сферической системе координат (5 видео)

Сферические координаты (сферическая система координат)

Для введения сферической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом ( начало сферической системы координат ) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием до начала координат, полярным углом точки — ортогональной проекции точки на основную плоскость, и углом между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки — это упорядоченная тройка чисел – радиус , долгота и широта . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом и широтой для положительной части оси и для отрицательной ее части. Начало координат задается нулевым значением радиуса . Иногда вместо угла широтой называют угол , принимающий значения .

Со сферической системой координат можно связать прямоугольную систему координат (рис.2.36,б), у которой начало и базисные векторы совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат ( связанную с данной прямоугольной ).

Содержание

Переход от сферических координат к декартовым (прямоугольным)
Сферическая система координат в пространстве.
Формулы аналитической геометрии в пространстве
📽️ Видео

Видео:§56 Сферическая система координатСкачать

Переход от сферических координат к декартовым (прямоугольным)

Получим формулы, связывающие между собой прямоугольные координаты точки и её сферические координаты . По рис.2.36,б получаем

Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам

Формулы (2.22) определяют долготу с точностью до слагаемых , где . При из них следует, что . Главное значение долготы находится по формулам (см. рис.2.29).

Пример 2.13. В сферической системе координат :

а) построить координатные поверхности ;

б) найти сферические координаты точки , если известны её прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны её сферические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении радиуса , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении широты , является конус, ось которого совпадает с осью аппликат, а вершина — с началом координат. При получаем основную плоскость. На рис.2.37 изображены конус и основная плоскость .

б) Найдем сферические координаты точки . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем

Видео:Полярная система координатСкачать

Сферическая система координат в пространстве.

(r, θ, ϕ) — сферические координаты точки A. Формулы перехода:

Диапазоны изменения значений координат:

(mod 2).

6. УРАВНЕНИЯ ЛИНИЙ НА ПЛОСКОСТИ.

Уравнение линии на плоскости — уравнение вида

каждое решение (x, y) которого представляет собой координаты некоторой точки линии, причем для каждой точки линии найдется некоторое решение данного уравнения.

6.1. Уравнения прямых на плоскости.Уравнение прямой — линейное уравнение:

Уравнение можно умножить на любое ненулевое число.

1. Уравнение с угловым коэффициентом:

k — угловой коэффициент прямой:

2. Уравнение прямой «в отрезках»:

6.2. Окружность.Окружность радиуса R с центром в начале координат:

Окружность радиуса R с центром в точке C(a, b):

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Формулы аналитической геометрии в пространстве

$d=sqrt$

НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$
$l=cosalpha=frac$, $m=cosbeta=frac$, $n=cosgamma=frac$

где $alpha,beta,gamma$ углы, которые линия $P_1P_2$ образовывает с положительными осями $x,y,z$ соответственно, а $d$ определено на рисунке вверху.

ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
$cos^2alpha+cos^2beta+cos^2gamma=1$ или $l^2+m^2+n^2=1$

НАПРАВЛЯЮЩИЕ ЧИСЛА
Числа $L,M,N$, которые есть пропорциональны к направляющим косинусам $l, m, n$ называются направляющими числами. Отношение между ними

Это также действительно, если $l, m, n$ заменяются на $L, M, N$ соответственно.

УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$

Это также действительно если $l, m, n$ заменяются на $L, M, N$ соответственно.

УГОЛ $phi$ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ $l_1, m_1, n_1$ И $l_2, m_2, n_2$
$cosphi=l_1l_2+m_1m_2+n_1n_2$

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$Ax + By + Cz + D = 0$ [$A, B, C, D$ — константы]

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$

$beginx-x_1 & y-y_1 & z-z_1\ x_2-x_1 & y_2-y_1 & z_2-z_1\ x_3-x_1 & y_3-y_1 & z_3-z_1end=0$

$begin y_2-y_1 & z_2-z_1\ y_3-y_1 & z_3-z_1end(x-x_1)$ $+begin z_2-z_1 & x_2-x_1\ z_3-z_1 & x_3-x_1end(y-y_1)$ $+begin x_2-x_1 & y_2-y_1\ x_3-x_1 & y_3-y_1end(z-z_1)=0$

где $a, b, c$ есть пересечения на осях $x, y, z$ соответственно.

Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости $Ax + By + Cz + D = 0$ есть $A, B, C$.

где знак выбирается так, что расстояние не является отрицательным.

НОРМАЛЬНОЕ УРАВНЕНИЯ ПЛОСКОСТИ
$xcosalpha+ycosbeta+zcosgamma=p$

где $p$ = перпендикулярному расстоянию от $O$ к плоскости в $P$ и $alpha, beta, gamma$ есть углами между $OP$ и положительными осями $x, y, z$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ
$left<beginx=x’+x_0\ y=y’+y_0\ z=z’+z_0endright.$ $left<beginx’=x-x_0\ y’=y-y_0\ z’=z-z_0endright.$

где $(x, y, z)$ — старые координаты [т.e. координаты относительно системы xyz], $(x’, y’, z’)$ — новые координаты [относительно системы $x’y’z’$] и $(x_0,y_0,z_0)$ координаты нового центра $O’$ относительно старой координатной системы $xyz$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ВРАЩЕНИИ

где центры систем $xyz$ и $x’y’z’$ находятся в одной точке и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ

$left<beginx=l_1x’+l_2y’+l_3z’+x_0\ y=m_1x’+m_2y’+m_3z’+y_0\ z=n_1x’+n_2y’+n_3z’+z_0endright.$

$left<beginx’=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\ y’=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\ z’=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)endright.$

где $O’$ системы $x’y’z’$ имеет координаты $(x_0,y_0,z_0)$ относительно системы $xyz$ и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, z)$
Точка $P$ может быть определена как цилиндрическими координатами $(r, theta, z)$, так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя координатами есть

СФЕРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, phi)$
Точка $P$ может быть определена как сферическими координатами $(r, theta, phi)$ так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя кординатами есть

$left<beginx=rsinthetacosphi\ y=rsinthetasinphi\ z=rcosthetaendright.$