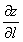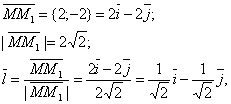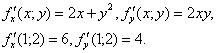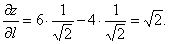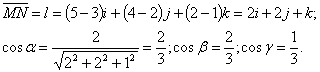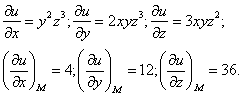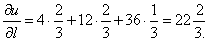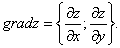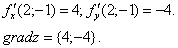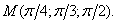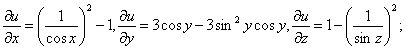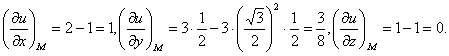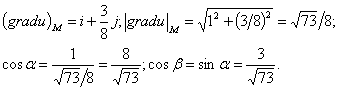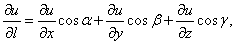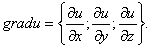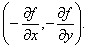Уравнение линии уровня через точку

Видео:Нахождение градиента функции в точкеСкачать

Линии и поверхности уровня

Содержание:

Видео:Поверхности и линии уровняСкачать

Линии и поверхности уровня

Понятие линии и поверхности уровня:

Для характеристики функций двух переменных вводится понятие линий уровня.

Определение 2. Линией уровня функции z = f (x, y) называется совокупность всех точек на плоскости Oxy, для которых выполняется условие f (x, y) = C.

Линии уровня можно получить, пересекая поверхность z = f (x, y) плоскостями z = C, где С = соnst.

Пример 1. Найти линии уровня функции z = x 2 + y 2 .

Решение.
Пусть z = C. x 2 + y 2 = C (C ≥ 0),

В этом случае линиями уровня является множество концентрических окружностей с центром в начале координат и радиусом С (рис. 2) .Аналогично вводится понятие поверхности уровня для функции трех переменных u = f (x, y, z), (f (x, y, z) = C).

Пример 2. Найти поверхности уровня функции u = x 2 + y 2 + z 2 .

Решение. Пусть u = C. Тогда x 2 + y 2 + z 2 = C (C ≥ 0) — это множество сфер с центром в точке O(0; 0; 0) и радиусом C.

Поверхности второго порядка

Наиболее изучены поверхности в курсе аналитической геометрии — поверхности второго порядка. В общем случае уравнение такой поверхности имеет вид:
a₁₁ x 2 + 2a₁₂ xy + a₂₂ y 2 + 2a₁₃ xz + 2a₂₃ yz + a₃₃ z 2 + 2a₁₄ x + 2a₂₄ y + 2a₃₄ z + a₄₄ = 0.

В зависимости от значений коэффициентов получают различные поверхности второго порядка.

Например:
1) — конус;

2) — полусфера;

Рис. 4.

3) — эллиптический параболоид;

Рис. 5.

4) — гиперболический параболоид;

рис.6

5) — трехосный эллипсоид.

Рис. 7.

Для изучения поверхностей в трехмерном пространстве применяется метод сечений. Суть этого метода такова: пересекаем заданную поверхность плоскостями x = C₁, y = C₂, z = C₃. В результате получим некоторые кривые, характеризующие поверхность.

Пример 3. z = x 2 + y 2 . Пусть z = C₁ (C₁ ≥ 0). Получим уравнение x 2 + y 2 = C₁ (уравнение окружности). Положим y = C₂ , тогда — уравнение параболы в плоскости Оxz, которая смещена на единиц вверх по оси Oz. Положим x = C₃ , получим уравнение
Получили уравнение параболы в плоскости Оyz, которая смещена на единиц вверх по оси Оz. Из этих исследований вытекает, что графиком функции z = x 2 + y 2 является параболоид вращения вокруг оси Оz.

Видео:Математика без Ху!ни. Функции нескольких переменных. Область определения. Линии уровня.Скачать

Гиперповерхности уровня

Пусть задана функция от n переменных u = f (x₁, x₂, . x_n) . Если положить u = C, то получим уравнение f (x₁, x₂, . x_n) = C, которое называется уравнением гиперповерхности уровня в пространстве R n . Например: Если u = C, то уравнение является уравнением гиперсферы в R n с центром в точке O (0,0, . 0) и радиусом .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:1 Линии уровняСкачать

5.6. Производная по направлению. Градиент. Линии уровня функции

Определение. Предел отношения 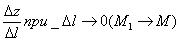, если он существует, называется Производной функции Z=F(M) в точке M(X; Y) по направлению вектора L .

Обозначение.

Если функция F(M) дифференцируема в точке М(х; у), то в точке М(х; у) существует производная по любому направлению L, исходящему из М; вычисляется она по следующей формуле:

(8)

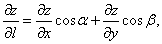
Где Cos И Cos — направляющие косинусы вектора L.

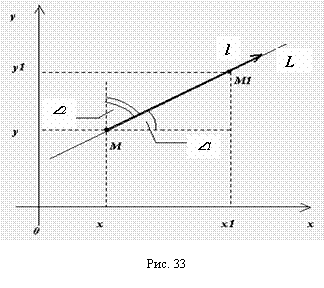
Пример 46. Вычислить производную функции Z=X2+Y2X в точке М(1; 2) по направлению вектора ММ1, где М1 – точка с координатами (3; 0).

Решение. Найдем единичный вектор L, имеющий данное направление:

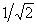
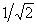
Откуда Cos=; Cos=-.

Вычислим частные производные функции в точке М(1; 2):

По формуле (8) получим

Пример 47. Найти производную функции U = Xy2Z3 в точке М(3; 2; 1) В направлении вектора MN, где N(5; 4; 2).

Решение. Найдем вектор 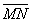и его направляющие косинусы:

Вычислим значения частных производных в точке М:

Следовательно,

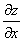
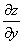
Определение. Градиентом Функции Z=F(M) в точке М(х; у) называется вектор, координаты которого равны соответствующим частным производным и, взятым в точке М(х; у).

Обозначение.

Решение. Находим частные производные: 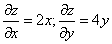и их значения в точке М(2; -1):

Пример 49. Найти величину и направление градиента функции 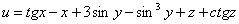в точке

Решение. Найдем частные производные и вычислим их значения в точке М:

Аналогично определяется производная по направлению для функции трех переменных U=F(X, Y, Z), выводятся формулы

Вводится понятие градиента

Подчеркнем, что Основные свойства градиента функции важнее для анализа экономических оптимизационных задач: в направлении градиента функция возрастает. В экономических задачах находят применение следующие свойства градиента:

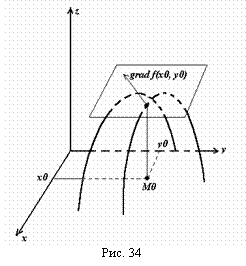
1) Пусть задана функция Z=F(X, Y), имеющая частные производные в области определения. Рассмотрим некоторую точку М0(х0, у0) из области определения. Значение функции в этой точке пусть равно F(X0, Y0). Рассмотрим график функции. Через точку (X0, Y0, F(X0, Y0)) трехмерного пространства проведем плоскость, касательную к поверхности графика функции. Тогда градиент функции, вычисленный в точке (х0, у0), рассматриваемый геометрически как вектор, приложенный в точке (X0, Y0, F(X0, Y0)), будет перпендикулярен касательной плоскости. Геометрическая иллюстрация приведена на рис. 34.

2) Градиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого возрастания функции в точке М0. Кроме того, любое направление, составляющее с градиентом острый угол, является направлением роста функции в точке М0. Другими словами, малое движение из точки (х0, у0) по направлению градиента функции в этой точке ведет к росту функции, причем в наибольшей степени.

Рассмотрим вектор, противоположный градиенту. Он называется Антиградиентом. Координаты этого вектора равны:

Антиградиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого убывания функции в точке М0. Любое направление, образующее острый угол с антиградиентом, является направлением убывания функции в этой точке.

3) При исследовании функции часто возникает необходимость нахождения таких пар (х, у) из области определения функции, при которых функция принимает одинаковые значения. Рассмотрим множество точек (X, Y) из области определения функции F(X, Y), таких, что F(X, Y)=Const, где запись “Const” означает, что значение функции зафиксировано и равно некоторому числу из области значений функции.

Линии уровня геометрически изображаются на плоскости изменения независимых переменных в виде кривых линий. Получение линий уровня можно представить себе следующим образом. Рассмотрим множество С, которое состоит из точек трехмерного пространства с координатами (X, Y, F(X, Y)=Const), которые, с одной стороны, принадлежат графику функции Z=F(X, Y), с другой — лежат в плоскости, параллельной координатной плоскости ХОУ, и отстоящей от неё на величину, равную заданной константе. Тогда для построения линии уровня достаточно поверхность графика функции пересечь плоскостью Z=Const и линию пересечения спроектировать на плоскость ХОУ. Проведенное рассуждение является обоснованием возможности непосредственно строить линии уровня на плоскости ХОУ.

Определение. Множество линий уровня называют Картой линий уровня.

Хорошо известны примеры линий уровня – уровни одинаковых высот на топографической карте и линии одинакового барометрического давления на карте погоды.

Определение. Направление, вдоль которого скорость увеличения функции максимальна, называется «предпочтительным» направлением, или Направлением наискорейшего роста.

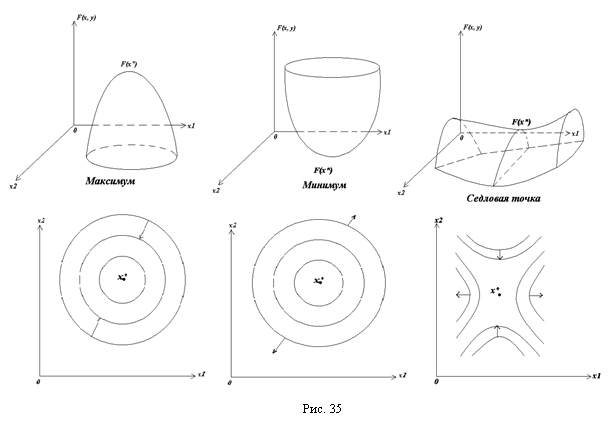
«Предпочтительное» направление задается вектором-градиентом функции. На рис. 35 изображены максимум, минимум и седловая точка в задаче оптимизации функции двух переменных при отсутствии ограничений. В нижней части рисунка изображены линии уровня и направления наискорейшего роста.

Решение. Уравнение семейства линий уровня имеет вид X2+Y2=C (C>0). Придавая С различные действительные значения, получим концентрические окружности с центром в начале координат.

Построение линий уровня. Их анализ находит широкое применение в экономических задачах микро — и макроуровня, теории равновесия и эффективных решений. Изокосты, изокванты, кривые безразличия – это все линии уровня, построенные для разных экономических функций.

Пример 51. Рассмотрим следующую экономическую ситуацию. Пусть производство продукции описывается Функцией Кобба-Дугласа F(X, Y)=10х1/3у2/3, где Х – количество труда, У – количество капитала. На приобретение ресурсов выделено 30 у. ед., цена труда составляет 5 у. ед., капитала – 10 у. ед. Зададимся вопросом: какой наибольший выпуск можно получить в данных условиях? Здесь под «данными условиями» имеются в виду заданные технологии, цены на ресурсы, вид производственной функции. Как уже отмечалось, функция Кобба-Дугласа является монотонно возрастающей по каждой переменной, т. е. увеличение каждого вида ресурса ведет к росту выпуска. В данных условиях ясно, что увеличивать приобретение ресурсов можно до тех пор, пока хватает денег. Наборы ресурсов, стоимость которых составляет 30 у. ед., удовлетворяют условию:

Т. е. определяют линию уровня функции:

С другой стороны, с помощью линий уровня Функции Кобба-Дугласа (рис. 36) можно показать возрастание функции: в любой точке линии уровня направление градиента – это направление наибольшего возрастания, а для построения градиента в точке достаточно провести касательную к линии уровня в этой точке, построить перпендикуляр к касательной и указать направление градиента. Из рис. 36 видно, что движение линии уровня функции Кобба-Дугласа вдоль градиента следует производить до тех пор, пока она не станет касательной к линии уровня 5х + 10у = 30. Таким образом, с помощью понятий линии уровня, градиента, свойств градиента можно выработать подходы к наилучшему использованию ресурсов с точки зрения увеличения объемов выпускаемой продукции.

Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Компьютерный чертеж. Выполним

Линии уровня и градиент функции двух переменных

Линией уровня функции называется множество точек из области определения на плоскости , для которых значение функции постоянно и равно , то есть

Построить график функции . Записать уравнение линии уровня, проходящей через точку .

Графиком линейной функции двух переменных является плоскость в пространстве. Для функции график представляет собой плоскость, проходящую через точки , , .

Линиями уровня функции являются параллельные прямые, уравнение которых или или .

Найдем уравнение линии уровня, проходящей через точку , для этого подставим координаты точки в уравнение и найдем значение параметра :

уравнение линии уровня, проходящей через точку имеет вид

🎬 Видео

9 класс, 6 урок, Уравнение окружностиСкачать

Линии уровня и поверхности уровня функции многих переменныхСкачать

2. Область определения функции двух переменныхСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Составляем уравнение прямой по точкамСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Линии уровняСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

10. ФНП. Градиент и производная по направлению функции двух переменных.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Уравнение прямой на плоскости. Решение задачСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать