Уравнение линии пересечения двух цилиндров

Содержание:

Возможные случаи пересечения криволинейных поверхностей:

Существуют четыре варианта пересечения двух поверхностей.

Видео:Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

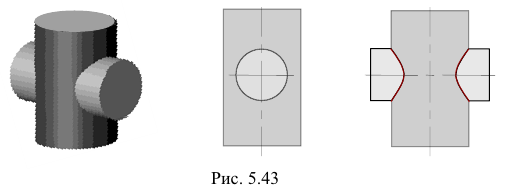
Проницание

Все образующие первой поверхности (цилиндра) пересекаются со второй поверхностью, но не все образующие второй поверхности пересекаются с первой. В этом случае линия пересечения поверхностей распадается на две замкнутые кривые линии (рис. 5.43).

Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

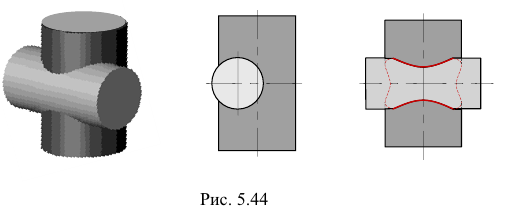
Врезание

Не все образующие той и другой поверхности пересекаются между собой. В этом случае линия пересечения — одна замкну­ тая кривая линия (рис. 5.44).

Видео:Пересечение двух цилиндров. Инженерная графикаСкачать

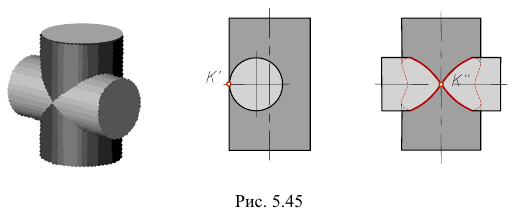
Одностороннее касание

Все образующие одной поверхности пересекаются со второй, но не все образующие второй поверхности пересекаются с первой. Поверхности имеют в одной точке (точка К на рис. 5.45) общую плоскость касания. Линия пересечения распадается на две замкнутые кривые линии, пересекающиеся в точке касания.

Видео:Линия пересечения конуса и цилиндра (метод концентричных секущих сфер)Скачать

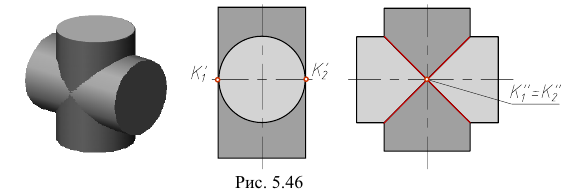
Двойное касание

Все образующие обеих поверхностей пересекаются между собой. Пересекающиеся поверхности имеют две общие касательные плоскости. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точках касания (рис. 5.46).

Пересечение поверхностей второго порядка

В общем случае две поверхности второго порядка пересекаются по пространственной кривой четвертого порядка. Следует отметить, что при некоторых особых положениях относительно друг друга поверхности второго порядка могут пересекаться по плоским кривым второго порядка, то есть пространственная кривая пересечения распадается на две плоские кривые.

Теорема о двойном касании

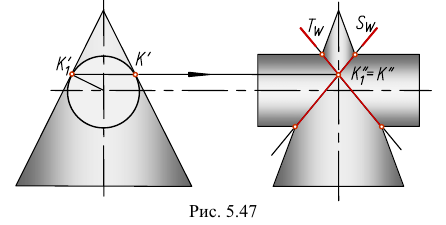
Если две поверхности второго порядка имеют две общие точки (точки касания), то линия их взаимного пересечения распадается на две плоские кривые второго порядка. Причем плоскости этих кривых пройдут через прямую, соединяющую точки касания.

На рис. 5.47 показано построение линии пересечения поверхно­стей прямого кругового цилиндра и эллиптического конуса. Линии пересечения — эллипсы — лежат в профильно-проецирующих плоскостях S и Т, проходящих через прямую соединяющую точки касания.

Теорема Монжа

Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их взаимного пересечения распадается на две плоские кривые. Плоскости этих кривых пройдут через прямую, соединяющую точки пересечения линий касания.

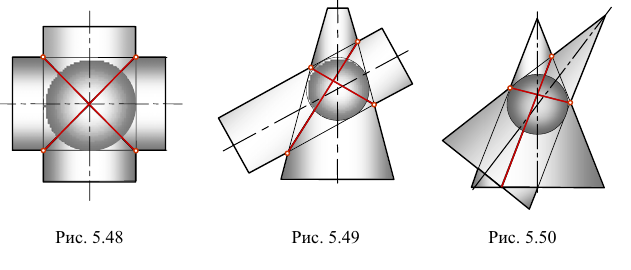
Если оси пересекающихся поверхностей вращения параллельны какой — либо плоскости проекций, то на эту плоскость кривые линии проецируются в прямые.

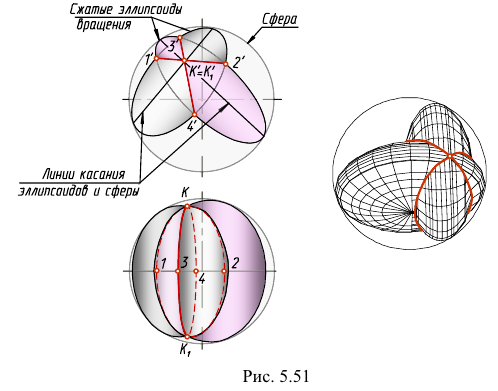
На рис. 5.48 — 5.50 приведены примеры построения линий пересе­чения поверхностей на основании теоремы Монжа, где два цилиндра, цилиндр и конус и два конуса описаны вокруг сферы, а на рис. 5.51 приведен пример построения линии пересечения двух сжатых эллипсоидов вращения, вписанных в сферу.

• Пересечения поверхностей с прямой и плоскостью
• Взаимное пересечение поверхностей
• Собственные тени поверхностей вращения
• Построение падающих теней
• Взаимное положение прямой и плоскости
• Решение метрических задач
• Тени в ортогональных проекциях
• Кривые поверхности

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Урок 8. Построение линии пересечения поверхностей цилиндров

Здравствуйте! На сегодняшнем уроке мы построим линию пересечения поверхностей двух цилиндров.

Исходное задание берем из задачника С. К. Боголюбова, 1989 год, стр. 141, вар. 1.

При выполнении задания воспользуемся безосным способом проецирования, т. е. без обозначения осей координат.

Я предлагаю вам сначала сделать 3d модель пересекающихся цилиндров, а затем, на ассоциативном чертеже построить линию пересечения цилиндров.

Видео:Пересечение поверхностей полусферы и цилиндра. Пошаговое видео. Инженерная графикаСкачать

Создание ассоциативного чертежа пересекающихся цилиндров

1. Сначала на плоскости zx (горизонтальной) вычерчиваем окружность диаметром 80 мм, выдавливаем на 80 мм.

2. Затем на плоскости zy создаем эскиз полуцилиндра радиусом 45 мм.

Выдавливаем эскиз на длину 110 мм, направление выдавливания – средняя плоскость .

3. Создаем чертеж, вставляем стандартные виды и изометрию детали. Щелкнув правой кнопкой мыши по габаритному прямоугольнику, разрушаем связи проекций с моделью. Это нам нужно для того, чтобы перестроить линии пересечения вручную.

4. Удаляем линии пересечения на фронтальной проекции и изометрии. Конечно, можно все оставить и так, Компас построил линию пересечения цилиндров очень точно. Но так как нам нужно показать свои знания, мы перестроим линию вручную.

Как построить линию пересечения цилиндров?

Построение линии пересечения двух цилиндров начинаем с нахождения проекций очевидной точки 4 и характерной точки 1. Делаем это по линиям связи.

Затем на профильной проекции проводим две вспомогательные секущие плоскости Pw и Pw1 произвольно.

Далее находим проекции точек пересечения плоскостей с контуром детали, по линиям связи.

При помощи кривой Безье соединяем полученные точки на фронтальной проекции.

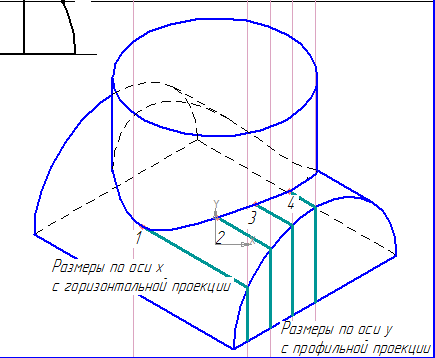
На изометрии точки находятся путем перенесения соответствующих координат точек по осям x и y и соединения их кривой Безье.

Координаты точки 1 находим, проведя вспомогательную прямую через середину нижнего основания модели.

Готовый чертеж с вновь построенной линией пересечения поверхностей цилиндров.

Возможно, вас заинтересует урок по моделированию корпуса водопроводного крана, в нем также реализовано построение линии пересечения поверхностей вращения.

Пример подробно разобран в видеоуроке. Посмотрите его.

Итак, сегодня вы научились строить линию пересечения двух цилиндров на ортогональных проекциях и в изометрии.

Видео:Пересечение двух поверхностей вращения - конуса и цилиндраСкачать

Пересечение поверхностей вращения. Два цилиндра

На рис. 197 приведен случай пересечения двух цилиндров под прямым углом. Горизонтальные проекции линий пересечения совпадают с контуром вертикально расположенного цилиндра. Пересечение фронтальных проекций крайних образующих линий цилиндров определяет точки 1₂, 2₂, 3₂ и 4₂ С помощью горизонтальных проекций 5₁ и 6₁ находят фронтальные проекции 5₂ и 6₂ передних точек линий пересечения. Для нахождения промежуточных точек проводят горизонтальную плоскость ?. Эта плоскость пересечет вертикальный цилиндр по окружности, горизонтальная проекция которой совпадает с контуром этого цилиндра. Горизонтально расположенный цилиндр пересечется с плоскостью ? по образующим, которые удобнее найти с помощью третьей проекции (точки 73, 83). При отсутствии третьей проекции пользуются вспомогательной полуокружностью плоскости П₂. Она позволяет определить расстояние у от образующих до оси цилиндра. Получив горизонтальную проекцию 7₁ находят ее фронтальную проекцию 7₂ на фронтальной проекции ?₂ плоскости-посредника ?. Задачу решают путем проведения ряда таких плоскостей.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284966965_two-cylinders.jpg|—>TEnd—>

Линию пересечения в изометрической проекции строят с помощью одного из оснований цилиндров, в данном случае с помощью левого основания горизонтального цилиндра. От соответствующих точек этого основания по образующим откладывают величины, взятые с фронтальной или горизонтальной проекций цилиндра. Таким путем на чертеже построены точки 7′, 5′ и обведена четвертая часть передней (левой) линии пересечения; другие точки линии пересечения находятся аналогично; задняя (правая) линия пересечения в этом примере будет невидимой.

📸 Видео

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Лекция 13. Пересечение поверхностей метод концентрических сферСкачать

Пересечение поверхностей. Построение линии пересечения.Скачать

Задание 54. Аксонометрия ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 2Скачать

85КБ. Пересечение поверхностей цилиндра и полусферы. Определение видимости.Скачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Построение линии пересечения поверхностей методом СЕКУЩИХ ПЛОСКОСТЕЙСкачать

Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать

Как построить ЛИНИИ ПЕРЕСЕЧЕНИЯ трехгранной ПРИЗМЫ С ЦИЛИНДРОМСкачать

Лекция 12. Пересечение поверхностей метод плоскостейСкачать

Взаимное пересечение поверхностей/ (способ секущих плоскостей)/ Задача 49./ Рабочая тетрадь.Скачать