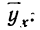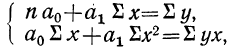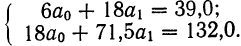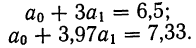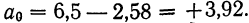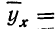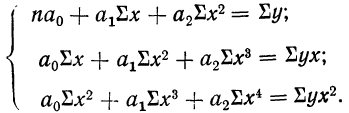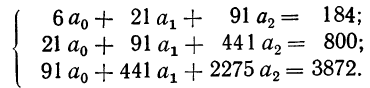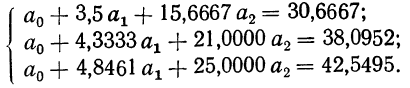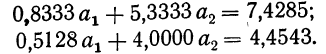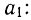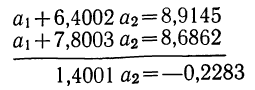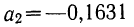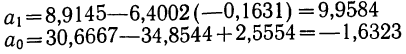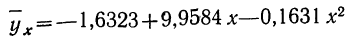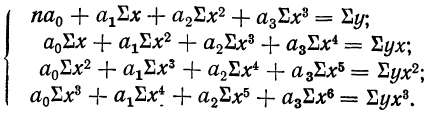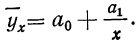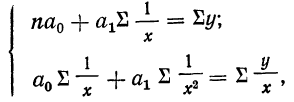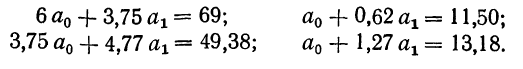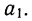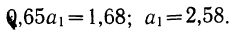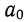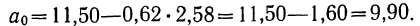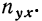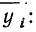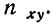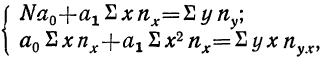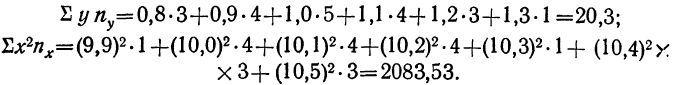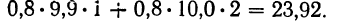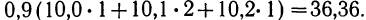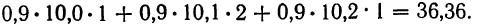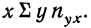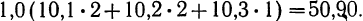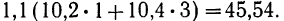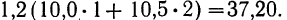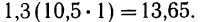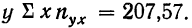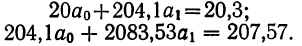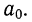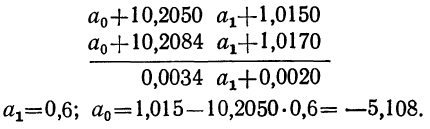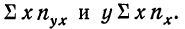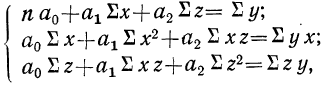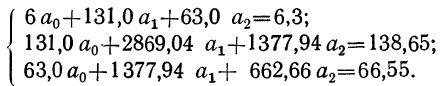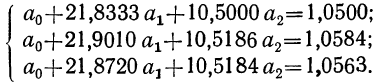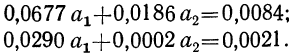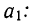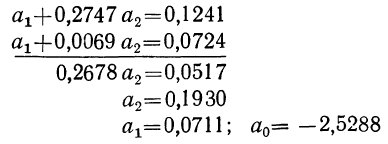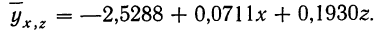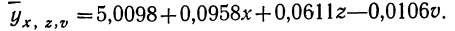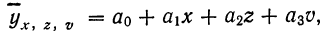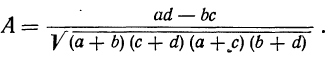Уравнение линейной зависимости смысл коэффициентов

Видео:Математика #1 | Корреляция и регрессияСкачать

Определение параметров линейной зависимости

Если есть основания предполагать, что исследуемая зависимость двух величин Y и X является линейной, то есть удовлетворяет формуле

, (10.1)

и экспериментальный график зависимости y(x) это подтверждает, то есть через доверительные интервалы всех экспериментальных точек можно провести прямую линию, то по результатам измерения величин Y и X, то есть по значениям координат экспериментальных точек, можно определить параметры линейной зависимости k и b. Это можно сделать по крайней мере двумя способами.

Первый способ – графический.

· Надо провести прямую линию на графике так, чтобы она пересекла доверительные интервалы всех точек и при этом как можно ближе прошла ко всем точкам. После этого можно приступить к определению k и b.

· k представляет собой угловой коэффициент прямой, поэтому его можно найти как отношение приращения функции Dy к приращению аргумента Dx. В качестве Dx удобнее всего выбрать разность координат крайних точек графика (x_n – x₁). При этом Dy = y(x_n) – y(x₁).

Графический способ определения параметров прямой линии

Обратите внимание: y(x₁) и y(x_n) – это не ординаты экспериментальных точек y₁ и y_n, физической величины Y, которые получены до построения графика зависимости y(x). Это значения линейной функции y(x), которую изображает проведённая на графике прямая.

· b – это отрезок, который прямая линия графика отсекает на оси ординат (на вертикальной оси), поэтому для нахождения b надо довести экспериментальную прямую до оси ординат и определить ординату их точки пересечения. Но это правило справедливо только в том случае, когда координатные оси пересекаются в начале координат, то есть в точке с координатами (0; 0). Если же удобнее выбрать другую точку пересечения осей, как это сделано при построении графика на рис.5, то нужно использовать другое правило: надо выбрать две точки на прямой, например, точки с координатами (x₁; y(x₁)) и (x_n; y(x_n)) и записать уравнение прямой, проходящей через эти точки:

. (10.2)

Приведение этого уравнение к виду (10.1) даёт следующее выражение для b:

. (10.3)

Описанный метод определения параметров прямой линии k и b есть метод их косвенного измерения. А так как всякое измерение обладает погрешностью, то возникает вопрос: как оценить погрешности D(k) и D(b)? Проще всего это сделать так.

· Надо провести через доверительные интервалы ещё две прямые линии: для первой из них параметры k и b должны быть максимально возможными, поэтому её надо провести как можно круче и выше, для второй – значения k и b должны быть минимально возможными, её надо провести как можно полого и ниже.

· После этого погрешности D(k) и D(b) можно определить очевидным образом:

(10.4)

Второй способ определения параметров линейной зависимости, полученной экспериментальным путём, – аналитический.

Он называется методом наименьших квадратов. Его идея в том, что среди всевозможных комплектов пары чисел k и b существует такой единственный комплект, для которого сумма квадратов отклонений ординат экспериментальных точек от соответствующих ординат прямой линии с параметрами k и b, минимальна. Не рассматривая этот метод в деталях, приведём конечные выражения, позволяющие определить k и b.

(10.2)

(10.3)

В этих формулах n – число экспериментальных точек, а наборы чисел (x_i) и (y_i) – результаты измерений, то есть абсциссы и ординаты экспериментальных точек.

Проделав вычисления по формулам (10.2) – (10.3), следует сделать проверку. Для этого надо по формуле (10.1) вычислить значения ординат прямой линии при двух произвольных значениях x, например при x₁ и при x_n, затем нанести на график две контрольные точки, то есть точки с координатами (x₁, y(x₁)) и (x_n, y(x_n)), и соединить их прямой линией. Если все вычисления проделаны верно, то прямая автоматически пройдёт оптимальным образом, то есть пересечёт доверительные интервалы всех экспериментальных точек и при этом будет максимально приближена к экспериментальным точкам.

Погрешности косвенного измерения параметров прямой линии k и b методом наименьших квадратов определяются по следующим формулам:

(10.4)

. (10.5)

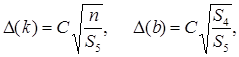
Литература

1. Зайдель А.Н. Погрешности измерений физических величин. -Л.: Наука, 1985. – 110 с.

2. Рабинович С.Г. Погрешности измерений. Л.: Энергия, 1978. -258 с.

[1] Число измерений в серии n называется объёмом серии.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Корреляция — определение и вычисление с примерами решения

Содержание:

Понятие о корреляции:

Марксистская философия учит, что каждое явление природы и общества не возникает само по себе, отдельно от других, а находится в связи с другими явлениями, причем каждое из них представляет собой единство составляющих его частей и свойств. Для того чтобы познать какое-либо явление, необходимо изучить его не только во всех сложных взаимоотношениях с окружающими явлениями-факторами, но также во взаимосвязи всех его сторон.

Если всеобщая связь и взаимозависимость явлений составляют один из наиболее общих законов, то основной задачей науки является изучение этой взаимосвязи.

В математической статистике взаимосвязь явлений изучается методом корреляции. Термин корреляция происходит от английского слова correlation — соотношение, соответствие. Особенность изучения связи явлений методом корреляции состоит в том, что нельзя изолировать влияние посторонних факторов либо потому, что эти факторы неизвестны, либо потому, что их изоляция невозможна. Поэтому метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выяснить, какова была бы зависимость между результатом фактором, если бы посторонние факторы не изменялись и своим изменением не искажали основную зависимость. При этом небольшое число наблюдений не дает возможности обнаружить закономерность связи.

Первая задача корреляции заключается в выявлении на основе наблюдения над большим количеством фактов того, как изменяется в среднем результативный признак в связи с изменением данного фактора. Это изменение предполагает условие неизменности ряда других факторов, хотя искажающее влияние этих других факторов на самом деле имеет место. Вторая задача заключается в определении степени влияния искажающих факторов.

Первая задача решается нахождением уравнения связи.

Вторая задача решается при помощи различных показателей тесноты связи.

Такими показателями являются меры тесноты связи, найденные разными исследователями, а также коэффициент корреляции и корреляционное отношение.

Видео:Парная регрессия: линейная зависимостьСкачать

Результативный и факториальный признаки

При изучении влияния одних признаков явлений на другие из цепи признаков, характеризующих данное явление, выделяются два признака — факториальный и результативный. Необходимо установить, какой из признаков является факториальным и какой результативным. В этом помогает прежде всего логический анализ.

Пример. Себестоимость промышленной продукции отдельного предприятия зависит от многих факторов, в том числе от объема продукции на данном предприятии. Себестоимость продукции выступает в этом случае как результативный признак, а объем продукции — как факториальный.

Другой пример. Чтобы судить о преимуществах крупных предприятий перед мелкими, рассмотрим, как увеличивается производительность труда рабочих крупных предприятий, и выявим зависимость производительности труда от увеличения размеров предприятия.

Таблица!

Группировка магазинов Министерства торговли по числу рабочих мест на 1 января 1960 г.1

Группы магазинов по числу рабочих мест Число магазинов Товарооборот в расчете на одного работника за квартал (в тыс. руб.)

Всего 68 375 117

Из них

с числом рабочих мест:

• с 1 19 893 109
• с 2 18 030 108
• с 3—4 16 508 108
• с 5—7 8 321 111
• с 8—10 2 868 118
• с 11 — 15 1 559 122
• с 16 и более 1 196 139
• J

Группировка показывает прямую зависимость производительности труда торговых работников, выражающуюся в товарообороте, приходящегося на одного работника, от размера магазина. Признак группировки — число рабочих мест — является факториальным, товарооборот — результативным признаком.

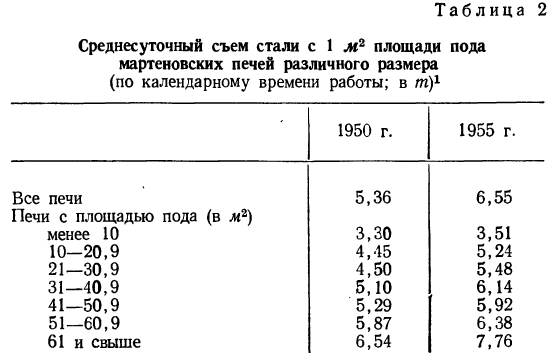
От размеров производства зависит также производительность оборудования, о чем свидетельствует следующая таблица:

Из таблицы ясно видна связь между размерами печей и их производительностью. Эта связь прямая: чем крупнее печь, тем она производительнее.

Однако зависимость результативного признака (суточного съема стали) от факториального носит не обязательный характер. Если в общей массе мы наблюдаем эту связь, то в отдельных группах бывают и отступления от общей закономерности. Такие отступления—характерная особенность статистической связи вообще, о которой будет рассказано ниже.

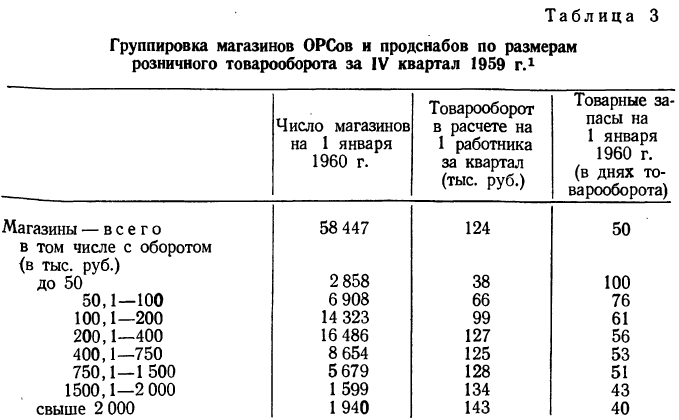
Группировки позволяют выявить и зависимость нескольких результативных признаков от одного факториального. Рассмотрим табл. 3.

В этой таблице мы видим зависимость двух результативных признаков: товарооборота на одного работника и товарных запасов—от размеров магазинов. Зависимость товарооборота от размеров магазина прямая, а зависимость товарных остатков от размеров магазина — обратная. В первом случае она растет с ростом размеров магазина, во втором уменьшается. Однако то и другое благоприятно.

Графическое изображение связи

Графическое изображение изучаемых явлений позволяет не только установить наличие или отсутствие связи между ними, но и изучить характер этой связи, иначе говоря изучить форму связи и ее тесноту.

Имея перед собой числовые характеристики факториального и результативного признаков одного и того же явления, можно каждую пару чисел изобразить в виде точки на плоскости. Для этого на плоскости берем две взаимно перпендикулярные линии и образуем систему координат. В этой системе по оси абсцисс откладываем значения факториального признака, а по оси ординат— значения результативного признака. Каждая пара чисел дает при этом точку на плоскости координатного поля.

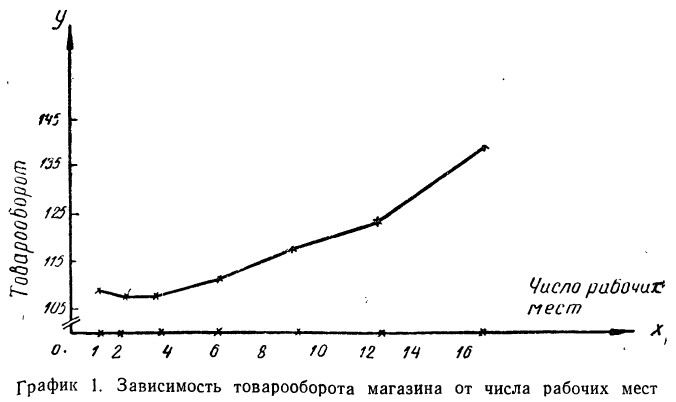
Возьмем, например, группировку магазинов по числу рабочих мест, данную на стр. 239, и будем откладывать число рабочих мест по горизонтальной оси (оси Ох), а товарооборот в расчете на одного работника — по вертикальной оси (оси Оу). Будем иметь ряд точек, соединив которые получим ломаную линию, которая называется ломаной регрессии (см. график 1).

Как видно из графика, с ростом числа рабочих мест в магазине растет и товарооборот, приходящийся на одного работника, что говорит о связи между этими признаками, причем связи прямой. График подчеркивает эту зависимость ходом ломаной линии из нижнего угла в верхний правый угол.

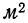
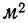
Такого же рода зависимость будем наблюдать на графике 2, изучая связь между величиной мартеновских печей по площади пода и среднесуточным съемом стали с 1 пода. Как и в предыдущем примере, факториальный признак — величину площади пода — будем откладывать на оси абсцисс, а результативный — среднесуточный съем стали с 1 пода — на оси ординат.

Здесь также ясно выраженная прямая зависимость между результативным и факториальным признаками.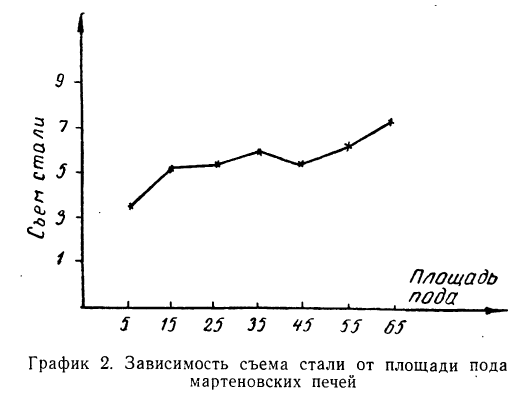

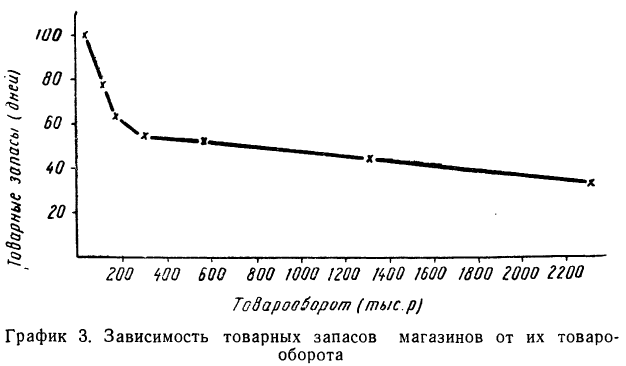
По-другому будет выглядеть график зависимости товарных запасов от размера товарооборота магазина.

Здесь мы наблюдаем ярко выраженную обратную связь между признаками: падение товарных запасов сопровождается ростом размера магазина по товарообороту.

Графический метод наглядно иллюстрирует зависимость, выявленную группировкой. Недостаток графического метода изучения связи заключается в том, что он позволяет выявить связь лишь между двумя признаками.

Функциональные и статистические связи

До сих пор говорилось о связях между явлениями и их признаками без объяснения формы и степени этих связей. В приведенных примерах связи носят логически обоснованный характер, но числовое выражение этих связей говорит о том, что они проявляются не всегда одинаково. В определенных случаях имеются отступления от наблюдаемых общих закономерностей. В приведенной на стр. 240 таблице о среднесуточном съеме стали с 1 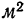пода печи наблюдается зависимость съема стали от размера печи по площади пода, но эта зависимость за 1955 г. искажена показателями 5-й группы, где съем стали значительно ниже, чем в 4-й группе. Если бы рассматривалась при этом каждая печь в отдельности, то это несоответствие установленному правилу зависимости проявлялось бы неоднократно. Но средние величины съема стали, вычисленные на основании данных довольно большого числа печей в группе, говорят о явно выраженной зависимости. Связи между явлениями, или их признаками. проявляющиеся в изменении в зависимости от одного признака характеристик распределения (из которых главная — средняя) другого признака, называются связями статистическими.

Статистические связи характеризуются тем, что в них результативный признак не полностью определяется влиянием признака факториального. Это влияние проявляется лишь в среднем, а в отдельных случаях получаются результаты, даже противоречащие установленной связи.

В отличие от статистических связей связи функциональные характеризуются тем, что при таких связях факториальный признак полностью определяет величину результативного признака.

Функциональные связи почти не встречаются в явлениях общественной жизни, отличающихся сложностью и многообразием существующих и проявляющихся взаимосвязей. Но во многих явлениях в основе статистических связей лежат функциональные связи. Связь функциональная может показывать зависимость между результативным признаком и несколькими аргументами. Так, площадь прямоугольника зависит от длины его двух сторон, путь, проходимый телом, зависит от скорости его движения и времени движения и т. д.

Уравнение связи

Наблюдая статистическую связь между двумя признаками, математическая статистика стремится придать этой связи форму функциональной, т. е. связи, выражаемой при помощи математической функции.

На помощь приходит ее графическое изображение при отыскании нужной функции связи. При этом необходимо стремиться найти такую функцию, которая давала бы наименьшее отклонение от полученных при наблюдении значений их признаков, которая выражала бы основную зависимость, проявляющуюся в эмпирическом материале. Уравнение этой функции будет уравнением связи между результативным и факториальным признаками.

Уравнение связи находится с помощью способа наименьших квадратов, который требует, чтобы сумма квадратов отклонений эмпирических значений от значений, получаемых на основании уравнения связи, была минимальной.

Применение способа наименьших квадратов позволяет находить параметры уравнения связи при помощи решения системы так называемых нормальных уравнений, различных для связи каждого вида.

Чтобы отметить, что зависимость между двумя признаками выражается в среднем, значения результативного признака, найденные по уравнению связи, обозначаются

Зная уравнение связи, можно вычислить заранее среднее значение результативного признака, когда значение факториального признака известно. Таким образом, уравнение связи является методом обобщения наблюдаемых статистических связей, методом их изучения.

Применение той или иной функции в качестве уравнения связи разграничивает связи по их форме: линейную связь и криволинейную связь (параболическую, гиперболическую и др.).

Рассмотрим уравнения связи для зависимостей от одного признака при разных формах связи (линейной, криволинейной параболической, гиперболической) и для множественной связи.

Линейная зависимость

Уравнение связи как уравнение прямой 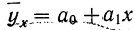применяется в случае равномерного нарастания результативного признака с увеличением признака факториального. Такая зависимость будет зависимостью линейной (прямолинейной).

Параметры уравнения прямой линии 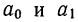находятся путем решения системы нормальных уравнений, получаемых по способу наименьших квадратов:

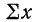
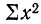
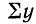
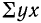
где n — число полученных при наблюдении пар взаимосвязанных величин; — сумма значений факториального признака;

— сумма квадратов значений факториального признака;

— сумма значений результативного признака; — сумма произведений значений факториального признака на значения результативного признака.

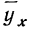
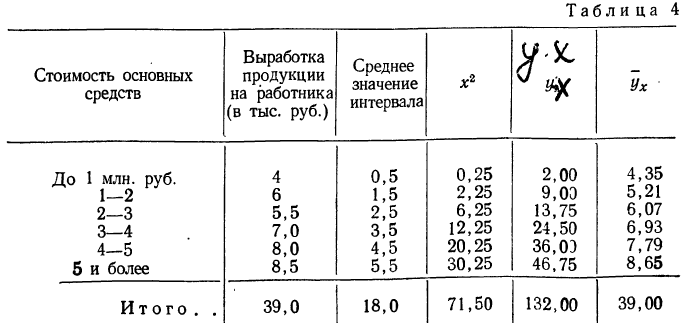
Примером расчета параметров уравнения и средних значений результативного признака может служить следующая таблица, являющаяся результатом группировки по факториальному признаку и подсчета средних по результативному признаку.

Группировка предприятий по стоимости основных средств и подсчет сумм необходимы для уравнения связи.

Из таблицы находим: 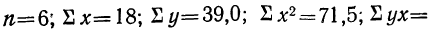132,0. Строим систему двух уравнений с двумя неизвестными:

Поделив каждый член в обоих уравнениях на коэффициенты при 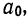получим:

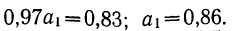
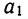
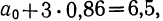
Вычтем из второго уравнения первое: Подставив значения в первое уравнение найдем

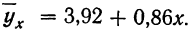
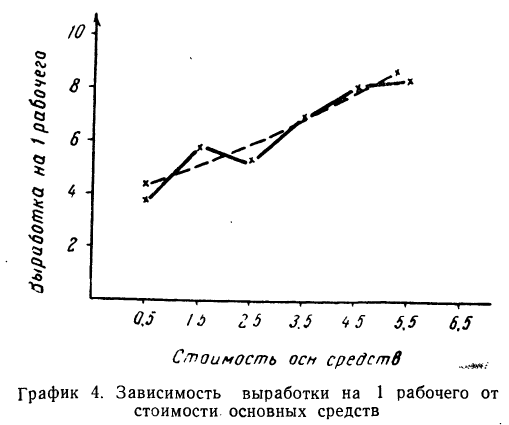
Уравнение связи примет вид: Подставив в это уравнение соответствующие х, получим значения результативного признака, отражающие среднюю зависимость у от х в виде корреляционной зависимости.

Заметим, что суммы, исчисленные по уравнению и фактические, равны между собой. Изображение фактических и вычисленных значений на графике 4 показывает, что уравнение связи отображает наблюденную зависимость в среднем.

Параболическая зависимость

Параболическая зависимость, выражаемая уравнением параболы 2-го порядка 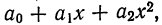имеет место при ускоренном возрастании или убывании результативного признака в сочетании с равномерным возрастанием факториального признака.

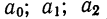
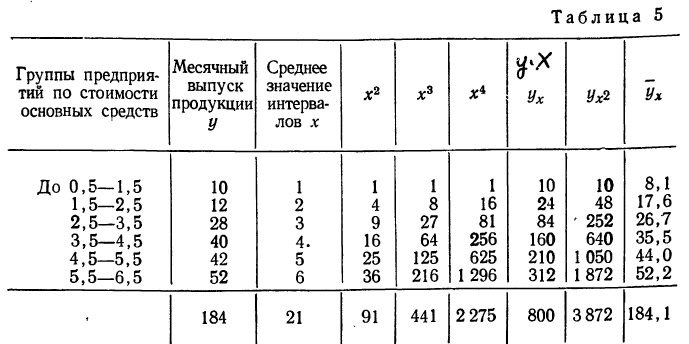
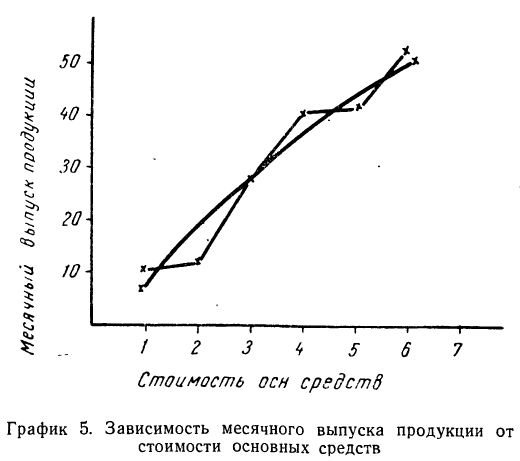
Параметры уравнения параболы вычисляются путем решения системы 3 нормальных уравнений:

Возьмем для примера зависимость месячного выпуска продукции (у) от величины стоимости основных средств (х). Оба показателя округлены до миллионов рублей. Расчеты необходимых сумм приведем в таблице 5.

По данным таблицы, составляем систему уравнений:

После деления всех уравнений на коэффициенты при 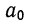получим:

Вычтя из второго уравнения первое и из третьего второе, получим два новых уравнения с двумя неизвестными:

Полученные уравнения снова разделим на коэффициенты при

Следовательно,

Запишем уравнение параболы, выражающей связь между х и у.

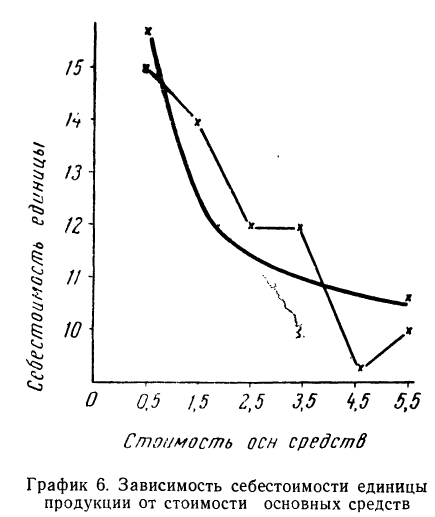
Графическое сопоставление опытных данных и данных расчета (см. график 5) показывает почти полное совпадение хода обеих линий, что говорит о хорошем воспроизведении опытных данных расчетными средними значениями результативного признака.

В практике изучения связи между признаками, кроме параболы 2-го порядка, применяются параболы и более высоких порядков. Чем выше порядок параболы, тем точнее он воспроизводит опытные данные.

Если уравнение связи представляет собой параболу 3-го порядка 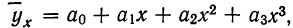то система нормальных уравнений примет вид:

Имея соответствующие хну, можем составить Дополнительную расчетную таблицу по следующей схеме:

которая используется для нахождения нужных сумм. Решив систему 4 уравнений, найдем параметры 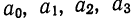и, следовательно, уравнение связи.

Уравнение гиперболы

Обратная связь указывает на убывание результативного признака при возрастании факториального. Такова линейная связь при отрицательном значении 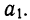В ряде других случаев обратная связь может быть выражена уравнением гиперболы

Параметры уравнения гиперболы 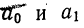находятся из системы нормальных уравнений:

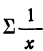
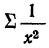
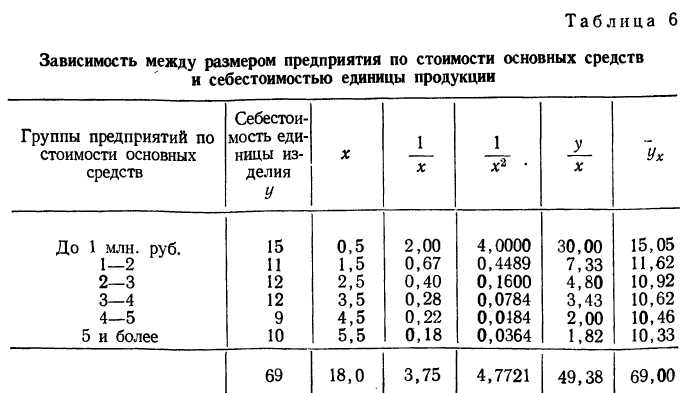
где — сумма величин, обратных значениям факториального признака, а — сумма их квадратов.

Примером расчета обратной связи по гиперболе может служить следующая таблица:

Составив по данным таблицы систему уравнений и разделив каждый член обоих уравнений на коэффициенты при а, получим:

Находим вычитанием из второго уравнения первого величину

Подставив вместо 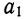его значение, получим

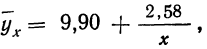
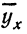
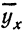
Запишем уравнение связи в общем виде затем, подставив каждое значение х в уравнение, находим по любой строке таблицы. Строим ломаную по парам х и у и кривую по х и . Ломаная и кривая очень близки друг к другу.

Корреляционная таблица

При большом объеме наблюдений, когда число взаимосвязанных пар велико, парные данные легко могут быть расположены в корреляционной таблице, являющейся наиболее удобной формой представления значительного количества пар чисел.

В корреляционной таблице один признак располагается в строках, а другой — в колонка таблицы. Число, расположенное в клетке на пересечении графы и колонки, показывает, как часто встречается данное значение результативного признака в сочетании с данным значением факториального признака.

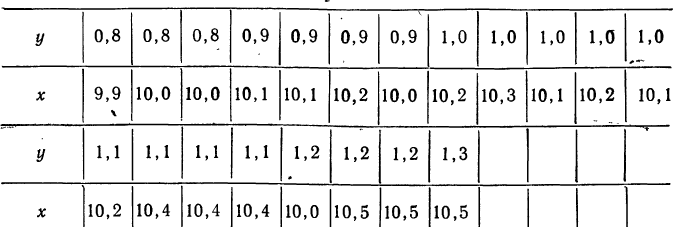
Для простоты расчета возьмем небольшое число наблюдений на 20 предприятиях за средней месячной выработкой продукции на одного рабочего (тыс. руб. — у) и за стоимостью основных производственных средств (млн. руб. — х).

В обычной парной таблице эти сведения располагаются так:

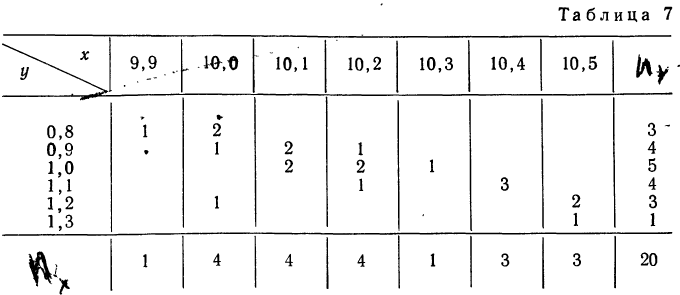
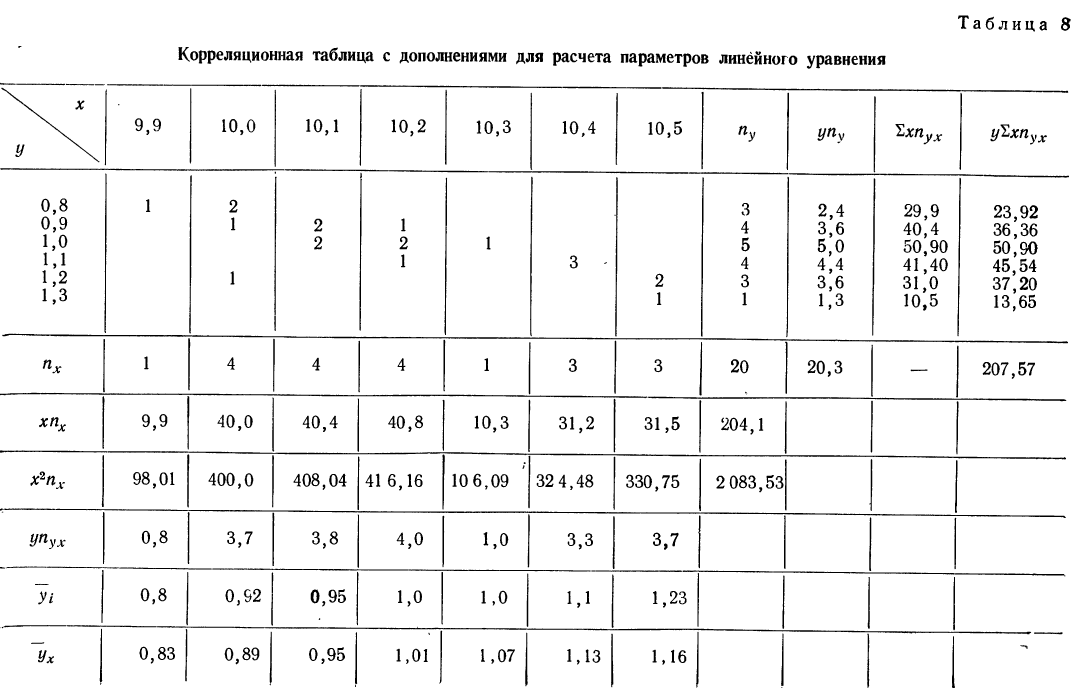
Сведем эти данные в корреляционную таблицу.

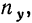
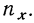
Итоги строк у показывают частоту признака итоги граф х — частоту признака Числа, стоящие в клетках корреляционной таблицы, являются частотами, относящимися к обоим признакам и обозначаются

Корреляционная таблица даже при поверхностном знакомстве дает общее представление о прямой и обратной связи. Если частоты расположены по диагонали вниз направо, то связь между признаками прямая (при увеличивающихся значениях признака в строках и графах). Если же частоты расположены по диагонали вверх направо, то связь обратная.

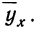
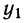
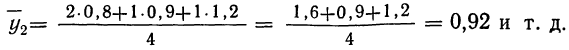
Для предварительного суждения о связи по корреляционной таблице можно для каждого столбца рассчитать средние значения Так, в первом столбце х = 9,9, а имеет лишь одно значение, равное 0,8. Найдем среднее значение для второго столбца. Оно будет равно:

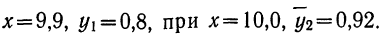
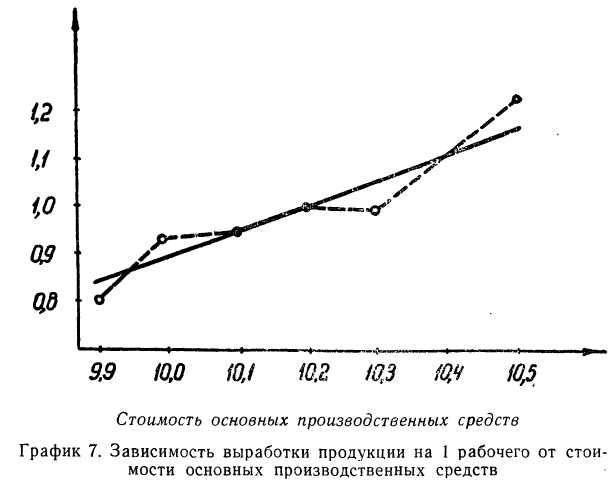
Следовательно, при Выпишем все значения х и соответствующие им

Зависимость, выраженная в таблице, более ярко и убедительно выступит в «ломаной регрессии», когда каждую пару чисел нанесем на график (см. график 7).

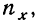
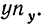
По корреляционной таблице можно вести расчеты параметров уравнения связи, как уравнения прямой, так и уравнений параболы и гиперболы. При этом необходимо учитывать, что сочетание каждой пары значений может встречаться не один, а несколько раз. Сами значения хну необходимо взвешивать, т. е. умножать на соответствующие частоты. Для самого признака х частота будет обозначаться для признака Частоту сочетаний обозначим

Ввиду сказанного мы можем систему нормальных уравнений написать так, чтобы были учтены веса. Тогда для линейной зависимости система нормальных уравнений примет вид:

где N — число произведенных наблюдений (число пар). В приведенной корреляционной таблице N = 20. 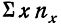будет суммой произведений соответствующих х на их частоты. В данной таблице эта сумма составит:

9,9 +10,0 • 4 +10,1 • 4 + 10,2 • 4 +10,3 • 1 +10,4 • 3 +10,5 • 3 = 204.

—сумма произведений у на соответствующие частоты. В нашем примере она равна:

включает сумму произведений всех х на у и на для тех клеток корреляционной таблицы, в которых записаны частоты. Рассчитаем суммы произведений для 1-й и 2-й строки

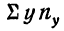
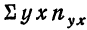
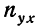
• Для 1 -и строки:
• Для 2-й строки:

Нетрудно заметить, что в каждой строке у повторяется столько раз, сколько раз мы его суммируем, а, следовательно, у можно вынести за скобку.

• Для 1-й строки: 0,8 (9,9 • 1 +10,0 • 2) =23,92.
• Для 2-й строки:

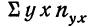
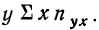
Следовательно, сумма произведений может быть записана при постоянном у, как Заметим, что сумма произведений может быть записана и рассчитана как произведение

Продолжим расчет для последующих строк.

• Для 3-й строки
• Для 4-й строки
• Для 5-й строки
• Для 6-й строки

Общая сумма по всем строкам

Система нормальных уравнений может быть записана по результатам подсчета в таком виде:

Для расчета параметров уравнения линейной связи делим каждое из уравнений на коэффициенты при

Уравнение связи 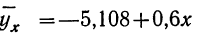определяет среднюю зависимость выработки рабочего от стоимости основных средств. Вычислительная работа облегчается, если в самой корреляционной таблице путем записи дополнительных граф и строк производить нужные подсчеты для решения системы уравнений.

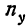
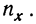
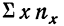
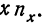
Число наблюдений N может быть подсчитано и по столбцу как его сумма. Она равна итогу по строке Для определения необходимо ввести новую строку Итог этой строки и дает искомую сумму.

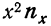
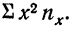
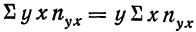
Следующая дополнительная строка представляет возможность определить Далее, и может быть определена на основе расчета двух дополнительных граф:

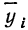
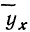
В корреляционной таблице (см. табл. 8) в последних строках дается расчет для построения ломаной регрессии — для построения прямой (см. график 7).

Корреляционная таблица позволяет вычислять уравнение связи для любой формы: прямой, параболы, гиперболы и др. Однако в подобной таблице видна зависимость результативного признака лишь от одного факториального.

Зависимость результативного признака от двух или более факториальных признаков носит название множественной связи.

Множественная связь

Исследование зависимости результативного признака от двух или нескольких факториальных признаков возможно при помощи уравнения множественной связи.

В простейшем уравнении множественной связи предполагается, что зависимость между признаками линейная. Сначала рассмотрим линейную зависимость результативного признака (у) от двух факториальных (х, z). Уравнение связи в этом случае выразится формулой 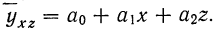Параметры этого уравнения находятся при решении системы нормальных уравнений, получаемых для способа наименьших квадратов

где п — число одновременных наблюдений по трем признакам;

—суммы соответствующих значений по этим признакам.

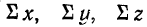
Все расчеты удобно сосредоточить в специальной таблице, как это делается в приводимом ниже примере.

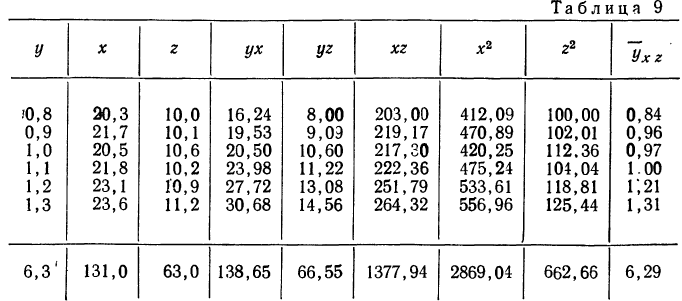
Рассмотрим зависимость средней урожайности ячменя (у) на равных участках от количества внесенных минеральных удобрений (х) и количества выпавших в период цветения осадков (z).

Средняя урожайность исчислялась по участкам с равным количеством внесенных удобрений и с равным количеством выпавших осадков.

Пользуясь данными таблицы, составляем систему трех уравнений:

Поделив все члены уравнений на коэффициенты при 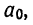получим:

Вычитая из второго уравнения сначала первое, а затем третье, получим 2 уравнения с двумя неизвестными:

Делим каждый член обоих уравнений на коэффициенты при

Уравнение связи, определяющее зависимость результативного признака (у) от двух факториальных

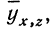
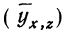
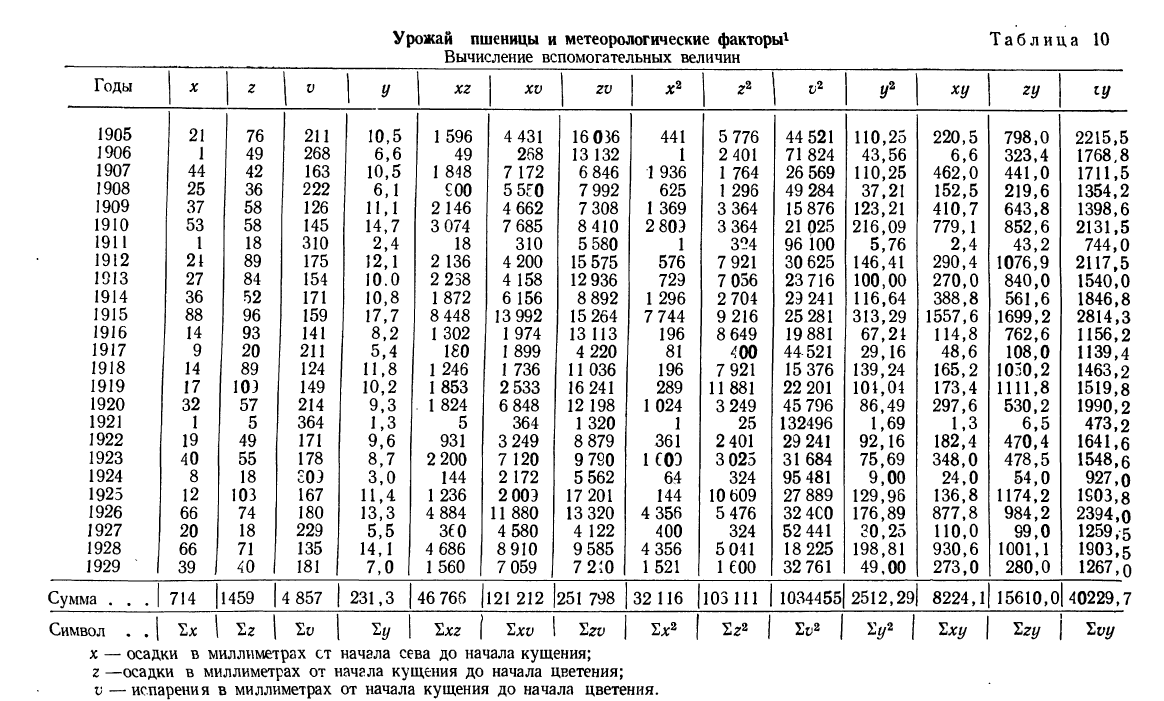
Вычислив по этому уравнению при соответствующих х и z величины замечаем, что суммы опытных данных (y) и расчетных данных совпадают, а отдельные значения их мало отличаются друг от друга.

Найдем уравнение связи между урожайностью пшеницы на Безенчукской опытной станции и тремя факторами (х, z, v).

Статистические данные, полученные в результате наблюдения, и расчеты представлены в табл. 10, откуда возьмем необходимые данные для составления системы нормальных уравнений:

Следовательно,, корреляционное уравнение будет:

Расширив число факториальных признаков, можно найти уравнение множественной связи для 4, 5, 6 и т. д. признаков. При этом необходимо брать только такие признаки, которые оказывают существенное влияние на величину результативного признака, ибо учет несущественных, второстепенных признаков лишь увеличивает расчетную работу при нахождении уравнения связи, а не приближает к более полному изучению связи.

Если число факториальных признаков возрастает, возрастает и число членов уравнения связи. Так, для трех факториальных признаков линейное уравнение связи будет записано формулой:

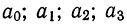
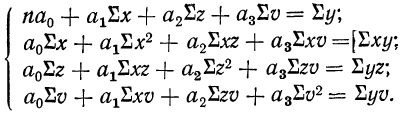
где параметры уравнения находятся путем решения системы четырех нормальных уравнений:

Построив соответствующую таблицу, получим в ней необходимые суммарные данные для приведенной системы уравнений (см. табл. 10).

Мерой существенности влияния того или иного факториального признака на результативный являются показатели тесноты связи.

В настоящем издании мы рассмотрим эмпирические меры тесноты связи, полученные разными исследователями, и меры тесноты связи, основанные на измерении вариации.

Эмпирические меры тесноты связи

Эмпирические меры тесноты связи позволяют оценить степень связи между явлениями или факторами, находящимися в зависимости один от другого. Эмпирические меры получены различными исследователями, занимавшимися статистической обработкой фактического материала. Они получены ранее, чем был открыт метод корреляции. Практическое пользование эмпирическими показателями довольно удобно.

К эмпирическим мерам тесноты относятся:

• а) коэффициент ассоциации:
• б) коэффициенты взаимной напряженности;
• в) коэффициент Фехнера;
• Г) коэффициент корреляции рангов;

Рассмотрим каждый из них.

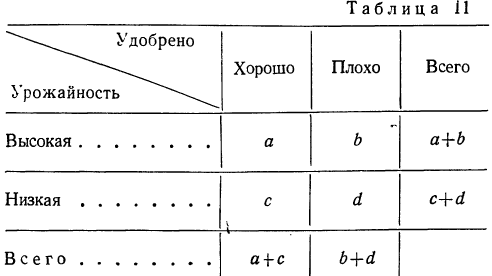
а) Коэффициент ассоциации. Коэффициент ассоциации как мера тесноты связи применяется для изучения связи двух качественных признаков, состоящих только из двух групп. Для его вычисления строится четырехклеточная таблица корреляции, которая выражает связь между двумя явлениями, каждое из которых, в свою очередь, должно быть альтернативным, т. е. состоящим только из двух видов, качественно отличных друг от друга. Например, при изучении зависимости урожая от количества внесенных в почву удобрений выделяем по урожайности и по количеству внесенных удобрений лишь по две группы. При этом условии можно построить следующую четырехклеточную таблицу.

Числа, стоящие на пересечении строк и граф — a,b,c,d, показывают, сколько участков встречается с тем и другим количеством удобрений, внесенным в почву, с той и другой урожайностью.

Мера тесноты связи — коэффициент ассоциации — исчисляется по формуле:

Заполнив клетки конкретными числовыми данными, получим следующую четырехклеточную таблицу, где числа, стоящие в клетках, — гектары посевов.

Коэффициент ассоциации равен: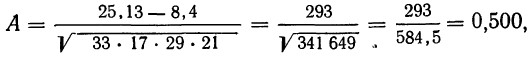
что говорит о достаточно тесной прямой связи между урожайностью и степенью удобрения почв.

Коэффициент ассоциации может иметь и отрицательные значения, когда ad

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Корреляция и регрессия

Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.

Для наших данных система уравнений имеет вид:

10a + 356b = 49
356a + 2135b = 9485

Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17

Уравнение регрессии:
y = 68.16 x — 11.17

1. Параметры уравнения регрессии.
Выборочные средние.

1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.

1.2. Уравнение регрессии (оценка уравнения регрессии).

Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.

1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:

Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.

1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.

1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.

2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим t_крит:
t_крит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 _r = t 2 _b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:

S 2 _y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
S_y = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S _a — стандартное отклонение случайной величины a.

S_b — стандартное отклонение случайной величины b.

2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bx_p ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X _p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx _i ± ε)
где

С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит = (7;0.05) = 1.895

Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — t_крит S_b; b + t_крит S_b)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — t_a)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).

Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.

Обнаружение автокорреляции

1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения e_i с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения e_i (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости e_i от e_i-1.

📺 Видео

Линейная зависимость векторовСкачать

Линейная зависимость и линейная независимость. ТемаСкачать

Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Коэффициент линейной регрессии, 2 способаСкачать

Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Задание 5 Знаки коэффициентов k и b в формуле линейной функции y=kx+bСкачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

Линейная зависимость векторов на примерахСкачать

Эконометрика. Линейная парная регрессияСкачать

7 класс - Алгебра - Определение углового коэффициентаСкачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Коэффициент детерминации. Основы эконометрикиСкачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Лекция 8. Линейная регрессияСкачать

Расчет коэффициента корреляции в ExcelСкачать

Эконометрика Линейная регрессия и корреляцияСкачать