Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования зависимостей между социально-экономическими переменными. Эту задачу мы рассмотрим в рамках самой распространенной в статистических пакетах классической модели линейной регрессии.
Специфика социологических исследований состоит в том, что очень часто необходимо изучать и предсказывать социальные события. Вторая часть данной главы будет посвящена логистической регрессии, целью которой является построение моделей, предсказывающих вероятности событий.
Линейная модель связывает значения зависимой переменной Y со значениями независимых показателей X k (факторов) формулой:
Y=B 0 +B 1 X 1 +:+B p X p + e
где e — случайная ошибка. Здесь X k означает не «икс в степени k «, а переменная X с индексом k .
Традиционные названия «зависимая» для Y и «независимые» для X k отражают не столько статистический смысл зависимости, сколько их содержательную интерпретацию.
Величина e называется ошибкой регрессии. Первые математические результаты, связанные с регрессионным анализом, сделаны в предположении, что регрессионная ошибка распределена нормально с параметрами N(0,? 2 ) , ошибка для различных объектов считаются независимыми. Кроме того, в данной модели мы рассматриваем переменные X как неслучайные значения, Такое, на практике, получается, когда идет активный эксперимент, в котором задают значения X (например, назначили зарплату работнику), а затем измеряют Y (оценили, какой стала производительность труда). За это иногда зависимую переменную называют откликом. Теория регрессионных уравнений со случайными независимыми переменными сложнее, но известно, что, при большом числе наблюдений, использование метода разработанного для неслучайных X корректно.
Благодаря полученным оценкам коэффициентов уравнения регрессии могут быть оценены прогнозные значения зависимой переменной , причем они могут быть вычислены и там, где значения y определены, и там где они не определены. Прогнозные значения являются оценками средних, ожидаемых по модели значений Y , зависящих от X .
Поскольку коэффициенты регрессии — случайные величины, линия регрессии также случайна. Поэтому прогнозные значения случайны и имеют некоторое стандартное отклонение , зависящее от X . Благодаря этому можно получить и доверительные границы для прогнозных значений регрессии (средних значений y ).
Кроме того, с учетом дисперсии остатка могут быть вычислены доверительные границы значений Y (не средних, а индивидуальных!).
Для каждого объекта может быть вычислен остаток e i = 
Для изучения отклонений от модели удобно использовать стандартизованный остаток — деленный на стандартную ошибку регрессии.
Случайность оценки прогнозных значений Y вносит дополнительную дисперсию в регрессионный остаток, из-за этого дисперсия остатка зависит от значений независимых переменных ( 

Таким образом, мы можем получить: оценку (прогнозную) значений зависимой переменной Unstandardized predicted value), ее стандартное отклонение (S.E. of mean predictions), доверительные интервалы для среднего Y(X) и для Y(X) (Prediction intervals — Mean, Individual).
Это далеко не полный перечень переменных, порождаемых SPSS.
Пусть прогнозируется вес ребенка в зависимости от его возраста. Ясно, что дисперсия веса для четырехлетнего младенца будет значительно меньше, чем дисперсия веса 14-летнего юноши. Таким образом, дисперсия остатка e i зависит от значений X , а значит условия для оценки регрессионной зависимости не выполнены. Проблема неоднородности дисперсии в регрессионном анализе называется проблемой гетероскедастичности.
В SPSS имеется возможность корректно сделать соответствующие оценки за счет приписывания весов слагаемым минимизируемой суммы квадратов. Эта весовая функция должна быть равна 1/? 2 (x) , где ? 2 (x) — дисперсия y как функция от x . Естественно, чем меньше дисперсия остатка на объекте, тем больший вес он будет иметь. В качестве такой функции можно использовать ее оценку, полученную при фиксированных значениях X .
Например, в приведенном примере на достаточно больших данных можно оценить дисперсию для каждой возрастной группы и вычислить необходимую весовую переменную. Увеличение влияния возрастных групп с меньшим возрастом в данном случае вполне оправдано.
В диалоговом окне назначение весовой переменной производится с помощью кнопки WLS (Weighed Least Squares — метод взвешенных наименьших квадратов).
В меню — это команда Linear Regression. В диалоговом окне команды:
— Назначаются независимые и зависимая переменные,
— Назначается метод отбора переменных. STEPWISE — пошаговое включение/удаление переменных. FORWARD — пошаговое включение переменных. BACKWARD — пошаговое исключение переменных. При пошаговом алгоритме назначаются значимости включения и исключения переменных (OPTIONS). ENTER — принудительное включение.
— Имеется возможность отбора данных, на которых будет оценена модель (Selection). Для остальных данных могут быть оценены прогнозные значения функции регрессии, его стандартные отклонения и др.
— Назначения вывода статистик (Statistics) — доверительные коэффициенты коэффициентов регресии, их ковариационная матрица, статистики Дарбина-Уотсона и пр.
— Задаются графики рассеяния остатков, их гистограммы (Plots)
— Назначаются сохранение переменных(Save), порождаемых регрессией.
— Если используется пошаговая регрессия, назначаются пороговые значимости для включения (PIN) и исключения (POUT) переменных (Options).
— Если обнаружена гетероскедастичность, назначается и весовая переменная.
Обычно демонстрацию модели начинают с простейшего примера, и такие примеры Вы можете найти в Руководстве по применению SPSS. Мы пойдем немного дальше и покажем, как получить полиномиальную регрессию.
Курильский опрос касался населения трудоспособного возраста. Как показали расчеты, в среднем меньшие доходы имеют молодые люди и люди старшего возраста. Поэтому, прогнозировать доход лучше квадратичной кривой, а не простой линейной зависимостью. В рамках линейной модели это можно сделать, введя переменную — квадрат возраста. Приведенное ниже задание SPSS предназначено для прогноза логарифма промедианного дохода (ранее сформированного).
REGRESSION /DEPENDENT lnv14m /METHOD=ENTER v9 v9_2
/SAVE PRED MCIN ICIN.
*регрессия с сохранением предсказанных значений и доверительных интервалов средних и индивидуальных прогнозных значений.
Таблица 5.1 показывает, что уравнение объясняет всего 4.5% дисперсии зависимой переменной (коэффициент детерминации R 2 =.045), скорректированная величина коэффициента равна 0.042, а коэффициент множественной корреляции равен 0.211. Много это или мало, трудно сказать, поскольку у нас нет подобных результатов на других данных, но то, что здесь есть взаимосвязь, можно понять, рассматривая таблицу 6.2.
Таблица 6.1. Общие характеристики уравнения
Adjusted R Square
Std. Error of the Estimate
a Predictors: (Constant), V9_2, V9 Возраст
b Dependent Variable: LNV14M логарифм промедианного дохода
Результаты дисперсионного анализа уравнения регрессии показывает, что гипотеза равенства всех коэффициентов регрессии нулю должна быть отклонена.
Таблица 6.2. Дисперсионный анализ уравнения
Видео:STAT 7 Регрессия SPSSСкачать

Простая линейная регрессия
16.1 Простая линейная регрессия
Чтобы вызвать регрессионный анализ в SPSS, выберите в меню Analyze. (Анализ) ► Regression. (Регрессия). Откроется соответствующее подменю.
Рис. 16.1: Вспомогательное меню Regression (Регрессия)
При изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных). Никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.
Этот вид регрессии лучше всего подходит для того, чтобы продемонстрировать основополагающие принципы регрессионного анализа. Рассмотрим пример из раздела корреляционный анализ с зависимостью показателя холестерина спустя один месяц после начала лечения от исходного показателя. Можно легко заметить очевидную связь: обе переменные развиваются в одном направлении и множество точек, соответствующих наблюдаемым значениям показателей, явно концентрируется (за некоторыми исключениями) вблизи прямой (прямой регрессии). В таком случае говорят о линейной связи.
у = b • х + а,
где b — регрессионные коэффициенты, a — смещение по оси ординат (OY).
Смещение по оси ординат соответствует точке на оси Y (вертикальной оси), где прямая регрессии пересекает эту ось. Коэффициент регрессии b через соотношение:
b = tg(a) — указывает на угол наклона прямой.
При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая, для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.
Если мы рассмотрим показатель холестерина через один месяц (переменная chol1) как зависимую переменную (у), а исходную величину как независимую переменную (х), то тогда для проведения регрессионного анализа нужно будет определить параметры соотношения:
chol1 = b • chol0 + a
После определения этих параметров, зная исходный показатель холестерина, можно спрогнозировать показатель, который будет через один месяц.
Расчёт уравнения регрессии
Выберите в меню Analyze. (Анализ) ► Regression. (Регрессия) ► Linear. (Линейная). Появится диалоговое окно Linear Regression (Линейная регрессия).
Перенесите переменную chol1 в поле для зависимых переменных и присвойте переменной chol0 статус независимой переменной.
Ничего больше не меняя, начните расчёт нажатием ОК.
Рис.16.2: Диалоговое окно Линейная регрессия
Вывод основных результатов выглядит следующим образом:
Model Summary (Сводная таблица по модели)
| Model (Модель) | R | R Square (R-квадрат) | Adjusted R Square (Скорректир. R-квадрат) | Std. Error of the Estimate (Стандартная ошибка оценки) |
| 1 | ,861 а | ,741 | ,740 | 25,26 |
а. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константы), холестерин, исходная величина)
| Model (Модель) | Sum of Squares (Сумма Квадратов) | df | Mean Square (Среднее значение квадрата) | F | Sig. (Значимость) | |
| 1 | Regression (Регрессия) | 314337,948 | 1 | 314337,9 | 492,722 | ,000 a |
| Residual (Остатки) | 109729,408 | 172 | 637,962 | |||
| Total (Сумма) | 424067,356 | 173 |
a. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константа), холестерин, исходная величина).
b. Dependent Variable: Cholesterin, nach 1 Monat (Зависимая переменная холестерин через 1 месяц)
Coefficients (Коэффициенты) а
| Model (Модель) | Unstandardized Coefficients (Не стандартизированные коэффициенты) | Standardized Coefficients (Стандартизированные коэффициенты) | t | Sig. (Значимость) | |
| B | Std: Error (Станд. ошибка) | ß (Beta) | |||
| 1 | (Constant) (Константа) | 34,546 | 9,416 | 3,669 | ,000 |
| Cholesterin, Ausgangswert | ,863 | ,039 | ,861 | 22,197 | ,000 |
a. Dependent Variable (Зависимая переменная)
Рассмотрим сначала нижнюю часть результатов расчётов. Здесь выводятся коэффициент регрессии b и смещение по оси ординат а под именем «константа». То есть, уравнение регрессии выглядит следующим образом:
chol1 = 0,863 • chol0 + 34,546
Если значение исходного показателя холестерина составляет, к примеру, 280, то через один месяц можно ожидать показатель равный 276.
Частные рассчитанных коэффициентов и их стандартная ошибка дают контрольную величину Т; соответственный уровень значимости относится к существованию ненулевых коэффициентов регрессии. Значение коэффициента ß будет рассмотрено при изучении многомерного анализа.
Средняя часть расчётов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию, которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется «коэфициентом детерминации». В таблице результатов это частное выводится под именем «R-квадрат». В нашем примере мера определённости равна:
314337,948 / 424067,356 = 0,741
Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными. Мера определённости всегда лежит в диапазоне от 0 до 1. Существование ненулевых коэффициентов регрессии проверяется посредством вычисления контрольной величины F, к которой относится соответствующий уровень значимости.
В простом линейном регрессионном анализе квадратный корень из коэфициента детерминации, обозначаемый «R», равен корреляционному коэффициенту Пирсона. При множественном анализе эта величина менее наглядна, нежели сам коэфициент детерминации. Величина «Cмещенный R-квадрат» всегда меньше, чем несмещенный. При наличии большого количества независимых переменных, мера определённости корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать, глядя на соответствующую диаграмму рассеяния. Кроме того, в пользу гипотезы о линейной связи говорит также высокий уровень дисперсии, описываемой уравнением регрессии.
И, наконец, стандартизированные прогнозируемые значения и стандартизированные остатки можно предоставить в виде графика. Вы получите этот график, если через кнопку Plots. (Графики) зайдёте в соответствующее диалоговое окно и зададите в нём параметры *ZRESID и *ZPRED в качестве переменных, отображаемых по осям у и х соответственно. В случае линейной регрессии остатки распределяются случайно по обе стороны от горизонтальной нулевой линии.
Сохранение новых переменных
Многочисленные вспомогательные значения, рассчитываемые в ходе построения уравнения регрессии, можно сохранить как переменные и использовать в дальнейших расчётах.
Для этого в диалоговом окне Linear Regression (Линейная регрессия) щёлкните на кнопке Save (Сохранить). Откроется диалоговое окно Linear Regression: Save (Линейная регрессия: Сохранение) как изображено на рисунке 16.3.
Рис. 16.3: Диалоговое окно Линейная регрессия: Сохранение
Интересными здесь представляются опции Standardized (Стандартизированные значения) и Unstandardized (Нестандартизированные значения), которые находятся под рубрикой Predicted values (Прогнозируемые величины опции). При выборе опции Не стандартизированные значения будут рассчитывается значения у, которое соответствуют уравнению регрессии. При выборе опции Стандартизированные значения прогнозируемая величина нормализуется. SPSS автоматически присваивает новое имя каждой новообразованной переменной, независимо от того, рассчитываете ли Вы прогнозируемые значения, расстояния, прогнозируемые интервалы, остатки или какие-либо другие важные статистические характеристики. Нестандартизированным значениям SPSS присваивает имена pre_1 (predicted value), pre_2 и т.д., а стандартизированным zpr_l.
Щёлкните в диалоговом окне Linear Regression: Save (Линейная регрессия: Сохранение) в поле Predicted values (Прогнозируемые значения) на опции Unstandardized (Нестандартизированные значения).
Подтвердите нажатием Continue (Далее) и в заключение ОК.
В редакторе данных будет образована новая переменная под именем рrе_1 и добавлена в конец списка переменных в файле. Для объяснения значений, находящихся в переменной рrе_1, возьмём случай 5. Для случая 5 переменная рrе_1 содержит нестандартизированное прогнозируемое значение 263,11289. Это прогнозируемое значение слегка отличается в сторону увеличения от реального показателя содержания холестерина, взятого через один месяц (chol1) и равного 260. Нестандартизированное прогнозируемое значение для переменной chol1, так же как и другие значения переменной рге_1, было вычислено исходя из соответствующего уравнения регрессии.
Если мы в уравнение регрессии:
chol1 = 0,863 • chol0 + 34,546
подставим исходное значение для chol0 (265), то получим: chol1 = 0,863 • 265 + 34,546 = 263,241
Небольшое отклонение от значения, хранящегося в переменной рге_1 объясняется тем, что SPSS использует в расчётах более точные значения, чем те, которые выводятся в окне просмотра результатов.
Добавьте для этого в конец файла hyper.sav, ещё два случая, используя фиктивные значения для переменной chol0. Пусть к примеру, это будут значения 282 и 314.
Мы исходим из того, что нам не известны значения показателя холестерина через месяц после начала лечения, и мы хотим спрогнозировать значение переменной chol1.
Оставьте предыдущие установки без изменений и проведите новый расчёт уравнения регрессии.
В конце списка переменных добавится переменная рге_2. Для нового добавленного случая (№175) для переменной chol1 будет предсказано значение 277,77567, а для случая №176 — значение 305,37620.
Построение регрессионной прямой
Чтобы на диаграмме рассеяния изобразить регрессионную прямую, поступите следующим образом:
Выберите в меню следующие опции Graphs . (Графики) / Scatter plots. / Диаграммы рассеяния. Откроется диалоговое окно Scatter plots. (Диаграмма рассеяния) — (рис. 16.4).
Рис. 16.4: Диалоговое окно Scatter plots. (Диаграмма рассеяния)
В диалоговом окне Scatter plots. (Диаграмма рассеяния) оставьте предварительную установку Simple (Простая) и щёлкните на кнопке Define (Определить). Откроется диалоговое окно Simple Scatter plot (Простая диаграмма рассеяния) (рис. 16.5).
Рис. 16.5: Диалоговое окно Simple Scatterplot (Простая диаграмма рассеяния).
Перенесите переменную chol1 в поле оси Y, а переменную chol0 в поле оси X.
Подтвердите щелчком на ОК. В окне просмотра результатов появится диаграмма рассеяния (рис. 16.6).
Рис. 16.6: Диаграмма рассеяния в окне просмотра
Щёлкните дважды на этом графике, чтобы перенести его в редактор диаграмм.
Выберите в редакторе диаграмм меню Chart. (Диаграмма) / Options. (Опции). Откроется диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния) (рис. 16.7).
Рис. 16.7: Диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния)
В рубрике Fit Line (Приближенная кривая) поставьте флажок напротив опции Total (Целиком для всего файла данных) и щёлкните на кнопке Fit Options (Опции для приближения). Откроется диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния: приближенная кривая) (см. рис. 16.8).
Рис. 16.8: Диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния:
Подтвердите предварительную установку Linear Regression (Линейная регрессия) щелчком Continue (Далее) и затем на ОК.
Закройте редактор диаграмм и щёлкните один раз где-нибудь вне графика. Теперь в диаграмме рассеяния отображается регрессионная прямая (рис. 16.9).
Рис. 16.9: Диаграмма рассеяния с регрессионной прямой
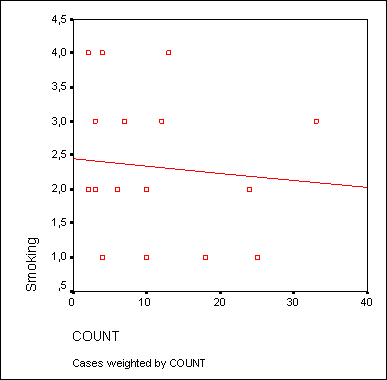
Для диаграмм рассеяния часто оказывается необходимой дополнительная корректировка осей. Продемонстрируем такую коррекцию при помощи одного примера. В файле raucher.sav находятся десять фиктивных наборов данных. Переменная konsum указывает на количество сигарет, которые выкуривает один человек в день, а переменная puls на количество времени, необходимое каждому испытуемому для восстановления пульса до нормальной частоты после двадцати приседаний. Как было показано ранее, постройте диаграмму рассеяния с внедрённой регрессионной прямой.
В диалоговом окне Simple Scatterplot (Простая диаграмма рассеяния) перенесите переменную puls в поле оси Y, а переменную konsum — в поле оси X. После соответствующей обработки данных в окне просмотра появится диаграмма рассеяния, изображённая на рисунке 16.10.
Рис. 16.10: Диаграмма рассеяния с регрессионной прямой до коррекции осей
Так как никто не выкуривает минус 10 сигарет в день, точка начала отсчёта оси X является не совсем корректной. Поэтому эту ось необходимо откорректировать.
Дважды щёлкните на графике и в меню редактора диаграмм вберите опции Chart. (Диаграмма) / Axis. (Оси). Откроется диалоговое окно Axis Selection (Выбор оси) (рис. 16.11).
Рис. 16.11: Диалоговое окно Axis Selection (Выбор оси)
Подтвердите предварительный выбор оси X нажатием кнопки ОК. Откроется диалоговое окно X-Scale Axis (Ось X) (рис. 16.12).
Рис. 16.12: Диалоговое окно X-Scale Axis (Ось X)
В редактируемом поле Displayed (Отображаемый) в рубрике Range (Диапазон) измените минимальное значение на 0.
Подтвердите нажатием на ОК.
Выберите вновь в меню редактора диаграмм опции Chart. (Диаграмма* Axis. (Оси)
Активируйте в диалоговом окне Axis Selection (Выбор оси) опцию Y Scale (Ось Y). Откроется диалоговое окно Y-Scale Axis (Ось Y).
И здесь в рубрике Range (Диапазон) в редактируемом поле Displayed (Отображаемый) измените минимальное значение на «0».
Подтвердите нажатием на ОК.
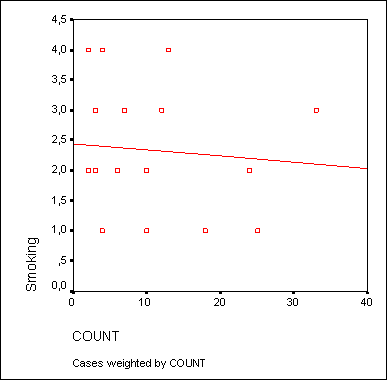
В окне просмотра Вы увидите откорректированную диаграмму рассеяния (см. рис. 16.13).
Рис. 16.13: Диаграмма рассеяния с регрессионной прямой после корректировки осей
На откорректированной диаграмме рассеяния теперь стало проще распознать начальную точку на оси Y, которая образуется при пересечении с регрессионной прямой. Значение этой точки примерно равно 2,9. Сравним это значение с уравнением регрессии для переменных puls (зависимая переменная) и konsum (независимая переменная). В результате расчёта уравнения регрессии в окне отображения результатов появятся следующие значения:
Coefficients (Коэффициенты) а
| Model (Модель) | Unstandardized Coefficients (Не стандартизированные коэффициенты) | Standardized Coefficients (Стандартизированные коэффициенты) | t | Sig. (Значимость) | |
| B | Std: Error (Станд. ошибка) | ß (Beta) | |||
| 1 | (Constant) (Константа) | 2,871 | ,639 | 4,492 | ,002 |
| tgl. Zigarettenkonsum | ,145 | ,038 | ,804 | 3,829 | ,005 |
a. Dependent Variable: Pulsfrequenz unter 80 (Зависимая переменная: частота пульса ниже 80)
Что дает следующее уравнение регрессии:
puls = 0,145 • konsum + 2,871
Константа в вышеприведенном уравнении регрессии (2,871) соответствует точке на оси Y, которая образуется в точке пересечения с регрессионной прямой.
Видео:Тема по SPSS: множественная линейная регрессия - одновременное включение всех переменных в модель.Скачать

Множественная линейная регрессия в SPSS
Множественная линейная регрессия (multiple linear regression) – подход к моделированию связи между одной зависимой переменной и несколькими независимыми.
Случай, когда линейная регрессия имеет только одну зависимую переменную и одну независимую, называется простой линейной регрессией (simple linear regression) или парной линейной регрессией (bivariate regression).
Начнём рассмотрение с простого варианта. Парная линейная регрессия, содержащая только одну зависимую переменную и одну независимую, имеет уравнение вида:






Графически указанные величины будут представлены следующим образом. Предсказанные значения зависимой переменной – это те точки, через которые пройдёт линия регрессии. Интерсепт показывает, чему будет равно y при x = 0. Угловой коэффициент показывает, насколько прирастёт y, если x изменится на 1 единицу. Наконец, случайные ошибки модели, возникающие вследствие влияния неучтённых моделью факторов, увидеть нельзя. Но мы можем увидеть наблюдаемую ошибку, которая называется остатками модели (residuals) – это разность между тем, где находятся наблюдения, и тем, где проходит линия регрессии.
Вычисление величин, отличных от наблюдаемых, производится методом наименьших квадратов (least-squares method). Этот метод позволяет построить зависимость величин таким образом, чтобы линия проходила наиболее близко ко всем наблюдаемым случаям. К тому же метод наименьших квадратов гарантирует, что существует только один-единственный способ, как именно можно провести эту линию при заданных условиях.
Рассмотрим на графике рассеяния указанные в уравнении величины:
В формулу интерсепта входит коэффициент корреляции r-Пирсона, что приводит к прямому соответствию между знаком коэффициента корреляции и направлением линии относительно диагоналей графика рассеяния. При положительной корреляции линия регрессии будет проходить так, как указано на рисунке; в случае отрицательной корреляции интерсепт также будет отрицательным, а линия регрессии пойдёт по другой диагонали графика. В случае приближения корреляции к нулю, линия регрессии будет более-менее параллельна оси X.
Простая линейная регрессия, отражённая на рисунке, представляет собой попытку найти зависимость, связывающую X и Y. К искомой зависимости предъявляется ряд требований, среди которых самыми важными на первоначальном этапе понимания являются два: 1) зависимость должна иметь вид линии, что мы можем видеть как графически, так и в самом уравнении; 2) результат нашего моделирования необходимо проверить, ведь построенная линия сама по себе не означает, что зависимость есть. Отличие успешной модели от неуспешной состоит не в том, что у неуспешной модели нет линии. Отличие состоит в том, что линия неуспешной модели параллельна оси Х или, если говорить более точными формулировками, угловой коэффициент такой линии не отличается от ноля. Поэтому при расчёте в SPSS мы должны понять, какими способами оценивается успешность построения модели. В общем смысле для оценки успешности построения модели нам необходимо, чтобы наблюдаемые значения оказались как можно ближе к линии регрессии (лучше, чтобы они находились на ней). Не стоит путать это высказывание со способом построения линии – методом наименьших квадратов. Ведь если зависимости нет, линия наименьших квадратов, хотя и пройдёт ближе всего к точкам, будет фактически очень далеко от каждой из них. К тому же для оценки успешности построения модели нам важно, чтобы угол линии был достаточно большой, ведь в обратном случае изменение X не приводит к изменению Y.
При увеличении количества независимых переменных простая линейная регрессия становится множественной. Уравнение сохраняет общую логику, хотя и приобретает расширенный вид:
В этом уравнении мы также встречаем интерсепт и угловой коэффициент, а отличие состоит лишь в том, что происходит введение нескольких независимых переменных, каждая из которых имеет свой угловой коэффициент. К сожалению, на двухмерном графике нельзя увидеть трёхмерную картину линейной регрессии, а при добавлении факторов наше физическое пространство и мироощущение вовсе оказываются неподготовленными к графическому восприятию обсуждаемого вопроса. Однако это никак не мешает вычислять требуемые величины аналитически.
Перед тем, как начать конкретный расчёт множественной линейной регрессии в SPSS, стоит сделать ещё одно общее замечание. В модели присутствует сразу несколько независимых переменных, но исследователь не может быть уверен, что каждая из них действительно должна быть включена в модель. С одной стороны, расчёт позволит ответить на этот вопрос. С другой, из-за того, как именно происходит вычисление, неправильно введённая в модель переменная может кардинальным образом повлиять на вывод относительно всех переменных. Поэтому были разработаны различные способы включения переменных в модель:
- Enter – это одновременное введение всех переменных в модель.
- Forward (переадресовать/вперёд) – это способ, при котором рассуждение начинается с отсутствия независимых переменных в модели. Из имеющегося пула «кандидатов» выбирается только тот, который наилучшим образом соответствует предъявленному требованию наибольшей корреляции с зависимой переменной (определяемой наименьшим значением уровня значимости t-критерия в пределах до 0,05). Если такой «кандидат» обнаруживается, он включается в модель. Затем из оставшегося пула выбирается следующий «кандидат», который имеет наибольшую корреляцию с зависимой переменной (наименьшее значение уровня значимости t-критерия до 0,05).
- Backward (назад) – это способ, противоположный по своей логике способу Forward. Рассуждение начинается с присутствия всех независимых переменных в модели. Затем выбирается тот «кандидат», который имеет наименьшую корреляцию с зависимой переменной (наибольшее значение уровня значимости t-критерия, начиная с 0,10). После исключения этого «кандидата» происходит новая оценка модели, приводящая к исключению следующего «кандидата» с наименьшей корреляцией.
- Stepwise (пошагово) – это сочетание методов forward и backward. Начинается рассуждение с отсутствия независимых переменных в модели. Из пула «кандидатов» выбирается тот, который имеет наибольшую корреляцию. Затем добавляется следующий, имеющий наибольшую корреляцию. Но на этом этапе идёт переоценка модели и, если введение нового «кандидата» привело к изменению показателей, происходит исключение какой-либо из ранее введённых переменных при достижении критериев исключения. Далее продолжается поиск подходящих «кандидатов» из пула. Т.е. это отбор переменных с учётом как критерия включения, так и критерия исключения.
- Remove (удалить) – применяется в иерархической линейной регрессии (hierarchical linear regression), поскольку удаляет все переменные из блока.
К сожалению, однозначного ответа на вопрос, какой из указанных методов лучше, нет. На мой взгляд, имеет смысл начинать с одновременного включения всех переменных в модель (enter), чтобы оценить общую картину. А итоговый расчёт можно проводить каким-либо из методов 2, 3, 4. Основной интерес при сравнении указанных методов будет представлять наличие или отсутствие различия в выводах. Если применение различных методов приводит к различным выводам, необходимо более пристальное внимание к тем переменным, которые начинают появляться и пропадать в разных моделях. Это связано с критериями включения и исключения, отличающимися от метода к методу. Исследователю стоит самостоятельно принять решение, какую модель выбрать. Но, с моей точки зрения, имеет смысл исключить из модели все переменные, которые попадают в промежуток между уровнями значимости от 0,05 до 0,10.
Исходные данные для расчёта множественной регрессии в SPSS, а также гипотезы и базовые предположения представлены в документе: исходные данные — множественная линейная регрессия
На видео 1 представлен расчёт множественной линейной регрессии в SPSS методом одновременного включения всех переменных в модель:
На видео 2 представлен расчёт множественной линейной регрессии различными методами включения переменных в модель:
На видео 3 рассмотрена проверка базовых предположений множественной линейной регрессии:
На видео 4 представлена проверка многомерной нормальности в SPSS:
Синтаксисы , полезные при расчёте множественной линейной регрессии:
проверка многомерной нормальности: макрос и синтаксис многомерной нормальности, а также пояснение, как запустить эту проверку.
📺 Видео
Множественная линейная регрессия в SPSSСкачать

Простая линейная регрессия 1Скачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Тема по SPSS: способы включения переменных в модель множественной линейной регрессии.Скачать

Linear Regression 1 / Линейная регрессия 1Скачать

Множественная регрессия в программе SPSS (Multiple regression)Скачать

Лекция 2.1: Линейная регрессия.Скачать

Линейная регрессияСкачать

нелинейная регрессияСкачать

Тема по SPSS: проверка базовых предположений множественной линейной регрессии.Скачать

Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Линейная регрессияСкачать

Множественный регрессионный анализ в SPSS,Statistica. multiple regression in spss and StatisticaСкачать

Множественная регрессияСкачать

Линейная регрессия НачалоСкачать

Что такое линейная регрессия? Душкин объяснитСкачать

Linear Regression 2 / Линейная регрессия 2Скачать

Лекция 8. Линейная регрессияСкачать