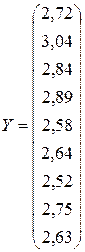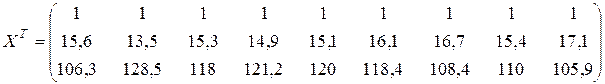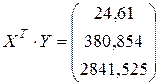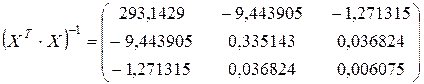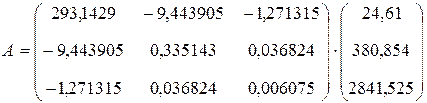Уравнение линейной регрессии в матричной форме

Дата публикации 2018-03-05

Линейная регрессия — это метод моделирования отношений между одной или несколькими независимыми переменными и зависимой переменной.

Это основной продукт статистики, который часто считается хорошим начальным методом машинного обучения. Это также метод, который может быть переформулирован с использованием матричной записи и решен с использованием матричных операций.

В этом уроке вы узнаете матричную формулировку линейной регрессии и способы ее решения с использованием методов прямой и матричной факторизации.

После завершения этого урока вы узнаете:

• Линейная регрессия и переформулировка матрицы с помощью нормальных уравнений.
• Как решить линейную регрессию с использованием декомпозиции матрицы QR.
• Как решить линейную регрессию, используя SVD и псевдообратную.

Обзор учебника

Этот урок разделен на 6 частей; они есть:

1. Линейная регрессия
2. Матричная формулировка линейной регрессии
3. Набор данных линейной регрессии
4. Решить напрямую
5. Решить с помощью QR-разложения
6. Решить через разложение по сингулярному значению

Линейная регрессия

Линейная регрессия — это метод моделирования отношений между двумя скалярными значениями: входной переменной x и выходной переменной y.

Модель предполагает, что y является линейной функцией или взвешенной суммой входной переменной.

Или указано с коэффициентами.

Модель также можно использовать для моделирования выходной переменной с учетом нескольких входных переменных, называемых многомерной линейной регрессией (ниже для удобства чтения были добавлены скобки).

Цель создания модели линейной регрессии состоит в том, чтобы найти значения для значений коэффициента (b), которые минимизируют ошибку в прогнозировании выходной переменной y.

Матричная формулировка линейной регрессии

Линейная регрессия может быть задана с использованием матричной записи; например:

Или без точечной записи.

Где X — входные данные, а каждый столбец — объект данных, b — вектор коэффициентов, а y — вектор выходных переменных для каждой строки в X.

Переформулированная задача превращается в систему линейных уравнений, в которой значения вектора b неизвестны. Система такого типа упоминается как переопределенная, потому что существует больше уравнений, чем неизвестных, то есть каждый коэффициент используется в каждой строке данных.

Это сложная проблема для решения аналитически, потому что есть несколько противоречивых решений, например, несколько возможных значений для коэффициентов. Кроме того, все решения будут иметь некоторую ошибку, потому что нет линии, которая будет проходить почти через все точки, поэтому подход к решению уравнений должен быть в состоянии справиться с этим.

Как правило, это достигается путем нахождения решения, в котором значения b в модели минимизируют квадратичную ошибку. Это называется линейным методом наименьших квадратов.

Эта формулировка имеет уникальное решение, если входные столбцы независимы (например, некоррелированы).

Мы не всегда можем получить ошибку e = b — Ax до нуля. Когда e равно нулю, x является точным решением Ax = b. Когда длина е настолько мала, насколько это возможно, это решение наименьших квадратов.

В матричной записи эта проблема формулируется с использованием так называемого нормального уравнения:

Это может быть переупорядочено, чтобы указать решение для b как:

Это может быть решено напрямую, хотя наличие обратной матрицы может быть численно сложным или нестабильным.

Набор данных линейной регрессии

Чтобы изучить матричную формулировку линейной регрессии, давайте сначала определим набор данных как контекст.

Мы будем использовать простой 2D-набор данных, в котором данные легко визуализировать в виде точечной диаграммы, а модели легко представить в виде линии, которая пытается соответствовать точкам данных.

Приведенный ниже пример определяет матричный набор данных 5 × 2, разбивает его на компоненты X и y и строит набор данных как график рассеяния.

При запуске примера сначала печатается определенный набор данных.

Затем создается точечная диаграмма набора данных, показывающая, что прямая линия не может точно соответствовать этим данным.

Решить напрямую

Первый подход — попытаться решить проблему регрессии напрямую.

То есть, учитывая X, каков набор коэффициентов b, который при умножении на X даст y. Как мы видели в предыдущем разделе, нормальные уравнения определяют, как вычислять b напрямую.

Это можно вычислить непосредственно в NumPy, используя функцию inv () для вычисления обратной матрицы.

После того как коэффициенты рассчитаны, мы можем использовать их для прогнозирования результатов с учетом X.

Объединяя это с набором данных, определенным в предыдущем разделе, полный пример приведен ниже.

При выполнении примера выполняется вычисление и выводится вектор коэффициента b.

Затем создается точечная диаграмма набора данных с линейным графиком для модели, показывающим разумное соответствие данным

Проблема с этим подходом — обратная матрица, которая является вычислительно дорогой и численно нестабильной. Альтернативный подход заключается в использовании матричной декомпозиции, чтобы избежать этой операции. Мы рассмотрим два примера в следующих разделах.

Решить с помощью QR-разложения

QR-разложение — это подход к разбивке матрицы на составляющие ее элементы.

Где A — матрица, которую мы хотим разложить, Q — матрица с размером m x m, а R — верхняя треугольная матрица с размером m x n.

QR-разложение является популярным подходом для решения линейного уравнения наименьших квадратов.

Переходя ко всему выводу, коэффициенты могут быть найдены с использованием элементов Q и R следующим образом:

Подход все еще включает матричную инверсию, но в этом случае только на более простой R-матрице.

QR-разложение можно найти с помощью функции qr () в NumPy. Расчет коэффициентов в NumPy выглядит следующим образом:

Связав это с набором данных, полный пример приведен ниже.

Выполнение примера сначала печатает решение коэффициента и наносит на график данные с моделью.

Подход QR-разложения более эффективен в вычислительном отношении и более численно стабилен, чем прямой расчет нормального уравнения, но не работает для всех матриц данных.

Решить через разложение по сингулярному значению

Разложение по сингулярному значению, или сокращенно SVD, — это метод матричной декомпозиции, такой как QR-декомпозиция.

Где A — вещественная матрица nxm, которую мы хотим разложить, U — матрица amxm, Sigma (часто представляемая заглавной греческой буквой Sigma) — диагональная матрица mxn, а V ^ * — сопряженная транспонирование матрицы nxn, где * — верхний индекс.

В отличие от разложения QR, все матрицы имеют разложение SVD. В качестве основы для решения системы линейных уравнений для линейной регрессии SVD является более устойчивым и предпочтительным подходом.

После разложения коэффициенты могут быть найдены путем вычисления псевдообращения входной матрицы X и умножения ее на выходной вектор y.

Где псевдообратный рассчитывается следующим образом:

Где X ^ + — псевдообратная X, а + — верхний индекс, D ^ + — псевдообратная диагональная матрица Sigma, а V ^ T — транспонирование V ^ *.

Инверсия матриц не определена для матриц, которые не являются квадратными. […] Когда A имеет больше столбцов, чем строк, то решение линейного уравнения с использованием псевдообратного представления дает одно из многих возможных решений.

Мы можем получить U и V из операции SVD. D ^ + можно рассчитать, создав диагональную матрицу из Sigma и вычислив обратную величину каждого ненулевого элемента в Sigma.

Мы можем вычислить SVD, затем псевдообратную вручную. Вместо этого NumPy предоставляет функцию pinv (), которую мы можем использовать напрямую.

Полный пример приведен ниже.

При выполнении примера печатается коэффициент и данные отображаются красной линией, показывающей прогнозы из модели.

Фактически, NumPy предоставляет функцию для замены этих двух шагов в функции lstsq (), которую вы можете использовать напрямую.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Реализация линейной регрессии с использованием встроенной функции lstsq () NumPy
• Проверьте каждую линейную регрессию на своем собственном маленьком вымышленном наборе данных.
• Загрузите набор табличных данных и протестируйте каждый метод линейной регрессии и сравните результаты.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

• Раздел 7.7. Наименьшие квадраты приближенных решений.Руководство по линейной алгебре, 2017
• Раздел 4.3 Аппроксимации наименьших квадратов,Введение в линейную алгебру, Пятое издание, 2016.
• Лекция 11, Проблемы наименьших квадратов,Численная линейная алгебра, 1997.
• Глава 5, Ортогонализация и наименьшие квадраты,Матричные вычисления2012.
• Глава 12, Сингулярное значение и разложение Джордана,Линейная алгебра и матричный анализ для статистики2014
• Раздел 2.9. Псевдообращение Мура-Пенроуза.Глубокое обучение, 2016
• Раздел 15.4 Генеральные линейные наименьшие квадраты,Численные рецепты: искусство научных вычисленийТретье издание, 2007.

статьи

Учебники

Резюме

В этом руководстве вы обнаружили матричную формулировку линейной регрессии и способы ее решения с использованием методов прямой и матричной факторизации.

В частности, вы узнали:

• Линейная регрессия и переформулировка матрицы с помощью нормальных уравнений.
• Как решить линейную регрессию с использованием декомпозиции матрицы QR.
• Как решить линейную регрессию, используя SVD и псевдообратную.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Уравнение множественной регрессии

Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:

• уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
• множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;

Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Отбор факторов обычно осуществляется в два этапа:

1. теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
2. количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.

Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X

1	5	14.5
1	12	18
1	6	12
1	7	13
1	8	14

Матрица Y

9

13

16

14

21

Транспонируем матрицу X, получаем X T :

1	1	1	1	1
5	12	6	7	8
14.5	18	12	13	14

Умножаем матрицы, X T X =

5 38 71,5 38 318 563,5 71,5 563,5 1043,25

В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X

Умножаем матрицы, X T Y =

73 563 1032,5

Находим обратную матрицу (X T X) -1

13.99	0.64	-1.3
0.64	0.1	-0.0988
-1.3	-0.0988	0.14

Вектор оценок коэффициентов регрессии равен

(X T X) -1 X T Y = y(x) =

13,99 0,64 -1,3 0,64 0,1 -0,0988 -1,3 -0,0988 0,14

*

73 563 1032,5

=

34,66 1,97 -2,45

Получили оценку уравнения регрессии: Y = 34.66 + 1.97X₁-2.45X₂
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 _e/∑(y_i — y_ср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X₁ (%), а также по уровню инфляции X₂ (%).

Год	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X1	3,5	2,8	6,3	4,5	3,1	1,5	7,6	6,7	4,2	2,7	4,5	3,5	5,0	2,3	2,8
X2	4,5	3,0	3,1	3,8	3,8	1,1	2,3	3,6	7,5	8,0	3,9	4,7	6,1	6,9	3,5
Y	9,0	6,0	8,9	9,0	7,1	3,2	6,5	9,1	14,6	11,9	9,2	8,8	12,0	12,5	5,7

Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X₁ + 1.4798X₂
Скачать.

Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).

Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.

ВВП	16331,97	16763,35	17492,22	18473,83	19187,64	20066,25	21281,78	22326,86	23125,90
Потребление в текущих ценах	771,92	814,28	735,60	788,54	853,62	900,39	999,55	1076,37	1117,51
Инвестиции в текущих ценах	176,64	173,15	151,96	171,62	192,26	198,71	227,17	259,07	259,85

Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).

Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:

1. Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
2. Рассчитать частные коэффициенты эластичности. Сделать вывод.
3. Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
5. Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.

Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

Матрица Y

7
7
7
7
7
7
8
8
8
10
9
11
9
11
12
12
12
12
14
14

Матрица X T

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

Умножаем матрицы, (X T X)

Умножаем матрицы, (X T Y)

Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1

Уравнение регрессии
Y = 1.8353 + 0.9459X ₁ + 0.0856X ₂
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s

0.62
0.28
0.38
0.01
0.11
-1
-0.57
0.29
-0.56
0.02
-0.31
1.23
-1.15
0.21
0.2
-0.07
-0.07
-0.53
0.34
0.57

se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

k(x) = 0.36

0,619 -0,0262 -0,0183 -0,0262 0,126 -0,0338 -0,0183 -0,0338 0,0102

=

0,222 -0,00939 -0,00654 -0,00939 0,0452 -0,0121 -0,00654 -0,0121 0,00366

Дисперсии параметров модели определяются соотношением S 2 _i = K_ii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)

Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции

Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл: T_табл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

Построение парной регрессионной модели

Рекомендации к решению контрольной работы.

Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.

Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x₁, дохода компании x₂ и объема инвестиций в расширение и модернизацию производства x₃. Исходные данные представлены выборкой объема n=50.

Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x₁, x₂, x₃ взятых по отдельности. Для каждой объясняющей переменной:

1. Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
2. Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации.
3. Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
4. Постройте на поле корреляции прямую линию выборочной регрессии по точкам .
5. Постройте диаграмму остатков.
6. Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение F_табл определите с помощью функции FРАСПОБР).
7. Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
8. Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
9. Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
10. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.

Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.

Матричный подход

Дата добавления: 2014-11-27 ; просмотров: 4058 ; Нарушение авторских прав

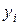
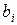
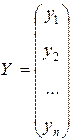
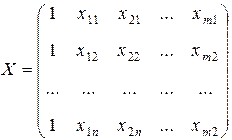
Построение модели линейной регрессии возможно проводить матричным методом. При этом результаты наблюдений , значения объясняющих переменных, параметры функции регрессии записываем в виде матриц:

, , .

При этом вводят переменные:

— вектор-столбец наблюдений над результативным показателем;

— матрица данных, причем первый столбец всегда состоит из единиц;

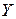
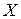
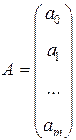
А — вектор-столбец коэффициентов регрессии.

Тогда уравнение регрессии в матричной форме имеет вид:

. (3.4.9)

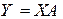
Используя МНК, получим в качестве решения системы нормальных уравнений вектор-столбец искомых параметров регрессии:

, (3.4.10)

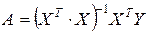
где 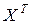— транспонированная матрица.

Таким образом, можем установить последовательность выполняемых действий:

· составить матрицу ;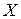

· выписать вектор ;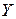

· получить транспонированную матрицу ;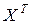

· найти произведение матриц ;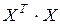

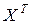
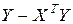
· найти произведение матрицы на вектор ;

· определить обратную матрицу ;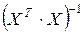

· составить произведение 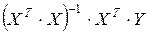, провести вычисления и определить вектор коэффициентов уравнения;

· записать моделирующее уравнение.

Переход к матричной форме позволяет, во-первых, представить алгоритм нахождения коэффициентов уравнения в более компактном конкретном виде, а во-вторых, использовать по этому алгоритму любой пакет программ, позволяющий проводить действия с матрицами.

Покажем на конкретном примере, как проводятся вычисления и находятся параметры линейного уравнения множественной регрессии.

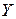
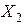
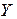Пример 3.9.Построить модель, которая характеризует зависимость между показателем , факторами и . Провести анализ взаимосвязи на основе полученной модели.

	2,72	3,04	2,84	2,89	2,58	2,64	2,52	2,75	2,63
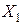	15,6	13,5	15,3	14,9	15,1	16,1	16,7	15,4	17,1
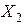	106,3	128,5	121,2	118,4	108,4	105,9

Решение.Оценим параметры модели по МНК. Выпишем основные матрицы, входящие в исследование:

,

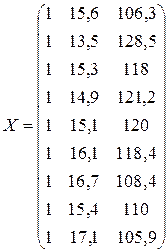
Замечание.

В матрице 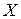всегда первый столбец состоит из единиц – это связано с присутствием в уравнении свободного члена .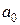

,

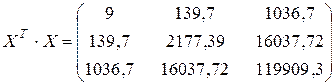
Найдем обратную матрицу:

Определим оценки параметров модели по формуле (3.4.11):

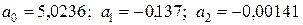
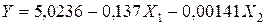
Таким образом, и искомая модель имеет вид:

.

Оценка коэффициентов уравнения

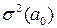
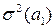
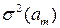
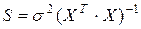
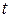
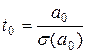
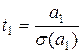
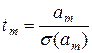
Оценку значимости коэффициентов уравнения также можно проводить на основе матричного подхода. Для этого вначале определяют дисперсии оценок параметров: , ,…, . Эти величины будут диагональными элементами матрицы: . После этого устанавливают -статистики по коэффициентам:

, ,…, ………………….(3.4.11)

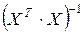
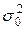
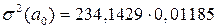
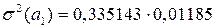
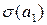
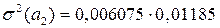
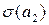
Для рассматриваемого примера 3.9 матрица известна. Если ее диагональные элементы умножить на = 0,011851, найденное по формуле (3.1.21) то получим такие результаты:

= 3,4739, = 1, 86385;

= 0,00397, = 0, 063021;

= 0,000072, = 0, 008485.

t – статистики Стьюдента, устанавливающие значимость коэффициентов регрессионного уравнения, определяются по формулам (3.4.11), и для рассматриваемого примера таковы:

;

;

.

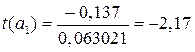
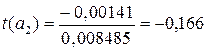
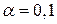
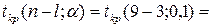
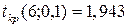
Зададим уровень значимости , тогда

.

Сравнивая значения t-статистик, можно сделать вывод, что коэффициент 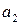является незначимыми.

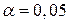
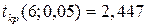
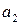
При уровне значимости имеем , поэтому коэффициенты и незначимы в построенном уравнении регресси.

3.4.3. Построение множественной регрессионной модели с использованием EXCEL

Уравнение линейной регрессии можно построить в пакете электронных таблиц Excel .

В состав пакета Excel входит набор способов анализа данных, который называется Пакетом анализа и предназначен для решения различных заданий. Для ознакомления с этим пакетом, следует в меню окна Excel выбрать опцию Сервис и в появившемся меню нужно выбрать опцию Анализ данных.В результате получим окно (рисунок 3.2).

Рисунок 3.2 – Окно Анализ данных

С помощью клавиш прокрутки можно выбрать любую из приведенных функций анализа.

Построение корреляционной матрицы

Пример 3.10. Построить корреляционную матрицу по следующим данным:

Y	X1	X2	X3
9,9	0,43	0,3	3,9
5,5	0,38	0,42	5,65
4,3	0,34	0,9	8,52
6,6	0,37	0,55	5,38
9,4	0,23	0,52	4,36
5,2	0,41	0,38	3,13
0,22	0,36	5,82

|	следующая лекция ==>
Построение множественной линейной регрессии	|	Решение.

Не нашли то, что искали? Google вам в помощь!

📹 Видео