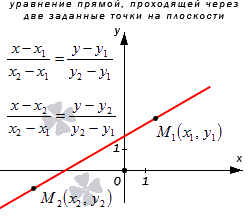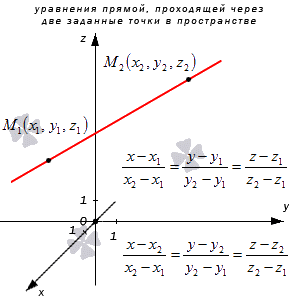Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
- Уравнение прямой, проходящей через две заданные точки на плоскости
- Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
- График линейной функции, его свойства и формулы
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Уравнение линейной функции проходящей через две точки
- 🌟 Видео
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .
Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .
Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .
Рассмотрим рисунок, приведенный ниже.
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .
Ответ: x + 5 6 = y — 2 3 — 5 6 .
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .
Приведем каноническое уравнение к искомому виду, тогда получим:
x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0
Ответ: x — 3 y + 2 = 0 .
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .
Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .
Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .
Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.
При подстановке получаем, что
— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3
Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .
Ответ: y = 2 3 x — 1 3 .
Видео:Видеоурок "Уравнение прямой, проходящей через две точки"Скачать
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .
Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .
По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:
x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5
Ответ: x — 2 — 1 = y + 3 0 = z — 5 .
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
График линейной функции, его свойства и формулы
О чем эта статья:
Видео:ЛИНЕЙНАЯ ФУНКЦИЯ | БАЗА | Как составить из 2 точек уравнение функции?Скачать
Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:Угловой коэффициент прямойСкачать
Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:Занятие 1. График линейной функции y=kx+bСкачать
Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:Как составить уравнение прямой, проходящей через две точки. Урок 3. Геометрия 8 класс.Скачать
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
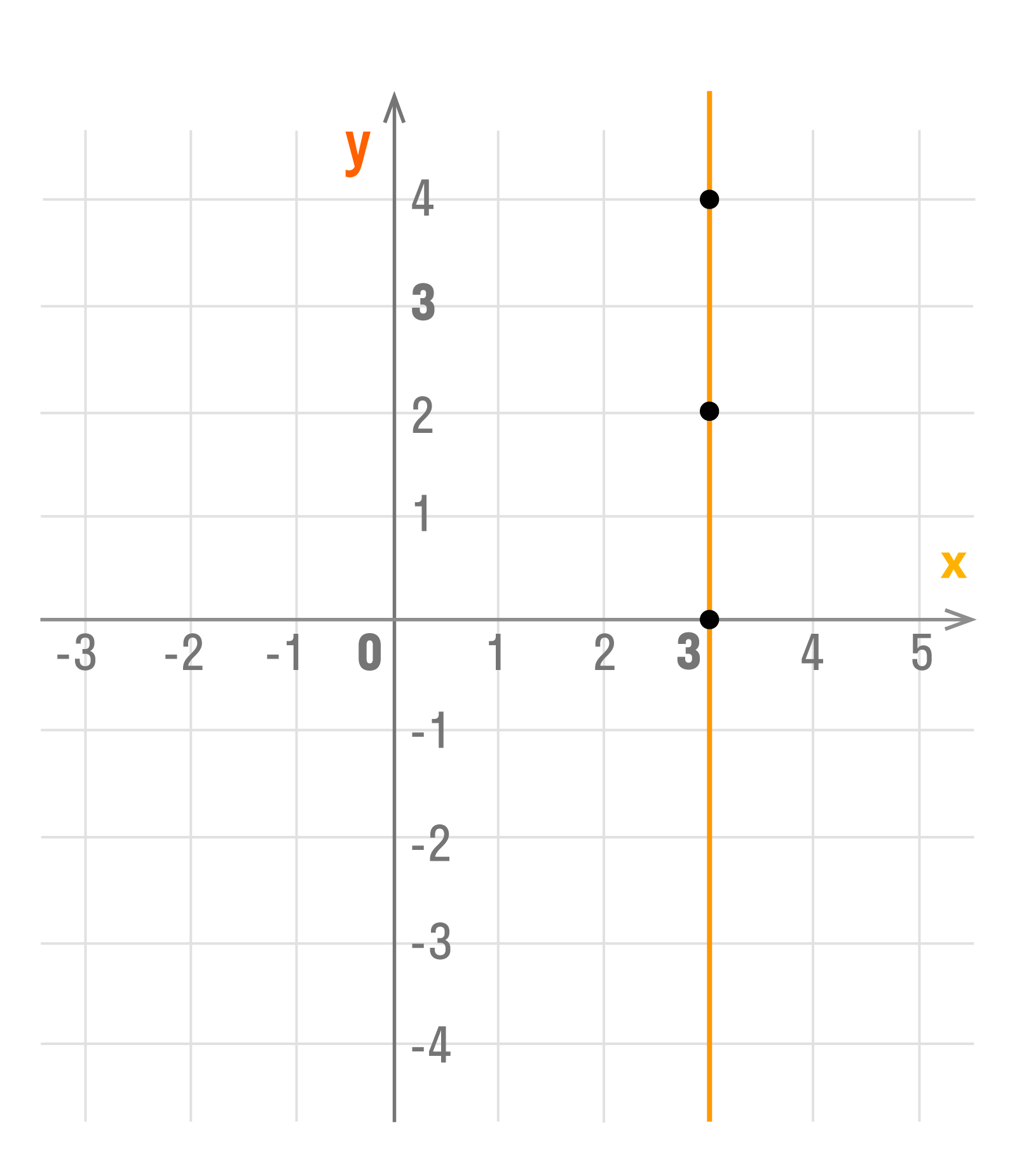
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:Уравнение прямой проходящей через две точки. Урок геометрии 9 класс.Скачать
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Видео:№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать
Уравнение линейной функции проходящей через две точки
Неверно введено число.
Точки должны быть разными.
Уравнение прямой по двум точкам
Введите координаты точек:
Количество знаков после разделителя дроби в числах:
Общее уравнение прямой:
Теория
Уравнение прямой, проходящей через две заданные точки (x1,y1) и (x2,y2), имеет вид:
или в общем виде
Т.е. получили общее уравнение прямой линии на плоскости в декартовых координатах:
🌟 Видео
Уравнение прямой, проходящей через две точки, и прямой, перпендикулярной заданной прямойСкачать
Уравнение прямой, проходящей через две заданные точкиСкачать
Составляем уравнение прямой по точкамСкачать
§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать
Уравнение прямой, проходящей через две точкиСкачать
Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать
Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать
Линейная функция и ее график. 7 класс.Скачать
Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать
