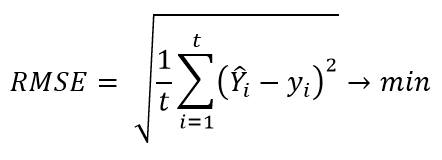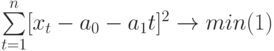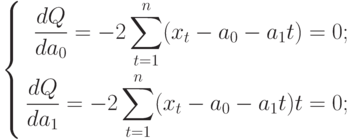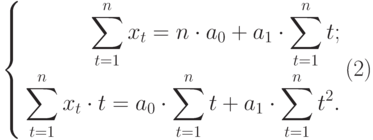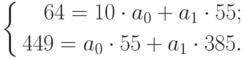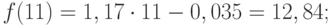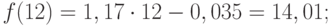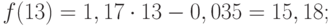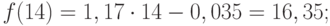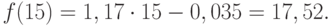- О линейном тренде
- Как мы можем скорректировать прогнозные значения тренда?
- Точных вам прогнозов!
- Присоединяйтесь к нам!
- Анализ временных рядов, тренд ряда динамики, точечная оценка прогноза
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- Анализ временных рядов
- Прогноз, характеристики и параметры прогнозирования
- Уравнение тренда временного ряда
- 📹 Видео
Пункт шестой — «Построение прогноза продаж: основные методы прогнозирования»
Наконец-то мы подобрались к самому основному шагу нашей карты данных — «Построение прогноза продаж». Здесь я вкратце расскажу, какие методы прогнозирования наиболее распространены и популярны и приведу формулы их использования. А в следующей части данной статьи, я расскажу об обработке получившегося прогноза: наложении сезонности, округлении, учете промо и так далее.
Напомню, что до этого мы проделали довольно большой путь: подготовили корректную историю продаж, очищенную от нестабильных показателей, рассчитали коэффициенты сезонности и промо-объемы будущих периодов и определились с элементами графического интерфейса (GUI) нашего будущего инструмента прогнозирования. А теперь, мы будем рассматривать методы прогнозирования и строить сам прогноз.
Классификация методов прогнозирования.
Методы прогнозирования делятся на две группы или класса: интуитивные (субъективные или качественные) и формализованные (объективные или количественные). Интуитивные методы прогнозирования — это такие методы, основой которых НЕ являются сухие расчеты, математика и статистика. Они, в первую очередь, основаны на оценках группы экспертов и предназначены для прогнозирования объемов новой позиции, у которой нет истории продаж. Либо для прогнозирования объемов позиции, история продаж которой настолько нестабильна, что невозможно подобрать под нее адекватную математическую модель. В пример можно привести такие методы, как «Метод Дельфи», «Мозговой штурм», «Опрос/анкетирование» и так далее, но в данной статье данные методы прогнозирования рассмотрены не будут.
Здесь будут рассмотрены следующие формализованные методы прогнозирования:
- Линейная регрессия
- Полиномиальный прогноз
- Экспоненциальное сглаживание
- Модель Хольта
- Модель Хольта-Винтерса
- Модель Тейла-Вейджа
Немного расскажу про каждый из них, а также затрону метод «прогнозирования по свойствам». А в конце статьи, помимо готового примера в Excel с формулами расчета, добавлю ссылки на некоторые источники информации о методах прогнозирования, может кому-то будет полезно.
Методы прогнозирования: метод линейной регрессии.
Построение прогноза с помощью метода линейной регрессии — один из наиболее простых, часто-встречающихся и распространенных (если рассматривать Excel) методов прогнозирования. Часто встречается он как раз из-за того, что в Excel его очень легко применить — достаточно воспользоваться функцией ЛИНЕЙН, ПРЕДСКАЗ или ТЕНДЕНЦИЯ, где исходными данными будут являться номера периодов и соответствующие им объемы продаж.
Для нахождения прогноза на период x, мы воспользуемся уравнением y=k*x+b, где k — угловой коэффициент, который находится с помощью метода наименьших квадратов (на основании предыдущих периодов x и соответствующих значений y), а b — это точка, в которой наш график пересекается с осью y. Данное уравнение описывает линию, которая называется линия тренда, которая показывает динамику продаж и прогнозы на последующие периоды.
На гистограмме ниже изображены столбцы с объемами продаж для соответствующего периода (номера недель по оси X), пунктирная линия, которая как раз является линией тренда и столбец c предсказанным значением (соответствует «продолжению» линии тренда):
Данный метод один из самых простейших, и чаще всего используется для прогнозирования более-менее стабильных и регулярных продаж, однако при максимально аккуратном «сглаживании» промо-объемов, он подойдет и для нестабильных рядов. Важно отметить, что если история продаж у нас не очень большая (менее 4-5 периодов), данный метод прогнозирования не рекомендуется к использованию.
Также важно, что если мы хотим добавить к прогнозному значению коэффициент сезонности, то для начала, перед расчетом прогнозного значения, историю продаж необходимо «выровнять», то есть очистить от сезонных колебаний. А уже потом считать прогноз и накладывать сезонность.
Хочу отметить, что в моем опыте работы данный метод прогнозирования в совокупности с корректным сглаживанием числового ряда, а также с корректными значениями планируемых промо-объемов, которые мне предоставлял отдел трейд-маркетинга, достигал достаточно высокой точности прогнозирования (выше 80%).
Методы прогнозирования: полиномиальный прогноз.
Построение прогноза с помощью полинома немного похоже на построение прогноза с помощью предыдущего метода. Здесь, для нахождения прогноза на последующие периоды вместо линейного уравнение, мы используем полином третьей степени вида y = a*x³+b*x²+c*x+d или полином второй степени вида y = a*x²+b*x+c, где коэффициенты a,b,c,d постоянны и находятся с помощью различных методов решения систем линейных уравнений, на основании предыдущих периодов x и соответствующим им объемов продаж y.
Если степень полинома будет выше третьей — линия, которой описывается наш числовой ряд будет максимально приближена к реальным значениям, но при этом будет не очень пригодна для построения прогноза (особенно, если строите прогноз сразу на несколько периодов). Как раз на примере ниже это очень заметно:
Полином пятой степени дает неудовлетворительные результаты в прогнозе.
Здесь используется полином пятой степени. Да, линия почти совпадает с фактическим значениям, но при этом даже невооруженным глазом видно, что прогноз на 31 и 32-ую неделю крайне неадекватный. Поэтому использовать полиномы выше третьей степени не рекомендуется.
Методы прогнозирования: модель на основе экспоненциального сглаживания.
Первоначально, модель экспоненциального сглаживания использовалась для сглаживания числового ряда. Однако, спустя какое-то время, данную модель немного видоизменили и приспособили для краткосрочного прогнозирования. Модель приемлема для нахождения прогноза только на 1 период вперед.
Для нахождения прогноза Y̅ на период t+1, используется следующая формула:
где yt — значение факта на период t, Y̅t — сглаженное значение на период t, а α — коэффициент или параметр сглаживания, который принимает значение 0 Методы прогнозирования: модель на основе экспоненциального сглаживания с учетом тренда (Метод Хольта).
Данная модель — усовершенствованная версия модели экспоненциального сглаживания с учетом тренда продаж.
Формула нахождения прогноза Y̅ на период t+d следующая:
где d — порядковый номер периода, на который мы делаем прогноз (то есть если числовой ряд состоит из 10 периодов, а прогноз мы делаем на 11, то d =1), а At и Bt — адаптивные переменные: A — экспоненциально-сглаженное фактическое значение , а B — значение тренда. Находятся данные переменные по следующим формулам:
И как в случае с обычным экспоненциальным сглаживанием, здесь тоже есть параметры, но их уже два: α1 и α2. И оба они принимают значения ∈(0,1). Подбирать эти параметры нужно так, чтобы прогнозы, построенные на уже имеющиеся периоды с фактическими значениями, с помощью полученной модели, давали наименьшую ошибку прогноза (во многих источниках рекомендуют использовать RMSE или MAPE). Напомню, для нахождения RMSE используется следующая формула:
Для нахождения A1 должно использоваться A0, но так как его не существует, мы, опять же, как и в случае с обычным экспоненциальным сглаживанием, вместо него используем фактическое значение y1, а вместо B1 используем 0.
Методы прогнозирования: модель на основе экспоненциального сглаживания с учетом тренда и мультипликативной сезонности (Метод Хольта-Винтерса).
Данная модель — тоже усовершенствованная версия модели экспоненциального сглаживания, только здесь помимо тренда, добавлена еще и мультипликативная сезонность. Подходит модель для работы с числовыми рядами, в которых присутствует ярко-выраженная сезонность или цикличность.
Формула расчета прогноза Y̅ на период t+d следующая:
где d — порядковый номер прогнозируемого периода (как и в предыдущем примере), L — это количество периодов в одном цикле (для месячного прогнозирования — 12, для квартального — 4, для ежедневного — 7). At и Bt — адаптивные переменные: A — экспоненциально-сглаженное фактическое значение, а B — значение тренда. А C с большим индексом «t+(d mod L) — L» — значение сезонности в процентах. Индекс переменной C может немного смутить, но на самом деле все проще, чем кажется: просто используем C из прошлого цикла соответствующего периода (для прогноза на март используем коэффициент сезонности марта прошлого цикла).
Сами переменные A,B и C рассчитываются по следующим формулам:
При использовании Метода Хольта-Винтерса рассчитывать коэффициенты сезонности перед построением не нужно, их расчет включен в формулу. Однако очищать числовой ряд от неадекватных значений все так же необходимо. Также, стоит отметить, что для корректной «работы» данной модели, история продаж должна содержать как минимум несколько циклов для корректного расчета сезонности (для месячного прогнозирования, необходима история продаж как минимум за 2-3 последних года).
Особенности расчета начальных переменных:
- Для A1 можно использовать y1
- Для B1 можно использовать 0
- В первом цикле при расчете A мы должны ссылаться на C прошлых циклов, но так как их нет, вместо C можно использовать 1 (то есть, пренебречь сезонностью)
- А для расчета сезонностей самого первого цикла(!) для каждого периода можно использовать формулу Ct=yt/At
Параметры α1,α2,α3 ∈(0,1), как и в предыдущей модели, подбираются путем минимизации ошибки прогноза (RMSE или MAPE).
Методы прогнозирования: модель на основе экспоненциального сглаживания с учетом тренда и аддитивной сезонности (Метод Тейла-Вейджа).
Данная модель также разработана на основе экспоненциального сглаживания, в которую добавлен тренд и сезонность, но теперь не мультипликативная, а аддитивная. Особенности здесь такие же, как и в методе Хольта-Винтерса. Основное отличие в том, что здесь сезонность является не коэффициентом, на который мы умножаем полученный прогноз, а целым числом, которое мы прибавляем или вычитаем из прогноза.
Формула расчета прогноза Y̅ на период t+d следующая:
где d — порядковый номер прогнозируемого периода (как и в предыдущем примере), L — это количество периодов в одном цикле (для месячного прогнозирования — 12, для квартального — 4, для ежедневного — 7). At и Bt — адаптивные переменные: A — сглаженное фактическое значение (с помощью экспоненты), а B — значение тренда. А C с большим индексом «t+(d mod L) — L» — значение сезонности в процентах.
Сами переменные A,B и C рассчитываются по следующим формулам:
Особенности расчета начальных переменных:
- Для A1 можно использовать y1
- Для B1 можно использовать 0
- В первом цикле при расчете A мы должны ссылаться на C прошлых циклов, но так как их нет, вместо C можно использовать 0 (то есть пренебречь сезонностью)
- А для расчета сезонностей самого первого цикла(!) для каждого периода можно использовать формулу Ct=yt-At
Параметры α1,α2,α3 ∈(0,1), как и в предыдущей модели, подбираются путем минимизации ошибки прогноза (RMSE или MAPE).
Методы прогнозирования: построение прогноза основанное на свойствах.
Данный способ довольно интересный, чаще всего используется для определения спроса какого-либо нового продукта. Его нельзя полноценно отнести к формализованному методу, но и интуитивным назвать его тоже нельзя.
Рассмотрим его суть на примере телевизора. Предположим, что этот телевизор — новинка на рынке и необходимо рассчитать его прогноз продаж. Для начала, мы рассматриваем свойства данного телевизора (его функции и характеристики), например такие:
- Диагональ экрана
- Фирма-изготовитель
- Разрешение экрана
- Наличие Smart-TV
- Возможность подключения USB
- Частота экрана
- Габариты
- Возможность крепления на стену
- Цвет
- Частота обновления экрана
- И так далее..
Далее, мы просматриваем статистику продаж других телевизоров и смотрим, как часто покупался какой-либо другой телевизор с тем или иным перечисленным свойством. И на основе всех этих данных, составляем некое уравнение, которое учтет частоту приобретения телевизора с каждым свойством по отдельности. И с помощью полученного уравнения рассчитаем примерный прогноз продаж нашей новинки.
Метод довольно грубый и не очень точный, однако при прогнозировании новинки с большим перечнем свойств, может очень сильно помочь. И да, телевизор — не совсем удачный продукт, так как он не является регулярным или с ярко-выраженной сезонностью, да и к тому же можно их всегда закупить побольше, так как у них нет таких сроков годности, как у пищевой продукции. Однако, именно как пример — он очень подходит, потому что максимально легок для восприятия.
Методы прогнозирования: итоги и полезные ссылки.
Здесь были рассмотрены самые распространенные и наиболее простые способы/методы прогнозирования. Помимо них существует еще и другие, в том числе и более сложные, например:
- Модели на основе авторегрессии и среднего скользящего (ARIMA или модель Бокса-Дженкинса, ARIMAX и SARIMA)
- Модели на основе нейронных сетей (построение прогноза с помощью искусственного интеллекта)
- Прогнозирование с помощью «бутстреппинга»
- И другие модели/способы/методы прогнозирования
Возможно, спустя какое-то время, по некоторым из них будут написаны отдельные статьи (либо будет расширена текущая).
Файл с примерами расчетов в Excel, можно скачать нажав на кнопку ниже:
Так как статья про методы прогнозирования получилась довольно большой, информация про «Обработку прогноза» вынесена в отдельную статью: «Прогнозирование, шаг 6.2: обработка прогноза».
Если вы хотите больше узнать больше информации по прогнозированию, изучить более сложные модели и методы прогнозирования, то вам могут пригодиться следующие ссылки:
Видео:Excel. Линия трендаСкачать

О линейном тренде
Автор: Алексей Батурин.
Из данного материалы вы узнаете, что важно знать о линейном тренде для прогнозирования :
Линейный тренд разложим на «запчасти»;
Как скорректировать значения линейного тренда и для чего;
Линейный тренд – это функция y=ax+b, где
Значение x – это номер периода во временном ряду (например, номер месяца, квартала, дня; См. статью о временных рядах.)
y – это последовательность значений , которые мы анализируем (например, продажи по месяцам.)
b – точка пересечения с осью y на графике (минимальный уровень);
a – это значение, на которое увеличивается следующее значение временного ряда;
Причем, если a>0, то динамика роста положительная,
по 28-й — y=53934*28+1784066 = 3294218
Получили прогнозные значения тренда с 15 по 28 месяца. Отношение прогноза к фактическим данным 1,34, т.е. прогнозируется рост на 34%.
Как мы можем скорректировать прогнозные значения тренда?
Если нас рост не устраивает, т.е. мы понимаем, что есть факторы, которые на него повлияют, мы можем скорректировать тренд.
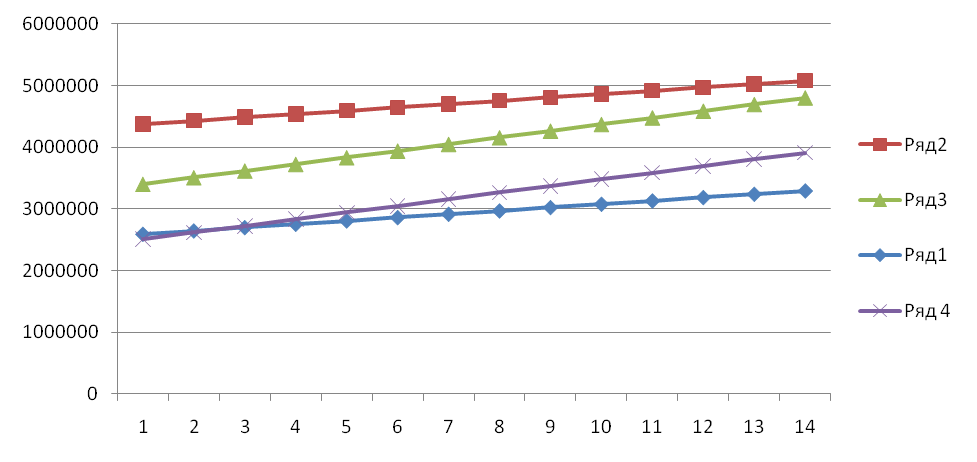
Скорректируем значение рассчитанного нами выше тренда y=53934x+1784066 – ряд 1 на графике:
Если изменяем значение «a» линейного тренда y=ax+b, то увеличиваем наклон тренда (ряд 3 на графике);
Если изменяем значение «b» линейного тренда (Ряд 2), то тренд мы поднимаем параллельно ряду 1.
Т.е. мы можем изменять наклон тренда, изменять уровень тренда, и одновременно и уровень и наклон — ряд 4 (пример во вложении).
Теперь рассчитаем коэффициенты сезонности с помощью Forecast4AC PRO (лист «ForLin»). Умножим значения тренда на сезонность. Прогноз продаж готов! Также стоит учесть дополнительные факторы, кроме сезонности, которые влияют на объем продаж.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Видео:Прогнозирование в Excel с помощью линий трендаСкачать

Анализ временных рядов, тренд ряда динамики, точечная оценка прогноза
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 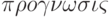
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 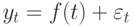

Неслучайная функция f (t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами ( t, yt ) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t ), где f (t) = a0+a1(t ).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel .
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f (t) в точках ti от значений исходного временного ряда в тех же точках ti . Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид 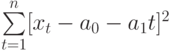
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
| t | t 2 | хt | хtt |
|---|---|---|---|
| 1 | 1 | 2 | 2 |
| 2 | 4 | 1 | 2 |
| 3 | 9 | 4 | 12 |
| 4 | 16 | 4 | 16 |
| 5 | 25 | 6 | 30 |
| 6 | 36 | 8 | 48 |
| 7 | 49 | 7 | 49 |
| 8 | 64 | 9 | 72 |
| 9 | 81 | 12 | 108 |
| 10 | 100 | 11 | 110 |
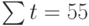 | 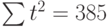 | 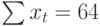 | 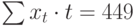 |
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f (t) имеет вид:
f (t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Временной ряд приведен в таблице. Используя средства MS Excel :
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Рассмотрим решение этой задачи средствами Microsoft Excel . При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3 рис. 14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4 рис. 14.4.
Итоговый график представлен на рисунке 14.5 рис. 14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t ), найденного по методу наименьших квадратов. Для этого в полученное для f (t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel ):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t ), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
📹 Видео
Лабораторная работа Прогнозирование по уравнению трендаСкачать

Excel для полных чайников Урок 16 Линия трендаСкачать
Быстрое прогнозирование в Microsoft ExcelСкачать
Модели статистического прогнозирования | Информатика 10-11 класс #35 | ИнфоурокСкачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

Парная регрессия: линейная зависимостьСкачать

Эконометрика. Линейная парная регрессияСкачать

Множественная регрессия в ExcelСкачать

Множественная регрессияСкачать

работа с уравнением линии тренда ExcelСкачать

Прогнозирование на основе построения модели линейного тренда в MS ExcelСкачать

Аналитическое выравниваниеСкачать

Уроки Excel. Статистические функции. Линия Тренда.Скачать

Временные ряды и прогнозированиеСкачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Прогнозирование с помощью инструментов MS Excel | ИРТС | Морозова ДарьяСкачать

1 8 Статистические методы прогнозированияСкачать

Решение задач в Microsoft Excel. Линии трендаСкачать