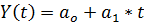Уравнение линейного тренда и оценка его значимости

Для оценки статистической значимости линейного тренда рассматриваемых климатических характеристик (температуры воздуха и атмосферных осадков) применяются следующие методы.

1. Метод, основанный на использовании коэффициента корреляции, учитывающего связи между значениями временного ряда (х_i) и их порядковыми номерами(i)

Коэффициент корреляции находится по формуле:

(6)

где; x_i – значение климатической характеристики рассматриваемого временного ряда (например, значение среднегодовой температуры воздуха);

x ̄ – среднемноголетнее значение климатических характеристики (например, климатическая норма среднегодовой температуры воздуха);

i – порядковый номер члена ряда;

– среднеарифметическое значение, полученное из порядковых номеров членов ряда, ;

– среднеквадратические отклонения значений временного ряда климатической характеристикии их порядковых номеров.

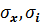
ü , — статистическая связь между двумя рядами признается слабой;

ü , — статистическая связь признаётся средней;

ü — высокая степень статистической связи.

Для временного ряда среднегодовой температуры воздуха для метеостанции Ростова-на-Дону

Коэффициент корреляции между значениями временного ряда среднегодовой температуры воздуха и их порядковыми номерами равен 0,6. А коэффициент корреляции между значениями годовых атмосферных осадков и их порядковыми номерами составляет

После определения коэффициента корреляции определяем среднеквадратическое отклонение коэффициента корреляции, которое рассчитывается по формуле:

(7)

Далее производим расчёт коэффициента достоверности коэффициента корреляции, который рассчитывается по формуле:

(8)

Если и , то при 5%–ном уровне значимости критерия ( коэффициент корреляции достоверен, и линейный тренд рассматриваемой климатической характеристики статистически значим и отличается от нуля.

Уровень значимости, равный 5% означает, что в 5 случаях из 100 мы будем ошибочно отвергать гипотезу о наличии тренда.

Расчёты для временных рядов среднегодовой и сезонной температуры воздуха и суммарных атмосферных осадков для метеостанции Ростова-на-Дону за период 1881-2012 гг. выполнены при помощи пакета прикладных программ «Microsoft Excel». Результаты расчетов приведены в таблице 3.5. Как видно из таблицыкоэффициент корреляции достоверен для годовой и сезонной температуры воздуха, и следовательно рассматриваемые линейные тренды климатических характеристик статистически значимы, имеет место линейный тренд. А для атмосферных осадков, как показывает коэффициент корреляции, линейный тренд не достоверен как для годового периода, так и для выделенных сезонов.

Таблица 3.5 — Оценка линейного тренда климатических характеристик для метеостанции Ростова-на-Дону за период 1881-2012 гг.

Оценка значимости тренда по коэффициенту корреляции

Оценка значимости тренда по коэффициенту корреляции

r 2 К_Dr 2 К_D1) Среднегодовая температура воздуха0,60,060,018103) Годовые атмосферные осадки-0,080,0150,03-0,522) Температура воздуха по сезонам года:4) Количество осадков по сезонам года:Зима0,40,070,145,28Зима0,090,150,030,59Весна0,480,070,146,99Весна0,010,150,030,1Лето0,340,080,164,37Лето-0,010,150,03-0,07Осень0,250,080,163,03Осень0,030,150,030,19

2) Методика оценки статистической значимости линейного тренда климатических характеристик, основанная на методе И.И.Поляка.

Согласно данной методике рассчитывается уравнение линейной регрессии (тренда) следующего вида:

Дли принятия гипотезы о наличии линейного тренда по методике И.И. Поляка, требуется выполнение следующих условий:

1)

2) ,

где – дисперсия наблюденных величин от среднего значения; – дисперсия отклонения наблюденных величин от линии тренда, которая определяется по формуле

,

где r – коэффициент корреляции между наблюденной величиной и ее порядковым номером, – среднее квадратическое отклонение регрессионного коэффициента , которое определяется по формуле

Если два условия (1) и (2) выполняются, то линейный тренд климатической характеристики является значимым с вероятностью 5%; если выполняется лишь одно из условий или условия не выполняются вообще, то процесс изменения климатической характеристики является стационарным.

Результаты проведенных расчётов представлены в таблице 3.6. Как видно из таблицы, линейный тренд среднегодовой и сезонной температуры воздуха и атмосферных осадков для метеостанции Ростова-на-Дону за период 1881-2012 гг. является статистически незначимым с вероятностью 5%.

Таблица 3.6 — Оценка линейного тренда климатических характеристик по методу Поляка И.И. для метеостанции Ростова-на-Дону за период 1881-2012 гг.

Оценка значимости тренда по методу И.И. Поляка

О линейном тренде

Автор: Алексей Батурин.

Из данного материалы вы узнаете, что важно знать о линейном тренде для прогнозирования :

Линейный тренд разложим на «запчасти»;

Как скорректировать значения линейного тренда и для чего;

Линейный тренд – это функция y=ax+b, где

Значение x – это номер периода во временном ряду (например, номер месяца, квартала, дня; См. статью о временных рядах.)

y – это последовательность значений , которые мы анализируем (например, продажи по месяцам.)

b – точка пересечения с осью y на графике (минимальный уровень);

a – это значение, на которое увеличивается следующее значение временного ряда;

Причем, если a>0, то динамика роста положительная,

по 28-й — y=53934*28+1784066 = 3294218

Получили прогнозные значения тренда с 15 по 28 месяца. Отношение прогноза к фактическим данным 1,34, т.е. прогнозируется рост на 34%.

Как мы можем скорректировать прогнозные значения тренда?

Если нас рост не устраивает, т.е. мы понимаем, что есть факторы, которые на него повлияют, мы можем скорректировать тренд.

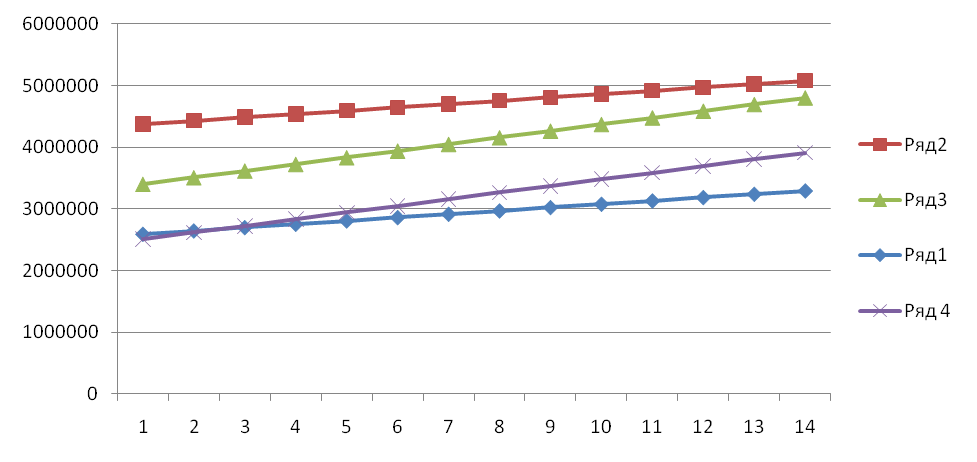
Скорректируем значение рассчитанного нами выше тренда y=53934x+1784066 – ряд 1 на графике:

Если изменяем значение «a» линейного тренда y=ax+b, то увеличиваем наклон тренда (ряд 3 на графике);

Если изменяем значение «b» линейного тренда (Ряд 2), то тренд мы поднимаем параллельно ряду 1.

Т.е. мы можем изменять наклон тренда, изменять уровень тренда, и одновременно и уровень и наклон — ряд 4 (пример во вложении).

Теперь рассчитаем коэффициенты сезонности с помощью Forecast4AC PRO (лист «ForLin»). Умножим значения тренда на сезонность. Прогноз продаж готов! Также стоит учесть дополнительные факторы, кроме сезонности, которые влияют на объем продаж.

Точных вам прогнозов!

Присоединяйтесь к нам!

Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:

• Novo Forecast Lite — автоматический расчет прогноза в Excel .
• 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

• Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Тенденция во временном ряду

Синонимом тенденции в эконометрике является тренд. Одним из наиболее популярных способов моделирования тенденции временного ряда является нахождение аналитической функции, характеризующей зависимость уровней ряда от времени. Этот способ называется аналитическим выравниванием временного ряда.

Зависимость показателя от времени может принимать разные формы, поэтому находят различные функции: линейную, гиперболу, экспоненту, степенную функцию, полиномы различных степеней. Временной ряд исследуют аналогично линейной регрессии.

Параметры любого тренда можно определить обычным методом наименьших квадратов, используя в качестве фактора время t = 1, 2,…, n, а в качестве зависимой переменной используют уровни временного ряда. Для нелинейных трендов сначала проводят процедуру линеаризации.

К числу наиболее распространенных способов определения типа тенденции относят качественный анализ изучаемого ряда, построение и анализ графика зависимости уровней ряда от времени, расчет основных показателей динамики. В этих же целях можно часто используют и коэффициенты автокорреляции уровней временного ряда.

Линейный тренд

Тип тенденции определяют путем сравнения коэффициентов автокорреляции первого порядка. Если временной ряд имеет линейный тренд, то его соседние уровни yt и yt-1 тесно коррелируют. В таком случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть максимальный. Если временной ряд содержит нелинейную тенденцию, то чем сильнее выделена нелинейная тенденция во временном ряду, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить перебором основных видов тренда, расчета по каждому уравнению коэффициента корреляции и выбора уравнения тренда с максимальным значением коэффициента.

Параметры тренда

Наиболее простую интерпретацию имеют параметры экспоненциального и линейного трендов.

Параметры линейного тренда интерпретируют так: а — исходный уровень временного ряда в момент времени t = 0; b — средний за период абсолютный прирост уровней рада.

Параметры экспоненциального тренда имеют такую интерпретацию. Параметр а — это исходный уровень временного ряда в момент времени t = 0. Величина exp(b) — это средний в расчете на единицу времени коэффициент роста уровней ряда.

По аналогии с линейной моделью расчетные значения уровней рада по экспоненциальному тренду можно определить путем подстановки в уравнение тренда значений времени t = 1,2,…, n, либо в соответствии с интерпретацией параметров экспоненциального тренда: каждый последующий уровень такого ряда есть произведение предыдущего уровня на соответствующий коэффициент роста

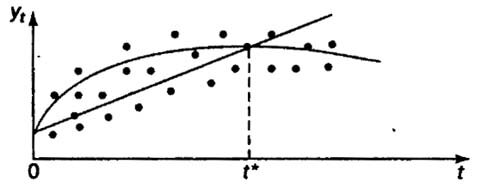
При наличии неявной нелинейной тенденции нужно дополнять описанные выше методы выбора лучшего уравнения тренда качественным анализом динамики изучаемого показателя, для того, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом ряду поворотных точек и изменения темпов прироста, начиная с определенного момента времени под влиянием ряда факторов, и т. д. В том случае если уравнение тренда выбрано неправильно при больших значениях t, результаты прогнозирования динамики временного ряда с использованием исследуемого уравнения будут недостоверными по причине ошибки спецификации.

Иллюстрация возможного появления ошибки спецификации приведем на рисунке

Если оптимальной формой тренда является парабола, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция естественно будут по разному описывать тенденцию в уровнях ряда.

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.

🔥 Видео