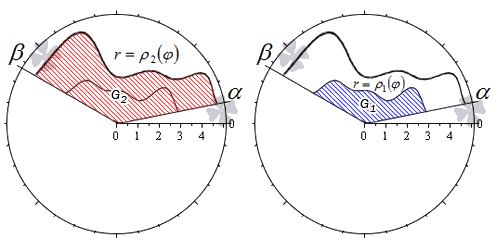Уравнение лемнискаты бернулли в полярных координатах

Видео:§3 Лемниската БернуллиСкачать

Уравнения кривых. Лемниската Бернулли.

Лемниската Бернулли — кривая, у которой произведение расстояний от каждой её точки до двух определенных точек (фокусов) неизменно и равняется квадрату половины расстояния между ними. Место пересечения лемнискаты с самой собой принято называть узловой или двойной точкой.

Форма лемнискаты похожа на восьмерку (символ бесконечности).

(х 2 + у 2 ) 2 = 2 а 2 (х 2 — у 2 ).

Полярное уравнение имеет вид:

Длина дуги лемнискаты между точками, для которых φ₁= 0 и φ₂= φ:

.

Площадь сектора ограниченного осью и радиус-вектором, соответствующим углу φ:

Площадь, локализованную лемнискатой:

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Построение графика неявно заданной функции на примере лемнискаты Бернулли

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Тема: «Построение графика неявно заданной функции на примере лемнискаты Бернулли»

Проект
Гузь Ольги

Содержание.
1.Определение функции заданной неявно.
2.Определение лемнискаты.
3.Вывод уравнения лемнискаты.
4.Преобразование уравнения лемнискаты.
5.Уравнение лемнискаты в полярной системе координат.
6.Исследование уравнения лемнискаты.
7.Построение лемнискаты.
8. Применение лемнискаты.
9.Краткая историческая справка.

Определение неявно заданной функции
Рассмотрим функцию, заданную неявно уравнением F(x ,y)=0.
В зависимости от того, какой является функция F(x ,y)-алгебраической или трансцендентной,- кривые также делятся на алгебраические и трансцендентные.
Примеры, лемниската Бернулли.

Лемниската –
это кривая, у которой произведение расстояний каждой ее точки до двух заданных точек- фокусов -постоянно и равно квадрату половины расстояния между ними.

Пусть фокусы имеют координаты: F1(-a;0) и F2 (а;0); М(х, у) — произвольная точка геометрического места,
то по условию

Подставляя в это равенство выражения

получим искомое уравнение данного геометрического места

Вывод уравнения лемнискаты

Преобразование уравнения лемнискаты

Дальнейшая цель- получить уравнение лемнискаты Бернулли в более простом виде.
Возводя в квадрат обе части уравнения и группируя члены, находим

Преобразование уравнения лемнискаты
Преобразуя последнее уравнение, имеем:

или в окончательном виде

Мы получили уравнение лемнискаты в декартовой системе координат.

Построение графика лемнискаты

Т.к х и у входят в это уравнение только в чётных степенях, то лемниската симметрична относительно координатных осей.
Построить график данной функции затруднительно.
Запишем это же уравнение в полярной системе координат.

Уравнение лемнискаты в полярной системе координат

Поскольку х =ρ cos φ, у = ρ sinφ, х2+у2= ρ2, то уравнение лемнискаты в полярных координатах примет вид
ρ 4=2а2 ρ(cos2φ- sin2φ)
или

ρ 2=2а2 cos2φ
Из этого уравнения видно, что
при φ=0. Если φ увеличивается в пределах
от 0 до , то ρ уменьшается от до ρ=0.
Если , то ρ принимает мнимые
значения. Это означает, что на лемнискате нет точек, для которых φ меняется в указанных пределах.
Исследование уравнения лемнискаты

Построение лемнискаты
Построим график функции
при разных значениях а:

Построение лемнискаты
при а=-0,5

При построении кривых семейства овалов Кассини, промежуточным графиком является лемниската Бернулли.

1. 2. 3. 4.
Фигура выпуклая как эллипс.
Появляется вогнутая перемычка с четырьмя точками перегиба.
Перемычка смыкается, полученная фигура называется лемнискатой Бернулли.
Фигура разваливается на два овала.

В технике лемниската применяется, в частности, в качестве переходной кривой на закруглениях малого радиуса, как это имеет место на железнодорожных линиях в горной местности и на трамвайных путях.
Применение:

Существует два способа построения лемнискаты.
Первый способ — с помощью
двух угольников и нарисованной на листе бумаги окружности (рис.2).Вершина острого угла одного из угольников находится в центре окружности, вершина прямого угла другого -на окружности.
Способы построения лемнискаты
Рис.2

Второй способ — с помощью шарнирного устройства, две точки которого закреплены на плоскости (рис.3).
Способы построения лемнискаты
Рис.3

Лемниската Бернулли.
Ее автор – швейцарский математик Якоб Бернулли. Он дал этой кривой поэтическое название «лемниската».

В античном Риме так называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх.

БЕРНУЛЛИ Якоб I (1654-1705). Швейцарский математик. Работал в Базельском университете.
Работы посвящены математическому анализу, теории вероятностей и механике. В 1687 познакомился с первым мемуаром Лейбница по дифференциальному исчислению и применил его идеи к изучению ряда кривых, встречающихся в математике, механике, и выводу формулы радиуса кривизны плоской кривой. Ввел термин «интеграл».
Краткая биография

♣ Вирченко Н.А. и др.Справочник «Графики функций»; Киев: Наук. думка, 1979г;
♣ И.И.Валуцэ «Математика для техникумов»; Москва, Издательство «Наука», 1980г;
♣ Маркушевич А.И. «Замечательные кривые»; Москва 1978 г.
Список использованной литературы

Internet-ресурсы: WWW.Colledg.Ru;
WWW.5ballov.Ru; WWW.bankreferatov.Ru; WWW.rubricon.com.
Программное обеспечение: MS Word; MS Power Point;Windows Media; Nero Wave Editor; Сканер.

Список использованной литературы

Курс повышения квалификации

Охрана труда

• Сейчас обучается 120 человек из 43 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 236 человек из 54 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 354 человека из 64 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Лемниската Бернулли: площадь "бесконечности"Скачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 588 831 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 28.12.2020
• 937
• 13

• 28.12.2020
• 999
• 0

• 28.12.2020
• 1170
• 0

• 28.12.2020
• 1279
• 1

• 28.12.2020
• 1794
• 4

• 28.12.2020
• 1227
• 0

• 28.12.2020
• 1289
• 0

• 23.12.2020
• 1329
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 10.07.2020 788
• PPTX 1.1 мбайт
• 3 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Якимова Светлана Семеновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 1 месяц
• Подписчики: 0
• Всего просмотров: 28417
• Всего материалов: 247

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Лемниската БернуллиСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Каждый второй ребенок в школе подвергался психической агрессии

Время чтения: 3 минуты

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Только 23 февраля!
Получите новую
специальность
по низкой цене

Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

Видео:Длина лемнискаты Бернулли и эллиптический интегралСкачать

Вычисление площади фигуры в полярных координатах

В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.

Видео:Скорость и ускорение точки в полярных координатахСкачать

Краткий обзор статьи

• Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
• Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
• В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.

Видео:Полярная система координатСкачать

Полярная система координат и криволинейный сектор

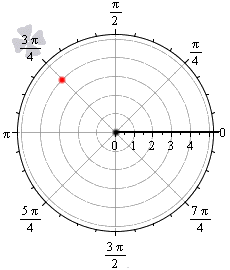
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 — это расстояние от заданной точки до начала координат.

На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .

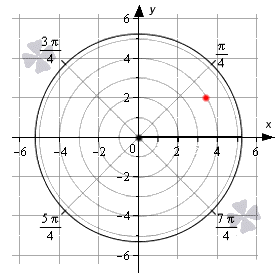
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.

Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .

Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .

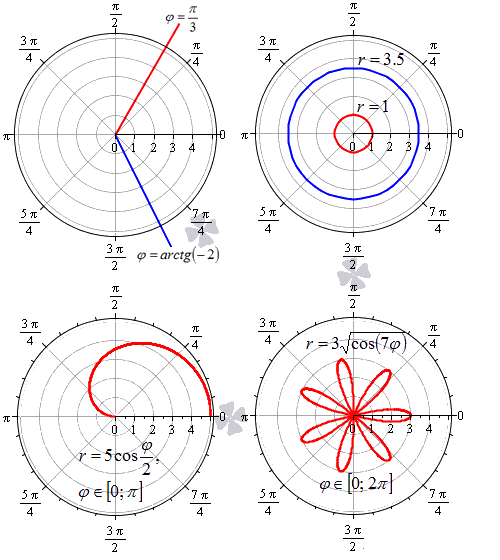
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где — это радиус.

Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.

Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.

На рисунке мы изобразили несколько примеров линий в полярной системе координат.

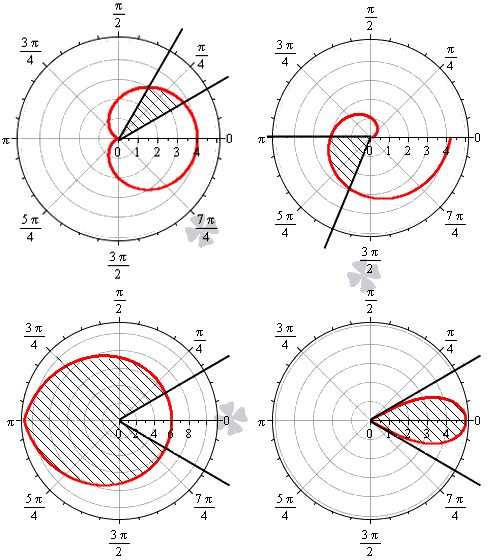
Дадим определение криволинейному сектору.

Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .

На рисунке мы привели несколько примеров криволинейных секторов.

На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = — π 6 , φ = π 6 , которые не являются ее границами.

Видео:Построение кривой в полярной системе координатСкачать

Площадь криволинейного сектора — вывод формулы

Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.

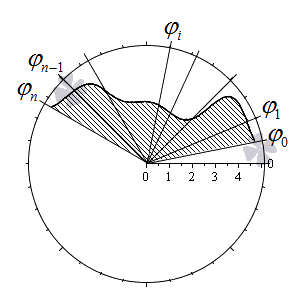
Разобьем криволинейный сектор на n частей такими лучами

φ = φ 1 , φ = φ 2 , . . . , φ = φ n — 1 , что α = φ 0 φ 1 φ 2 . . . φ n — 1 β и λ = m a x i = 1 , 2 , . . . , n φ i — φ i — 1 → 0 при n → + ∞ .

Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:

S ( G ) = ∑ i = 1 n S ( G i )

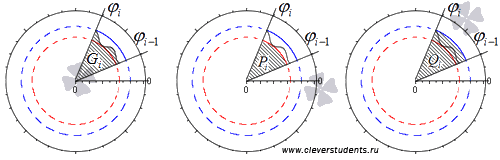
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i — 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.

Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.

Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i — φ i — 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .

Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:

lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i — φ i — 1 = 1 2 ∫ β α p 2 φ d φ

Формула для определения площади криволинейного сектора имеет вид:

S ( G ) = 1 2 ∫ β α p 2 φ d φ

Видео:Лемниската БернуллиСкачать

Примеры вычисления площади криволинейного сектора

Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.

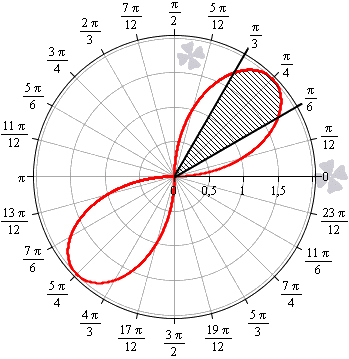
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .

Решение

Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .

Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.

S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 — cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 — cos ( 4 φ ) ) d φ = φ — 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 — 1 4 sin 4 π 3 — π 6 — 1 4 sin 4 π 6 = π 6 + 3 4

Ответ: S ( G ) = π 6 + 3 4

Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.

Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.

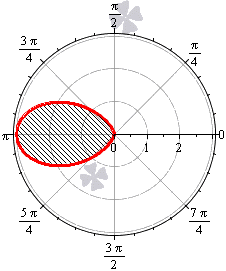
Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = — 3 · cos 3 φ .

Решение

Функция определена для всех действительных значений аргумента. Решим неравенство — 3 · cos 3 φ ≥ 0 :

— 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z

Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.

Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .

S ( G ) = 1 2 ∫ π 2 3 π 2 ( — 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ

Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n — 1 ( x ) n + n — 1 n K n — 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .

∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 — 15 48 · π 2 = 5 π 16

Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .

Ответ: S ( G ) = 45 π 32

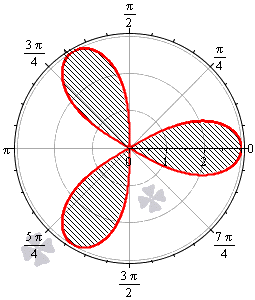
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.

Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .

Решение

Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.

cos ( 3 φ ) ≥ 0 ⇔ — π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z — π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z

Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.

Построим фигуру на графике.

Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):

1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 — sin 3 · π 2 = 3 2 ( 1 — ( — 1 ) = 3

Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.

Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.

Видео:Видеоурок "Полярная система координат"Скачать

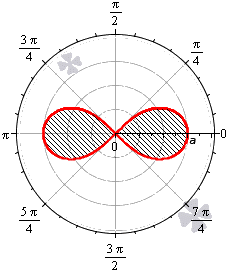
Площадь фигуры, которую ограничивает лемниската Бернулли

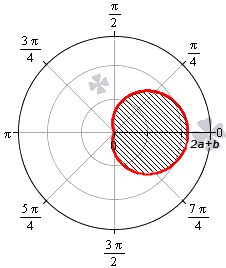
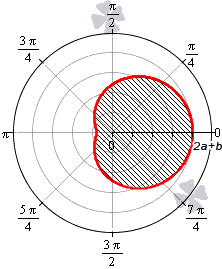
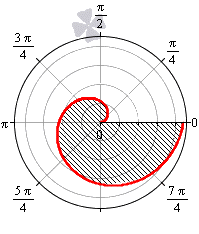
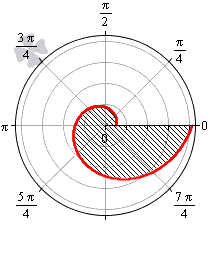
Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при — π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .

Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.

Для вычисления площади используем нужную формулу:

S ( G ) = 2 · 1 2 ∫ — π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) — π 4 π 4 = = a 2 2 sin 2 · π 4 — sin 2 · — π 4 = a 2

Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .

Видео:Оператор Лапласа в полярных координатахСкачать

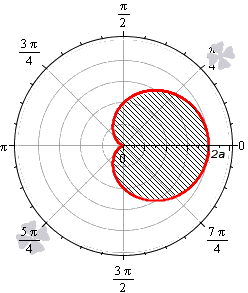
Площадь фигуры, границей которой является кардиоида

В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.

Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :

S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2

Видео:Линии в полярных координатах и параметрически заданныеСкачать

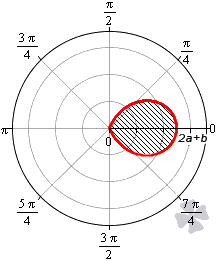
Площадь фигуры, которую ограничивает улитка Паскаля

В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .

Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.

При b — 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .

При b = — 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.

При — 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z .

При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.

При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже

Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .

Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = — 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.

Решение

Формула r = — 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..

Функция r = — 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:

— 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ — π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z

Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:

S ( G ) = 1 2 ∫ — π 3 π 3 ( — 3 + 6 cos φ ) 2 d φ = 9 2 ∫ — π 3 π 3 ( 1 — 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ — π 3 π 3 1 — 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ — π 3 π 3 ( 3 — 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ — 4 sin φ + sin ( 2 φ — π 3 π 3 = = 9 2 · 3 · π 3 — 4 sin π 3 + sin 2 π 3 — 3 · — π 3 — 4 sin — π 3 + sin — 2 π 3 = = 9 2 · 2 π — 3 3

Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:

S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) — 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π

Ответ: S ( G ) = 33 π

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль

Сразу обратимся к примеру.

Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .

Решение

Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.

Исходя из этого, найдем площадь фигуры по формуле:

S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3

Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:

S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π — 1

Видео:§30 Уравнения кривых второго порядка в полярных координатахСкачать

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов

Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .

Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ .

Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .

Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:

S ( G ) = S ( G 2 ) — S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ — 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ

Последний переход возможен в силу третьего свойства определенного интеграла.

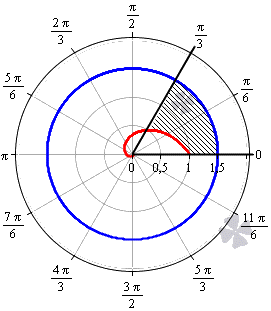
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.

Решение

Построим заданную фигуру на графике.

Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:

S ( G ) = 1 2 ∫ 0 π 3 3 2 2 — 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 — 2 — 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 — 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 — 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

Ответ: S ( G ) = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.

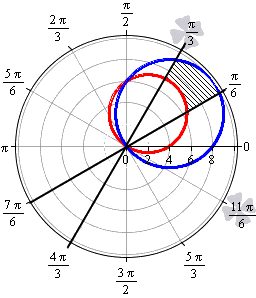
Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x — 2 ) 2 + ( y — 3 ) 2 = 13 , ( x — 4 ) 2 + ( y — 3 ) 2 = 25 .

Решение

В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.

x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x — 2 ) 2 + ( y — 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x — 4 ) 2 + ( y — 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ

Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:

S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 — 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 — π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 — sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 — 1 2 2 = 2 π + 6

🎬 Видео

Лемниската БернуллиСкачать

Полярная система координатСкачать

Двойной интеграл в полярных координатахСкачать

Построение графика функции в полярных координатахСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Лемниската (lemniscate)Скачать