Пусть две дифракционные решетки поставлены одна за другой так, что их штрихи взаимно перпендикулярны. Такая пластинка представляет собой двумерную периодическую структуру.
Рис. 5.11.1 Двумерная периодическая структура
Дифракция наблюдается также на трехмерных структурах, т. е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами являются все кристаллические тела. Однако период их (


Найдем условия образования дифракционных максимумов от трехмерной структуры. Проведем в направлениях, по которым свойства структуры обнаруживают периодичность, координатные оси x, y, z (рис. 5.11.1). Структуру можно представить как совокупность равноотстоящих параллельных линейных цепочек из структурных элементов, расположенных вдоль одной из координатных осей . Рассмотрим действие отдельной линейной цепочки , параллельной , например , оси х (рис. 5.11.2). Пусть на нее падает пучок параллельных лучей , образующих с осью х угол 




Рис. 5.11.2 Дифракция рентгеновских лучей
Под действием рентгеновского излучения каждый атом кристаллической решетки становится источником сферических волн той же частоты, что и падающих волн.
Запишем условия Лауэ 




Уравнения носят название формул Лауэ. Каждому определяемому этими уравнениями направлению(



Русский ученый Ю. В. Вульф и английские физики У. Г. и У. Л. Брэгги показали независимо друг от друга, что расчет дифракционной картины от кристаллической решетки можно провести также следующим простым способом.
Видео:2.1 Дифракция рентгеновских лучей и обратная решёткаСкачать

Формула Брега-Вульфа
Рис. 5.11.3 Формула Брега-Вульфа
Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости (рис.5.11.3.). В дальнейшем мы будем называть их атомными слоями. Если падающая на кристалл волна плоская, огибающая вторичных волн, порождаемых атомами, лежащими в таком слое, также будет представлять собой плоскость. Таким образом, суммарное действие атомов, лежащих в одном слое, можно представить в виде плоской волны, отразившейся от усеянной атомами поверхности по обычным законам отражения. Плоские вторичные волны, отразившиеся от разных атомных слоев, когерентны и будут интерферировать между собой подобно волнам, посылаемым в данном направлении различными щелями дифракционной решетки. При этом, как и в случае решетки, вторичные волны будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода между соседними волнами является кратной 


Соотношение называется формулой Вульфа — Брэгга.
Заметим, что расчет по формулам Лауэ и расчет по формуле Вульфа — Брэгга приводят к совпадающим результатам.
Видео:Консультация к ГКЭ. Оптика. "Дифракция рентгеновских лучей"Скачать

ВВЕДЕНИЕ
Физические свойства твердых тел определяются их внутренним микроскопическим строением. Это строение обусловлено взаимным расположением структурных частиц вещества (атомов, молекул, ионов) из которых состоит твердое тело. В зависимости от степени упорядоченности атомов твердые тела разбиваются на два типа: аморфные и кристаллические. Для аморфного состояния характерна упорядоченность на расстояниях сравнимых с межатомными. В кристаллах правильное чередование атомов наблюдается на неограниченно больших расстояниях, т.е. наряду с ближним порядком, существует и дальний порядок. Основным признаком дальнего порядка является симметрия кристалла. В реальных кристаллических телах всегда существуют в большей или меньшей степени микро- или макро-нарушения порядка, которые, так или иначе, сказываются на его свойствах.
Упорядоченное строение кристаллических твердых тел впервые было доказано в 1912 году М. Лауэ с помощью дифракции рентгеновских лучей. Кристаллы являются природными дифракционными решетками для этих лучей, поскольку длины волн рентгеновских лучей соизмеримы с межатомными расстояниями в кристаллических структурах. Излучения с большей длиной волны не могут выявить деталей структуры на атомном уровне, а коротковолновое излучение дифрагирует, отклоняясь лишь на очень малые углы, что весьма неудобно. В настоящее время существуют несколько дифракционных методов исследования атомного строения вещества: рентгено-, электроно- и нейтронографический методы. Различие этих методов вытекает из особенностей взаимодействия данных излучений с веществом. Общим у этих трех методов является то, что они опираются на общую теорию упругого рассеяния.
УСЛОВИЯ НАБЛЮДЕНИЯ ДИФРАКЦИОННЫХ МАКСИМУМОВ
Для того, чтобы волны, рассеянные семейством параллельных плоскостей кристалла дали максимум интенсивности необходимо выполнение следующего соотношения между межплоскостным расстоянием d , углом падения рентгеновских волн на данную кристаллографическую плоскость и длиной волны рентгеновского излучения l :
здесь n – любое целое число (порядок отражения).
Это равенство выражает основной закон дифракции рентгеновских лучей в кристаллах и называется условием Брэгга-Вульфа.
Это условие имеет простую физическую интерпретацию: рентгеновские волны, рассеянные соседними атомными плоскостями кристалла будут при интерференции усиливаться в том случае, когда разность хода между ними равна целому числу длин волн λ .
Брэгговское отражение имеет место только при длинах волн λ ≤ 2 d . С уменьшением λ уменьшается и угол θ .
Часто для нахождения условий усиления рассеянных кристаллической решеткой волн используют эквивалентные уравнению Брэгга-Вульфа условия Лауэ. Для вывода условий Лауэ необходимо рассмотреть результат интерференции волн, рассеянных от соседних атомов кристаллической решетки. Для одномерной цепочки атомов с межатомным расстоянием а в случае перпендикулярного падения первичных волн относительно линии атомов условие усиления запишется в виде:

здесь m – любое целое число, j — угол между линией атомов и направлением рассеяния.
Для трехмерной решетки атомов необходимо одновременное выполнение трех условий:



В этих формулах a , b , c – параметры решетки; j a , j b , j c – углы рассеяния вдоль соответствующих кристаллографических направлений; h , k , l – любые целые числа, определяющие порядок спектра.
АМПЛИТУДЫ РАССЕЯННЫХ ВОЛН.
Условия (2) и (3) дают возможность определить только направления, при которых происходит усиление рентгеновских волн, рассеянных атомными плоскостями или атомами кристалла. Интенсивность дифрагированного луча определяется электронной плотностью атомов, расположением атомов в элементарной ячейке, тепловыми колебаниями атомов кристаллической решетки и т.д.
Наиболее простой метод расчета интенсивности дифракционных максимумов, предложенный Лауэ, состоит в суммировании вкладов от элементарных волн, рассеянных от каждого элемента кристалла.
Выражение для суммарного рассеяния в направлении к точке наблюдения от решетки точечных атомов можно получить, суммируя амплитуды рассеянных волн по всем точкам решетки. Интересующая нас величина является суммой фазовых множителей:

где m, n, p — целые числа, принимающие значения от 0 до Н (в этом случае кристалл содержит Н 3 примитивных ячеек), ρ mnp — вектор, который проводится из начала системы координат, и принимает все возможные значения в соответствии с выражением:
a , b и c — единичные векторы, q — вектор рассеяния.
Пусть в кристалле конечных размеров, имеющем форму параллелепипеда, одинаковые точечные центры рассеяния расположены в каждом узле решетки ρmnp . Из (3) видно, что величина суммарного излучения пропорциональна


Величину I называют амплитудой рассеяния
Сумма, взятая по узлам решетки максимальна когда:

для всех узлов решетки, т. к. каждый член, имеющий форму exp(- i ρ mnp q ) , равен единице. Когда q удовлетворяет выражению (5), сумма для амплитуды рассеяния в пределах кристалла, имеющего Н 3 узлов решетки, дает:
Отклонение значения q от величины, удовлетворяющей соотношению (5), будет значительно уменьшать величину суммы в (4).
Величина q удовлетворяет условию дифракции (5), если выполняются одновременно следующие три условия для целых чисел h , k , l :
Эти уравнения называются уравнениями дифракции Лауэ.
Также как и формула Брэгга-Вульфа (1), уравнения Лауэ представляют собой необходимые условия дифракции. Если элементарная кристаллическая ячейка содержит более одного атома, то эти уравнения не являются достаточными условиями, так как необходимо также, чтобы структурный фактор (определение его дано ниже) не был равен нулю. Если он равен нулю, то амплитуда рассеянной волны будет равна нулю.
При рассеянии рентгеновских лучей основную роль играют электроны атомов, т.к. масса ядра слишком велика, чтобы «почувствовать» рентгеновский квант. Интенсивность различных отражений зависит от состава элементарной ячейки, т.е. от числа и расположения атомов в ячейке и от распределения их электронной плотности. Наиболее типичным случаем рассеяния является рассеяние на распределении электронной плотности по всему кристаллу. Если рассеяние на элементе объема кристалла dV пропорционально локальной электронной плотности (концентрации электронов) n (ρ) , то амплитуда рассеяния пропорциональна интегралу:

Как известно, электроны в атоме не концентрируются вблизи ядра, а располагаются в его окрестности.
Распределение электронов в кристалле можно описать с помощью суперпозиции функций электронной
плотности Cj ,каждая из которых связана с отдельным атомом. Так, функция

определяет концентрацию электронов в точке ρ вблизи j -го атома ячейки mnp . Допустим, что каждая ячейка состоит из s атомов. Тогда полная электронная плотность n (ρ) в кристалле может быть записана в виде суммы:

где первое суммирование ( j =1,…, s ) производится по всем атомам базиса, а второе по всем узлам решетки, число которых, определенное выше равно Н 3 .
В соответствии с (7) общую амплитуду рассеяния в кристалле для вектора рассеяния q можно записать:

Вклад в I единичного члена C j (ρ- ρi— ρmnp) в выражении (10) равен:

где 

называется атомным фактором рассеяния или форм-фактором. Величина fj является мерой рассеивающей способности j -го атома элементарной ячейки. Она зависит от числа и распределения электронов атома, а также от длины волны и угла рассеяния излучения, вследствие интерференционных эффектов, обусловленных конечным размером атомов.
Выражение для амплитуды рассеяния можно теперь записать так:


При записи последнего выражения использовали полученный выше результат [см. форм. (5)], что 

называется структурным фактором базиса. Учитывая, что для некоторого отражения ( hkl ):

структурный фактор для указанного отражения можно записать:

Структурный фактор не обязательно должен быть вещественной величиной; в значение интенсивности рассеянной волны входит FF * , Где F * -величина, комплексно-сопряженная F .
ДИФРАКЦИЯ НА СВЕРХРЕШЕТКАХ.
Дифракция рентгеновского излучения хорошо подходит для изучения структуры сверхрешеток. Это неразрушающая методика и позволяет получать информацию на атомном уровне. Профиль рентгеновской дифракции обычно разделяется на 2 области — низкоугловую ( и высокоугловую (>15˚). Низкоугловая область возникает из-за дополнительного рассеяния слоями сверхрешетки, состоящих из различных химических элементов (материалов). В этой области позиции пиков определяются выражением:

где θ — угол положения пика, n -порядок отражения, λх— длина волны рентгеновского излучения, 

Для удобства, высокоугловые пики определяются относительно среднего значения постоянной решетки 

где n-целое число, указывающее номер (порядок) саттелитного пика вокруг основного Брэгговского пика и 
На интенсивность и вид высокоугловых пиков рентгеновского рассеяния значительно влияет беспорядок, присутствующий в структуре сверхрешетки. Различают дискретный и непрерывный совокупный беспорядок. Дискретный беспорядок толщины предполагает, что толщины изменяются целым числом атомных плоскостей. Непрерывный беспорядок относится к структурным параметрам,
На интенсивность и вид высокоугловых пиков рентгеновского рассеяния значительно влияет беспорядок, присутствующий в структуре сверхрешетки. Различают дискретный и непрерывный совокупный беспорядок.
Дискретный порядок толщины предполагает, что толщины изменяются целым числом атомных плоскостей. Непрерывный беспорядок относится к структурным параметрам, которые изменяются непрерывным образом подобно толщине аморфного слоя. Непрерывный беспорядок может быть разделен на два типа: внутрислойный и межслойный беспорядок.
Внутрислойный беспорядок относится к качеству упорядочения атомов в пределах одного слоя. Кристаллический слой имеет высокую степень внутрислойного порядка, в то время как аморфный слой не упорядочен.
Межслойный беспорядок относится к отклонениям в периодичности слоев в направлении роста, следующим из изменений толщины слоя и беспорядка «прослойки».
Общая модель сверхрешетки состоит из «пакета», содержащего М двойных слоев материалов А и В, показанного на рис. 1. Слои характеризуются структурными факторами FAj и FBj и толщинами tAj и tBj , материалов А и В, в j -ом двойном слое. Эта одномерная модель сверхрешетки явно включает только беспорядок промежуточного слоя.
Одномерный структурный фактор для сверхрешетки, состоящей из М двойных слоев с совокупными колебаниями толщины слоя:

Видео:Дифракция рентгеновских волн. Лекция 16-1Скачать
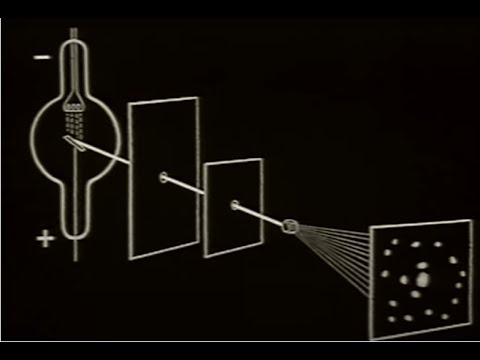
Электронный справочник: Дифракция рентгеновских лучей
Дифракция рентгеновских лучей рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта. Дифрагированные пучки составляют часть всего рассеянного веществом рентгеновского излучения. Наряду с рассеянием без изменения длины волны наблюдается рассеяние с изменением длины волны — так называемое комптоновское рассеяние (см. Комптона эффект). Явление Д. р. л., доказывающее их волновую природу, впервые было экспериментально обнаружено на кристаллах немецкими физиками М. Лауэ, В. Фридрихом и П. Книппингом в 1912.
Кристалл является естественной трёхмерной дифракционной решёткой для рентгеновских лучей, т.к. расстояние между рассеивающими центрами (атомами) в кристалле одного порядка с длиной волны рентгеновских лучей (
1Å=10 -8 см). Д. р. л. на кристаллах можно рассматривать как избирательное отражение рентгеновских лучей от систем атомных плоскостей кристаллической решётки (см. Брэгга — Вульфа условие). Направление дифракционных максимумов удовлетворяет одновременно трём условиям:
Здесь а, b, с — периоды кристаллической решётки по трём её осям; a0, b0, g0 — углы, образуемые падающим, а a, b, g — рассеянным лучами с осями кристалла; l — длина волны рентгеновских лучей, Н, К, L — целые числа. Эти уравнения называются уравнениями Лауэ. Дифракционную картину получают либо от неподвижного кристалла с помощью рентгеновского излучения со сплошным спектром (так называемая лауэграмма; рис. 1), либо от вращающегося или колеблющегося кристалла (углы a0, b0 меняются, а g0 остаётся постоянным), освещаемого монохроматическим рентгеновским излучением (l — постоянно), либо от поликристалла, освещаемого монохроматическим излучением. В последнем случае, благодаря тому что отдельные кристаллы в образце ориентированы произвольно, меняются углы a0, b0, g0.
Интенсивность дифрагированного луча зависит в первую очередь от так называемого структурного фактора, который определяется атомными факторами атомов кристалла, их расположением внутри элементарной ячейки кристалла, а также характером тепловых колебаний атомов. Структурный фактор зависит от симметрии расположения атомов в элементарной ячейке. Интенсивность дифрагированного луча зависит также от размеров и формы объекта, от совершенства кристалла и прочего.
Д. р. л. от поликристаллических тел приводит к возникновению резко выраженных конусов вторичных лучей. Осью конуса является первичный луч, а угол раствора конуса равен 4J (J — угол между отражающей плоскостью и падающим лучом). Каждый конус соответствует определённому семейству кристаллических плоскостей. В создании конуса участвуют все кристаллики, семейство плоскостей которых расположено под углом J к падающему лучу. Если кристаллики малы и их приходится очень большое количество на единицу объёма, то конус лучей будет сплошным. В случае текстуры, т. е. наличия предпочтительной ориентировки кристалликов, дифракционная картина (рентгенограмма) будет состоять из неравномерно зачернённых колец (см. также Дебая — Шеррера метод).
Метод Д. р. л. на кристаллах дал возможность определять длину волны рентгеновских лучей, если известна структура кристаллической решётки, благодаря чему возникла рентгеновская спектроскопия, сыгравшая важную роль при установлении строения атома. Наблюдения Д. р. л. известной длины волны на кристалле неизвестной структуры позволяют установить характер этой структуры (расположение ионов, атомов и молекул, составляющих кристалл), что послужило основой рентгеновского структурного анализа.
Д. р. л. наблюдается также при рассеянии их аморфными твёрдыми телами, жидкостями и газами. В этом случае на кривой зависимости интенсивности от угла рассеяния вокруг центрального пятна появляются широкие кольца типа гало (рис. 2). Положение этих колец (угол J) определяется средним расстоянием между молекулами или расстояниями между атомами в молекуле. Из зависимости интенсивности от угла рассеяния можно определить распределение плотности вещества.
Д. р. л. можно наблюдать также на обычной оптической дифракционной решётке при скользящем падении (меньше угла полного отражения) рентгеновских лучей на решётку. С помощью этого метода можно непосредственно и с большой точностью измерять длины волн рентгеновских лучей.
Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Боровский И. Б., Физические основы рентгеноспектральных исследований, М., 1956.
📸 Видео
2.2 Построение ЭвальдаСкачать
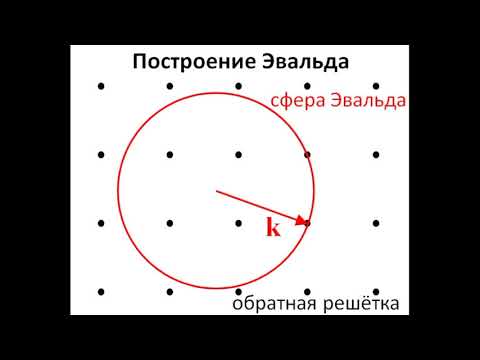
Основы нанохимии и нанотехнологий. Рентгеновская дифрактометрия. Часть 1Скачать

Дифракция света. Дифракционные решетки. 11 класс.Скачать

Введение в рентгеновскую дифракцию. Уравнение Вульфа-Бреггов.Семинар ХТТ.Скачать

Урок 420. Дифракция света. Дифракционная решеткаСкачать

Дифракция Фраунгофера. Щель и полоскаСкачать

Дифракция света ● 1Скачать

Методы рентгеноструктурного анализаСкачать
Интерпретация дифрактограмм метода рентгеновской дифрактометрииСкачать

Многофункциональный рентгеновский дифрактометр ДРОН-8Скачать

85. Дифракция Френеля и дифракция ФраунгофераСкачать

Дифракционная решеткаСкачать

Паращук Д. Ю. - Физика конденсированных сред - Рентгеновское излучение (Лекция 5)Скачать

Характеристическое рентгеновское излучениеСкачать

Двумерные дифракционные решеткиСкачать

Лабораторная работа №48. Изучение дифракции с помощью лазера и определения длины волныСкачать





