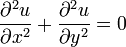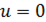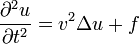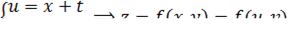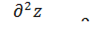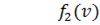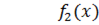Уравнение лапласа в эллипсоидальных координатах (3 видео)

Содержание

ОПЕРАТОР ЛАПЛАСА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ. ПОНЯТИЕ О ВОЛНОВОМ УРАВНЕНИИ. ПАДАЮЩАЯ И ОТРАЖЕННАЯ ВОЛНА.
Уравнение лапласа в эллипсоидальных координатах
Оператор Гамильтона. Оператор Лапласа. Понятие о криволинейных координатах
Скалярное поле
Цилиндрические координаты
🌟 Видео

Видео:Урок 5. Решение уравнения Лапласа в сферических координатахСкачать

ОПЕРАТОР ЛАПЛАСА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ. ПОНЯТИЕ О ВОЛНОВОМ УРАВНЕНИИ. ПАДАЮЩАЯ И ОТРАЖЕННАЯ ВОЛНА.

План лекции

1. Оператор Лапласа в полярной системе координат.

2. Понятие о волновом уравнении.

3. Падающая и отраженная волна.

o Оператор Лапласа в полярной системе координат

Оператор Лапласа — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом . Функции он ставит в соответствие функцию

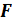
Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции: , таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом , то есть в виде скалярного произведения оператора набла на себя. Оператор Лапласа унитарен.

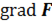
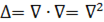
Уравнение Лапласа — дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так:

Уравнение рассматривают также в двумерном и одномерном пространстве. В двумерном пространстве уравнение Лапласа записывается:

В полярных координатах 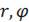уравнение Лапласа имеет вид:

o Понятие о волновом уравнении

Волновое уравнение — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики.

В многомерном случае однородное волновое уравнение записывается в виде:

где — оператор Лапласа, — неизвестная функция, — время, — пространственная переменная, — фазовая скорость.

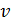
Вывод для трёхмерного случая: в одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня и записывается в виде:

Разность называется оператором Даламбера и обозначается как . Таким образом, с использованием оператора Даламбера однородное волновое уравнение записывается как:

Допустимо также рассматривать неоднородное волновое уравнение:

где 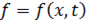— некая заданная функция внешней силы.

Стационарным вариантом волнового уравнения является уравнение Лапласа (уравнение Пуассона в неоднородном случае).

Задача нахождения нормальных колебаний системы, описываемой волновым уравнением, приводит к задаче на собственные значения для уравнения Лапласа, то есть к нахождению решений уравнения Гельмгольца, получающегося подстановкой

или .

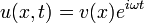
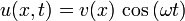
o Падающая и отраженная волна

Длинная линия — регулярная линия электропередачи, длина которой превышает длину волны колебаний, распространяющихся в ней, а расстояние между проводниками, из которых она состоит, значительно меньше этой длины волны.

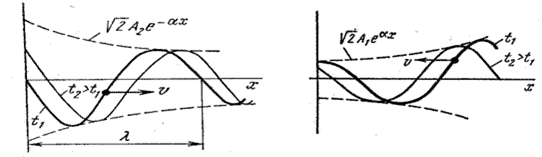
Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается подключенным к линии генератором электромагнитных колебаний, и называется падающей. Другая волна называется отражённой, и возникает из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.

*Слева – падающая волна, справа – отраженная

Физически эффект уменьшения амплитуд падающей и отраженной волн по мере их продвижения по линии объясняется наличием потерь в линии.

На рисунке слева изображены графики распределения падающей волны напряжения вдоль линии (в функции ) для двух смежных моментов времени: и . Падающая волна распространяется слева направо. При построении принято .

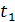
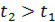
На рисунке справа представлены графики распределения отраженной волны напряжения для двух смежных моментов времени: 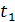и .

Отраженная волна распространяется справа налево.

Отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии называют коэффициентом отражения по напряжению и обозначают .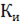

Фазовой скоростью называют скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания, или иначе: фазовая скорость — это скорость перемещения по линии неизменного фазового состояния.

Пример падающей волны:

0 1 2

Снимок волны при , при . Если , , если , то

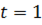
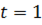
1 2

0 1 2 3

Скорость волны – .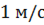

Контрольные вопросы:

1. Что такое оператор Лапласа? Уравнение Лапласа? Как записывается уравнение Лапласа в полярных координатах?

2. Что называется волновым уравнением? Как записывается волновое уравнение?

3. Что такое оператор Даламбера?

4. Что называется длинной линией, отраженной волной, падающей волной?

5. Что такое коэффициент отражения по напряжению?

Видео:6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

Уравнение лапласа в эллипсоидальных координатах

webkonspect.com — сайт, с элементами социальной сети, создан в помощь студентам в их непростой учебной жизни.

Здесь вы сможете создать свой конспект который поможет вам в учёбе.

Чем может быть полезен webkonspect.com:

простота создания и редактирования конспекта (200 вопросов в 3 клика).
просмотр конспекта без выхода в интернет.
удобный текстовый редактор позволит Вам форматировать текст, рисовать таблицы, вставлять математические формулы и фотографии.
конструирование одного конспекта совместно с другом, одногрупником.
webkonspect.com — надёжное место для хранения небольших файлов.

Видео:Оператор Лапласа в полярных координатахСкачать

Оператор Гамильтона. Оператор Лапласа. Понятие о криволинейных координатах

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

рассмотрели три основные операции векторного анализа: вычисление gradtx для скалярного поля а и rot а для векторного поля а = а(ж, у, г). Эти операции могут быть записаны в более простом виде с помощью символического оператора V («набла»): Оператор V (оператор Гамильтона) обладает как дифференциальными, так и вектор- ными свойствами.

Формальное умножение, например, умножение ^ на функцию и(х, у), будем понимать как частное дифференцирование: В рамках векторной алгебры формальные операции над оператором V будем проводить так, как если бы он был вектором. Используя этот формализм, получим следующие основные формулы: 1.

Если — скалярная дифференцируемая функция, то по правилу умножения вектора на скаляр получим где P, Q, R — дифференцируемые функции, то по формуле для нахождения скалярного произведения получим Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 3.

Вычисляя векторное произведение [V, а], получим Для постоянной функции и = с получим а для постоянного вектора с будем иметь Из распределительного свойства для скалярного и векторного произведений получаем Замечание 1. Формулы (5) и (6) можно трактовать тамке как проявление дифференциальных свойств оператора «набла» (V — линейный дифференциальный оператор). Условились считал., что оператор V действует на все величины, написанные за ним.

В этом смысле, например, — скалярный дифференциальный оператор.

Применяя оператор V к произведению каких-либо величин, надо иметь в виду обычное правило дифференцирования произведения. Пример 1. Доказать, что По формуле (2) с учетом замечания 1 получаем или Чтобы отметить тот факт, что «набл а» не действует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом с («const»), который в окончательном результате опускается. Пример 2.

Пусть u(xty,z) — скалярная дифференцируемая функция, а(х,у,г) — векторная дифференцируемая функция. Доказать, что 4 Перепишем левую часть (8) в символическом виде Учитывая дифференциальный характер оператора V, получаем . Так как ие — постоянный скаляр, то его можно вынести за знак скалярного произведения, так что а (на последнем шаге мы опустили индекс е). В выражении (V, иас) оператор V действует только на скалярную функцию и, поэтому В итоге получаем Замечай ие 2.

Используя формализм действа с оператором V как с вектором, надо помнить, что V не является обычным вектором — он не им«ет ни длины, ни направления, так что. например, вектор [V,aJ не будет, вообще говоря, перпендикулярным вектору а (впрочем, для плоского поля вектор перпендикулярен плоскости ,а значит, и вектору а).

Возможно вам будут полезны данные страницы:

Не имеет смысла и понятие коллинеарности по отношению к символическому вектору V. Например, выражение , где V и ^ — скалярные функции, формально напоминает векторное произведение двух коллинеарных векторов, которое всегда равно нулю. Однако вобшем случае это не имеет места. В самом деле, вектор = grad направлен по нормали к поверхности уровня , а вектор Vy = grad t> определяет нормаль к поверхности уровня i> = const.

Вобшем случае эти нормали не обязаны

быть коллннеарнымн (рис. 40). С другой стороны, в любом дифференцируемом скалярном поле ) имеем Эта примеры показывают, что с оператором «набла» нужно обращаться с большой осторожностью и при отсутствии уверенности в полученном результате его следует проверить аналитическими методами. §12. Дифференциальные операции второго порядка. Оператор Лапласа Дифференциальные операции второго порядка получаются в результате двукратного применения оператора V. 1.

Скалярное поле

В этом поле оператор V порождает векторное поле В векторном поле grad и можно определить две операции: что приводит к скалярному полю, и что приводит к векторному полю. 2. Пусть задано векторное поле . Тогда оператор V порождает в нем скалярное поле В скалярном поле div а оператор V порождает векторное поле 3.

В векторном поле оператор V порождает также векторное поле Применяя к этому полю снова оператор V, получим: а) скалярное поле Выберем в пространстве прямоугольнуюдекартову систему координат Oxyz и рассмотрим каждую из формул (1)-(5) более подробно. 1. Предполагая, что функция имеет непрерывные вторые частные производные , получим Символ называется оператором Лапласа, или лапласианом. Его можно представить как скалярное произведение оператора Гамильтона V на самого себя,т. е. Оператор Д (дельта) играет важную роль в математической физике.

Уравнение называется уравнением Лапласа. С его помощью описывается, например, стационарное распределение тепла. Скалярное поле и, удовлетворяющее условию , называется лапла-совым или гармоническим полем. Например, скалярное поле является гармоническим во воем трехмерном пространстве: из того, что получаем Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 2.

Пусть функция и имеет непрерывные частные производные второго порядка включительно. Тогда В самом деле, действуя формально, получим ибо как векторное произведение двух одинаковых «векторов». Tor же результат можно получить, используя выражения градиента и ротора в декартовых координатах Пусть задано векторное поле координаты которого P, Q, R имеют непрерывные частные производные второго порядка. Тогда получим 4. При тех же условиях, что и в пункте 3, имеем Это соотношение уже было доказано ранее путем непосредственных вычислений.

Здесь мы приведем его формальное доказательство, используя известную формулу из векторной алгебры Имеем как векторное произведение двух одинаковых «векторов». 5. Покажем, наконец, что при тех же условиях, что и ранее, Так как то, полагая в формуле для двойного векторного произведения получим Поэтому окончательно будем иметь где grad diva выражается по формуле (8), а Да для вектора надо понимать так:. В заключение приведем таблицу дифференциальных операций второго порядка. Скалярное поле Векторное поле Заштрихованные прямоугольники означают, что соответствующая операция не имеет смысла (например, градиент от. § 13.

Понятие о криволинейных координатах Во многих задачах бывает удобно определять положение точки пространства не декартовыми координатами ), а тремя другими числами (qh 42,4з), более естественно связанными с рассматриваемой части ой задачей. Если задано правило, согласно которому каждой точке М пространства отвечает определенная тройка чисел и, обратно, каждой такой тройке чисел отвечает единственная точка М, то говорят, что в пространстве задана криволинейная координатная система.

В этом случае величины ф, называют криволинейными координатами точки М. Координатными поверхностями в системе криволинейных координат qtqi, Яз называются поверхности На координатных поверхностях одна из координат сохраняет постоянное значение. Линии пересечения двух координатных поверхностей называются координатными линиями. В качестве примеров криволинейных координат рассмотрим цилиндрические и сферические координаты. 13.1.

Цилиндрические координаты

В цилиндрических координатах положение точки М в пространстве определяется тремя координатами: (р = const — полуплоскости, примыкающие к оси Oz z = const — плоскости, перпендикулярные оси Oz (рис. 41). Координатные линии: 1) линии (р) — лучи, перпендикулярные оси Oz и имеющие начало на этой оси, т.е. линии пересечения координатных поверхностей у? = const, z = const; 2) линии (ip) — окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных оси Oz 3) линии (z) — прямые, параллельные оси Связь декартовых координат точки с цилиндрическими координатами ( задается формулами 13.2.

Сферические координаты В сферических координатах положение точки Af в пространстве определяется следующими координатами: Координатные поверхности (рис.42): г = const — сферы с центром в точке О; • в = const — круговые полуконусы с осью полуплоскости, примыкающие к оси Oz. Координатные линии: 1) линии (г) — лучи, выходящие източки О; 2) линии (в) — меридианы на сфере; 3) линии — параллели на сфере. Связь декартовых координат (х, у, z) точки М с ее сферическими координатами задается формулами.

Введем единичные векторы (орты), направленные по касательным к коор-динатнымлиниям вточке М всторонувозрастанияпеременных qx, q2, соответствен но. Определение. Система криволинейных координат называется ортогональной, если в каждой точке М орты попарно ортогональны. В такой системе ортогональны и координатные линии, и координатные поверхности. Примерами ортогональных криволинейных координат служатсистемы цилиндрических и сферических координат.

Мы ограничимся рассмотрением только ортогональных систем координат. Пусть — радиус-вектор точки М — Тогда можно показать, что Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты Аналогично для сферических координат имеем Величины являются дифференциалами длин дуг соответс твующих координатных линий.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.