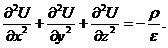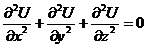Уравнение лапласа и пуассона для электростатического потенциала (4 видео)

Уравнения Пуассона и Лапласа

Уравнения Пуассона и Лапласа являются основными дифференциальными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме. Действительно, подставляя в уравнение

вместо величин Е_х; Е_у; Е_z их выражения через потенциал:

Это дифференциальное уравнение носит название уравнения Пуассона.

является решением уравнения Пуассона для случая, когда заряды распределены в конечной области пространства.

Если в рассматриваемой области пространства отсутствуют объемные электрические заряды, то уравнение Пуассона получает вид

и называется в этом частном случае уравнением Лапласа.

Отметим, что в цилиндрической и сферической системах координат уравнение Пуассона и Лапласа имеют другую форму записи. Поэтому данные уравнения часто записывают в виде, не зависящем от системы координат:

Оператор ? 2 часто обозначают и называют оператором Лапласа или лапласианом.

При интегрировании уравнения Лапласа (или Пуассона) в решение входят постоянные интегрирования. Их определяют из граничных условий.

Содержание

Уравнение Пуассона и Лапласа
Пример 1
Решение
Пример 2
Решение
Уравнение Пуассона и уравнение Лапласа
Уравнение Пуассона и уравнение Лапласа
📺 Видео

Видео:Формула ПуассонаСкачать

Уравнение Пуассона и Лапласа

В случае потенциального поля напряженность поля Е может быть выражена через градиент потенциала. При этом приходим к выражению

содержащему двойную дифференциальную операцию: дивергенцию от градиента. При использовании декартовой системы координат легко записать эту операцию через соответствующие производные. Действительно, представляя в формулу (1) составляющие grad φ как:

Операция div grad носит название лапласиана и обозначается знаком Δ. Используя оператор набла, рассматриваемую операцию можно представить как наблу квадрат, таким образом:

В случае декартовых координат и в применении к скалярной функции можно всегда считать операции ∇ 2 и Δ тождественными.

Уравнение (1) является основным уравнением потенциального электрического поля и носит название уравнения Пуассона.

В области поля, где заряды отсутствуют (где ρ = 0), уравнение (1) упрощается, так как в его правой части оказывается нуль. В последнем случае уравнение называют уравнением Лапласа.

и было названо дифференциальным уравнением электрического потенциального поля.

Рассмотрим несколько примеров.

Пример 1

В некоторой области поля потенциал изменяется по закону:

Содержится ли в этой области объемный заряд и чему он равен?

Решение

Путем прямого дифференцирования найдем:

Уравнение Лапласа удовлетворяется (объемный заряд равен нулю).

Пример 2

То же, что и в предыдущем примере, но описанное следующим уравнением:

Решение

Очевидно, что правая часть данного равенства в общем случае не равна нулю.

Примечание к примерам 1 и 2. Из рассмотрения встретившихся видов произведений можно сделать более общий вывод:

всегда удовлетворяет уравнению Лапласа (первый множитель в формуле (5) cos или sin, а второй ch или sh).

Видео:ЧК_МИФ 3_1_2_4 (L=3- ЛЭТИ) УРАВНЕНИЕ ПУАССОНА ДЛЯ СКАЛЯРНОГО ПОТЕНЦИАЛАСкачать

Уравнение Пуассона и уравнение Лапласа

Видео:Билет №04 "Потенциал электростатического поля"Скачать

Уравнение Пуассона и уравнение Лапласа

Уравнение Пуассона и уравнение Лапласа. Уравнение Пуассона и уравнение Лапласа являются основными уравнениями статического электричества. Они следуют теореме Гаусса в дифференциальной форме.

Действительно, E = -grad cf. В то же время, согласно теореме Гаусса, div £ = (13.21) e. Подставим E из (13.6) в (13.21). div E = div (-grad ” dv2′ de (13.29) y2 ^

не выводится в цилиндрической системе (13.30) Людмила Фирмаль

сферическая система координат V2 ± Д / ^ 2 ^ _ _ |! A / Sino ^ 1? Ф. (13.31) R2 dR dR) 1 /? 2sinOдЭ дБ) 1 sin2 0 yes2 ‘ * * Уравнение Пуассона зависит от второй производной от φ в любой точке электрического поля и объемной плотности свободного заряда в этой точке электрического поля.

В то же время потенциал φ в любой точке электрического поля, конечно, зависит не только от величины свободного заряда, но и от всех зарядов, создающих электрическое поле, уравнение Лапласа (1780) описывает потенциальное поле небесной механики

Сначала был применен, а затем используется для описания электрического поля. Уравнение Пуассона применяется для изучения электрических потенциальных полей (электрических и магнитных полей) с 1820 года.

Подумайте о том, как вообще можно записать решение уравнения Пуассона. Объем V имеет объем (р), поверхность (о) и линейные (т) заряды. Эти заряды выражаются в виде набора точечных зарядов pdV, ®ds, rd /. dV — элемент объема, ds — элемент заряженной поверхности, а

dl — элемент длины заряженной оси. Людмила Фирмаль

Согласно уравнению (13.19), составляющая потенциала dq в точке пространства p от pdV равна p dV — 4 l? Потенциальные компоненты поверхностного заряда R и линейного заряда определяются аналогично, рассматривая их как точечные заряды: o ds td / 4 rciR 4neR полное значение (p — сумма потенциальных компонентов всех зарядов в поле (интеграл )

Определяется как: f pdV | 1 f ods .1 C Td / JR4шJR 4ne JR 1