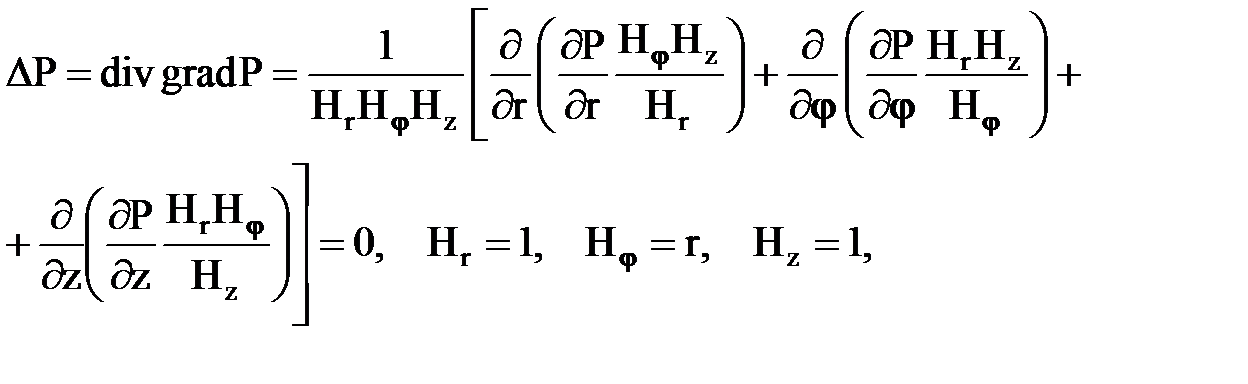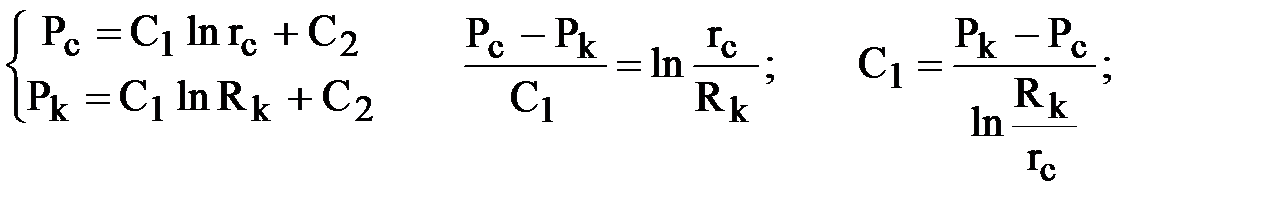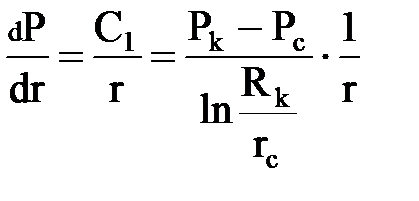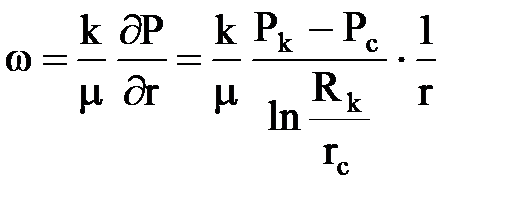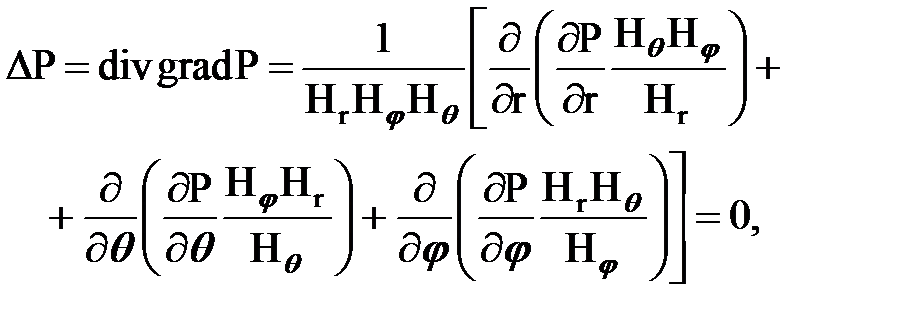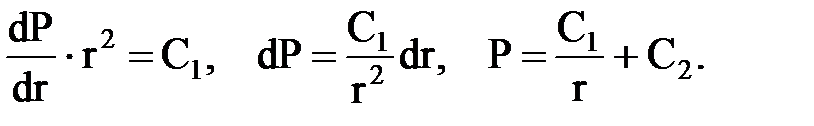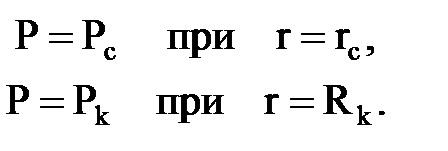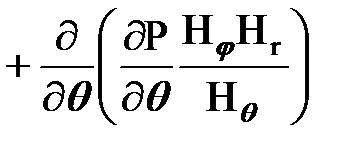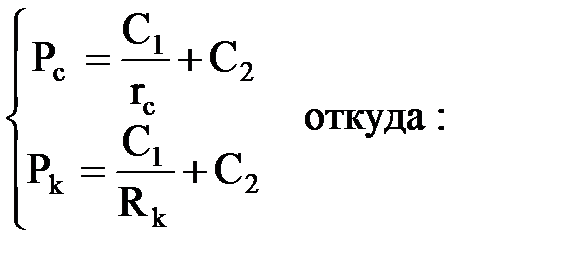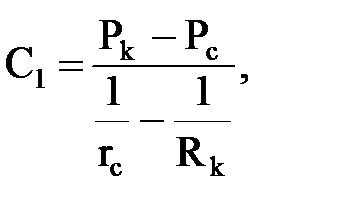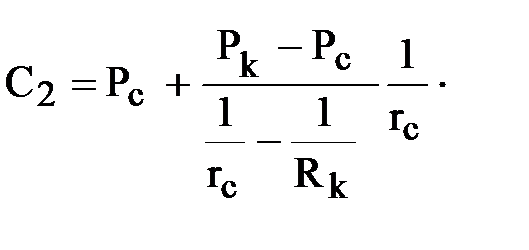Одномерным называется фильтрационный поток жидкости, в котором скорость фильтрации и напор являются функциями только одной координаты, отсчитываемой вдоль линии тока.
К одномерным относятся следующие потоки.
1. Прямолинейно-параллельный фильтрационный поток.
Контур питания для одной скважины – это условный контур, окружающий скважину, за пределами которого можно пренебречь возмущающим влиянием добывающей скважины. Для одиночной скважины – таким контуром является окружность такого радиуса, при котором на ней Р = Рпл = Pk и w = 0. Для прямолинейной батареи скважины контур питания (условия на котором Р = Рk и w = 0 сохраняются) также становится прямолинейным.
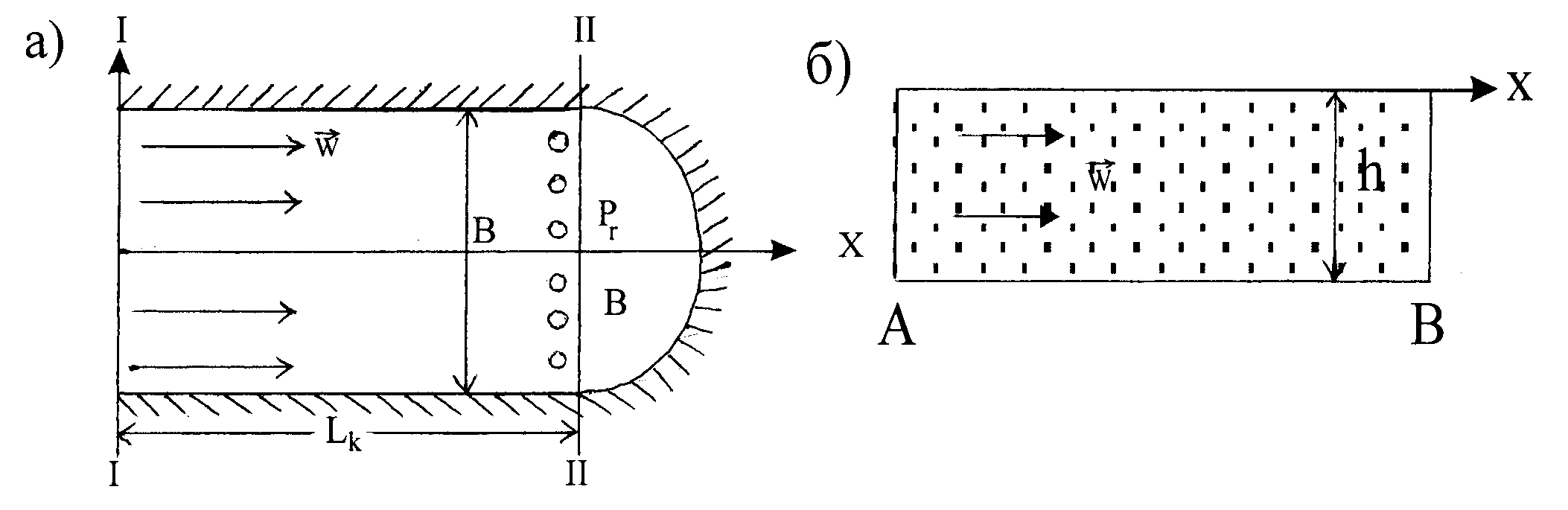
Для прямолинейно-параллельного фильтрационного потока линии тока жидкости в плане пласта и в его продольном сечении являются прямыми линиями, а скорость v в любой точке вертикального сечения пласта одинакова. Такой фильтрационный поток возникает при эксплуатации однородного пласта прямоугольной формы, у которого на контуре питания поддерживается постоянным давление Рк, а батарея скважин, у которых давление на забое Рr, расположена параллельно контуру питания (рис.10.1).
 |
 |
Рис. 10.1 План модели (а) и разрез по линии OX (б)
Условныеия обозначения: — линии тока жидкости; — батарея (галерея) добывающих скважин; I-I – контур питания; II-II – линия размещения батареи скважин; В – ширина разрабатываемого месторождения (зоны); Lk – расстояние от контура питания до батареи скважин; h – мощность пласта; v- вектор скорости фильтрации
2. ) Плоскорадиальный параллельный фильтрационный поток.
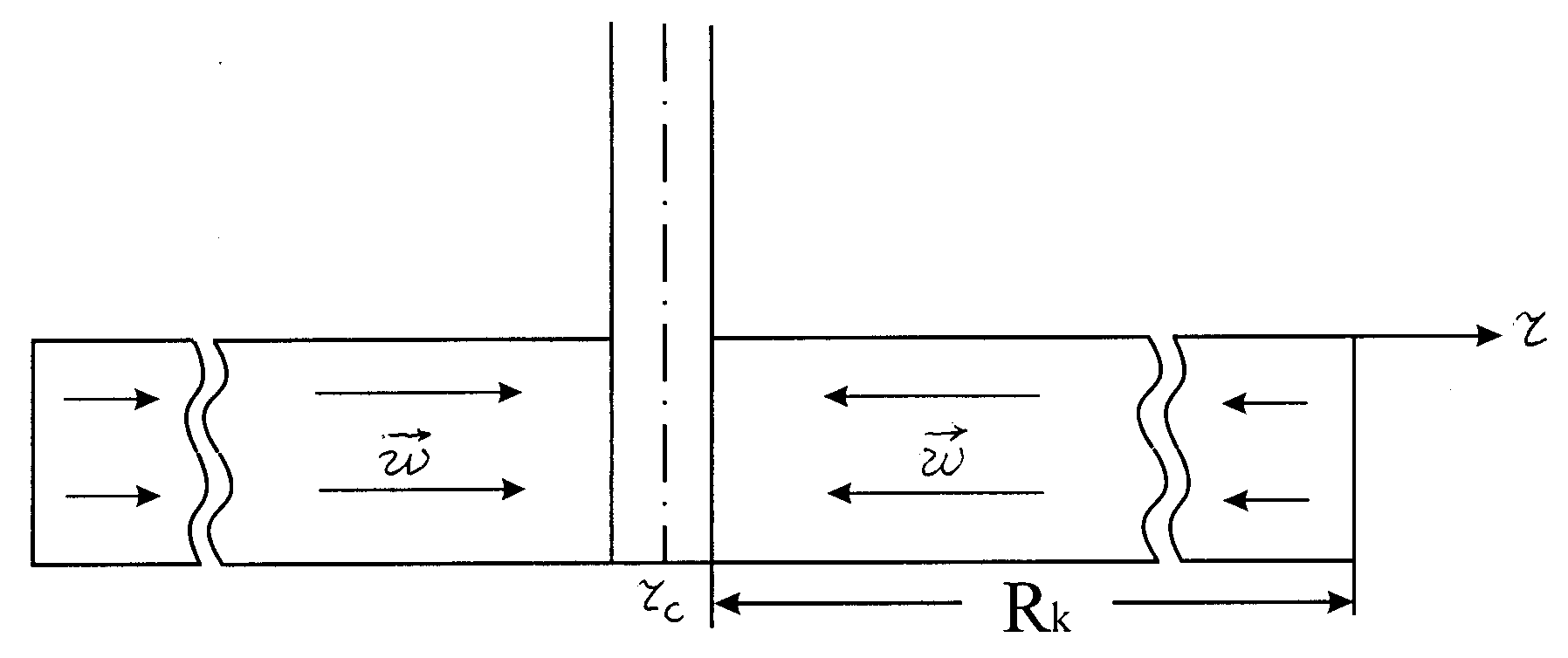
Особенность плоскорадиального потока заключается в том, что линии тока совпадают с радиусами, сходящимися к центру окружности (скважине) и находятся в одной плоскости. В любом горизонтальном сечении пласта поведение линий тока одинаково. Плоскорадиальный поток создается в однородном круговом пласте постоянной мощности или пласте
неограниченной протяжности, если в центре него пробурена скважина, вскрывшая пласт на всю мощность и имеющая открытый ствол (рис. 10.2 и 10.3).
| Рис. 10.3 Линии тока жидкости в вертикальном сечении пласта. |
| w |
| скважина |
| rk, Pc |
| Rk, Pk |
| r |
| Рис. 10.2 Линии тока жидкости в пласте. |
1) Радиально-сферический фильт
3. Радиально-сферический фильтрационный поток.
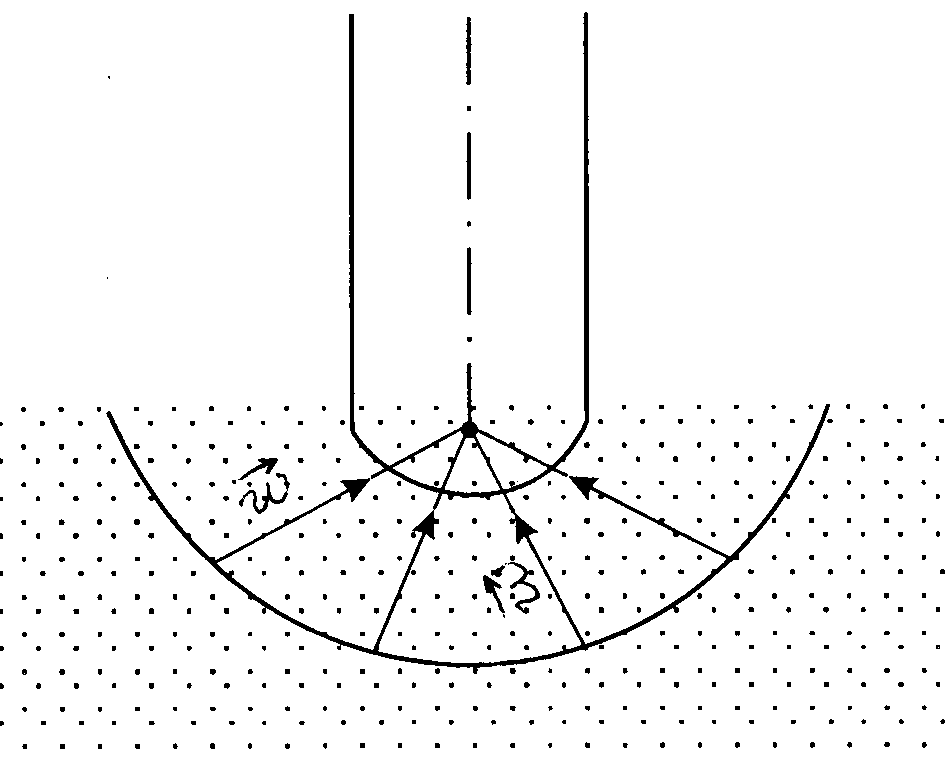
Линии тока этого потока сходятся к центру сферы. Такой поток будет в пласте неограниченной мощности, вскрытом скважиной, имеющей полусферический забой (рис. 10.4).
Описанные три вида фильтрационных потоков являются простейшими моделями реальных течений, возникающих при разработке месторождений и играющих важную роль для практических расчетов.
Задача исследования заключается в определении гидродинамических характеристик: дебита (или расхода), давления, grad P и скорости фильтрации в каждой точке пласта, а также в установлении закона движения частиц вдоль их траекторий, и определения средневзвешенного по объему порового пространства пластового давления.
3.5.1. Прямолинейно-параллельный фильтрационный поток.
Пусть в горизонтальном пласте толщины h и ширины В в сечении I-I, совпадающем с контуром питания, поддерживается постоянное давление Рк, а в сечении II-II, отстоящем на Lк, поддерживается давление Рr в батарее добывающих скважин (рис. 10.1).
Дифференциальное уравнение Лапласа для такого течения: 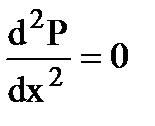
Интегрируя дважды, имеем:
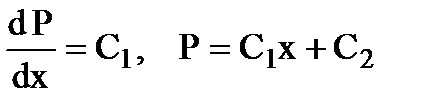
Постоянные интегрирования определим из граничных условий (начальных условий нет, т.к. движение установившееся, т.е. не зависит от t).
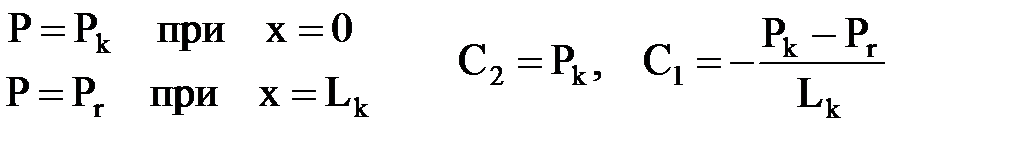
Решением уравнения Лапласа будет функция Р(х) (распределение давления):
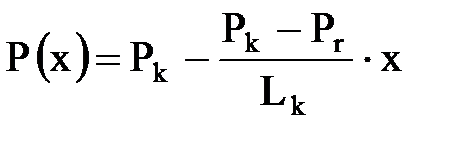
Находим из уравнения движения скорость фильтрации в пласте
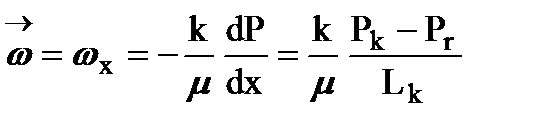
Находим объемный расход жидкости в потоке как произведение скорости фильтрации w на площадь поперечного сечения пласта S = Bh, т.е.
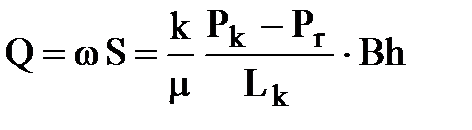
Находим закон движения t = f (x), используя связь между скоростью фильтрации и скоростью движения частиц жидкости
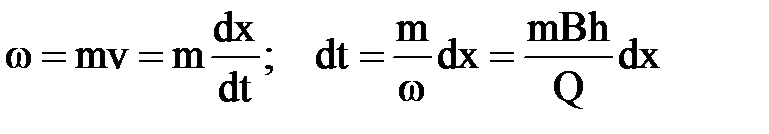
Интегрируя по t от 0 до t и по х от 0 до х, получим
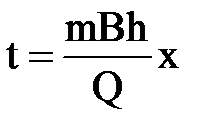
Видео:Уравнение Лапласа (ФКП)Скачать

Вычисляем средневзвешенное по объему порового пространства пластовое давление
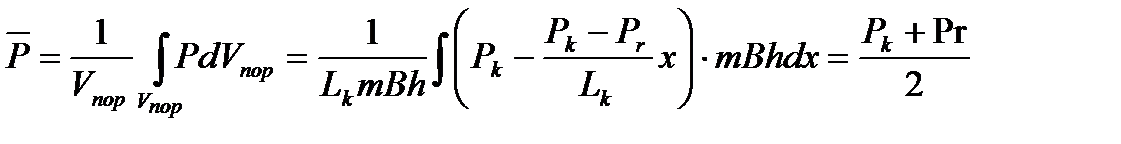
Поведение найденных характеристик плоскопараллельного фильтрационного процесса показано на рис. 10.5 и рис.10.6.
| P |
| Q-const |
| w-const |
| х |
| Рис. 10.5 Изменение характеристик вдоль линий тока. |
| Рис. 10.6 Гидродинамическое поле плоскопараллельного фильтрационного процесса. |
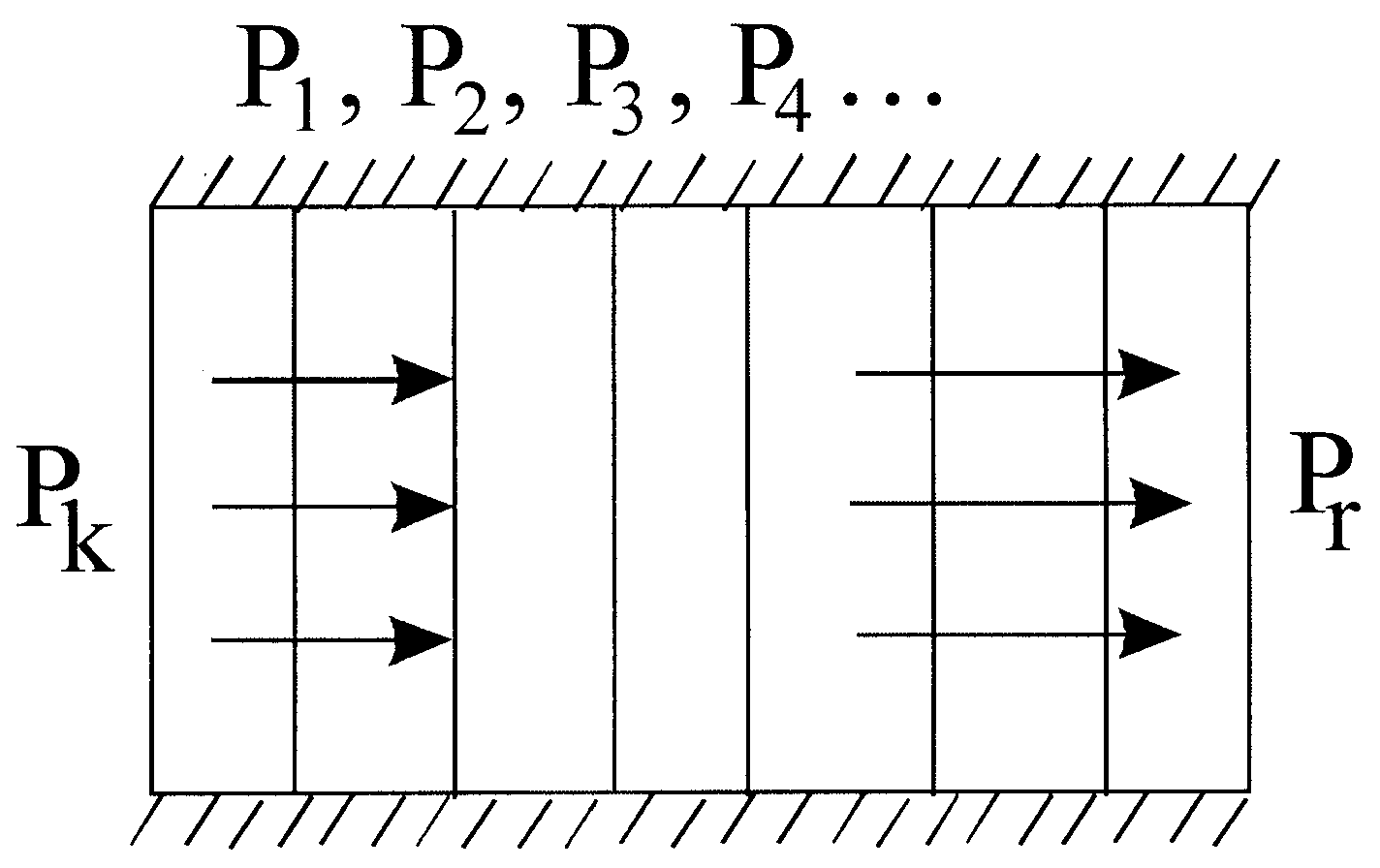
При фильтрации давление равномерно падает от Pk до Pr. Линии равного давления (изобары) на плоскости перпендикулярны кровле и почве пласта и равноотстоят друг от друга. Линии тока жидкости являются параллельными прямыми и перпендикулярны к изобарам. Поведение изобар и линий тока жидкости в пласте определяет гидродинамическое поле данного фильтрационного потока (рис. 10.6).
Лекция № 11
3.5.2 Плоскорадиальный фильтрационный поток.
Лекция № 11
Будем считать, что несжимаемая жидкость притекает к гидродинамической совершенной скважине радиусом rc, расположенной в центре однородного горизонтального кругового пласта, толщиной h. На внешней круговой границе пласта радиусом Rk, служащей контуром питания, поддерживается постоянное давление Pk, на забое скважины давление Рс тоже постоянно. Дифференциальное уравнение Лапласа в случае плоскорадиального фильтрационного потока имеет вид
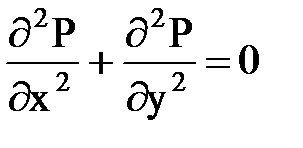
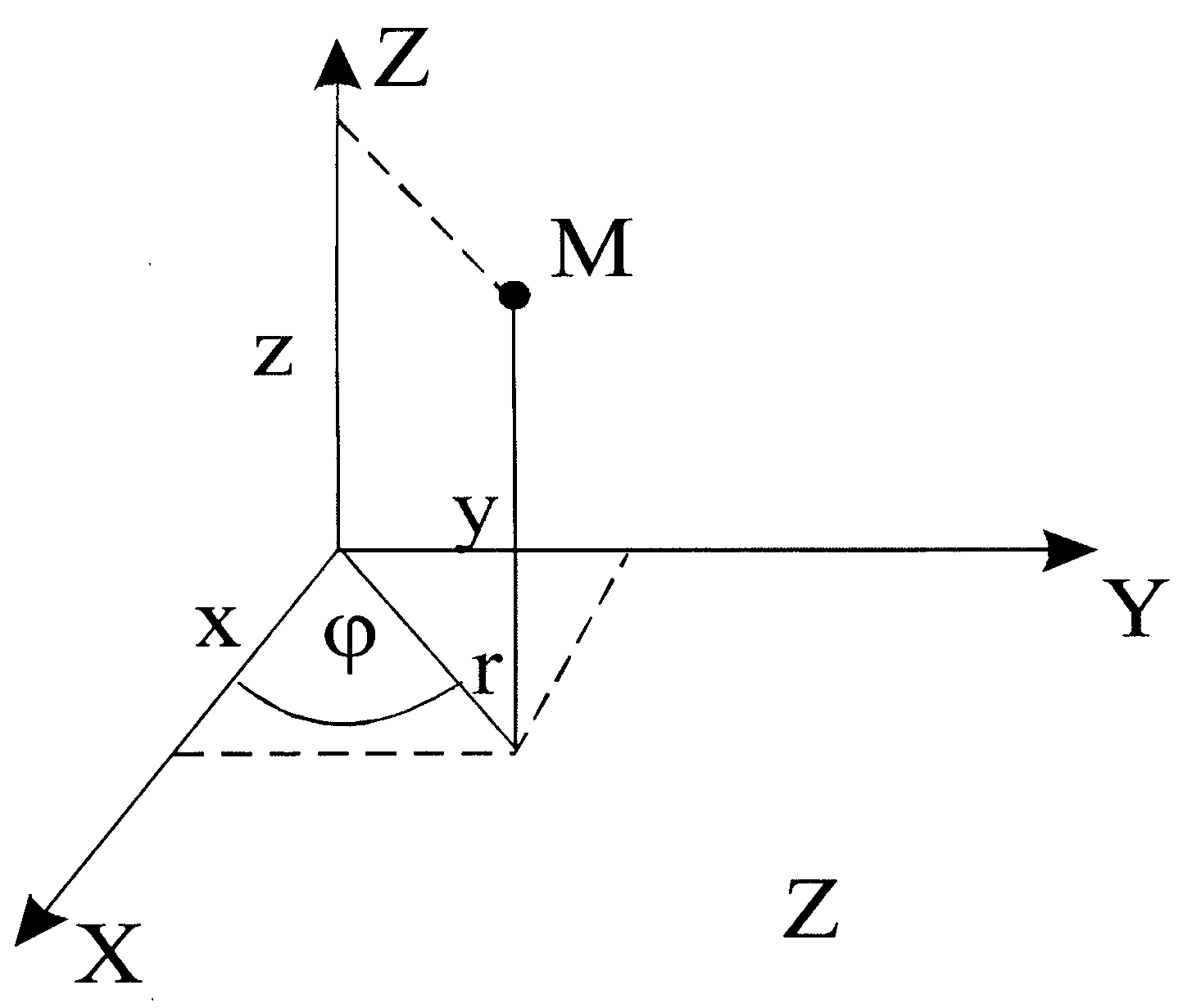
Удобно перейти и решить задачу в цилиндрической системе координат (r,j,z) (рис. 11.1).
| Рис. 11.1 Связь координат декартовой и цилиндрической систем: x = r cos j y = r sin j z = z |
| Рис. 11.2. |
Уравнение Лапласа в криволинейной системе ( цилиндрической) системе координат:
Линии тока жидкости для данной фильтрационной модели совпадают с радиусами окружности (рис. 11.2). Поэтому в уравнении Лапласа останется одно слагаемое, зависимое от координаты r, и после подстановки в него значений коэффициентов Ляме примет вид:
Получаем
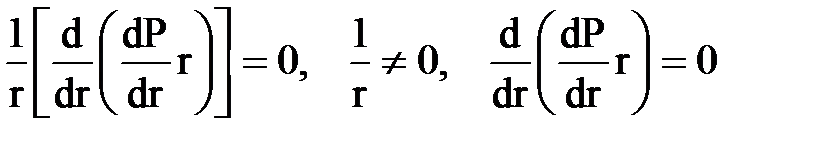
Это и есть дифференциальное уравнение Лапласа в цилиндрических полярных координатах для установившегося плоскорадиального течения несжимаемой жидкости по закону Дарси.
Дважды проинтегрировав дифференциальное уравнение, получаем
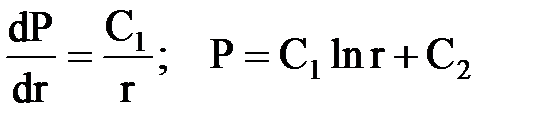
Постоянные интегрирования С1, С2 находим как обычно из граничных условий Р = Рc при r = rc; Р = Рк при r = Rk.
Подставляя граничные условия, получаем систему уравнений для нахождения С1, С2:
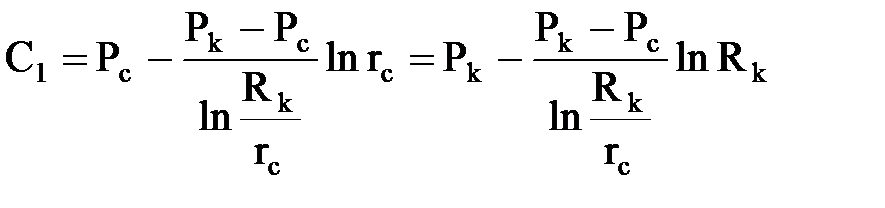
Подставляя найденные значения С1 и С2 в решение, получим зависимость давления от координаты r в плоскорадиальном потоке.
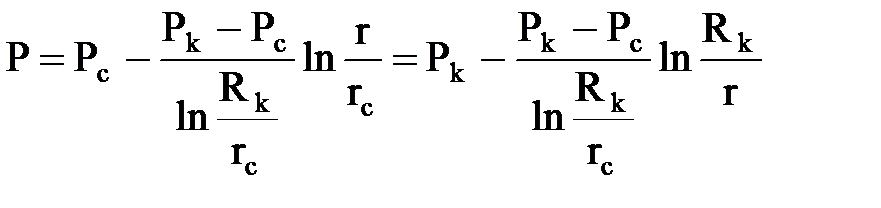
Находим градиент давления
и используем его для нахождения скорости фильтрации
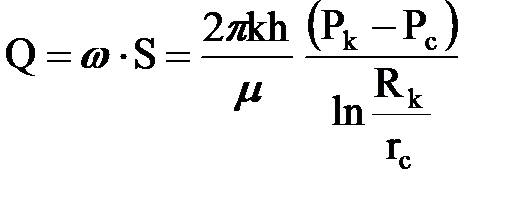
где: S = 2prh – поверхность фильтрации (боковая поверхность цилиндра радиуса r и высотой h) (рис. 11.3).
Формула 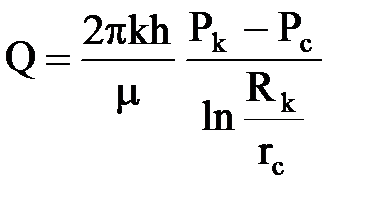
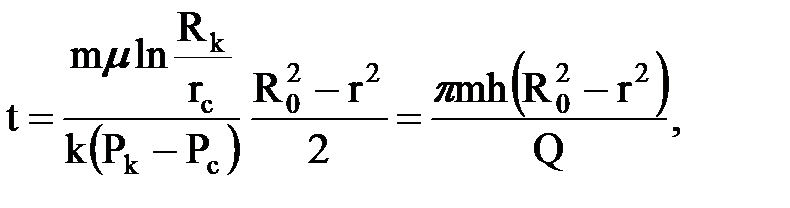 |
Находим закон движения частиц из связи 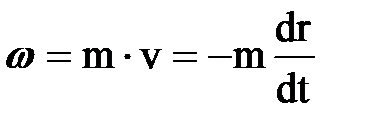 ; ; 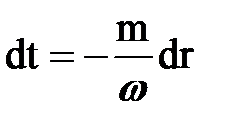 . Подставляя сюда значение w и интегрируя от 0 до t и от R0 до переменного r получим: . Подставляя сюда значение w и интегрируя от 0 до t и от R0 до переменного r получим: |
| Рис. 11.3. |
где: R0 – начальное положение частицы в момент t = 0 и r – текущее положение в момент t.
Если в эту формулу подставить вместо R0 ®Rк , а вместо r ® rc, то получим время Т отбора всей жидкости, находящейся в пласте
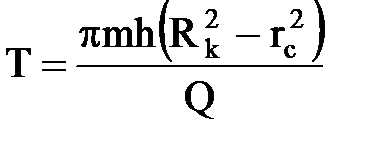
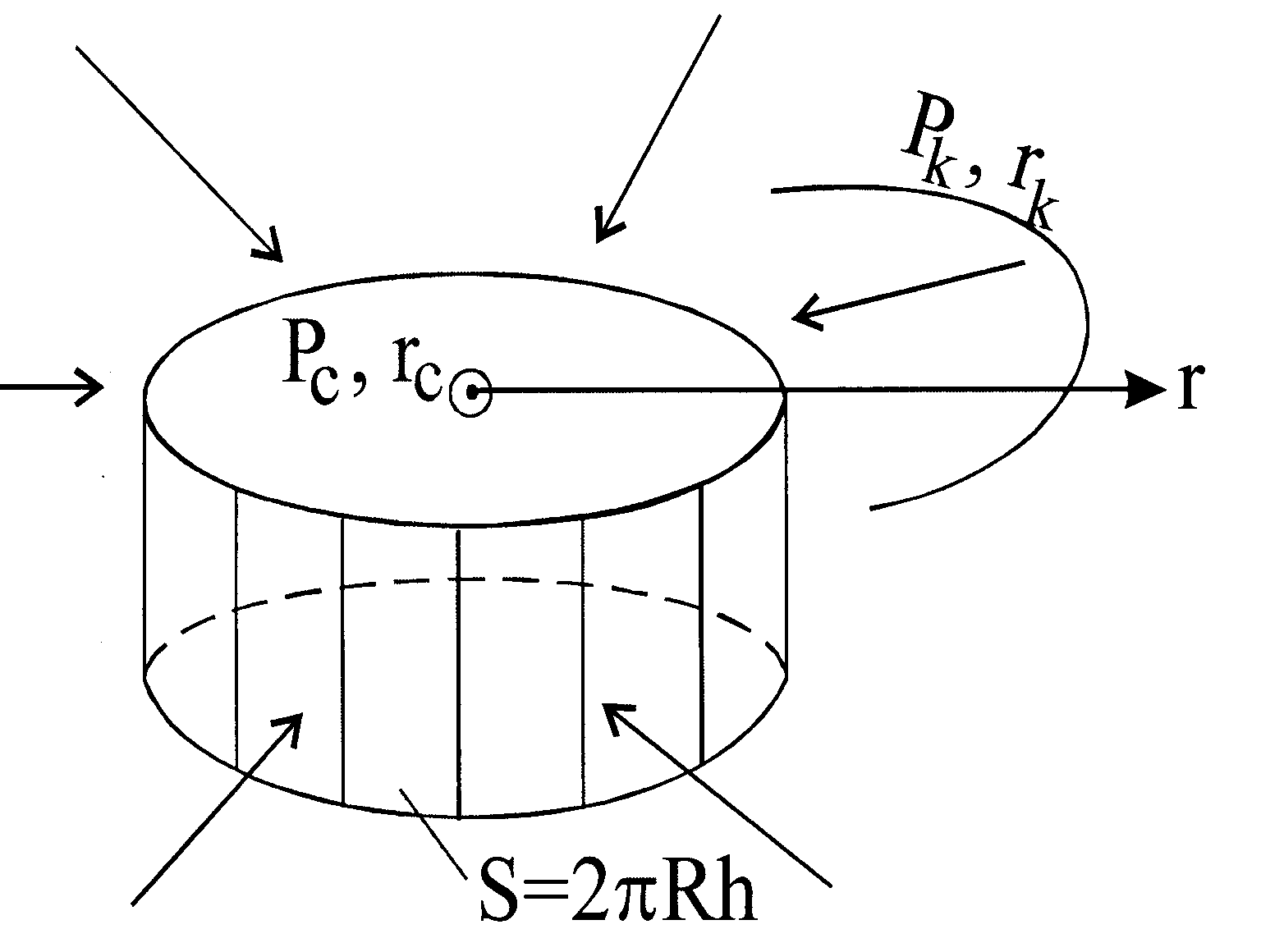
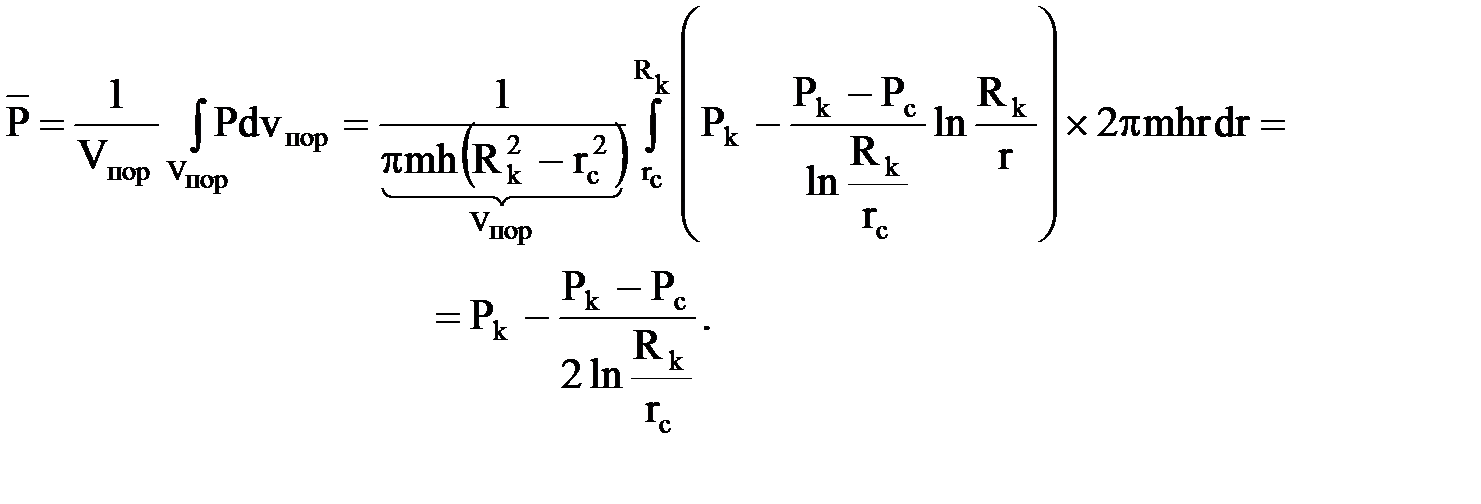
Находим средневзвешенное по объему порового пространства пластовое давление
Прокомментируем некоторые результаты.
Дебит скважины пропорционален депрессии DР (разнице давлений в пласте и на забое работающей скважины) и одинаков через любую цилиндрическую поверхность, соосную со скважиной т.е. не зависит от r.
Отношение объемного дебита скважины к DР называется коэффициентом продуктивности
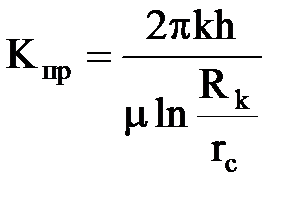
.Через этот коэффициент дебит скважины выражается уравнением
Q=KпрDP , которое называется индикаторной диаграммой. На ней коэффициент продуктивности определяется как тангенс угла наклона прямой к оси DP (tg j = Kпр). На практике индикаторную диаграмму строят по данным испытания скважины, путем получения притоков нефти при различных депрессиях.
| rc |
| r |
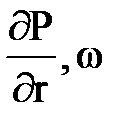 |
| Q |
| DP |
| j |
| Рис. 11.4 |
| Рис. 11.5 График зависимости скорости и градиента давления от расстояния до скважины. |
Градиент давления и скорости фильтрации ведут себя одинаково и резко возрастают при приближении к скважине (рис. 11.5).
Логарифмическая кривая давления, вращение которой вокруг скважины образует поверхность, называется воронкой депрессии. Основная часть депрессии образуется в призабойной зоне, параметры которой сильно влияют на дебит скважины (рис. 11.6).
 |
| Rk Rk |
| Рс |
| rc |
| а) |
| скважина нагнетательная |
| скважина добывающая |
| б) |
 |
| rc |
| Рис. 11.6 Воронка дисперсии (а) и гидродинамическое поле (б) |
Гидродинамическое поле плоскорадиального потока описывается семействами изобар и линий тока. Изобара представляет окружности, поскольку, Р
Видео:Билет №04 "Потенциал электростатического поля"Скачать

3.5.3 Радиально-сферический фильтрационный поток
Лекция № 12
 |
 |
 |
 |
| r |
| rc |
| Рис. 12.1 Линии тока в радиально-сферическом потоке |
Будем считать, что несжимаемая жидкость притекает к скважине, вскрывающей бесконечный по мощности однородный пласт, через сферический забой радиуса rc. Схема такого потока изображена на рисунке 12.1.
| Дифференциальное уравнение Лапласа удобно решать в сферической системе координат (r, q, j)., т.к. линии тока жидкости совпадают с радиусами полусферы и зависят от одной координаты r. |
 |
где: Нr, Нq, Нj — коэффициенты Ламэ в (r, q, j) : x = r sinq´cosj; y = r sinq ´sinj; z= r cosq (рис. 12.2).
| Рис. 12.2 |
Hr = 1; Hq = r; Hj = r sinq.
Для рассматриваемой модели линии тока жидкости совпадают с радиусами полусферы, поэтому В уравнении Лапласа частные производные по координатам q и j равны 0 и уравнение Лапласа будет иметь вид:
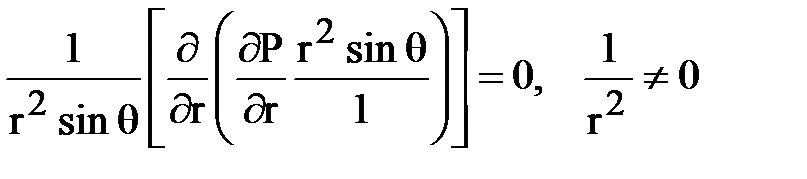
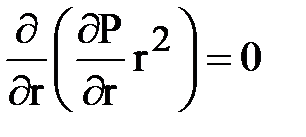
Далее схема решения и нахождения характеристик потока жидкости полностью аналогична плоскорадиальному потоку. Дважды интегрируя, получим
Постоянные С1 и С2 определяем из граничных условий:
Подставив граничные условия, находим С1 и С2 из системы уравнений:
После подстановки значений С1 и С2 в общее решение, получим распределение давления в потоке несжимаемой жидкости как функции от координаты r
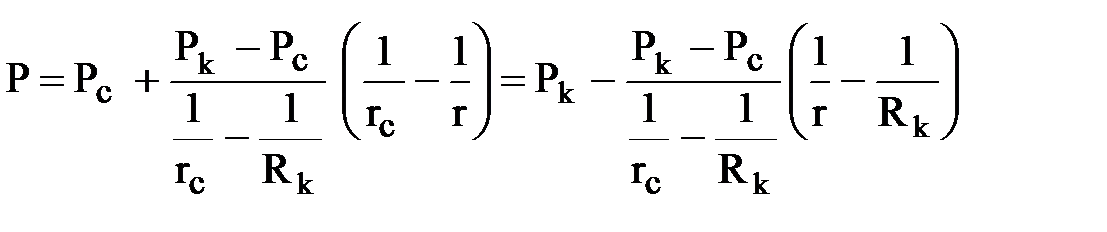
Если сопоставить формулы распределения давления для плоскорадиального и радиально-сферического потоков, то нетрудно заметить, что они имеют одинаковую структуру и переходят друг в друга, если логарифм отношения расстояний заменить разностью обратных значений расстояний:
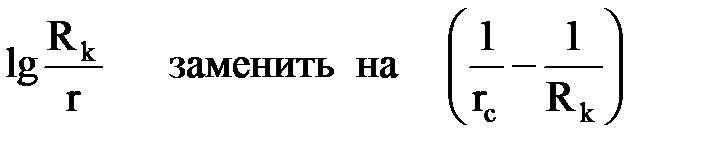
Такое подобие структур формул характерно для выражений всех гидродинамических характеристик. Поэтому все остальные характеристики радиально-сферического потока (объемный расход несжимаемой жидкости, распределение скорости фильтрации, средневзвешенное давление и др.) можно получить из характеристик плоскорадиальной фильтрации аналогичной заменой в соответствующих формулах.
1.15. Расчет одномерных электростатических полей по уравнениям Пуассона и Лапласа
Электростатическое поле в однородной среде с постоянной диэлектрической проницаемостью полностью характеризуется уравнением Пуассона (1.11) или (если в рассматриваемой области отсутствуют объемные связанные заряды) уравнением Лапласа (1.12).
Наиболее просто уравнения Пуассона и Лапласа решаются в случае одномерных полей, потенциалы которых зависят только от одной координаты. При этом дифференциальные уравнения в частных производных переходят в обыкновенные дифференциальные уравнения второго порядка, решение которых при известных граничных условиях является несложной задачей.
Так, в прямоугольной системе координат уравнения Пуассона и Лапласа для одномерного поля будут иметь следующий вид:

Решение уравнения (1.22), очевидно, может быть получено лишь тогда, когда объемная плотность заряда r и абсолютное значение диэлектрической проницаемости e заданы как функции координат во всем пространстве. Например, если объемная плотность r изменяется вдоль оси ОХ по закону
(где коэффициент а и показатель степени n являются постоянными), то, в случае, когда e=const, частное решение уравнения Пуассона будет иметь следующий вид:
где С1 и С2 – постоянныеинтегрирования, которые определяются из граничных условий.
В случае, когда объемная плотность заряда r также является постоянной величиной, решение имеет вид
Частное решение уравнения Лапласа (1.29) можно представить следующим образом:
В цилиндрической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят от того, функцией какой координаты является искомый потенциал U. Например, если потенциал U зависит только от радиальной координаты r (U=U(r)), то уравнения (1.11) и (1.12) будут иметь вид


Решение уравнения (1.26) определяется видом функции r. Если, например, объемная плотность заряда r изменяется вдоль радиуса r по закону
то искомое решение будет иметь вид:
Для случая, когда объемная плотность заряда r не зависит от координаты r, решение уравнения (1.26) можно представить следующим образом:
Решение уравнения Лапласа (1.27) имеет вид:
Если искомый потенциал является функцией только одной угловой координаты j, то уравнения Пуассона и Лапласа приобретают следующий вид:

Видео:Урок 202. Давление под искривленной поверхностью жидкости. Формула ЛапласаСкачать

При постоянном значении r уравнение (1.31) имеет частное решение

Решение уравнение Лапласа (1.32) можно записать следующим образом:
В сферической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят также от того, функцией какой координаты является искомый потенциал U.
Так, если потенциал U зависит только от радиальной координаты r, то уравнения Пуассона и Лапласа будут иметь вид:
При изменении объемной плотности заряда r по закону

решение уравнения (1.35) можно представить следующим образом:
Если r является постоянной величиной, решение будет иметь вид
Уравнение Лапласа (1.36) имеет следующее решение:
В случае, если потенциал U зависит только от одной координаты q, уравнение Лапласа (1.12) будет иметь вид
Решение этого уравнения можно представить следующим образом:
Если потенциал U является функцией только одной координаты j, то уравнение (1.12) будет иметь вид
а его решение является линейной функцией этой координаты
Пример 1. Плоский конденсатор с двумя слоями диэлектрика подключен к источнику постоянного напряжения U0=100В (рис. 1.25). Относительные значения диэлектрической проницаемости слоев er1=3, er2=6. Толщина слоев – d1=d2=1мм.
Один из слоев заряжен с объемной плотностью r, которая изменяется по толщине по закону r=10 -4 х Кл/м 3 .
Пренебрегая краевым эффектом, найти распределение потенциала и напряженности поля в слоях диэлектрика.
Построить графики изменения потенциала и напряженности электрического поля вдоль оси ОХ.
Данная задача по расчету электрического поля является одномерной. В первом слое электрический потенциал отвечает уравнению Лапласа (1.23), а во втором – уравнению Пуассона (1.22). Решение этих уравнений можно представить с помощью выражений (1.24) и (1.25) , соответственно, при n=1 и а=1.
Для определения постоянных интегрирования используем граничные условия на внешних границах области и на границе раздела двух диэлектриков (внутренней границе).
Будем при этом считать, что правая пластина имеет нулевой потенциал.

Здесь D1 и D2 – нормальные составляющие вектора электрического смещения.
Из первого равенства следует, что С2=U0.
Перепишем три следующих граничных условия, подставляя в них соответствующие выражения для потенциалов и вектора электрического смещения:
Решая последнюю систему из трех уравнений относительно неизвестных С1, С3, и С4, получим С1=-66670,
Таким образом, окончательно выражения для напряженности поля и потенциалов можно записать в виде:
Графики изменения потенциала и напряженности поля представлены на рис. 1.26 
На графике все значения представлены в относительных единицах, причем за базисные значения приняты значения потенциала и напряженности поля на поверхности левой пластины (Ub=100 В, Eb=66670 В/м).

Найти законы изменения потенциала и напряженности поля в функции расстояния от оси цилиндра. Построить графики изменения указанных функций вдоль радиуса.
Решение. Поле в данном случае является одномерным, поскольку напряженность поля и потенциал зависят только от одной радиальной координаты.
Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

При решении задачи по расчету электрического поля в заданной области, эту область необходимо разбить на три подобласти. В первой из них (0?r?R1) поле отсутствует (Е=0). Во второй подобласти (R1?r?R2) электрический потенциал отвечает уравнению Пуассона (1.26), а в третьей (R2? r??) – уравнению Лапласа (1.27), которые имеют решения (1.28) (при n=1,a=0.1) и (1.30).
Перепишем эти решения в следующем виде:
Здесь индексы у потенциалов обозначают их принадлежность ко второй и третьей подобластям.
Постоянные интегрирования определим из граничных условий, которые можно поставить как из классических граничных условий, так и из следующих соображений. Поскольку поле внутри цилиндра отсутствует, то при r=R1, можно принять Е2=0.
Отсюда сразу определяем постоянную С1=7.533. Примем потенциал равным нулю на наружной поверхности цилиндра (U2=0 при r=R2), тогда
и, таким образом, С2=106.335.
Потенциал U3 со стороны третьей подобласти на этой же поверхности (r=R2) также будет равен нулю.
Здесь же на границе раздела двух диэлектриков равны между собой нормальные составляющие векторов электрического смещения, а с учетом того, что в нашем случае вектор электрического смещения имеет одну составляющую, которая направлена по радиусу, то это означает, что на границе раздела равны между собой и сами векторы электрического смещения.
Перепишем последнее уравнение в следующем виде:
Решая совместно уравнения (1.42) и (1.43), находим постоянные интегрирования С3=-783.427, С4=-4008.
Таким образом, выражения для напряженности электрического поля и потенциала принимают вид
Потенциал в первой подобласти (внутри цилиндра) является величиной постоянной, равной значению потенциала со стороны второй подобласти на внутренней поверхности цилиндра.
График изменения потенциала и напряженности электрического поля представлен на рис. 1.28. Все значения на графике даны в относительных единицах. За базисное значение напряженности поля принято ее значение на наружной поверхности цилиндра Eb=130.6кВ/м. 
В качестве базисного значения потенциала принято абсолютное значение потенциала на расстоянии 0.01м от оси цилиндра Ub=400.2В.
Это же расстояние r=0.01м принято за базисное значение радиальной координаты.
Пример 3. Цилиндрический бесконечно длинный конденсатор заполнен двухслойным диэлектриком, относительные значения диэлектрической проницаемости слоев которого равны соответственно er1=2 и er2=4.
Радиус внутренней жилы равен R1=1мм, внутренний радиус наружной обкладки – R3=4мм, радиус поверхности раздела слоев диэлектрика – R2=2мм (рис. 1.29). К обкладкам конденсатора приложено постоянное напряжение Uо = 100 В. Один из диэлектриков заряжен (внутренний).
Объемная плотность заряда является функцией расстояния r от оси конденсатора r=аr 2 (а=10).
Определить закон изменения потенциала и напряженности электрического поля в каждом слое.
Построить графики изменения напряженности поля и потенциала вдоль радиуса.
Решение. В данной задаче поле так же является одномерным. Поэтому электрический потенциал в первом слое диэлектрика (R1?r?R2) удовлетворяет уравнению (1.26), а во втором слое (R2?r?R3) – уравнению (1.27). Эти уравнения имеют решения (1.28) и (1.30), соответственно. Перепишем их (при n=2) в следующем виде:
Для определения постоянных интегрирования С1, С2, С3, С4 поставим граничные условия.
Так, если принять потенциал наружного электрода равным нулю, то потенциал внутреннего электрода будет равен U0.


На границе раздела слоев диэлектриков (r=R2) равны между собой потенциалы и векторы электрического смещения (вектор электрического смещения имеет одну составляющую, направленную вдоль радиуса).
Решая систему уравнений, составленную из последних двух уравнений и уравнений (1.44) и (1.45) относительно постоянных интегрирования, получаем С1=-94.917, С2=-555.628, С3=-48.588, С4=-268.279.
Таким образом, выражения для напряженности электрического поля и потенциала принимают вид
Графики изменения данных функций вдоль радиуса представлены на рис. 1.30. 
Все значения на графике даны в относительных единицах. За базисное значение напряженности поля и потенциала приняты их значения на поверхности внутреннего электрода Eb=95.06кВ/м,
Ub=100В. За базисное значение радиальной координаты принят внутренний радиус наружного электрода R2.
Пример 4. Две протяженные проводящие пластины расположены в воздухе под углом a0=p/4 друг к другу и не соприкасаются (рис. 1.31). Напряжение между пластинами U0=100В.
Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Пренебрегая краевым эффектом, определить закон распределения потенциала и напряженности электрического поля между пластинами.
Поле между пластинами является одномерным (все величины зависят только от одной угловой координаты a цилиндрической системы координат). Потенциал, в этом случае, удовлетворяет уравнению (1.32) с решением (1.34).
Постоянные интегрирования определяются из граничных условий
Из данной системы уравнений определяем постоянные интегрирования С2=0, С1=U0/a0.
Таким образом, закон изменения искомых функций вдоль угловой координаты a цилиндрической системы координат можно окончательно представить следующим образом:
Как видно из последних выражений, эквипотенциальными поверхностями являются полуплоскости, проходящие через ось OZ и изолированными драг от друга, а линиями поля являются дуги окружностей с центром в начале координат.
Пример 5. Шар из диэлектрика (er = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k*r (k = 0,05p). Радиус шара R = 2см.
Рассчитать потенциал и напряженность электрического поля внутри и вне шара.
Данная задача была решена в примере 3 раздела 1.14 с помощью теоремы Гаусса.
Покажем, что этой же цели можно добиться и путем решения уравнений Пуассона (1.35) и Лапласа (1.36), которым удовлетворяет потенциал поля внутри и вне шара, соответственно.
Выражения, определяющие этот потенциал внутри (1.37) и вне шара (1.39), можно для данного случая представить в следующем виде:
Постоянные интегрирования определяются из известных граничных условий и с помощью некоторых физических соображений. Так, потенциал в центре шара (r=0) имеет конечное значение, поэтому постоянную С1 необходимо принимать равной нулю (С1=0). Далее, принимая потенциал равный нулю в точке, лежащей в бесконечности (r=?), получаем С4=0.
Оставшиеся две постоянные С2 и С3 определяем исходя из того, что на поверхности шара (r=R) равны между собой потенциалы и нормальные составляющие вектора электрического смещения
Перепишем данные граничные условия в следующем виде:
Решая совместно последние уравнения, находим постоянные интегрирования. C2=38460, С3=-709,964.
Подставляя значения этих постоянных в формулы для потенциалов, получаем
Отсюда видно, что данные выражения полностью аналогичны тем, которые были получены в примере 3 предыдущего раздела.
Пример 6. Две тонкие проводящие поверхности в виде коаксиальных конусов с изолированными вершинами расположены в воздухе. Потенциал первой поверхности U1=0, второй – U2=100В (рис. 1.32), q1=p/6, q2=2p/3.
Найти закон распределения потенциалов и напряженности электрического поля в пространстве между конусами.
Данная задача является одномерной, поскольку, в силу симметрии, решение для потенциала U зависит только от угла q. Поле в данном случае характеризуется уравнением (1.40) и имеет решение (1.41).
Исходя из заданных граничных условий составим уравнения для нахождения постоянных интегрирования С1 и С2

Таким образом, выражение для определения потенциала будет иметь вид
Напряженность электрического поля имеет одну составляющую
Эквипотенциальными поверхностями являются поверхности конусов с изолированными вершинами. При q=p/2 один из конусов переходит в плоскость. Линии поля лежат на меридианах.
📺 Видео
Задача Дирихле для круга. Уравнение ЛапласаСкачать

6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать

Метод Лапласа решения ДУСкачать

Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Уравнения математической физики. Уравнение Лапласа. Часть 1Скачать

7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать

Оператор Лапласа в полярных координатахСкачать

Локальная формула Муавра-ЛапласаСкачать

Решение уравнения Лапласа в шареСкачать

Оператор ЛапласаСкачать

Уравнение ЛапласаСкачать

Локальная формула ЛапласаСкачать