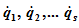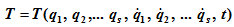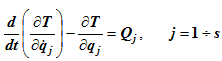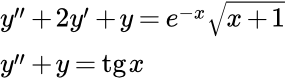Уравнение лагранжа 2 рода примеры решения

Видео:Уравнения Лагранжа второго родаСкачать

iSopromat.ru

Уравнения Лагранжа второго рода, которые представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат.

Для такой системы можно записать s уравнений, которые называются уравнениями Лагранжа второго рода или дифференциальными уравнениями движения в обобщенных координатах:

Уравнения Лагранжа второго рода могут быть обобщены на случай связей, осуществляемых с трением, хотя они и не являются идеальными. Для этого следует силу трения перенести из группы сил реакции в группу активных сил, тогда связь с трением можно формально считать идеальной.

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат q₁, q₂,…q_s.

Дважды интегрируя эти уравнения и определяя по начальным условиям постоянные интегрирования, получим систему уравнений движения в обобщенных координатах:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Уравнения Лагранжа второго рода. Задача 1Скачать

Примеры решений дифференциальных уравнений второго порядка методом Лагранжа

Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>> .

Видео:Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать

Пример 1

Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)

Шаг 1. Решение однородного уравнения

Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение второго порядка.

Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Варьируем постоянные C ₁ и C ₂ . То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .

Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;

.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .

Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .

Решение системы уравнений

Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.

Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .

Общее решение исходного уравнения:

;
.

Видео:Т. Уравнения Лагранжа 2 рода. Теория.Скачать

Пример 2

Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)

Шаг 1. Решение однородного уравнения

Решаем однородное дифференциальное уравнение:

(9)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Теперь варьируем постоянные C ₁ и C ₂ . То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .

Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .

Решение системы уравнений

Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.

Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :

.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.

Общее решение исходного уравнения:

.

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 19-06-2017

Видео:Составление уравнения Лагранжа. Задача о клинеСкачать

Применение уравнений Лагранжа второго рода к исследованию движения механической системы с одной степенью свободы

МИНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ

Видео:Система с двумя степенями свободыСкачать

Ростовский государственный университет

Видео:Уравнение ЛагранжаСкачать

П. Г. Иваночкин, Т. Я. Кожевникова, А. П. Сычев

Применение уравнений Лагранжа второго рода к исследованию движения механической системы с одной степенью свободы

Методические указания к выполнению

расчетно-графической работы Д7 по теоретической механике

Применение уравнений Лагранжа второго рода к исследованию движения механической системы с одной степенью свободы. Методические указания к выполнению расчетно-графической работы Д-7 по теоретической механике /П. Г. Иваночкин, Т. Я. Кожевникова, А. П. Сычев; Ростовский госуниверситет путей сообщения. Ростов-на-Дону, 2000, 19 с.

Кратко излагается теоретический материал, приводятся примеры решения типовых задач. Даны варианты к расчетно-графической работе Д7.

Одобрены к изданию кафедрой теоретической механики РГУПС и предназначены студентам механических специальностей.

Ил. 2 Библиогр.: 4 назв.

Рецензенты: канд. физ.-мат. наук, доц. А. И. Задорожный (РГУ); канд. техн. наук, доц. В. Г. Вильданов (РГУПС)

Иваночкин Павел Григорьевич

Сычев Александр Павлович

Методические указания к выполнению

Расчетно-графических работ Д7 по теоретической механике

Подписано в печать______2000г. Формат 60х84/16.

Бумага офсетная. Печать офсетная. Усл. печ. л 0,93.

Уч.-изд. л. 0,88. Тираж ____. Изд. № 000. Заказ № ____.

Ростовский государственный университет путей сообщения.

Ризография АСУ РГУПС. Лицензия ПДЛ №65-10 от 08.08.99г.

Адрес университета: 344038, г. Ростов н/Д, пл. им. Ростовского стрелкового полка народного ополчения,2

Ó Ростовский государственный университет путей сообщения, 2000

1. Общие указания

2. Задание Д7. Применение уравнений Лагранжа второго рода к исследованию движения механической системы с одной степенью свободы

3. Условие задачи Д7

4. Указания к решению задачи

5. Примеры решения типовых задач

6. Данные к вариантам задания Д7

7. Схемы к вариантам задания Д7

В первой части методических указаний содержатся краткие сведения из теории и примеры решения задания Д7, входящего в курсовую работу по теоретической механике.

В приложении I студент выбирает свой вариант по номеру рисунка согласно цифре, под которой его фамилия стоит в учебном журнале. Исходные данные берутся из таблицы (приложение 2). Номер строки в ней для каждой группы назначает преподаватель.

Оформление отчета

Расчетно-графическая работа оформляется в такой последовательности:

— условие задачи с рисунком;

На отдельном листе нужно полностью переписать условие задачи и выполнить относящийся к ней рисунок. Он должен быть выполнен четко, аккуратно, карандашом. В работе надо оставлять поля для замечаний консультанта.

Решение каждой задачи следует сопровождать пояснениями, то есть надо указывать, какие теоремы, формулы или уравнения применяются для решения. Чертежи, выполняемые в процессе решения задачи, должны соответствовать конфигурации системы в рассматриваемый момент времени, на них должны изображаться все векторы (силы, ускорения). Формулы сначала надо написать в общем виде (буквенном), а затем подставлять числовые значения, рядом указывать единицы измерения. В конце расчета дается сводная таблица полученных результатов.

Порядок приема и сдачи индивидуального задания

I. Срок сдачи индивидуального задания указывается консультантом (руководителем практических занятий).

II. При защите расчетно-графической работы студент должен пояснить ход ее выполнения, ответить на все поставленные вопросы и в отдельных случаях решить предложенные ему примеры.

III. Работа, небрежно выполненная и содержащая орфографические ошибки, не принимается.

Задание не засчитывается, если указанные требования не выполнены!

Задание Д7. Применение уравнений Лагранжа второго рода к исследованию движения механической системы с одной степенью свободы

Краткие сведения из теории к заданию

Уравнения Лагранжа второго рода представляют собой систему уравнений динамики в обобщенных координатах. Использование их является универсальным методом получения системы дифференциальных уравнений, описывающих движение любой механической системы

Обобщенными координатами системы называется совокупность независимых параметров, которые при наименьшем числе однозначно определяют положение механической системы.

В последующем обобщенные координаты обозначаются q1, q1,…, qN или qj(j=1,2,…,N). Производные по времени от обобщенных координат называются обобщенными скоростями . Число N независимых обобщенных координат голономной системы равно числу ее степеней свободы.

Уравнения Лагранжа второго рода имеют вид

где Т — кинетическая энергия системы;

Qj — обобщенная сила, соответствующая j-той обобщенной координате.

Кинетическая энергия системы равна сумме кинетических энергий всех объектов, образующих систему.

Кинетическая энергия твердого тела определяется по формулам:

— при поступательном движении

,

Vс – скорость центра масс тела;

,

Jz – момент инерции тела относительно оси вращения;

w — угловая скорость вращения;

— при плоскопараллельном движении

,

Jzc – момент инерции тела относительно оси, проходящей через центр масс, перпендикулярно плоскости движения.

Величина называется j-той обобщенной силой.

Если вычислить сумму элементарных работ активных сил, действующих на точки системы на возможном перемещении системы, то соответствующая формула может быть представлена в виде

поэтому часто обобщенные системы определяют как коэффициенты, стоящие в выражении суммы элементарных работ активных сил при соответствующих обобщенных возможных перемещениях.

Для определения обобщенной силы, соответствующей j-той обобщенной координате, необходимо этой координате сообщить приращение , оставляя все остальные обобщенные координаты без изменений; вычислить сумму элементарных работ всех сил, действующих на систему, на этом перемещении и полученную работу разделить на приращение обобщенной координаты

При вычислении работы сил используются следующие формулы:

— работа сил тяжести

,

h – изменение высоты между начальным и конечным положениями

— работа силы трения

— работа постоянной силы на прямолинейном перемещении

,

a — угол между направлением силы и направлением перемещения

— работа сил, приложенных к вращающемуся телу

,

Mz(F) – момент силы относительно оси вращения;

j — угол поворота тела

Методика составления уравнений Лагранжа второго рода

Составление уравнений Лагранжа второго рода производится в следующем порядке:

1) определяется число степеней свободы заданной механической системы;

2) выбираются независимые обобщенные координаты, число которых равно числу степеней свободы;

3) вычисляется кинетическая энергия Т рассматриваемой системы, которая выражается через обобщенные скорости;

4) находятся частные производные кинетической энергии по обобщенным скоростям, т. е.

затем вычисляются их производные по времени

5) определяются частные производные кинетической энергии по обобщенным координатам

6) находятся обобщенные силы Q1, Q2,…QN соответствующие выбранным обобщенным координатам;

7) полученные в п. п. 4-6 результаты подставляются в уравнения Лагранжа.

Условие задачи Д-7

Механическая система состоит из ступенчатых шкивов 1 и 2 весом Р1 и Р2 с радиусами R1=R, r1=0,4R и R2=R, r2=0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу); грузов или сплошных однородных цилиндрических катков 3, 4, 5, веса которых Р3, Р4, Р5 соответственно. Тела системы соединены нитями, намотанными на шкивы и невесомые блоки. Участки нити параллельны соответствующим плоскостям. Грузы скользят по плоскостям без трения, а катки катятся без скольжения. Система движения в вертикальной плоскости под действием сил тяжести, кроме того, на одно из тел действует постоянная сила F, а на шкивы 1 или 2 при их вращении действуют постоянные моменты сил сопротивления М1 и М2.

Определить величину, указанную в таблице в столбце «Найти», где e1 и e2 — угловые ускорения шкивов 1 и 2, аС3, аС4, аС5 — ускорения грузов или центров масс соответствующих катков. (Если необходимо определить e1 или e2 принять R=0,25м).

Указания к решению задачи

Для исследования движения системы нужно составить уравнение Лагранжа 2-го рода. Во всех вариантах система имеет одну степень свободы, и еe положение определяется одной обобщенной координатой q. Уравнение Лагранжа — это дифференциальное уравнение 2-го порядка относительно обобщенной координаты.

(1)

Если нужно найти ускорение a3C или a4C грузов 3,4 или ускорение a5C центра масс С катка 5, то за обобщенную координату целесообразно принять перемещение х центра масс этих тел, тогда — обобщенная скорость и уравнение примет вид:

(2)

Если же нужно определить угловое ускорение e1 или e2 одного из шкивов, то за обобщенную координату нужно принять угол поворота шкива, т. е. и уравнение будет иметь вид:

(3)

Для составления уравнения (2) или (3) нужно вычислить кинетическую энергию Т системы, выразив её через обобщенную скорость ( или ) и обобщенную координату q (x или j). Затем нужно найти обобщенную силу Qx или Qj, для определения которой нужно сообщить системе возможное (малое) перемещение ( или ) и вычислить сумму элементарных работ всех сил на этом перемещении. Элементарные перемещения всех тел нужно выразить через dx или dj , тогда получим: или , т. е. коэффициенты при dx или dj в выражении dА и будут обобщенными силами.

Примечание: в варианте №21 шкивы 1, 2 и в варианте №25 шкив 2 считать однородными цилиндрами.

Примеры решения типовых задач

Дано: Р1=12Р, Р2=8Р, Р3=2Р, Р4=12Р, Р5=6Р, F=3P, M=3PR

(Р-в Н, R-в м.), R1=0,3R, r1=0,2R, R2=0,2R, r2=0,1R.

1. Система имеет одну степень свободы. За обобщенную координату возьмем перемещение груза 4 (q=x).

Предположим, груз 4 опускается. Составим уравнение Лагранжа 2го рода:

(1)

2. Определим кинетическую энергию Т системы:

(2)

Шкивы 1 и 2 вращаются вокруг неподвижной оси, грузы 3 и 4 движутся поступательно, а каток 5 движется плоскопараллельно.

(3)

(4)

3. Скорости n3 и nс, угловые скорости w1, w2 и w5 выразим через обобщенную скорость

(5)

Подставляя значения (4) и (5) в равенства (3), а затем в (2), получим:

Найдем частные производные от Т по х и :

(7)

4. Определим обобщенную силу Qх. На чертеже покажем силы, совершающие при движении системы работу, т. е. силы тяжести , и момент пары силы М(сила работы не совершает, т. к. груз 3 движется по горизонтали).

Сообщим системе возможное перемещение dх груза 4 в направлении его движения и покажем перемещения остальных тел: груза 3-dх3, центра масс С катка 5-dхс, а для шкивов углы поворота dj1 и dj2. Вычислим сумму элементарных работ сил тяжести , , силы и момента пары сил М на этих перемещениях.

Коэффициент при dх в выражении dА будет обобщенной силой Qх.

5. Найденные величины (7) и (8) подставим в уравнение (1).

Отсюда находим:

Ответ:

Дано: Р1=2Р, Р2=0, Р3=3Р, Р4=0, Р5=4Р, F=12Р, М1=0,3РR, М2=0

R1=R, R2=R, r1=0,4R, r2=0,8R, R=0,25м, a=60°, b=30°

Найти: e2 – угловое ускорение второго шкива

1. Система имеет одну степень свободы. За обобщенную координату возьмем угол поворота шкива 2 (q=j). Предположим, что шкив вращается против часовой стрелки. Составим уравнение Лагранжа 2го рода:

(1)

2. Определим кинетическую энергию Т системы

(2)

Грузы 3 и 4 движутся поступательно, следовательно

Шкивы 1 и 2 вращаются вокруг неподвижных осей, следовательно

Каток 5 движется плоскопараллельно

3. Скорости V3, V4, VС, угловые скорости w1, w5 выразим через обобщенную скорость

Из рисунка видно, что

(точка Р касания катка и наклонной плоскости является мгновенным центром скоростей катка)

Подставим найденные выражения в формулу кинетической энергии системы

4. Определим обобщенную силу Qj. На чертеже покажем силы, совершающие при движении системы работу, т. е. силы тяжести , , и моменты пары сил М1 и М2 (силы и приложенные к осям вращения шкивов работы не совершают).

Сообщим системе возможное перемещение соответствующее повороту шкива 2 на угол против часовой стрелки и покажем перемещения остальных тел: груза 3 — , груза 4 — , центра масс С кат-ка 5 — , а для шкива 1 – угол поворота .

Вычислим сумму элементарных работ указанных активных сил (силы тяжести сила и пара сил с моментом М) на выбранном возможном перемещении системы

,

Вычислим обобщенную силу Q по формуле

Подставляя все полученные выражения в уравнение Лагранжа получим его в виде

📽️ Видео

Уравнение Лагранжа 2-го рода. ЗадачаСкачать

Уравнение Лагранджа II рода - ч.1 - решениеСкачать

Решение уравнения ЛагранжаСкачать

Уравнение Лагранжа 2-го рода. Линейная координатаСкачать

№1. Уравнения Лагранжа 2 рода. Задача 1.Скачать

Уравнение Лагранжа 2-го рода для механизма с одной степенью свободыСкачать

Составляем уравнение ЛагранжаСкачать

§5.5. Уравнения Лагранжа второго родаСкачать

Уравнение ЛагранжаСкачать

Уравнение Лагранжа 2-го рода. ЗадачаСкачать

Решаю задачу на тему Уравнение Лагранжа 2 родаСкачать

Вывод уравнения Лагранжа 2-го родаСкачать

№4. Уравнения Лагранжа 2 рода. Задача 4.Скачать