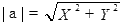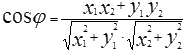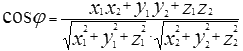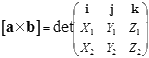Уравнение квадрата на координатной плоскости для программирования

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Видео:Уравнение окружности, строим на координатной плоскостиСкачать

Уравнение квадрата в декартовой системе координат.

Проанализируем расположение квадрата на координатной плоскости.

В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:

где точка О`(a;b) – точка пересечения диагоналей квадрата;

d – длина диагонали квадрата.

В частном случае, когда точка О(0;0) — начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:

где d– длина диагонали квадрата.

Видео:Уравнение окружности (1)Скачать

Вычислительная геометрия

Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач [1]. При программировании решений к задачам на геометрию требуется своя специфика. Хорошей литературы на эту тему не так уж много, но все-таки несколько источников указать можно [2], [3], [4].

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Основные геометрические понятия

Системы координат и векторы

Положение любой точки $P$ в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат. Числа, определяющие положение точки, называются координатами этой точки. Наиболее употребительные координатные системы — декартовы прямоугольные. Кроме прямоугольных систем координат существуют косоугольные системы. Прямоугольные и косоугольные координатные системы объединяются под названием декартовых систем координат.

Иногда на плоскости применяют полярные системы координат, а в пространстве — цилиндрические или сферические системы координат.

Для задания декартовой прямоугольной системы координат нужно выбрать несколько взаимно перпендикулярных прямых, называемых осями. Точка пересечения осей O называется началом координат. На каждой оси нужно задать положительное направление и выбрать единицу масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P.

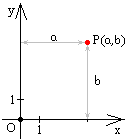
Когда говорят про двухмерную систему координат, горизонтальную ось называют осью абсцисс (осью Ox), вертикальную ось — осью ординат (осью Оy). Положительные направления выбирают на оси Ox — вправо, на оси Oy — вверх. Координаты x и y называются соответственно абсциссой и ординатой точки. Запись P(a,b) означает, что точка P на плоскости имеет абсциссу a и ординату b (рис.1).

Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до трех взаимно перпендикулярных координатных плоскостей. В зависимости от взаимного расположения положительных направлений координатных осей возможны левая и правая координатные системы.

Отрезок, концы которого упорядочены (рис.2), называется направленным (упорядоченность означает, что один конец отрезка считается начальной точкой, а другой – конечной).

Направленный отрезок называется вектором.

Длина вектора называется его модулем:
| a | – обозначение модуля вектора a.

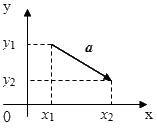
Проекции вектора a с начальной точкой (X₁, y ₁) и конечной точкой (X₂, 2) на оси координат называются координатами вектора: a =<X₂ – X₁, Y₂ – y₁> или a(X, Y). Модуль вектора через его координаты:

Два вектора считаются равными, если они имеют одинаковую длину и направление (равенство соответствующих координат), следовательно, алгебраическое представление вектора — это упорядоченный набор чисел (его координаты). Сложение и вычитание векторов a(X₁,Y₁) и b(X₂, Y₂), умножение вектора на число t определяются по следующим правилам:

Вектора, отличающиеся множителем, называются коллинеарными.

4.1.2. Скалярное и векторное произведение

Скалярное произведение двух векторов – это число, равное произведению модулей этих векторов на косинус угла между ними (a, b) = |a|·|b| cos φ.

Следствие. Если два вектора перпендикулярны, то их скалярное произведение равно нулю.

Угол между векторами – это наименьший угол между направленными отрезками, приведенными к одной начальной точке (рис. 3).

1. Если угол φ — острый, то (a, b)>0.

2. Если угол φ — тупой, то (a, b) (a, a) = |a| 2 .

Из определения скалярного произведения можно найти косинус угла, выраженный через координаты векторов.

Следствие. Вектор b(Y, —X) будет перпендикулярен вектору a(X, Y).

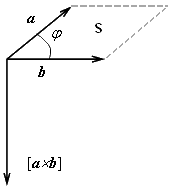
Векторное произведение двух векторов – это вектор, обозначаемый [a × b], который определяется следующими условиями:

1. длина вектора |[a× b trong>a|·|>|· sinφ; где & между векторами (т.е. равна S параллелограмма, построенного на сторонах a и b);
2. [a×b] вектор перпендикулярен ка i>a, так и вектору ng>;
3. [a×b] направлен как ось oz к осям >ox и oy , ктора a, b и [a× >b] образуют правую тройку (по правилу “буравчика”, если вектор a поворачивать до вектора bпо i>

Векторное произведение геометрически представлено на рис.4.

Векторное произведение двух векторов через координаты выражается следующим образом:

[a × b ] = (Y₁ · Z₂ — Y₂ &#1 > Z ₁ ) g> i + (Z₁ · > X₂ — Z ₂ · > X ₁ ) Symbol’>× span> (X_{1 183;Y 2 — X >· /i> 1 ) × k и yle=»float:left;margin:10px 10px 0 0;»>}

где /strong>, j, k ые вектора осей OX >OY , OZ соответственно; det (…) – означает определитель матрицы, составленной из орт осей и координат исходных векторов.

Если плоскость исходных векторов взять за плоскость XY , то в формулах координаты Z₁ и Z₂ равны нулю xt-indent:20pt’>Следует обратить внимание на многозн веденных геометрических понятий, которые можно использовать в различных задачах. Например, для понятия векторное произведение:

• длина результирующего вектора определяет площадь параллелограмма, построенного на заданных векторах;
• нулевое значение длины — параллельность векторов;
• результирующий вектор определяет нормаль к плоскости заданных векторов;
• его направление означает, что один вектор расположен «слева» или «справа» относительно другого.

4.1.3. Уравнения прямой и окружности на плоскости

a) Через заданную на плоскости точку с координатами (X₀, y ₀) можно провести прямую, перпендикулярную вектору $n$(a,b). Для любой точки на этой прямой с координатами (X,Y) направляющий вектор a = <X – X y – y₀> перпендикулярен вектору нормали $n$, т.е. скалярное произведение ($n$, a i>= 0 или A(X – X₀) + B( sp;– y₀) = 0. Раскрывая скобки, легко получить классическое уравнение прямой Ax + By + C = 0, где константа C > = -A X₀ -B y₀.

c) Уравнение прямой, проходящей через две ра рдинатами (X₁, & ub>1) и (X₂, >y ₂), выражается следующей формулой:

d) font:7.0pt «»‘> Уравнение прямой в парам ается системой уравнений

Эта же система может задавать и отрезок при t ∈ [0, 1], и луч при >t ∈ [0, >].

style=’ font:7.0pt «»‘> Уравнения окружности в параметрическом виде выглядят так:

Видео:Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

4.2. Отношения между геометрическими объектами

4.2.1. Расстояние и площадь

a) Расстояние d между двумя точками с координатами (X₁, Y₁) >X₂, y i>) вычисляется по формуле 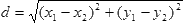=»float:left;margin:20px 10px 0 0;»>

span style=’ font:7.0pt «»‘> Расстояние d от точки P ₁(X₁, Y₁) до прямой Ax + By + C = 0 вычисляется следующим образом.

Предположим, что выбрана точка P ₀(X₀, y ₀), лежащая на прямой (рисунок 5), тогда проекция отрезка P ₁ P ₀ на вектор n (a, b). Используя формулы скалярного произведения и свойство Ax₀ + By₀ + C = 0, получим: mg src=»https://lisiynos.github.io/s3/geom0/12.pn%20%3E,%20%D0%B8%D0%BB%D0%B8%20%D0%BE%D0%BA%D0%BE%D0%BD%D1%87%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%20%3Csub%3E%3Cimg%20src=»https://lisiynos.github.io/s3/geom0/13.png» /> ,

причем, если убрать знак модуля из числителя, то получится ориентированно вающее на расположение точки относительно прямой.

c) bsp; Вычисление расстояния d X₁, Y₁) до луча или отрезка отличается от вышеописанного, так как основание перпендикуляра, опущенного из точки на продолженную прямую, может не лежать на луче/отрезке. В этом случае кратчайшим расстоянием будет дистанция от точки до начальной точки луча или одной из начальных точек отрезка.

d) Площадь треугольника со сторонами a, b, c по формуле Герона 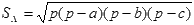, где p – полупериметр треугольника.

e) Площадь треугольника со сторонами a, b и углом между ними φ вычисляется как половина площади параллелограмма, построенного на этих сторонах, с использованием формулы векторного произведения.

Видео:Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать

Площадь произвольного многоугольника

f) Площадь произвольного многоугольника вычисляется как сумма ориентированных площадей треугольников, у которых одна вершина – начало координат, а две другие – пары вершин многоугольника (последов сторон).

t;’> , где S_{i > – площадь i ника, $n$ – количество вершин многоугольника. Площади треугольников в следующим формулам:}

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Параллельность, перпендикулярность, пересечение

Для того елить, принадлежит ли точка прямой, необходимо подставить координаты точки в уравнение прямой. При определении принадлежности точки отрезку добавляется проверка на то, лежат ли координаты точки между коорди конца отрезка.

Определение того, пересекают е, заданные уравнениями
sub>x + B₁y + C₁ = 0 и A_{2 + B 2}y > = 0, сводится к следующему:

Взаимное расположение двух отрезков можно проверить с помощью четырех векторных произведений (рис. 6).

Отрезки пересекаются, если одновременно выполняются два условия: V ₁ V ₂ V ₁ и V ₂ разных знаков), V ₃ V ₄ V ₃ V ₄ разных знаков). Если V ₁ V ₂>0 или V _{span >V 4>0}, то отрезки не пересекаются.

Дополнительные проверки используются, если точка пересечения лежит на одном из отрезков.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

снаружи

Чтобы определить, находится ли точка внутри или снаружи многоугольника, необходимо знать, является ли многоугольник выпуклым или нет.

Для выпуклого N-угольника существует несколько способов определения принадлежности точки многоуго le=’margin: 0cm -.25pt 0cm 36.0pt;text-indent: -18.0pt’>1) sp; Вычислить сумму площадей треугольников, образованных смежными сторонами многоугольника и заданной точкой, используя форм ь с площадью многоугольника, вычисленной по векторному произведени 1. Если площади равны (или отличаются не более чем на заданную малую величину), то точка внутри многоугольника.

: -18.0pt’>2) Пров и данная точка лежат в одной полуплоскости от каждой стороны N-угольника, то точка внутренняя. В уравнение прямой через каждые две соседние вершины x_i , y _i и X_i+1, y _i+1, подставляем координаты данной точки X,Y и по очереди координаты всех остальных вершин. Другими словами, необходимо, чтобы полученные значения функции F ( x_i , y _i,X_i+1, y _i+1,X, y ) = (X_i+1—X_i)( y —Y_i)-(X-X_i)( y _i+1—Y_i) при разных x_i , y _i, X_i+1, y _i+1 ( i = 1, …, N -1) были одног а внутри многоугольника.

: -18.0pt’>3) Составить N векторны н вектор — сторона многоугольника, а второй вектор — из точки до одной из вершин на стороне) и проверить, все ли они одного знака (если одного, то точка внутри).

Для про N-угольника все эти способы работают не всегда. Необходимо щие способы:

-18.0pt’>4) nbsp; Проверить, чему равна сумма углов вокруг исследуемой точки, то ов, под которыми видна каждая сторона многоугольника из искомой точки. Причем у о знаком, соответствующим последовательному обходу сторон многоугольника. Знак угла определяется векторным произведе торов от заданной точки до вершин многоугольника, определяющих сторону. еляется по формуле арккосинуса для найденного из скалярного произведения косину внутренняя, то сумма углов по модулю — 2 pan>, если наружная, то ноль. В программе достаточно произвести сравнение абсолютной величины суммарного угла с p (больше либо меньше π).

5) Провести через точку произвольную прямую. Если она не пересекает ни одну из сторон многоугольника, то точка лежит снаружи. Если пересечения есть, то определить количество пересечений луча, выходящего из данной точки в любую сторону, со сторонами многоугольника. Точка внутри, если количество пересечений нечетно.

Видео:Видеоурок "Координатная плоскость, координата точки"Скачать

4.3. Построение выпуклой оболочки

Выпуклой оболочкой множества точек на плоскости является выпуклый многоугольник с вершинами из точек заданного множества. Существует несколько алгоритмов построения выпуклой оболочки. Самыми простыми для реализации являются алгоритмы Джарвиса и Грэхема.

Идея алгоритма Джарвиса построения выпуклой оболочки (его называют еще алгоритмом «заворачивания подарка») заключается в следующем:

1. Ищется точка с минимальной координатой по оси OX . От нее задается первоначальное вертикальное направление.

2. По очереди, перебирая все остальные точки, ищется такая, чтобы вектор с концом в этой точке, а началом в исходной образовал с первоначальным вектором минимальный угол. Найденная таким образом точка будет точкой из выпуклой оболочки.

3. Найденная точка принимается за исходную, новый построенный вектор задает исходное направление и из оставшихся N -2 точек ищется следующая точка.

4. Процесс продолжается до первоначальной выбранной точки.

Идея алгоритма Грэхема построения выпуклой оболочки заключается в следующем:

1. Найти левую верхнюю точку. Запомнить ее.

2. Отсортировать все остальные точки по возрастанию угла в полярной системе координат с центром в запомненной точке.

3. По очереди перебирая все отсортированные точки, исключать те, которые будут содержаться внутри выпуклой оболочки. Оставшиеся при таком отборе точки и составят выпуклую оболочку.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

4.4. Задачи с использованием геометрических понятий

При решении геометрических задач скалярное произведение векторов используется для определения угла (или косинуса угла) между векторами (для проверки перпендикулярности векторов, для определения наибольшего или наименьшего угла).

Векторное произведение двух векторов позволяет определить ориентацию одного объекта относительно другого (по одну сторону или по разные, внутри или снаружи), а также направление движения (влево или вправо, вниз или вверх, по часовой стрелке или против часовой).

4.4.1. Примеры решений

Задача 1. Мэрия решила выделить деньги на постройку кольцевой автодороги вокруг города. Координаты всех домов в городе заданы парой целых чисел на плоскости.

Уровень 1. Описать алгоритм построения дороги минимальной длины в виде отрезков, соединяющих точки-дома, вдоль которых должна пройти дорога при условии, что внутри дороги окажутся все остальные дома города.

Можно использовать алгоритм Джарвиса построения выпуклой оболочки:

1. Найти точку с минимальной координатой по оси OX . Запомнить ее.

2. Построить вектор, задающий первоначальное вертикальное направление (за начало вектора можно взять найденную точку).

3. В цикле перебирая все остальные точки, найти такую, чтобы вектор с концом в этой точке, а началом в исходной образовал с первоначальным вектором минимальный угол (минимальному углу соответствует максимальный косинус, который определяется из формулы скалярного произведения). Найденная таким образом точка будет точкой из выпуклой оболочки.

4. Найденную точку принять за исходную, новый построенный вектор принять за исходное направление и из оставшихся N -2 точек искать следующую точку по принципу, изложенному в предыдущем пункте.

5. Процесс прекратить, когда дойдем до первой выбранной точки или переберем по количеству N точек (предотвращение зацикливания).

Уровень 2. Написать программу, которая выводит в файл координаты домов, вдоль которых должна пройти кольцевая автодорога.

Количество домов N (3 N N -го дома X_N Y_N (2 числа через пробел)

Координаты 1-го дома X₁ Y₁ (2 числа через пробел)

Координаты K -го дома X_K Y_K (2 числа через пробел)

Входные данные : Выходные данные :

Программа 1.1 ( на языке QBasic) :

OPEN “INPUT.TXT” FOR INPUT AS #1

TXT” FOR OUTPUT AS #2

DIM x(1 TO n), y(1 TO n) ‘ координаты n точек

FOR i = 1 TO n style=’margin: 0cm 1.0cm 0cm 20.7pt;text-indent:20pt’> INPUT #1, x(i), y(i)

right:1.0cm;text-indent: 19.85pt’> NEXT

чки с минимальной координатой x

‘ n1- номер на x1,y1- координаты найденной точки

x1 = x( i1 = 1: n1 = 1

19.85pt’> PRINT #2, x1, y1

m;text-indent: 19.85pt’> NEXT

X0 = X1: y 0 = Y1 – 1 ‘ взяли вспомогательную точку (x0, y0)

mcos = ‘ число, необходимое для поиска максимального cos,

‘ т.е. минимального угла

‘>X10 = X1 — X0: Y10 = Y1 — Y0 ‘ строим вектор а

a = SQR (X10 ^ 2 + Y10 ^ 2) ‘ находим |a|

xi1 = x(i) — x1: yi1 = y(i) — y1 ‘ вектор b

1 ^ 2 + yi1 ^ 2) ‘ |b|

cosa = (X10 * xi 1 + Y10 an>1) / (a * b) ‘ cos угла из скалярного

IF cosa > mcos THEN mcos = cosa: nomi = i

IF nomi = n1 THEN END

x0 = x1: y0 = y1 ‘ за вектор а берем b

pt;text-indent:20pt’> x1 = x(nomi): y1 = y(nomi)

ext-indent:20pt’> PRINT #2, x1, y1

0cm 1.0cm 0cm 20.7pt;text-indent:20pt’> i1 = nomi

pt’> LOOP UNTIL k > n – 1

Уровень 3. Смоделировать ора решение задачи, изобразив каждый из домов в виде точки или о диуса. Изобразить построение кольцевой автодороги минимальной длины в виде замкнутой ломаной. Возможно использование для задания экранных координат точек датчика случайных чисел. Исследовать пр я выпуклой оболочки при малом и большом количестве точек. Сравнить процесс построения двумя разными алгоритмами (Джарв ма).

Программа 1.3 (на языке pan>) :

SCREEN ‘программа с графическим оформлением

t-indent: 19.85pt’> INPUT » Количество точек — «, n

.0cm;text-indent: 19.85pt’> RANDOMIZE TIMER

;text-indent: 19.85pt’> DIM x(1 TO n), y(1 TO n)

ext-indent: 19.85pt’> FOR i = 1 TO n

>x(i) = INT(RND * 600 + 20)

>y(i) = INT(RND * 300 + 20)

ndent:20pt’> CIRCLE (x(i), y(i)), 3

IF n = 1 THEN END

x1 = x(1): y1 = y(1): i1 = 1: n1 = 1

x0 = x1: y0 = y1 – 1

x10 = x1 — x0: y10 = y1 — y0

a = SQR(x10 ^ 2 + y10 ^ 2)

pt’> IF i i1 THEN

>xi1 = x(i) — x1: yi1 = y(i) — y1

>b = SQR(xi1 ^ 2 + yi1 ^ 2)

cosa = (x10 * xi1 + y10 * yi1) / (a * b)

IF cosa > mcos THEN mcos = cosa: nomi = i

LINE (x1, y1)-(x(nomi), y(nomi))

IF nomi = n1 THEN END

x0 = x1: y0 = y1 tyle=’margin: 0cm 1.0cm 0cm 20.7pt;text-indent:20pt’> x1 = x(nomi): y1 = y(nomi)

rgin: 0cm 1.0cm 0cm 20.7pt;text-indent:20pt’> i1 = nomi

pt’>Задача 2. «Штраф за левые повороты». Новый градоначальник города с целью пополнения бюджета и экономии горючего провести кампанию борьбы с “левым” уклоном. Д ретил водителям выполнять левые повороты, установив за каждый поворот налево штраф в 1 млн. рублей (прейскурант тяжелого прошлого Глупову достались улицы, которые могут пересекаться под любыми углами. Градоначальник приказал установить компьютерную систему слежки за автомобилями, которая фиксирует координаты каждого автомобиля в начале движе ижения и во время поворота.

Уровень 1. Описа исления штрафа водителю автомобиля, если задана последовательность координат движ мобиля.

Поворот считается левым, если направление текущего отрезка траект >a2 относительно направления предыдущего отрезка a1 меняется по на в левую сторону (поворот против часовой стрелки). А это означает, что векторное прои ов [a1 × a2] авилу «буравчика»).

1. &nbsp Из координат первых трех точек в заданной последовательности определить два вектора ng> и a2.

. Составить их векторное произведение.

3. Если [a1 × a2] > 0, то увеличить счетчик для подсчета левых поворотов на 1.

4. Переопределить данные, взяв за вектор a1 вектор a2.

5. Определить вектор a2, взяв координаты следующей точки в последовательности.

6. Повторить процесс с пункта 2.

7. После перебора всех точек значение счетчика будет содержать ответ задачи.

Уровень 2. Написать программу, вычисляющую штраф водителю автомобиля, если задана последовательность координат движения этого автомобиля.

Координаты начала движения X₀ Y₀ (2 числа через пробел)

Координаты первого поворота X₁ Y₁ (2 числа через пробел)

Координаты N -го поворота X_N Y_N (2 числа через пробел)

Координаты конца движения X _{N +1} Y_{N +1} (2 числа через пробел)

💡 Видео

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Расстояние между двумя точками (прямоугольная система координат на плоскости).Скачать

ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Уравнение окружностиСкачать

Координатная плоскость. Часть 1 #shortsСкачать

Метод координат для ЕГЭ с нуля за 30 минут.Скачать