Уравнение кулона для глинистых грунтов (5 видео)

Закон Кулона для связных и несвязных грунтов.

Грунты оснований зданий и сооружений испытывают воздействие не только нормальных, но и касательных напряжений. Когда касательные напряжения по какой-либо поверхности в грунте достигают его предельного сопротивления, то происходит сдвиг одной части массива грунта по другой.

Сопротивлений грунта сдвигу характеризуется его прочностными свойствами и используется в расчетах оснований по первому предельному стоянию (прочности).

Прочностью грунта называют способность его воспринимать силы внешнего воздействия, не разрушаясь. Прочность грунта определяется его сопротивляемостью сдвигу и оценивается показателем, который называется предельным сопротивлением сдвигу .

Внутренним сопротивлением, препятствующим сдвигу частиц, в песчаных грунтах будет лишь трение, возникающее в точках контакта частиц. В связных же грунтах перемещению частиц будут сопротивляться внутренние структурные связи.

Предельное сопротивление грунтов сдвигу может быть установлено по испытанию его образцов на прямой плоскостной срез, трехосное сжатие, по результатам среза грунта крыльчаткой и др. способами. При испытаниях на прямой плоскостной срез используют односрезный прибор. При этом цилиндрический образец грунта помещают в срезыватель так, чтобы одна его половина оставалась неподвижной, а другая могла перемещаться горизонтально под действием сдвигающей нагрузке. К образцу прикладывается так же вертикальная сжимающая нагрузка.

Рис.10. Схема сдвигового прибора.

Многочисленными экспериментами установлено, что график зависимости предельного сопротивления сдвигу сыпучих грунтов от давления представляет собой прямую, исходящую из начала координат и наклоненную под углом φ к оси давлений.

Рис.11. График сопротивления сдвигу сыпучего грунта.

Эта зависимость может быть выражена уравнением:

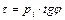
где φ – угол внутреннего трения грунта.

Это и есть закон Кулона для сыпучих грунтов (1773 г.) — предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению.

Основными видами испытаний связных грунтов на сдвиг будут испытания по закрытой (неконсолидированные испытания) и открытой (консолидированные) системам. Испытания грунтов по первой схеме выполняются таким образом, что плотность и влажность грунта в процессе опыта не меняются, и поэтому такие опыты носят название быстрого сдвига. Испытания по открытой схеме производят после предварительного уплотнения образцов вертикальной нагрузкой до стабилизации осадки, а горизонтальное усилие на образец передается ступенями, при этом каждая ступень выдерживается до стабилизации горизонтальной деформации. Испытания сыпучих грунтов производят по первой схеме, а связных по второй.

Диаграмма испытания глинистых грунтов на сдвиг приведена на рис.12.

Рис.12. График сопротивления сдвигу связного грунта.

Опыты показывают, что диаграмму консолидированного сдвига глинистых грунтов, несмотря на кривизну начального участка, без особых погрешностей можно описать уравнением прямой линии:

Это уравнение выражает закон Кулона для связных грунтов: предельное сопротивление связных грунтов сдвигу при завершенной консолидации есть функция первой степени от нормального давления.

Т.о. для связных грунтов сопротивление сдвигу характеризуется двумя параметрами: углом внутреннего трения φ и удельным сцеплением с. Если прямую аb продлить влево до пересечения с осью абсцисс, то она отсечет на ней отрезок р_ε. Величину р_ε – называют давлением связности. Используя это давление, параметр сцепления (связности) грунта можно представить в виде:

Характеристики сопротивления грунтов сдвигу могут быть так же определены по результатам опытов на трехосное сжатие. Прибор для таких испытаний называется – стабилометром.

Т.о., для расчета оснований зданий и сооружений необходимо определить вышеуказанные прочностные характеристики, а именно: угол внутреннего трения и удельное сцепление грунта.

Содержание

Лекция 2. ПРЕДЕЛЬНОЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ. УСЛОВИЕ ПРОЧНОСТИ ГРУНТА (ЗАКОН КУЛОНА)
Скачать:
в рамках общей темы «Основные закономерности механики грунтов»
НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТА
ВНУТРЕННЕЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ
МЕТОД ОПРЕДЕЛЕНИЯ ПРОЧНОСТНЫХ ХАРАКТЕРИСТИК ГРУНТА
УСЛОВИЕ ПРОЧНОСТИ ДЛЯ СЫПУЧИХ И СВЯЗНЫХ ГРУНТОВ
Расчеты грунтов по модели Кулона-Мора
📹 Видео

Видео:6,6Скачать

Лекция 2. ПРЕДЕЛЬНОЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ. УСЛОВИЕ ПРОЧНОСТИ ГРУНТА (ЗАКОН КУЛОНА)

Скачать:

Видео:Лекция №4. Испытания грунтов в условиях 3 х-осн. сжатия.Скачать

в рамках общей темы «Основные закономерности механики грунтов»

Основные показатели грунтов, используемые при расчётах предельной прочности и устойчивости грунтов, а также при расчете давления грунтов на ограждения могут быть получены в результате изучения сопротивляемости грунта сдвигу, обусловленной в сыпучих телах – внутренним трением, а в связных грунтах – трением и сцеплением.

Видео:Сопротивление грунтов сдвигу и характеристики их прочности (угол внутреннего трения; сцепление)Скачать

НАПРЯЖЕННОЕ СОСТОЯНИЕ ГРУНТА

Если к поверхности грунта основания приложить нагрузку p, в нём возникнет напряженное состояние:

Полные напряжения по граням элемента σ’ и σ» можно разложить на нормальные составляющие σ_z и σ_x и касательные (сдвигающие) τ (рис. 2,а).;

Нормальные напряжения сжимают элемент, а касательные «перекашивают» (поворачивают) его. Если представить, что элемент состоит из шаровых зёрен грунта, связанных в точках контакта, то нормальные напряжения сжимают зёрна и усиливают связи между ними, а касательные стремятся вызвать относительный сдвиг зёрен, т.е. разрушить грунт (рис. 2,б).

В том случае, когда касательные усилия превзойдут сопротивление зёрен в точках контакта, произойдет относительный сдвиг частиц (Δx и Δz на рис 2,в). Эти деформации являются необратимыми и свидетельствуют о разрушении грунта в данной точке. Причиной разрушения являются касательные напряжения τ, которые превзошли величину внутреннего сопротивления грунта сдвигу.

Видео:Определение характеристик прочности грунтов методом одноплоскостного срезаСкачать

ВНУТРЕННЕЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ

Внутреннее сопротивление грунта сдвигу происходит в результате действия сил трения между частицами и сцепления между ними:

1. Силы трения. Характеризуют внутреннее сопротивление в идеально сыпучих телах (чистые пески). Трение возникает в точках контакта частиц и зависит от многих факторов, среди которых основными являются:
— минеральный состав грунта;
— величина зёрен грунта;
— форма зёрен (окатанная, пластинчатая, игольчатая);
— состояние поверхности (округлая, угловатая);
— плотность грунта, степень водонасыщенности и др.
Показатель, характеризующий внутреннее трение в грунтах – это угол внутреннего трения (обозначается символом φ , измеряется в градусах).

2. Силы сцепления. Характеризуют сопротивление структурных связей всякому перемещению связываемых ими частиц, независимо от величины внешнего давления. Сцепление (связность) в грунте определяется:
— наличием капиллярного давления в грунте;
— силами молекулярного притяжения между частицами грунта;
— наличием в грунте вяжущих веществ (известь, минеральные смолы, соли).
Показатель, характеризующий сцепление в грунтах – удельное сцепление (обозначается символом c , измеряется в паскалях). Каким образом определить внутреннее сопротивление грунта сдвигу, характеризуемое показателями φ и c?

Видео:Лекция III-2. Сопротивление грунтов сдвигуСкачать

МЕТОД ОПРЕДЕЛЕНИЯ ПРОЧНОСТНЫХ ХАРАКТЕРИСТИК ГРУНТА

Сопротивление грунта сдвигу может быть установлено различными способами, среди которых наиболее простым и распространённым является способ испытания образца на прямой сдвиг (срез). Последовательность испытания:

1. Цилиндрический образец грунта помещается в «срезыватель» 1 так, чтобы одна его половина оставалась неподвижной, а другая могла перемещаться горизонтально под действием прикладываемой к ней горизонтальной сдвигающей нагрузки (рис. 3);

Рис. 3. N – сжимающая сила; T – сдвигающая сила; Площадь поперечного сечения образца — A

2. К образцу прикладывается нормальная к поверхности среза сжимающая нагрузка N;

3. Сдвигающую касательную к поверхности среза нагрузку T прикладывают к срезывателю ступенями до тех пор, пока не произойдёт срез и скольжение одной части грунта по другой;

4. одновременно с приложением нагрузки и во всё время испытания производятся замеры горизонтальных деформаций (смещений) грунта δ (рис. 4);

5. Проводят несколько испытаний на срез (i штук 2 ) при различных значениях вертикальной (сжимающей) нагрузки N. То есть каждой ступени нагрузки σ_i будет соответствовать своё сопротивление сдвигу τ_i.

6. Данные опытов наносят на график, выражающий зависимость между нормальным напряжением σ и касательным напряжением τ. Опыты показывают, что в общем случае зависимость оказывается линейной.

Видео:Определение границы текучести для глинистых грунтов (конус Васильева)Скачать

УСЛОВИЕ ПРОЧНОСТИ ДЛЯ СЫПУЧИХ И СВЯЗНЫХ ГРУНТОВ

1. Для сыпучих грунтов (различного рода пески, крупнообломочные грунты, галечники). Зависимость σ – τ принимается прямой, проходящей через начало координат и наклонной к оси нормальных напряжений σ под углом внутреннего трения φ (рис. 5).

Из графика можно записать следующую зависимость:

Указанная зависимость – условие прочности грунта (закон Кулона) для сыпучих тел: сопротивление сыпучих грунтов сдвигу есть сопротивление трения, прямо пропорциональное нормальному давлению.

2. Для связных грунтов (пылевато-глинистые грунты) прямая σ – τ не проходит через начало координат, а отсекает отрезок c на оси τ, так как в связных грунтах, обладающих сцеплением между частицами, при отсутствии нормального давления (σ = 0) сопротивление грунта сдвигу больше нуля, что обусловливается силами сцепления (рис. 6).

Общее сопротивление сдвигу связного грунта можно выразить уравнением:

Таким образом, сопротивление связного грунта сдвигу складывается из сопротивления трения, пропорционального нормальному давлению, плюс сцепление, не зависящее от давления.

Видео:Лекция VI-3. Давление грунтов на ограждающие конструкцииСкачать

Расчеты грунтов по модели Кулона-Мора

Критерий прочности Мора-Кулона.

В качестве критерия прочности для оползней скольжения (как в скальных так и в дисперсных грунтах) наиболее часто используется зависимость Мора-Кулона:

где τ — прочность на сдвиг; u – поровое давление; σ – эффективное нормальные напряжения; φ’ – эффективный угол внутреннего трения; с – сцепление.

Графическое представление зависимости Мора-Кулона приведено на рис. 1.

Рис. 1. Графическое представление зависимости Мора-Кулона

Условие Мора-кулона может быть использовано как в полных, так и в эффективных напряжениях. В терминах полных напряжений, критерий Мора-кулона приобретает следующую простую форму:

где t — прочность на сдвиг; s – полное нормальные напряжения; j – угол внутреннего трения; с – сцепление.

Необходимыми свойствами грунтов для расчета устойчивости склона на основе критерия прочности Мора-Кулона являются сцепление и угол внутреннего трения. Они не используются в решении, при расчете напряжений и деформаций, но необходимы для расчета зон пластического течения, в которых значения напряжений превысили критические значения и закон Гука не выполняется. Использование критерия прочности Мора-Кулона позволяет сравнить расчетное напряжение при сдвиге с теоретическими предельными значениями напряжений.

Однако, при решении практических задач, перечень необходимых свойств грунтов для оценки устойчивости склонов, существенно расширяется. В зависимости от постановки задачи в полных или эффективных напряжениях, определение прочностных характеристик грунта должно выполняться по недренируемой схеме, или по схеме консолидируемых дренированных испытаний. При оценки устойчивости оползневых склонов (в условиях протекания оползневого процесса) в зоне скольжения должны использоваться остаточные параметры прочности грунтов, при оценке потенциальной оползневой опасности склона (в случае отсутствия оползневого процесса на исследуемом склоне) – должны использоваться пиковые параметры прочности грунтов.

В свою очередь, удельное сцепление грунтов может быть представлено как сумма двух параметров — сс- структурного сцепления и Σw – связанности грунта при заданной влажности.

По Н.Н. Маслову выделяются три типа глинистых грунтов: жёсткие (хрупко-упругие); скрытопластичные (вязкопластичные) и пластичные (вязкотекучие).

К жёстким глинистым грунтам в большинстве случаев относятся грунты до четвертичного возраста. Связанность жестких глинистых грунтов много меньше их структурного сцепления и может быть приравненной к 0, а угол внутреннего трения мало зависит от влажности. Уравнение сопротивления сдвигу для таких грунтов имеет следующий вид:

Прочность на сдвиг скрыто пластичных глинистых грунтов выражается зависимостью:

При этом величины φ_w и S_w сильно зависят от влажности. В случае нарушения структуры скрытопластичных глинистых грунтов зависимость прочности на сдвиг принимает следующий вид:

Прочность на сдвиг идеально пластичных глинистых грунтов выражается зависимостью:

Как следует из приведенной формулы, в таких грунтах угол внутреннего трения и структурное сцепление принимаются равными 0. В случае нарушения структуры пластичных глинистых грунтов сопротивление прочности на сдвиг в них меняется очень слабо по сравнению с ненарушенной структурой.

В настоящее время существует большое количество модификаций классической зависимости Мора-Кулона. Типичным примером является билинейная модель прочности.

На рис. 1 представлен модифицированный билинейный критерий Мора-Кулона. Огибающая кривая прочности определяется двумя значениями σ (угла внутреннего трения) и удельного сцепления, а также нормальным напряжением в плоскости сдвига, при котором наступает состояние текучести.

Рис. 1. Билинейная модель огибающей кривой сдвига.

Согласно данной модели, в том случае, если нормальное напряжение в плоскости сдвига больше заданного значения, в критерии прочности Мора-Кулона используются значения угла внутреннего трения и сцепления Phi2 и С(computed) соответственно. Билинейная модель прочности была первой попыткой учесть нелинейность в критерии Мора-Кулона.

Типичным примером билинейной модели прочности Мора-Кулона является критерий Паттона (Patton FD (1966). Multiple modes of shear failure in rock. Proceedings of 1st Congress of International Society of Rock Mechanics, Lisbon, 1, 509–513.), разработанный для скальных грунтов и учитывающий эффект шероховатости трещин:

Где φ_b – базовый угол внутреннего трения породы, i – угол шероховатости, σ_n – эффективное напряжение, σ_ny — эффективное нормальное напряжение, вызывающее проскальзывание микродефектов шероховатости, с_jed – эквивалентное сцепление (прочность на сдвиг за счет зацепления микродефектов).

Данная разновидность модели прочности Мора-Кулона, в последние годы так же нашла широкое применение при оценке устойчивости различных нестационарных состояний оползневых (потенциально оползнеопасных) склонов, таких как падение Ку при быстрой сработке уровня подземных вод или при по этапном псевдостатическом анализе учета сейсмического воздействия (Дункан и Райт).

Модель Кулона-Мора пожалуй самая распространенная модель используемая в геотехнических расчетах. С момента создания данной функции прошло уже несколько столетий, при этом модель не только не потеряла своей актуальности, но и постоянно используется в создании новых аналитических выражений. В инженерно-строительной практике данная модель внедренна в различные методики. С ее помощью рассчитывают основания и фундаменты по двум предельным состояниям.