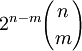Ещё когда я был студентом-первокурсником у меня с одним моим одногруппником вышел горячий спор. Он говорил, что четырёхмерный куб представить нельзя ни в каком виде, а я уверял, что его можно представить достаточно отчётливо. Тогда я даже сделал из скрепок проекцию гиперкуба на наше трёхмерное пространство… Но давайте обо всём по-порядку.
- Что такое гиперкуб и четырёхмерное пространство
- Можно ли представить четырёхмерное пространство и гиперкуб?
- Построение гиперкуба
- 0-мерный куб
- 1-мерный куб
- 2-мерный куб
- 3-мерный куб
- 4-мерный куб (гиперкуб)
- Количество вершин, рёбер, граней
- Проекции и зрение жителя четырёхмерного пространства
- Несколько слов о зрении
- Пересечения рёбер
- Длины рёбер
- Гиперкуб внутри пустой
- Развёртки
- Развёртка трёхмерного куба
- Развёртка четырёхмерного куба
- Пространство-время и евклидово четырёхмерное пространство
- Гиперкуб
- Элементы гиперкуба
- Проекция на плоскость
- Развертка гиперкуба
- Гиперкуб в искусстве
- Заключение
- Что такое тессеракт? Четырехмерный объект, который невозможно построить
- Тессеракт очень трудно визуализировать
- Давайте попробуем визуализировать тессеракт
- Тессеракт был открыт в 1888 году
- Последние исследования
- Пространственные представления человека не ограничены трехмерным миром
- Общее число возможных измерений во Вселенной
- Эксперимент по изучению теоретических материалов в четырехмерном пространстве
- 📸 Видео
Видео:Математика это не ИсламСкачать

Что такое гиперкуб и четырёхмерное пространство
В нашем привычном пространстве три измерения. С геометрической точки зрения это значит, что в нём можно указать три взаимно-перпендикулярных прямых. То есть для любой прямой можно найти вторую, перпендикулярную первой, а для пары можно найти третью прямую, перпендикулярную двум первым. Найти четвёртую прямую, перпендикулярную трём имеющимся, уже не удастся.
Четырёхмерное пространство отличается от нашего только тем, что в нём есть ещё одно дополнительное направление. Если у вас уже есть три взаимно перпендикулярные прямые, то вы можете найти четвёртую, такую, что она будет перпендикуляра всем трём.
Гиперкуб это просто куб в четырёхмерном пространстве.
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Можно ли представить четырёхмерное пространство и гиперкуб?
Этот вопрос сродни вопросу: «можно ли представить Тайную Вечерю, посмотрев на одноимённую картину (1495-1498) Леонардо да Винчи (1452-1519)?»
С одной стороны, вы конечно не представите то, что видел Иисус (он сидит лицом к зрителю), тем более вы не почувствуете запаха сада за окном и вкуса еды на столе, не услышите пения птиц… Вы не получите полного представления о происходившем в тот вечер, но нельзя сказать, что вы не узнаете ничего нового и что картина не представляет никакого интереса.
Аналогичная ситуация и с вопросом о гиперкубе. Полностью представить его нельзя, но можно приблизиться к пониманию, каков он.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Построение гиперкуба
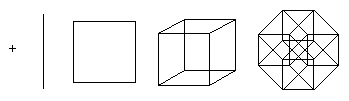
0-мерный куб
Начнём с начала — с 0-мерного куба. Этот куб содержит 0 взаимно перпендикулярных граней, то есть это просто точка.
1-мерный куб
В одномерном пространстве у нас есть только одно направление. Сдвигаем точку в этом направление и получаем отрезок.
Это одномерный куб.
2-мерный куб
У нас появляется второе измерение, сдвигаем наш одномерный куб (отрезок) в направлении второго измерения и получаем квадрат.
Это куб в двумерном пространстве.
3-мерный куб
С появлением третьего измерения поступаем аналогично: сдвигаем квадрат и получаем обычный трёхмерный куб.
4-мерный куб (гиперкуб)
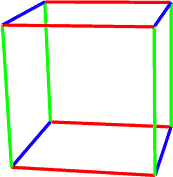
Теперь у нас появилось четвёртое измерение. То есть в нашем распоряжении имеется направление, перпендикулярное всем трём предыдущим. Воспользуемся им точно так же. Четырёхмерный куб будет выглядеть вот так.
Естественно, трёхмерный и четырёхмерный кубы нельзя изобразить на двумерной плоскости экрана. То, что нарисовал я — это проекции. О проекциях мы поговорим чуть позже, а пока немного голых фактов и цифр.
Видео:А.7.19 Поворот в трехмерном пространствеСкачать

Количество вершин, рёбер, граней
| Характеристики кубов различной размерности | |||
|---|---|---|---|
| размерность пространства | количество вершин | количество рёбер | количество граней |
| 0 (точка) | 1 | 0 | 0 |
| 1 (отрезок) | 2 | 1 | 2 (точки) |
| 2 (квадрат) | 4 | 4 | 4 (отрезки) |
| 3 (куб) | 8 | 12 | 6 (квадраты) |
| 4 (гиперкуб) | 16 | 32 | 8 (кубы) |
| N (общая формула) | 2 N | N·2 N-1 | 2·N |
Обратите внимание, что гранью гиперкуба является наш обычный трёхмерный куб. Если внимательно посмотреть на рисунок гиперкуба, то можно действительно найти восемь кубов.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Проекции и зрение жителя четырёхмерного пространства
Несколько слов о зрении
Мы живём в трёхмерном мире, но видим мы его двумерным. Это связано с тем, что сетчатка наших глаз расположена в плоскости, имеющей только два измерения. Именно поэтому мы способны воспринимать двумерные картины и находить их похожими на реальность. (Конечно, благодаря аккомодации, глаз может оценить расстояние до объекта, но это уже побочное явление, связанное с оптикой, встроенной в наш глаз.)
Глаза жителя четырёхмерного пространства должны иметь трёхмерную сетчатку. Такое существо может сразу увидеть трёхмерную фигуру полностью: все её грани и внутренности. (Точно так же мы можем увидеть двумерную фигуру, все её грани и внутренности.)
Таким образом, с помощью наших органов зрения, мы не способны воспринять четырёхмерный куб так, как его воспринимал бы житель четырёхмерного пространства. Увы. Остаётся только уповать на мысленный взор и фантазию, которые, к счастью, не имеют физических ограничений.
Тем не менее, изображая гиперкуб на плоскости, я просто вынужден делать его проекцию на двумерное пространство. Учитывайте это обстоятельство, при изучении рисунков.
Пересечения рёбер
Естественно, ребра гиперкуба не пересекаются. Пересечения появляются только на рисунках. Впрочем, это не должно вызывать удивления, ведь рёбра обычного куба на рисунках тоже пересекаются.
Длины рёбер
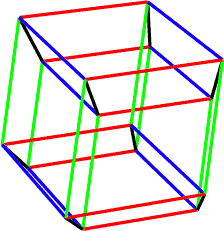
Стоит отметить, что все грани и рёбра четырёхмерного куба равны. На рисунке они получаются не равными только потому, что расположены под разными углами к направлению взгляда. Однако можно развернуть гиперкуб так, что все проекции будут иметь одинаковую длину.
Кстати, на этом рисунке отчётливо видны восемь кубов, являющихся гранями гиперкуба.
Видео:Самый простой способ решить кубическое уравнениеСкачать

Гиперкуб внутри пустой
В это трудно поверить, но между кубами, ограничивающими гиперкуб, заключено некоторое пространство (фрагмент четырёхмерного пространства).
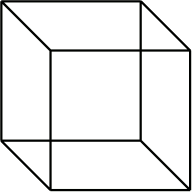
Чтобы это лучше понять, давайте рассмотрим двумерную проекцию обычного трёхмерного куба (я специально сделал её несколько схематичной).
Можно ли по ней догадаться, что внутри куба есть некоторое пространство? Да, но только применив воображение. Глаз этого пространства не видит. Это происходит потому, что рёбра, расположенные в третьем измерении (которое нельзя изобразить на плоском рисунке), теперь превратились в отрезки, лежащие в плоскости рисунка. Они больше не обеспечивают объём.
Квадраты, ограничивающие пространство куба, наложились друг на друга. Но можно представить, что в исходной фигуре (трёхмерном кубе) эти квадраты располагались в разных плоскостях, а не один поверх другого в одной плоскости, как это получилось на рисунке.
Точно так же дело обстоит и с гиперкубом. Кубы-грани гиперкуба на самом деле не накладываются, как это кажется нам на проекции, а располагаются в четырёхмерном пространстве.
Видео:#211. ГИПЕРКУБ и четвертое измерениеСкачать

Развёртки
Итак, житель четырёхмерного пространства может увидеть трёхмерный объект одновременно со всех сторон. Можем ли мы одновременно со всех сторон увидеть трёхмерный куб? Глазом — нет. Но люди придумали способ, как изобразить на плоском рисунке все грани трёхмерного куба одновременно. Такое изображение называется развёрткой.
Развёртка трёхмерного куба
Как образуется развёртка трёхмерного куба все наверно знают. Этот процесс показан на анимации.
Для наглядности края граней куба сделаны полупрозрачными.
Следует отметить, что мы способны воспринять эту двумерную картинку только благодаря воображению. Если рассмотреть фазы разворачивания с чисто двумерной точки зрения, то процесс будет казаться странным и совсем не наглядным.
Он выглядит, как постепенное появление сперва очертаний искажённых квадратов, а потом их расползание на свои места с одновременным принятием необходимой формы.
Если смотреть на разворачивающийся куб в направлении одной из его граней (с этой точки зрения куб выглядит как квадрат), то процесс образования развёртки ещё менее нагляден. Всё выглядит как выползание квадратов из начального квадрата (не развёрнутого куба).
Но не наглядна развёртка только для глаз. Как раз благодаря воображению из неё можно почерпнуть много информации.
Развёртка четырёхмерного куба
Сделать анимированный процесс разворачивания гиперкуба хоть сколько нибудь наглядным просто невозможно. Но этот процесс можно представить. (Для этого надо посмотреть на него глазами четырёхмерного существа.)
Развёртка выглядит так.
Здесь видны все восемь кубов, ограничивающих гиперкуб.
Одинаковыми цветами покрашены грани, которые должны совместиться при сворачивании. Серыми оставлены грани для которых парных не видно. После свёртки самая верхняя грань верхнего куба должна совместиться с нижней гранью нижнего куба. (Аналогично сворачивается развёртка трёхмерного куба.)
Обратите внимание, что после свёртки все грани восьми кубиков придут в соприкосновение, замкнув гиперкуб. И наконец, представляя процесс свёртывания, не забывайте, что при свёртывании происходит не наложение кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области.
Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты фигурируют в очень многих его картинах. На картине «Распятие» (1954) используется развёртка гиперкуба.
Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Пространство-время и евклидово четырёхмерное пространство
Надеюсь, что вам удалось представить гиперкуб. Но удалось ли вам приблизиться к пониманию, как устроено четырёхмерное пространство-время в котором мы живём? Увы, не совсем.
Здесь мы говорили об евклидовом четырёхмерном пространстве, но пространство-время обладает совсем другими свойствами. В частности, при любых поворотах отрезки остаются всегда наклонены к оси времени либо под углом меньше 45 градусов, либо под углом больше 45 градусов.
Свойствам пространства времени я посвятил серию заметок.
Видео:Кубическое уравнение. #ShortsСкачать

Гиперкуб
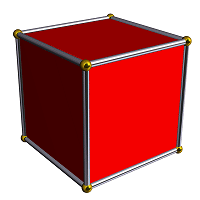 Проекция куба на плоскость |
В геометрии гиперкуб — это n-мерная аналогия квадрата (n = 2) и куба (n = 3). Это замкнутая выпуклая фигура, состоящая из групп параллельных линий, расположенных на противоположных краях фигуры, и соединенных друг с другом под прямым углом.
Эта фигура также известная под названием тессеракт (tesseract). Тессеракт относится к кубу, как куб относится к квадрату. Более формально, тессеракт может быть описан как правильный выпуклый четырехмерный политоп (многогранник), чья граница состоит из восьми кубических ячеек.
Согласно Окфордскому словарю английского языка, слово «tesseract» было придумано в 1888 Чарльзом Говардом Хинтоном (Charles Howard Hinton) и использовано в его книге «Новая эра мысли» («A New Era of Thought»). Слово было образовано от греческого «τεσσερες ακτινες» («четыре луча»), имеется в виде четыре оси координат. Кроме этого, в некоторых источниках, эту же фигуру называли тетракубом (tetracube).
n-мерный гиперкуб также называется n-кубом.
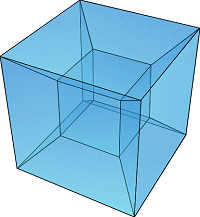 Проекция гиперкуба на плоскость |
Точка — это гиперкуб размерности 0. Если сдвинуть точку на единицу длины, получится отрезок единичной длины — гиперкуб размерности 1. Далее, если сдвинуть отрезок на единицу длины в направлении перпендикулярном направлению отрезка получится куб — гиперкуб размерности 2. Сдвигая квадрат на единицу длины в направлении перпендикулярном плоскости квадрата, получается куб — гиперкуб размерности 3. Этот процесс может быть обобщен на любое количество измерений. Например, если сдвинуть куб на единицу длины в четвертом измерении, получится тессеракт.
Семейство гиперкубов является одним из немногих правильных многогранников, которые могут быть представлены в любом измерении.
Видео:Решение кубических уравненийСкачать

Элементы гиперкуба
Гиперкуб размерности n имеет 2n «сторон» (одномерная линия имеет 2 точки; двухмерный квадрат — 4 стороны; трехмерный куб — 6 граней; четырехмерный тессеракт — 8 ячеек). Количество вершин (точек) гиперкуба равно 2 n (например, для куба — 2 3 вершин).
Количество m-мерных гиперкубов на границе n-куба равно
Например, на границе гиперкуба находятся 8 кубов, 24 квадрата, 32 ребра и 16 вершин.
| n-куб | Название | Вершина (0-грань) | Ребро (1-грань) | Грань (2-грань) | Ячейка (3-грань) | (4-грань) | (5-грань) | (6-грань) | (7-грань) | (8-грань) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-куб | Точка | 1 | ||||||||
| 1-куб | Отрезок | 2 | 1 | |||||||
| 2-куб | Квадрат | 4 | 4 | 1 | ||||||
| 3-куб | Куб | 8 | 12 | 6 | 1 | |||||
| 4-куб | Тессеракт | 16 | 32 | 24 | 8 | 1 | ||||
| 5-куб | Пентеракт | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-куб | Хексеракт | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-куб | Хептеракт | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-куб | Октеракт | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-куб | Эненеракт | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Видео:ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Проекция на плоскость
Формирование гиперкуба может быть представлено следующим способом:
- Две точки A и B могут быть соединены, образуя отрезок AB.
- Два параллельных отрезка AB и CD могут быть соединены, образуя квадрат ABCD.
- Два параллельных квадрата ABCD и EFGH могут быть соединены, образуя куб ABCDEFGH.
- Два параллельных куба ABCDEFGH и IJKLMNOP могут быть соединены, образуя гиперкуб ABCDEFGHIJKLMNOP.
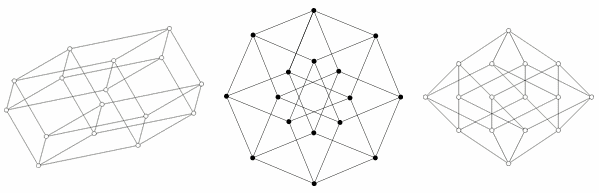
Последнюю структуру нелегко представить, но возможно изобразить ее проекцию на двухмерное или трехмерное пространство. Более того, проекции на двухмерную плоскость могут быть более полезны возможностью перестановки позиций спроецированных вершин. В этом случае можно получить изображения, которые больше не отражают пространственные отношения элементов внутри тессеракта, но иллюстрируют структуру соединений вершин, как на примерах ниже.
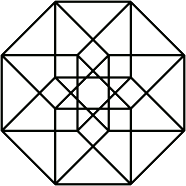
На первой иллюстрации показано, как в принципе образуется тессеракт путем соединения двух кубов. Эта схема похожа на схему создания куба из двух квадратов. На второй схеме показано, что все ребра тессеракта имеют одинаковую длину. Эта схема также заставляют искать соединенные друг с другом кубы. На третьей схеме вершины тессеракта расположены в соответствии с расстояниями вдоль граней относительно нижней точки. Эта схема интересна тем, что она используется как базовая схема для сетевой топологии соединения процессоров при организации параллельных вычислений: расстояние между любыми двумя узлами не превышает 4 длин ребер, и существует много различных путей для уравновешивания нагрузки.
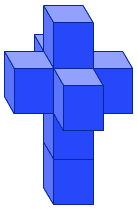 Развертка тессеракта |
Видео:Решение уравнения третьей степени x³-9x-12=0Скачать

Развертка гиперкуба
Тессеракт может быть развернут в восемь кубов, подобно тому как куб может быть развернут в шесть квадратов. Многогранник-равертка гиперкуба называется сетью. Существует 261 различных вариантов сетей. Справа показан один из вариантов
 Сальвадор Дали «Распятие» (1954) |
Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Гиперкуб в искусстве
Гиперкуб появился в научно-фантастической литературе с 1940 года, когда Роберт Хайнлайн в рассказе «Дом, который построил Тил» («And He Built a Crooked House») описал дом, построенный по форме развертки тессеракта. В рассказе этот Далее этот дом сворачивается, превращаясь в четырехмерный тессеракт. После этого гиперкуб появляется во многих книгах и новеллах.
В фильме «Куб 2: Гиперкуб» рассказывается о восьми людях, запертых в сети гиперкубов.
На картине Сальвадора Дали «Распятие» («Crucifixion (Corpus Hypercubus)», 1954) изображен Иисус распятый на развертке тессеракта. Эту картину можно увидеть в Музее Искусств (Metropolitan Museum of Art) в Нью-Йорке.
Видео:Уравнение прямой в пространстве. 11 класс.Скачать

Заключение
Гиперкуб — одна из простейших четырехмерных объектов, на примере которого можно увидеть всю сложность и необычность четвертого измерения. И то, что выглядит невозможным в трех измерениях, возможно в четырех, например, невозможные фигур. Так, например, бруски невозможного треугольника в четырех измерениях будут соединены под прямыми углами. И эта фигура будет выглядеть так со всех точек обзора, и не будет искажаться в отличие от реализаций невозможного треугольника в трехмерном пространстве (см. «Невозможные фигуры в реальном мире»).
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Что такое тессеракт? Четырехмерный объект, который невозможно построить
Тессеракт — это четырехмерный гиперкуб с 24 гранями, 32 ребрами и 16 вершинами. Он может быть создан путем утолщения куба в четвертом измерении. Хотя тессеракт невозможно построить физически, мы можем визуализировать его в нашем трехмерном мире.
Идея четвертого пространственного измерения манила людей с момента ее появления. В физике три измерения представляют собой пространство (x,y,z), а четвертое измерение — время (t). Однако в абстрактной математической концепции может существовать бесконечное число пространственных измерений.
Давайте попробуем понять четвертое измерение. В геометрии четырехмерный аналог куба называется тессерактом. Его легко экстраполировать, рассматривая более низкие измерения.
- Нульмерный куб — это точка, вершина.
- Одномерный куб — это отрезок прямой с 2 вершинами (по одной на каждом конце). Его можно создать путем увеличения толщины точки в одном измерении.
- Двумерный куб — это квадрат с 4 вершинами. Его можно создать, увеличив толщину отрезка линии во втором измерении.
- Трехмерный куб — это куб с 8 вершинами, созданный путем увеличения толщины квадрата в третьем измерении.
Аналогично, четырехмерный куб (также известный как гиперкуб или тессеракт) имеет 16 вершин. Он может быть создан путем сгущения куба в четвертом измерении. Но поскольку мы живем в трехмерном мире, построить четырехмерный объект невозможно.
В целом можно сказать, что тессеракт относится к кубу так же, как куб относится к квадрату. У него 24 грани, 32 ребра и 16 вершин.

Видео:КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Тессеракт очень трудно визуализировать
Визуализировать тессеракт или любой другой четырехмерный объект чрезвычайно трудно, если вообще возможно. Это происходит потому, что наше воображение недостаточно сильно, чтобы спроецировать наше сознание в искусственный мир, который сильно отличается от нашего собственного.
Наш мозг устроен так, чтобы преобразовывать двухмерные данные в трехмерное представление. Точнее, наши глаза посылают в мозг пару двухмерных изображений, из которых мозг строит двухмерную+глубинную модель поля зрения.
Это то, о чем наш мозг лучше всего приспособлен думать. Трехмерное пространство легко визуализировать, потому что мы буквально видим его все время. Однако у нас нет прямого опыта более высоких измерений, и поэтому у людей нет четкого прототипа, который можно было бы использовать в качестве трамплина для их визуализации.
С другой стороны, физики и математики, имеющие опыт работы с более высокоразмерными пространствами, более способны, чем остальные, визуализировать их в своем мозгу.
Давайте попробуем визуализировать тессеракт
Как куб можно спроецировать в двухмерное пространство, так и тессеракт можно спроецировать в трехмерное пространство.
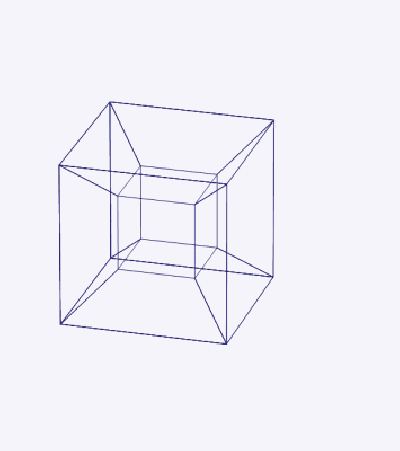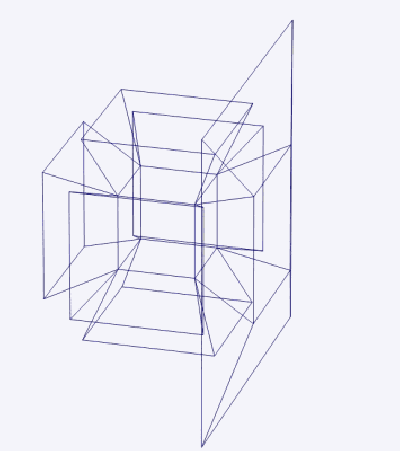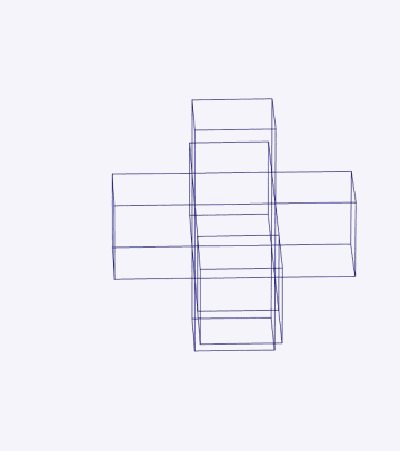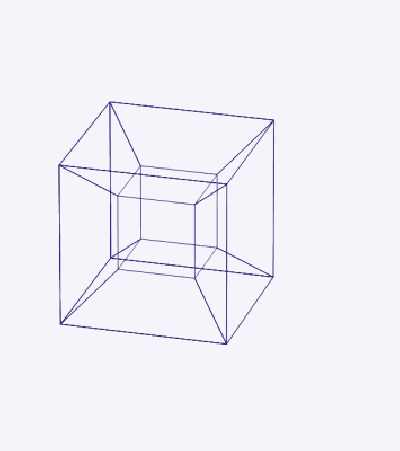
Поверхность трехмерного куба содержит 6 квадратных граней; аналогично гиперповерхность тессеракта содержит 8 кубических ячеек.
Тессеракт можно развернуть на 8 кубиков в трехмерном пространстве (рис. 2). Это похоже на развертывание куба на 6 квадратов в двумерном пространстве. Разворачивание геометрического объекта [с плоскими сторонами] называется сеткой. В тессеракте 261 сетка.
Существует два типа четырехмерных вращений:
1) Простые вращения: трехмерная проекция Тессеракта (рис. 3), выполняющая простое вращение вокруг плоскости, разделяющей пополам фигуру сверху вниз и спереди слева направо.

2) Двойное вращение: трехмерная проекция тессеракта (рис. 4), показывающая двойное вращение вокруг двух ортогональных плоскостей.

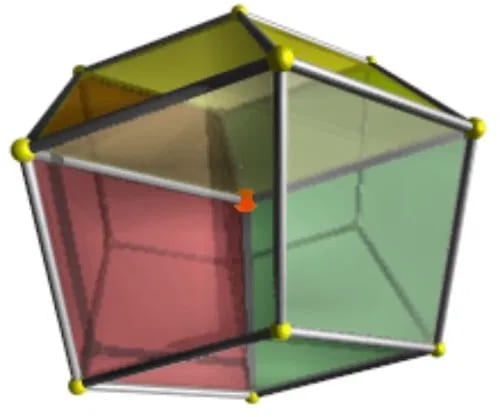
Тессеракт также может быть показан с точки зрения устранения скрытого объема. На рисунке 5, например, красная грань находится ближе всего к четвертому измерению и имеет четыре кубические ячейки, расположенные вокруг нее.
Рисунок 5 | Тессеракт с точки зрения устранения скрытого объема
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Тессеракт был открыт в 1888 году
Слово «тессеракт» было придумано британским математиком и писателем-фантастом Чарльзом Говардом Хинтоном. Он впервые использовал это слово в 1888 году в своей книге «Новая эра мышления». Он также придумал несколько новых слов для описания элементов в четвертом измерении.
С тех пор слово «тессеракт» используется в различных видах искусства, архитектуры и научно-фантастических историях (таких, как «Мстители» и «Агенты «Щ.И.Т.»»), где оно не имеет ничего общего с четырехмерным гиперкубом.
Видео:ВМ. ШМ. 7.2 Угол между двумя плоскостями. Координаты вершин куба.Скачать

Последние исследования
Пространственные представления человека не ограничены трехмерным миром
Группа исследователей из Университета Иллинойса, США, провела исследование, чтобы выяснить, может ли человек развить интуитивное понимание четырехмерного пространства. Для получения точных результатов они использовали виртуальную реальность (VR).
Данные показывают, что люди, не имеющие специальной практики, могут научиться делать пространственные суждения о длине и угле между линейными сегментами, встроенными в четырехмерное пространство, просматриваемое в виртуальной реальности. Их суждение включало данные как трехмерной проекции, так и четвертого измерения. Основные представления были основаны на визуальных образах (установленных алгебраической природы), хотя и примитивных и недолговечных.
Общее число возможных измерений во Вселенной
В то время как общая теория относительности рисует картину четырехмерной Вселенной, теория суперструн утверждает, что она имеет 10 измерений, а расширенная версия, называемая М-теорией, утверждает, что она имеет 11 измерений. В бозонической теории струн пространственное время 26-мерно. Эти теории просто представляют собой математические уравнения. Они настолько сложны, что никто не знает их точной формы.
Эксперимент по изучению теоретических материалов в четырехмерном пространстве
Международная группа исследователей смогла разработать двумерную экспериментальную систему, которая позволяет им анализировать физические свойства «материалов», которые теоретически существуют только в четырехмерном пространстве.
Более конкретно, они продемонстрировали, что четырехмерные квантовые эффекты Холла могут быть эмулированы с помощью фотонов, проходящих через двумерный волноводный массив.
Как эти исследования могут быть полезны в нашем трехмерном мире? Скажем, квазикристаллы (широко используемые для покрытия некоторых антипригарных сковородок), как было показано, имеют скрытые измерения. Этот эксперимент может помочь нам понять физику этого скрытого измерения. Затем эта физика может быть использована в качестве принципа проектирования нового фотонного оборудования.
📸 Видео
Уравнение плоскости. 11 класс.Скачать

Подстановка Виета или как решить кубическое уравнение, представив его в виде куба разности.Скачать