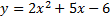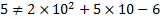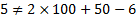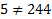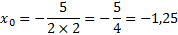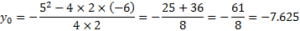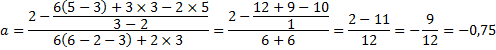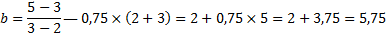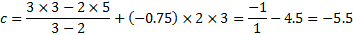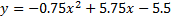Уравнение кривой по трем точкам (6 видео)

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

дано уравнение и надо построить фигуру Ф, уравнением которой является ;
дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
Записать в координатах условие, сформулированное в первом пункте.

Содержание

Эллипс
Гипербола
Кривые второго порядка на плоскости
Уравнения кривых.
Уравнение по трем точкам: как найти вершину параболы, формула
Начало поиска
Расчет коэффициентов и основных точек параболы
Численное значение координаты вершины на оси абсцисс
Значение вершины на оси ординат
Построение кривой параболического типа
Наглядные примеры
Вывод
📺 Видео

Видео:Видеоурок "Уравнение плоскости по трем точкам"Скачать

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнения кривых.

В аналитической геометрии всякому уравнению вида F(x; у) = 0 может соответствовать некоторая линия, свойства которой определяются данным уравнением.

Под F(x; у) = 0 понимаем многочлен степени n; степень многочлена n – порядок линии.

Значит, кривая первого порядка, в декартовой системе координат, описывается алгебраическим уравнением первого порядка ax + by + c = 0, где хотя бы один из коэффициентов a или b отличен от нуля. Это уравнение называют также линейным уравнением. А само выражение, типа ax+by+c=0 и a 2 +b 2 ≠ 0, принято обозначать как общее уравнение прямой.

Следовательно, любая прямая на плоскости представляет собой алгебраическую кривую первого порядка и любая алгебраическая кривая первого порядка на плоскости есть прямая.

Общее уравнение кривой второго порядка в декартовых координатах имеет вид:

причем, в зависимости от значения произведение аb получаем:

— эллипс, частный случай — окружность ( когда ab > 0);

Видео:11. Прямая в пространстве и ее уравненияСкачать

Уравнение по трем точкам: как найти вершину параболы, формула

Многие технические, экономические и социальные вопросы прогнозируются при помощи кривых. Наиболее используемым типом среди них является парабола, а точнее, ее половина. Важной составляющей любой параболической кривой является ее вершина, определение точных координат которой иногда играет ключевую роль не только в самом отображении протекания процесса, но и для последующих выводов. О том, как найти ее точные координаты, и пойдет речь в данной статье….

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Начало поиска

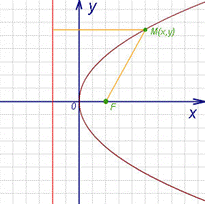
Перед тем как перейти к поиску координат вершины параболы, ознакомимся с самим определением и его свойствами. В классическом понимании параболой называется такое расположение точек, которые удалены на одинаковом расстоянии от конкретной точки (фокус, точка F), а также от прямой, которая не проходит через точку F. Рассмотрим данное определение более предметно на рисунке 1.

Рисунок 1. Классический вид параболы

На рисунке изображена классическая форма. Фокусом является точка F. Директрисой в данном случае будет считаться прямая параллельная оси Y (выделена красным цветом). Из определения можно удостовериться, что абсолютно любая точка кривой, не считая фокуса, имеет себе подобную с другой стороны, удаленную на таком же расстояние от оси симметрии, как и сама. Более того, расстояние от любой из точек на параболе равно расстоянию до директрисы. Забегая вперед, скажем, что центр функции не обязательно должен находиться в начале координат, а ветки могут быть направлены в разные стороны.

Парабола, как и любая другая функция, имеет свою запись в виде формулы:

(1).

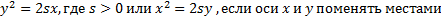
В указанной формуле буква «s» обозначает параметр параболы, которая равна расстоянию от фокуса до директрисы. Также есть и другая форма записи, указано ГМТ, имеющая вид:

(2).

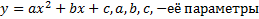
Такая формула используется при решении задач из области математического анализа и применяется чаще, чем традиционная (в силу удобства). В дальнейшем будем ориентироваться на вторую запись.

Это интересно! Первый признак равенства треугольников: доказательство

Видео:Репетитор по математике пишет уравнение плоскости по трем точкамСкачать

Расчет коэффициентов и основных точек параболы

К числу основных параметров принято относить расположение вершины на оси абсцисс, координаты вершины на оси ординат, параметр директрисы.

Численное значение координаты вершины на оси абсцисс

Если уравнение параболы задано в классическом виде (1), то значение абсциссы в искомой точке будет равняться половине значения параметра s (половине расстояния между директрисой и фокусом). В случае, если функция представлена в виде (2), то x нулевое рассчитывается по формуле:

(3).

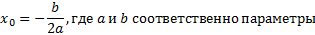
Т.е., глядя на эту формулу, можно утверждать, что вершина будет находиться в правой половине относительно оси y в том случае, если один из параметров a или b будет меньше нуля.

Уравнение директрисы определяется следующим уравнением:

(4).

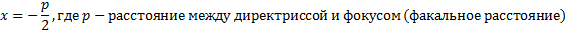
Это интересно! Что такое деление с остатком: примеры для ребенка в 3, 4 классе

Значение вершины на оси ординат

Численное значение местонахождения вершины для формулы (2) на оси ординат можно найти по такой формуле:

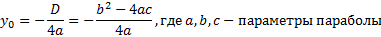
Отсюда можно сделать вывод, что в случае если а&lt,0, то вершина кривой будет находиться в верхней полуплоскости, в противном случае – в нижней. При этом точки параболы будут обладать теми же свойствами, что были упомянуты ранее.

Если дана классическая форма записи, то более рациональным будет вычисление значения расположения вершины на оси абсцисс, а через него и последующее значение ординаты. Отметим, что для формы записи (2), ось симметрии параболы, в классическом представлении, будет совпадать с осью ординат.

Важно! При решении заданий с использованием уравнения параболы прежде всего выделите основные значения, которые уже известны. Более того, нелишним будет, если будут определены недостающие параметры. Такой подход заранее даст большее «пространство для маневра» и более рациональное решение. На практике старайтесь использовать запись (2). Она более проста для восприятия (не придется «переворачивать координаты Декарта), к тому же подавляющее количество заданий приспособлено именно под такую форму записи.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Видео:Уравнение плоскости через 3 точкиСкачать

Построение кривой параболического типа

Используя распространенную форму записи, перед тем как построить параболу, требуется найти ее вершину. Проще говоря, необходимо выполнить следующий алгоритм:

Найти координату вершину на оси X.
Найти координату расположения вершины на оси Y.
Подставляя разные значения зависимой переменной X, найти соответствующие значения Y и построить кривую.

Т.е. алгоритм не представляет собой ничего сложного, основной акцент делается на том, как найти вершину параболы. Дальнейший процесс построения можно считать механическим.

При условии, что даны три точки, координаты которых известны, прежде всего необходимо составить уравнение самой параболы, а потом повторить порядок действий, который был описан ранее. Т.к. в уравнении (2) присутствуют 3 коэффициента, то, используя координаты точек, вычислим каждое из них:

(5.1).

(5.2).

(5.3).

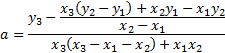
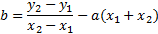
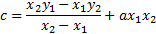
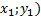
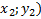
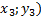
В формулах (5.1), (5.2), (5.3) применяются соответственно тех точек, которые известны (к примеру А ( , B (, C ( . Таким путем находим уравнение параболы по 3 точкам. С практической стороны такой подход не является самым «приятным», однако он дает четкий результат, на основе которого впоследствии строится сама кривая.

При построении параболы всегда должна присутствовать ось симметрии. Формула оси симметрии для записи (2) будет иметь такой вид:

(6).

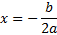
Т.е. найти ось симметрии, которой симметричны все точки кривой, не составляет труда. Точнее, она равна первой координате вершины.

Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Наглядные примеры

Пример 1. Допустим, имеем уравнение параболы:

Требуется найти координаты вершины параболы, а также проверить, принадлежит ли точка D (10, 5) данной кривой.

Решение: Прежде всего проверим принадлежность упомянутой точки самой кривой

Откуда делаем вывод, что указанная точка не принадлежит заданной кривой. Найдем координаты вершины параболы. Из формул (4) и (5) получаем такую последовательность:

Получается, что координаты на вершине, в точке О, следующие (-1,25, -7,625). Это говорит о том, что наша парабола берет свое начало в 3-й четверти декартовой системы координат.

Пример 2. Найти вершину параболы, зная три точки, которые ей принадлежат: A (2,3), B (3,5), C (6,2). Используя формулы (5.1), (5.2), (5.3), найдем коэффициенты уравнения параболы. Получим следующее:

Используя полученные значения, получим следующие уравнение:

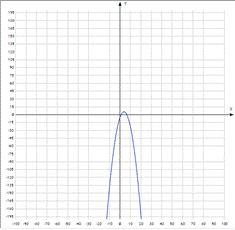
На рисунке заданная функция будет выглядеть следующим образом (рисунок 2):

Рисунок 2. График параболы, проходящий через 3 точки

Т.е. график параболы, который проходит по трем заданным точкам, будет иметь вершину в 1-й четверти. Однако ветки данной кривой направлены вниз, т.е. имеется смещение параболы от начала координат. Такое построение можно было предвидеть, обратив внимание на коэффициенты a, b, c.

В частности, если a&lt,0, то ветки» будут направлены вниз. При a&gt,1 кривая будет растянута, а если меньше 1 – сжата.

Константа c отвечает за «движение» кривой вдоль оси ординат. Если c&gt,0, то парабола «ползет» вверх, в противном случае – вниз. Относительно коэффициента b, то определить степень влияния можно лишь изменив форму записи уравнения, приведя ее к следующему виду:

Если коэффициент b&gt,0, то координаты вершины параболы будут смещены вправо на b единиц, если меньше – то на b единиц влево.

Важно! Использование приемов определения смещения параболы на координатной плоскости подчас помогает экономить время при решении задач либо узнать о возможном пересечении параболы с другой кривой еще до построения. Обычно смотрят только на коэффициент a, так как именно он дает четкий ответ на поставленный вопрос.

Полезное видео: как найти вершину параболы

Полезное видео: как легко составить уравнение параболы из графика

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Вывод

Такой как алгебраический процесс, как определение вершин параболы, не является сложным, но при этом достаточно трудоемкий. На практике стараются использовать именно вторую форму записи с целью облегчения понимания графического решения и решения в целом. Поэтому настоятельно рекомендуем использовать именно такой подход, и если не помнить формулы координаты вершины, то хотя бы иметь шпаргалку.