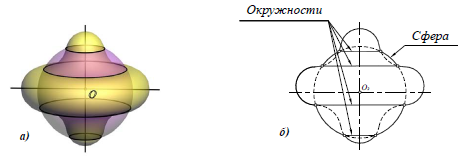(лекции №3, 4, 5,практические занятия №2, 3, контр. работа 20 мин.)
1)Понятие кривой в пространстве. Параметрическое задание кривой.
2)Уравнения касательной в случае параметрического задания кривой и в случае задания кривой, как пересечения двух поверхностей.
3)Длина дуги кривой. Натуральный параметр кривой.
4)Определение 2.1 (Круг, радиус и центр кривизны, кривизна)
5)Определение 2.2 (главная нормаль и формула для её нахождения).
6)Определение 2.3 (бинормаль и формула для её нахождения).
7)Определение 2.4 (плоскостей сопровождающего трёхгранника).
8)Формулы Френе. Кручение.
9)Определение 2.5 (эволюты). Уравнение эволюты.
10)Определение 2.6 (эвольвенты).
2.1 ЗАДАНИЕ ЛИНИИ В ПРОСТРАНСТВЕ.
Под кривой в пространстве будем понимать множествоГточек в пространстве, заданное, как непрерывный образ некоторого промежутка числовой оси.
Кривую можно задать параметрически:

или как годограф вектор-функции 

2.2 КАСАТЕЛЬНАЯ КРИВОЙ.
Кривая называется дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д., если соответственно координатные функции в формуле (2.1) дифференцируемы, непрерывно дифференцируемы, дважды дифференцируемы и т.д.
ПустьГ– дифференцируемая кривая, заданная как годограф вектор-функции 






В случае задания кривой уравнениями
x=x,y=f(x),
(здесь роль параметра играет переменнаях), уравнения касательной имеют вид:

Составим уравнение касательной к кривой, заданной, как пересечение двух поверхностей, заданных уравнениями в неявной форме
Дифференцируя эти тождества, получим
Отсюда видно, что вектор касательной 


Если на кривой указать положительное направление, соответствующее возрастанию параметраt,то вектор 
Углом между ориентированными кривыми, пересекающимися в некоторой точке, называется угол между их касательными в этой точке.
Пример 2.1Составить уравнения касательной к винтовой линии: 

Решение. Так как 

В частности при 
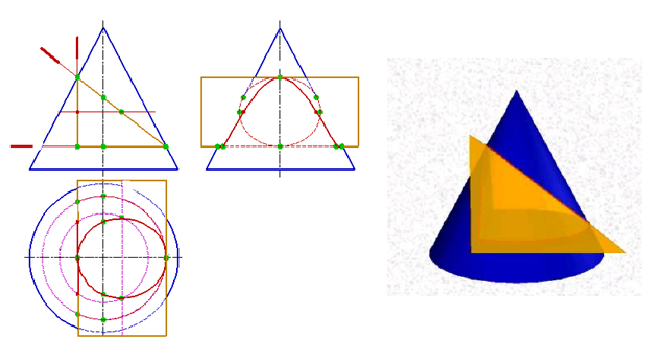
Пример 2.2Составить уравнения касательной к кривой Вивиани:x 2 +y 2 +z 2 =R 2 ,x 2 +y 2 =Rxв точкеМ0(R/2,R/2, 
Решение: Кривая Вивиани является линией пересечения поверхностей сферы с центром в начале координат и кругового цилиндра с центром (образующей), смещенным вдоль оси (в данном случае)Охна величину, равную радиусу цилиндра. Диаметр цилиндра равен радиусу сферы.
Запишем уравнения поверхностей в неявном виде


Тогда 
или 
В точкеМ0(R/2,R/2, 
2.3ДЛИНА КРИВОЙ. НАТУРАЛЬНЫЙ ПАРАМЕТР КИВОЙ.
Рассмотрим дугу непрерывно дифференцируемой кривой
Г: x=x(t), y=y(t), z=z(t), 
В разделе «Определённый интеграл» мы получили формулу для нахождения длины дуги кривой:

Если в качестве параметра выбрана координатах,и криваязадана уравнениями:x=x,y=y(x),z=z(x), 

При переменном верхнем пределе длина дуги будет переменной величиной:


Если параметромtкривой является переменная длина дугиs, то координаты точки М кривой будут зависеть от длины дугиs=АМ:x=x(s),y=y(s),z=z(s)(естественная параметризация).Тогда в формуле (2.7) 


Точка(x(t0),y(t0),z(t0))кривой называется особой, если 

Для всякой непрерывно дифференцируемой кривой без особых точек существует ее представление 
Пример 2.3Найти длину дугиs(t)винтовой линии
x=acost,y=asint,z=bt, 
Решение: Касательный вектор 

Пример 2.4Записать натуральную параметризацию винтовой линии.
Решение: Длина дуги линии 


- Лекция 8. Пересечение кривых поверхностей
- 8.1. Частные случаи
- 8.2. Алгоритм построения точек кривой пересечения двух поверхностей
- 8.3. Задачи для самостоятельной работы
- Взаимное пересечение поверхностей в начертательной геометрии с примерами
- Взаимное пересечение поверхностей
- Пересечение двух многогранников
- Пересечение гранной и кривой поверхности
- Пересечение двух кривых поверхностей. Метод вспомогательных секущих плоскостей
- Пересечение поверхностей вращении. Метод вспомогательных секущих сфер
- Теорема Монжа
- Пересечение поверхностей вращения с многогранниками
- Пересечение поверхностей вращения
- Способ вспомогательных секущих плоскостей
- Пересечение цилиндрической и торовой поверхности
- Особые случаи пересечения
- Пересечение соосных поверхностей вращения
- Теорема Монжа для пересекающихся поверхностей вращения
- Способ вспомогательных секущих сфер
- Способ вспомогательных секущих плоскостей
- Способ вспомогательных сфер
- Элементы технического рисования
- Взаимное пересечение поверхностей с примерами
- Способ вспомогательных параллельных плоскостей
- Способ вспомогательных сфер
- Способ концентрических сфер
- 📽️ Видео
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Лекция 8. Пересечение кривых поверхностей
В общем случае кривые поверхности второго порядка (цилиндр, конус, сфера) пересекаются по пространственной кривой четвертого порядка. Эта лекальная кривая строится по точкам.
В общем случае эти точки находятся как точки пересечения образующих одной поверхности с образующими другой, а потом точки последовательно соединяют линией с учётом видимости.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

8.1. Частные случаи
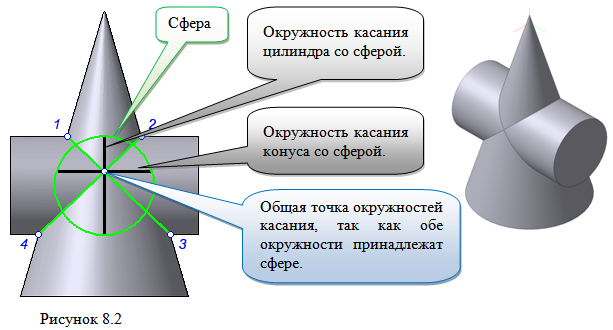
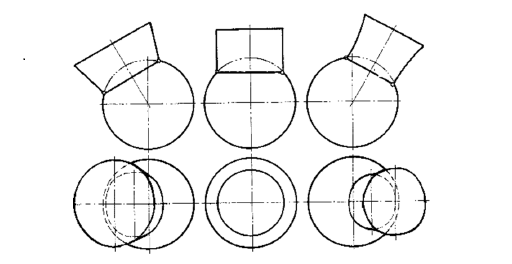
Теорема Монжа 1 . Две поверхности, описанные вокруг общей сферы, пересекаются по двум плоским кривым (Рисунок 8.1).
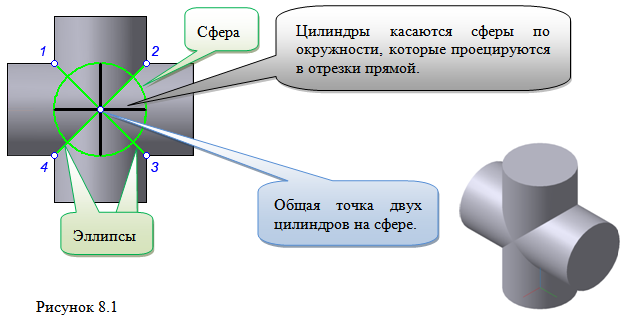
Крайние образующие цилиндров пересекаются в точках 1, 2, 3, 4.
Цилиндры пересекаются по эллипсам.
Крайние образующие пересекаются в точках 1, 2, 3, 4.
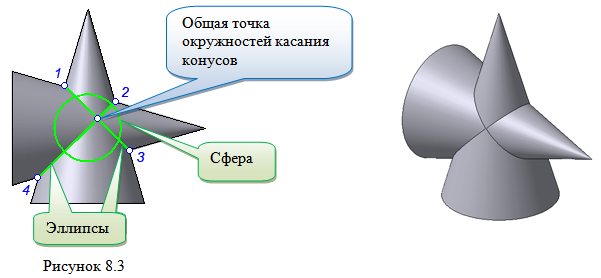
Теорема Монжа 2 . Если две пересекающиеся поверхности второго порядка имеют общую плоскость симметрии, параллельную некоторой плоскости проекций, то на эту плоскость проекций линия их пересечения проецируется в кривую второго порядка. Если это условие не выполнено, то – в кривую четвертого порядка. Эту плоскость называют плоскостью параллелизма .
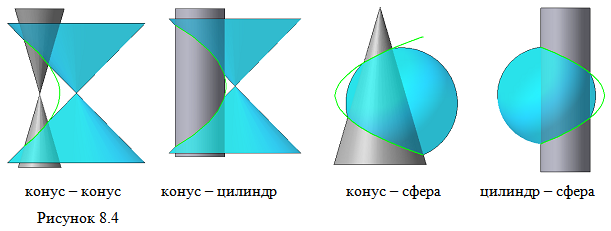
Рассмотрим четыре примера пересечения тел вращения, у которых оси вращения лежат в одной плоскости, параллельной плоскости проекций π2 (Рисунок 8.4). Следовательно, данная плоскость является плоскостью симметрии пересекающихся тел, параллельная плоскости проекций π2. Это означает, что линия пересечений тел проецируется на плоскость проекций π2 как кривая второго порядка – парабола.
Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

8.2. Алгоритм построения точек кривой пересечения двух поверхностей
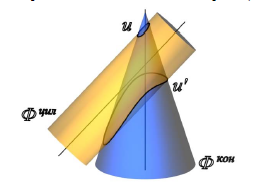
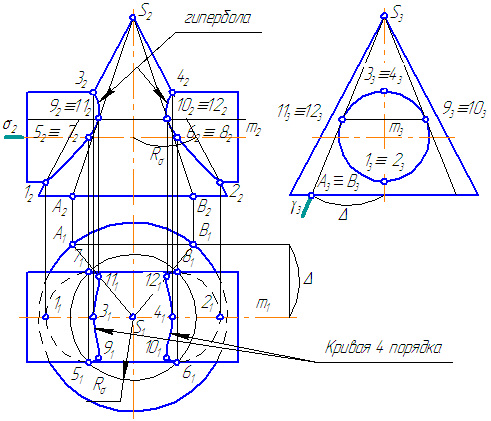
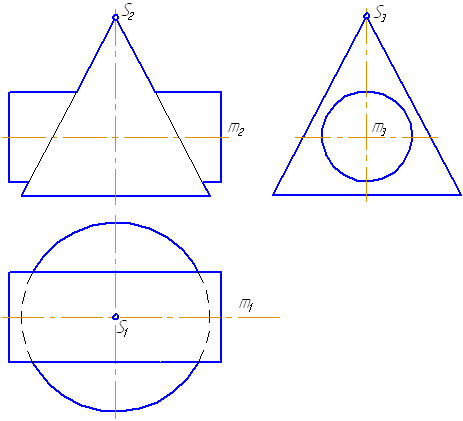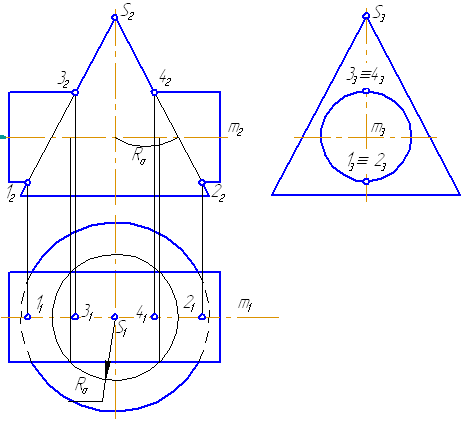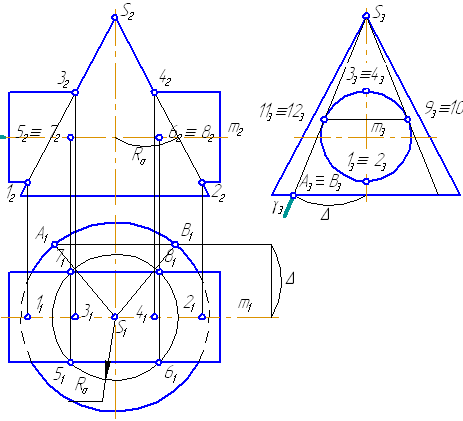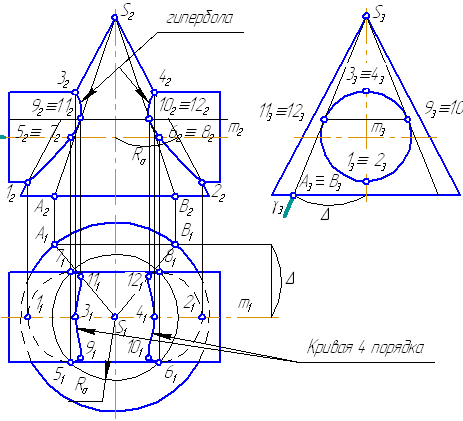
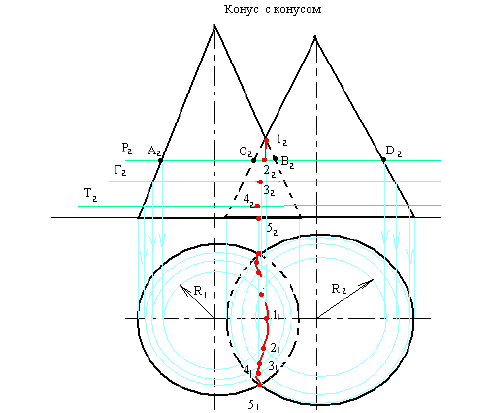
- Выполним анализ кривых пересечения цилиндра и конуса (Рисунок 8.5): у данных тел есть общая плоскость симметрии, параллельная плоскости проекций π2, следовательно, (согласно второй теореме Монжа) на π2 кривые пересечения тел 4-го порядка проецируются в виде кривых второго порядка. Поскольку при этом получается две ветви, следовательно, это будет гипербола.
- Строим характерные точки: пересечение крайних образующих на π2 цилиндра и конуса, точки 1, 2, 3, 4.
- Для нахождения точек, лежащих на крайних образующих на π1 цилиндра, введём плоскость σ⊥π2 и σ//π1 проходящую через фронтальную проекцию оси вращения цилиндра. В результате данная плоскость пересечет цилиндр по крайним образующим, а конус – по окружности радиусом Rσ. Построенные на π1 сечения пересекутся в точках 5, 6, 7, 8. По линии проекционной связи строим их фронтальные проекции.
- Для построения самых близких друг к другу точек кривой на π2 введём плоскость γ⊥π3, проходящую через вершину конуса и касательную к цилиндру. Данная плоскость пересечёт конус по треугольнику SAB. Построив образующие конуса SA, SB и цилиндра 11-12, на их пересечении определим точки 11, 12. Точки 9, 10 построим симметрично точкам 11 и 12.
- Для построения дополнительных промежуточных точек, можно ввести вспомогательные секущие плоскости (посредники) параллельно σ.
Рисунок 8.5 – Построение линии пересечения конуса и цилиндра
На анимации ниже представлена последовательность построения линии пересечения конуса и цилиндра.
Рисунок 8.6 – Последовательность построения линии пересечения конуса и цилиндра
Видео:Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

8.3. Задачи для самостоятельной работы
1-2. Построить линию пересечения поверхностей вращения (Рисунки 8.7, 8.8).
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Взаимное пересечение поверхностей в начертательной геометрии с примерами
Содержание:
Взаимное пересечение поверхностей:
При пересечении поверхностей образуется линия, которую принято называть линией взаимного пересечения поверхностей. Эта линия пересечения принадлежит одновременно двум поверхностям. Поэтому построение линии пересечения сводится к определению точек одновременно принадлежащих обеим поверхностям. Для нахождения таких точек используется в общем случае метод вспомогательных секущих поверхностей. Сущность способа заключается в следующем: Пусть задано две поверхности
Общий алгоритм построения линии пересечения поверхностей:
- Введем вспомогательную поверхность Ф.
- Строим линии пересечения поверхности Ф с поверхностями
- Определяем точки пересечения К и М, простроенных линий a и b
- Многократно повторяя эту операцию, найдем ряд точек, принадлежащих одновременно двум поверхностям.
- Соединяем последовательно точки с учетом видимости.
В качестве посредников могут быть приняты как поверхности, так и плоскости, но целесообразно выбирать такие, которые дают наиболее простые линии пересечения с заданными поверхностями.
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Взаимное пересечение поверхностей
Линия, общая для двух пересекающихся поверхностей — линия пересечения.
Чтобы определить проекцию линии пересечения, необходимо найти проекции точек, общих для этих поверхностей. Их находят способом вспомогательных секущих плоскостей или вспомогательных сфер.
Если рёбра призмы или ось вращения цилиндра перпендикулярны какой-либо из плоскостей проекций, то на этой плоскости проекций линия пересечения совпадает с контуром основания призмы или цилиндра.
Пересечение двух многогранников
Для построения линии пересечения двух многогранников необходимо определить точки пересечения ребер первого многогранника с гранями второго, затем ребер второго с гранями первого. Полученные точки соединить отрезками прямой с учетом видимости. На рисунке 9.2 заданы поверхности трехгранной призмы DEFD’E’F’ и трехгранной пирамиды SABC. Так как призма F, фронтально-проецирующая, фронтальная проекция линии пересечения совпадает с гранями призмы, поэтому необходимо построить только горизонтальную проекцию. Для этого определяем точки пересечения ребер пирамиды с гранями призмы. Ребро SC пересекает грани призмы в точках I и 2, ребро SB — в точках 3 и 4, ребро SA не пересекает призму. Затем определяем точки пересечения ребер призмы с гранями пирамиды.
По чертежу видим, что только ребро DD’ пресекает поверхность пирамиды. Для определения точек пересечения 5 и б через ребро DD’ проводим горизонтальную плоскость, которая пересекает пирамиду по треугольнику. Точки 5 и 6 получаем, как пересечение DD’ с построенным треугольником.
Полученные точки соединяем с учетом видимости. Видимой считается тот отрезок прямой, который принадлежит двум видимым граням поверхностей.
Как видим, линия пересечения двух многогранников представляет собой пространственную ломаную линию.
В том случае, когда обе гранные поверхности общего положения, последовательность соединения точек вызывает затруднение. Поэтому для соединения точек используется диаграмма Ананова — условные развертки поверхностей (см. учебник).
Пересечение гранной и кривой поверхности
Линия пересечения гранной и кривой поверхности, представляет собой пространственную кривую линию, с точками излома на ребрах многогранника.
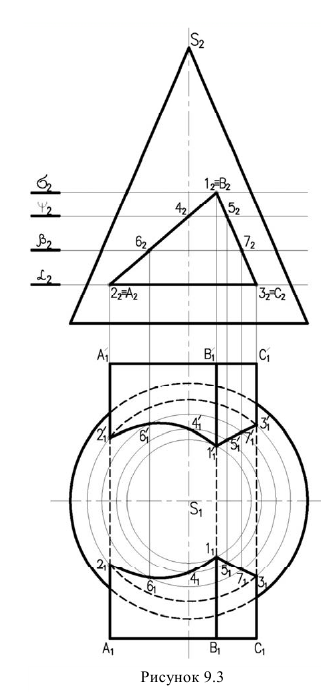
Поэтому сначала определяем точки пересечения ребер многогранника с кривой поверхностью, а затем промежуточные точки и соединяем их с учетом видимости. На рисунке 9.3 заданы поверхности трехгранной призмы и кругового конуса.
Так как призма фронтально-проецирующая, фронтальная проекция линии пересечения совпадает с проекцией боковых граней призмы, поэтому необходимо построить только горизонтальную проекцию линии пересечения.
Сначала определяем точки пересечения ребер призмы 
Пересечение двух кривых поверхностей. Метод вспомогательных секущих плоскостей
Линия пересечения двух кривых поверхностей, представляет пространственную кривую линию. Поэтому для ее построения необходимо определить ряд точек принадлежащих этой лини.
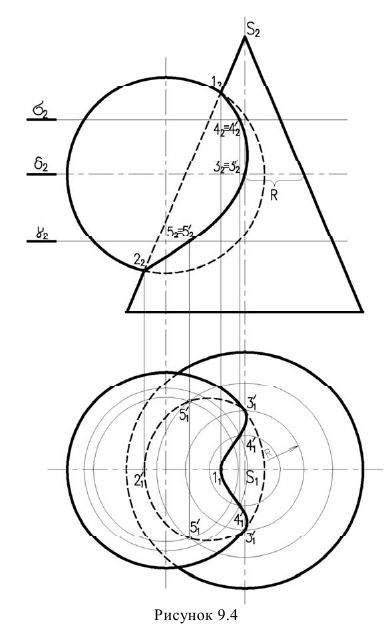
На рисунке 9.4 заданы поверхности конуса и сферы. Точки строятся при помощи горизонтальных плоскостей посредников, которые рассекают обе поверхности но окружностям.
Обязательно находим опорные точки, к которым относятся высшая и низшая точки линии пересечения и точки границы видимости. Так как оси поверхностей лежат в одной фронтальной плоскости, контурные образующие поверхностей пересекаются в точках 1 и 2 — это и будет высшая и низшая точки. Точки границы видимости лежат на экваторе сферы, поэтому точки 3 и 3′ находим с помощью вспомогательной горизонтальной плоскости, проходящей через центр сферы. Она рассекает сферу по экватору, а конус но параллели радиуса R.
Взаимно пересекаясь, они и дают точки 3 и 3′ фронтальную проекцию определяем по вертикальной линии связи на плоскости 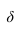
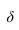
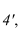
Пересечение поверхностей вращении. Метод вспомогательных секущих сфер
Способ вспомогательных секущих сфер применяется при следующих условиях:
- Пересекающиеся поверхности являются поверхностями вращения.
- Оси этих поверхностей пересекаются.
- Оси поверхностей параллельны одной из плоскостей проекций.
Перед рассмотрением этого способа разберем понятие соосных поверхностей. Соосными называются поверхности вращения, имеющие общую ось. Соосные поверхности пересекаются по окружностям перпендикулярным оси вращения.
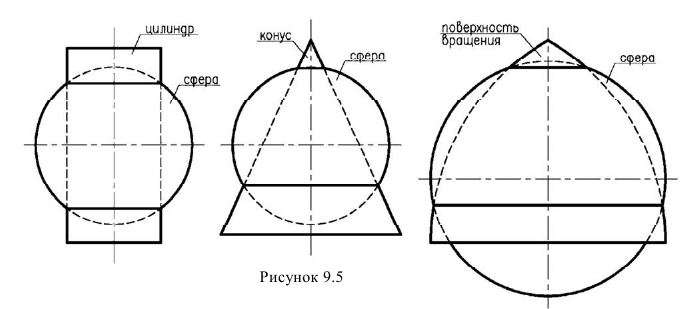
На рисунке 9.5 приведены некоторые из них.
Именно то, что поверхности пересекаются по окружностям, которые проецируются в линии и используется в методе сфер.
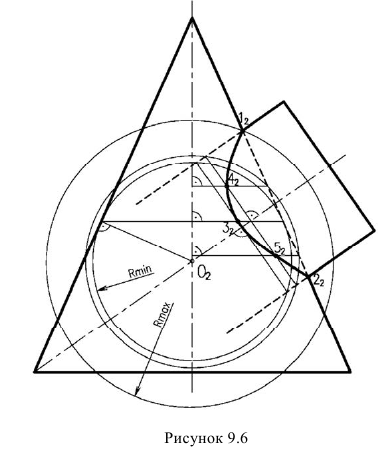
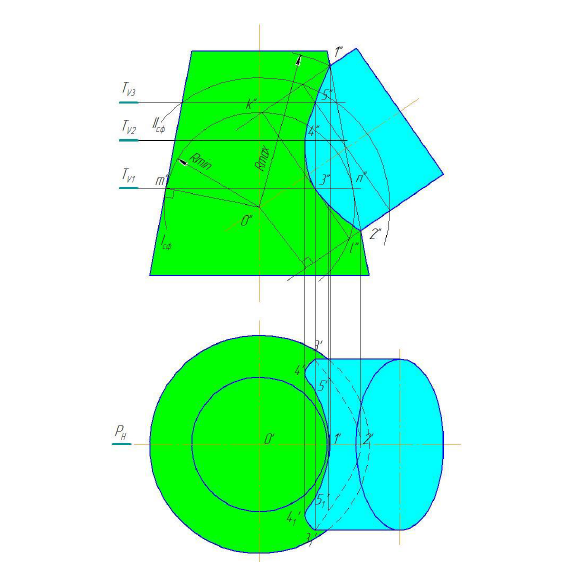
Рассмотрим пример на рисунок 9.6. Даны поверхности вращения — конус и цилиндр. Так как оси лежат в одной плоскости, можно определить точки пересечения контурных образующих в точках 1 и 2, как в предыдущем примере.
Однако, для нахождения промежуточных точек, вспомогательные секущие плоскости не подходят, т.к. горизонтальные плоскости рассекут цилиндр по эллипсам, фронтально-нроецирующие — конус по эллипсам. А сам эллипс строить непросто. Поэтому именно в этом случае удобно использовать в качестве посредников — сферы. За центр вспомогательных сфер, принимается точка пересечения осей заданных поверхностей. Далее необходимо определить, размеры радиусов вспомогательных секущих сфер. Максимальный радиус сферы
— это расстояние от центра сфер до наиболее удаленной точки пересечения контурных образующих (в данном случае точка 1). Минимальный радиус сферы
— радиус сферы, которая вписана в одну из поверхностей, а другую пересекает.
В данном случае минимальная сфера вписана в конус. Минимальная сфера касается поверхности конуса по окружности, а цилиндр пересекает по окружности. Нужно, иметь ввиду, что проекции окружностей пересечения перпендикулярны осям вращения. Эти две окружности пересекаются в точке 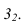
Они пересекают и поверхность цилиндра, и поверхность конуса по окружностям, которые пересекаясь даюг промежуточные точки. Полученные точки соединяются плавной линией.
Здесь построена только фронтальная проекция. Для построения горизонтальной проекции, если это необходимо, точки строят как лежащие на окружностях полученных радиусов.
Теорема Монжа
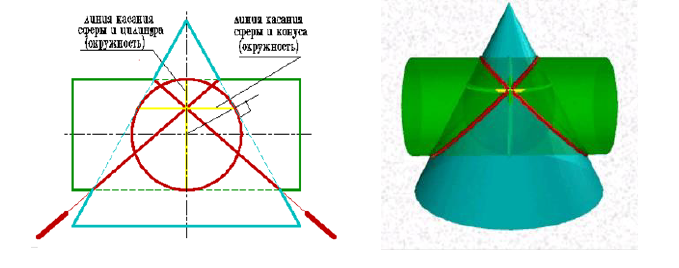
Рассмотрим вариант, когда минимальная сфера касается двух поверхностей вращения. В этом случае для построения линии пересечения поверхностей используется теорема Г. Монжа, которая формулируется так:
Если две поверхности вращении второго порядка описаны около третьей или вписаны в нее, то линии их пересечении распадается на две плоские кривые второго порядка. Плоскости этих кривых проходит через прямую, соединяющую точки пересечении линий касании.
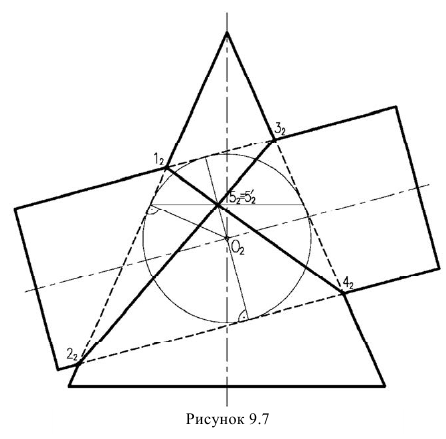
В соответствии с этой теоремой линии пересечения конуса и цилиндра описанного около сферы (рисунок 9.7) будут плоскими кривыми -эллипсами, фронтальные проекции которых изображаются прямыми 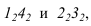
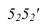
Пересечение поверхностей вращения с многогранниками
Внешние и внутренние формы большинства предметов образуются сочетанием нескольких поверхностей. Пересекаясь между собой, они образуют линии, которые принято называть линиями перехода.
На рис. 9.1 изображена деталь с несколькими линиями перехода. Линия 1 является границей между плоской и торовой поверхностями, 2 — торовой и конической, 3 — конической и плоскими (гранями призмы), 4 и 5 — торовой поверхностью корпуса и цилиндрическими поверхностями патрубков.
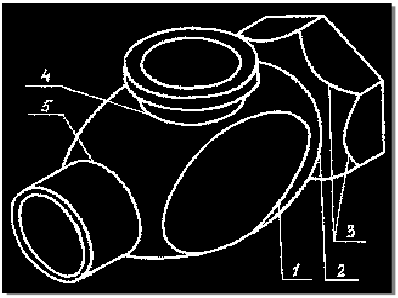
Линия пересечения многогранника с телом вращения в общем случае состоит из отдельных участков кривых линий, получающихся при пересечении граней многогранника с поверхностью вращения. Точки перехода от одного участка к другому находятся в пересечении ребер многогранника с телом вращения и называются точками излома. Участок линии пересечения может быть и прямой линией в случае пересечения линейчатой поверхности вращения гранью многогранника по образующей.
При проницании (полном пересечении) получаются две замкнутые линии пересечения. Они могут быть плоскими (поверхность вращения проницает одну грань) или пространственными, состоящими из нескольких плоских кривых с точками излома в местах пересечения поверхности вращения ребрами многогранника.
При врезании (неполном пересечении) получается одна замкнутая пространственная линия.
Таким образом, в соответствии с указанным выше, задачи данной темы решаются по следующему плану:
- Определяются точки излома линии пересечения, являющиеся точками пересечения ребер многогранника с поверхностью вращения;
- Находятся точки принадлежащие линиям пересечения отдельных граней многогранника с телом вращения. При этом сначала следует найти характерные (опорные) точки кривых. Это точки, проекции которых отделяют видимую часть проекции линии пересечения от невидимой, это проекции наивысших и наинизших точек линии пересечения, ближайших и наиболее удаленных, крайних слева и справа на проекциях линии пересечения;
- Определение видимости линии пересечения поверхностей и их очерков. Видимость проекций участков линии пересечения определяется из условия расположения их на видимой стороне каждой поверхности.
При построении точек линии пересечения многогранников с телами вращения используют вспомогательные секущие плоскости. Их располагают так, чтобы они пересекали данные поверхности по простым для построения линиям (прямым или окружностям).
Рассмотрим линии пересечения поверхности прямой трехгранной призмы с поверхностью конуса вращения. Боковые грани призмы являются фронтально-проецирующими плоскостями, а ось конуса перпендикулярна горизонтальной плоскости проекций.
Призму можно рассматривать, как три плоскости, проходящие через ее грани, а задача сводится к нахождению линий пересечения этих плоскостей с конусом.
Рисунок 9.2 — Пересечение трехгранной призмы с конусом
Пример. Построить линию пересечения поверхности тора с поверх-ностью трехгранной призмы (рис. 9.3).
Решение. Боковые грани призмы являются фронтально-проецирующими плоскостями и фронтальная проекция линии пересечения совпадают с проекцией боковой поверхности призмы. Из фронтальной проекции видно, что в данном случае имеет место проницание тора призмой (две замкнутые линии пересечения).
На рис. 9.3 рассмотрен пример пересечения поверхностей тора и треугольной призмы [2].
По двум заданным проекциям строим третью – профильную.
Рисунок 9.3 – Построение линии пересечения трехгранной призмы с тором
Заданная призма – горизонтально-проецирующая. Так как грани призматического отверстия перпендикулярны горизонтальной плоскости проекций, то на чертеже известна горизонтальная проекция линии пересечения, она совпадает с вырожденной проекцией поверхности призмы.
Следовательно, линия пересечения совпадает с горизонтальной проекцией основания призмы.
Определяем характерные точки: самую близкую точку 1 фронтальной плоскостью 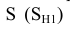
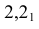
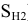
Определяем промежуточные точки 4 и 5 при помощи вспомогательных фронтальных плоскостей 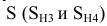
Соединяем полученные точки плавной кривой линией с учетом видимости.
Пересечение поверхностей вращения
Линия пересечения двух поверхностей вращения в общем случае представляет пространственную кривую, которая может распадаться на две и более части. Эти части могут быть, в частности, и плоскими кривыми и даже прямыми линиями.
Линию пересечения поверхностей обычно строят по ее отдельным точкам. Точки подразделяются на характерные (опорные) и промежуточные (случайные).
Общим способом построения этих точек является способ вспомогательных секущих поверхностей – посредников. При пересечении данных поверхностей вспомогательной поверхностью определяются линии пересечения ее с данными поверхностями, в пересечении этих линий получаются точки, принадлежащие искомой линии пересечения.
Наиболее часто в качестве поверхностей-посредников применяются плоскости или сферы.
Для определения линии пересечения часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.
Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.
Из общей схемы построения линии пересечения поверхностей выделяют два основных метода — метод секущих плоскостей и метод секущих сфер.
Способ вспомогательных секущих плоскостей
В качестве вспомогательных секущих плоскостей чаще всего используют плоскости, параллельные одной из плоскостей проекций.
Положение их выбирают таким, чтобы они пересекали заданные поверхности по простейшим линиям – прямым или окружностям.
Этот способ рекомендуется применять, если сечениями заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:
- Если образующие (окружности) расположены в общих плоскостях уровня;
- Если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;
- Линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.
Пересечение цилиндрической и торовой поверхности
Если одна из поверхностей является цилиндрической проецирующей поверхностью, то построение линии пересечения упрощается, так как в этом случае одна проекция линии пересечения совпадает с окружностью – проекцией цилиндра на перпендикулярную плоскость проекций.
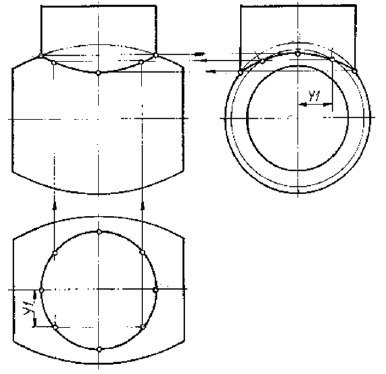
На рис. 9.4 построена линия перехода между цилиндром и тором. Так как поверхность цилиндра перпендикулярна плоскости Н, то горизонтальная проекция линии перехода известна. Она совпадает с горизонтальной проекцией цилиндра. Фронтальную и профильную проекции строим по принадлежности точек линии перехода не проецирующей поверхности тора.
Рисунок 9.4 — Построение линии пересечения цилиндра с тором
Линия пересечения заданных поверхностей представляет собой пространственную кривую линию, имеющую фронтальную плоскость симметрии, образованную пересекающимися поверхностями цилиндра и тора.
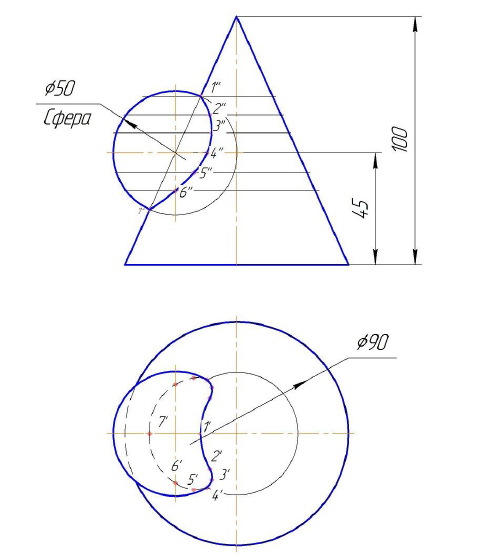
Рассмотрим линию пересечения поверхности сферы с поверхностью конуса вращения (Рисунок 9.5).
Точки 1 и 7, расположенные на очерках фронтальных проекций конуса и сферы, очевидны и определяются без дополнительных построений.
Точка 4 на экваторе сферы построена с помощью горизонтальной плоскости, пересекающей конус по окружности. В пересечении горизонтальных проекций этой окружности и экватора находится горизонтальная проекция 4′ точки 4 и фронтальная 4» проекции точки 4 определим с помощью линии связи. Точка 4 на горизонтальной проекции разделяет кривую на видимую и невидимую части.
Точки 2, 3, 5 и 6, расположенные в промежутке между характерными точками 1,4 и 7 строим аналогично. С помощью линий связи определим фронтальные и горизонтальные проекции этих точек.
Рисунок 9.5 — Построение линии пересечения конуса и сферы
Особые случаи пересечения
Пересечение соосных поверхностей вращения
Соосными называют поверхности вращения, оси которых совпадают. Линия пересечения таких поверхностей строится на основании теоремы о пересечении соосных поверхностей вращения: соосные поверхности вращения пересекаются между собой по окружностям.
Если ось вращения соосных поверхностей перпендикулярна к какой либо плоскости проекций, то линия их пересечения проецируется на эту плоскость в виде окружности, а на другую плоскость проекций – в прямую линию.
На рис. 9.6 даны примеры пересечения соосных поверхностей вращения (ось вращения параллельна горизонтальной плоскости). На рис. 9.6, а приведены сфера и конус, б – сфера и цилиндр, в – сфера и тор.
Рисунок 9.6 — Пересечение соосных поверхностей вращения
Теорема Монжа для пересекающихся поверхностей вращения
Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания.
Для этого случая пересечения поверхностей вращения необходимо выполнение трех условий:
- пересекающиеся поверхности должны быть поверхностями вращения;
- оси поверхностей должны пересекаться;
- плоскость, образованная осями поверхностей, должна быть параллельна одной из плоскостей проекций.
Рисунок 9.7 — Пересечение поверхностей вращения по теореме Монжа
Это положение подтверждается теоремой Монжа: Если две поверхности второго порядка могут быть вписаны или описаны около третьей поверхности второго порядка, то пространственная кривая их пересечения четвертого порядка распадается на две плоские кривые второго порядка.
Способ вспомогательных секущих сфер
При построении линии пересечения поверхностей вращения не всегда удается подобрать секущие плоскости так, чтобы они пересекали поверхности по линиям, проекции которых были бы прямыми или окружностями. В некоторых таких случаях в качестве секущих поверхностей (посредников) целесообразно применять сферы. Этот способ основан на свойстве сферы пересекаться с любой поверхностью вращения, ось которой проходит через центр сферы по окружности.
Чтобы сфера одновременно пересекала две поверхности по окружностям, проецирующимся в прямые линии, необходимо выполнить условия:
- Оси поверхностей вращения должны пересекаться (точку пересечения принимают за центр вспомогательных концентрических сфер).
- Оси поверхностей вращения должны располагаться параллельно какой-либо плоскости проекций.
Пример. Построить проекции линии пересечения поверхностей конуса и цилиндра (рис. 9.8) [1].
Заданы прямой усеченный конус и наклонный цилиндр – тела вращения. Их оси параллельны фронтальной плоскости проекций и пересекаются в точке О(о′,о), т.е. соблюдены условия метода сфер.
Как и в предыдущих задачах, найдем проекции характерных точек. Точка 1 – самая высокая, точка 2 – самая низкая. Чтобы убедится в этом проведем через оси тел вспомогательную фронтальную плоскость 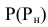
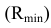
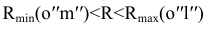
Рисунок 9.8 — Построение линии пересечения конуса и цилиндра
Учитывая, что сфера минимального радиуса всегда касается той поверхности, которая пронизывается другой, соединим найденные фронтальные проекции плавной кривой. Получим фронтальную проекцию линии пересечения. В нашем случае сфера радиусом 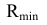
Построим горизонтальную проекцию линии пересечения. Т.к. точки 1′′, 2′′ лежат на очерковой образующей конуса, то горизонтальные проекции этих точек находятся на оси конуса, т.е. на горизонтальной проекции этой образующей. Для нахождения горизонтальных проекций точек 3′, 4′, 5′ воспользуемся горизонтальными плоскостями 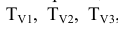
Для правильного соединения точек определим их видимость. Границей видимости на плоскости Н является точка 4′′, лежащая на осевой фронтальной проекции цилиндра. Горизонтальные проекции ее 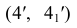
Способ вспомогательных секущих плоскостей
Суть способа — вспомогательная секущая плоскость одновременно пересекает поверхности каждого тела и образует фигуры сечения, контуры которых пересекаются. Точки пересечения контуров соединяют.
Этот способ применим тогда, когда контуры отдельных сечений представляют прямые линии или окружности.
Точки 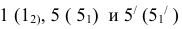
Проведём горизонтальную плоскость 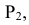
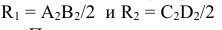
На пересечении этих окружностей сечений на 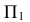
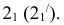
Проведём еще ряд горизонтальных секущих плоскостей и определим проекции других промежуточных точек линии пересечения, которые соединим лекальной кривой с учётом видимости.
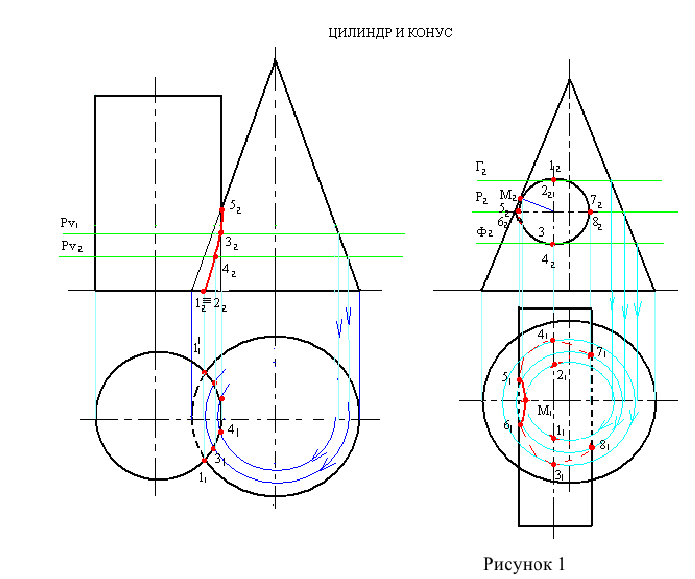
При взаимном пересечении конуса и цилиндра (рисунок 1) ось вращения цилиндра перпендикулярна 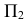
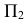
Построив горизонтальную проекцию линии пересечения, на 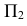
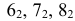
На 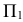
Способ вспомогательных сфер
Этот метод можно применять при соблюдении следующих условий :
- пересекающиеся поверхности должны быть поверхностями вращения;
- их оси должны пересекаться ; точка пересечения осей является центром вспомогательных сфер;
- их оси должны быть // какой-либо плоскости проекций.
Сфера 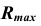
Сфера 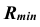
Сфера 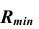
Сфера пересекает тела по окружностям, проецирующимся на одну из плоскостей проекций отрезком.
1. Определяем очевидные точки
2. Восстанавливаем перпендикуляры из центра сфер 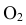
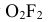
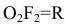
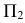
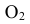
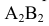
На пересечении этих сечений определяем фронтальную проекцию точки 3 — 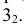
3. На 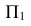
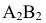
1. Проводим ещё ряд секущих сфер радиусом больше минимальной и меньше максимальной и определяем другие промежуточные точки линии пересечения, которые соединяем лекальной кривой с учётом видимости.
Большее тело поглощает меньшее.
2. Видимость линии пересечения определяем следующим образом:
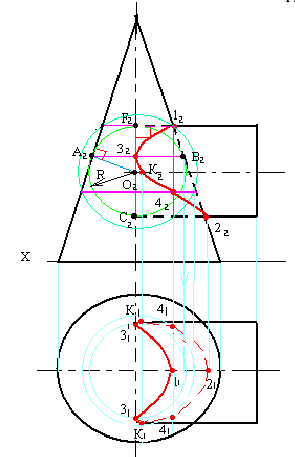
- — на пересечении фронтальной проекции линии пересечения с осью симметрии цилиндра намечаем точку
определяем на
на очерковых образующих цилиндра);
- — часть линии, находящаяся выше точки К — видимая. Точка К — граница видимости.
Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Элементы технического рисования
Технический рисунок — это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз, соблюдая пропорции. Им пользуются на производстве для иллюстрации чертежей.
Обычно технический рисунок выполняется в изометрии.
Выполнение рисунка модели или детали начинается с проведения аксонометрических осей. Затем рисуется основание и строятся габаритные очертания -прямоугольные параллелепипеды. Деталь мысленно расчленяют на отдельные геометрические элементы, постепенно вырисовывая все элементы.
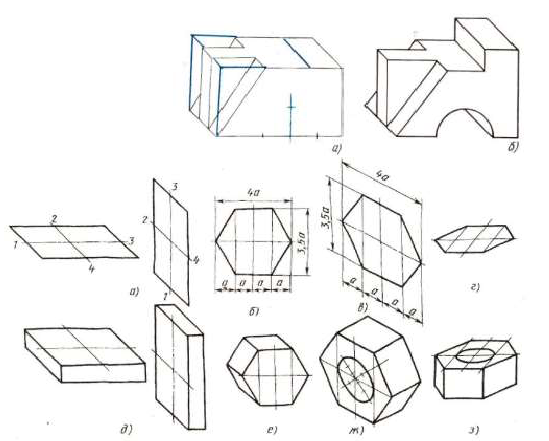
Технические рисунки получаются более наглядными, если их покрыть штрихами. При нанесении штрихов считают, что лучи света падают на предмет справа и сверху или слева и сверху.
Видео:Уравнения кривых в пространствеСкачать

Взаимное пересечение поверхностей с примерами
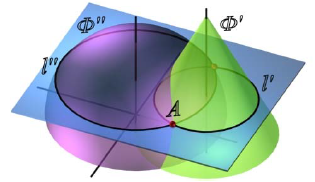
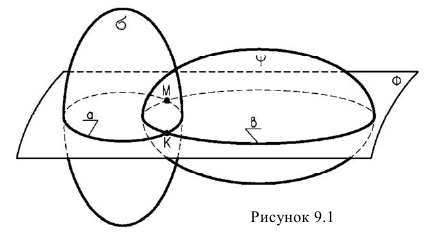
Алгоритм решения задач по определению линии пересечения поверхностей Ф’ и Ф» (рис. 9.1) в целом аналогичен решению второй позиционной задачи и состоит в следующем:
- Обе заданные поверхности Ф’ и Ф» рассекают третьей, вспомогательной плоскостью или поверхностью P.
- Определяют линии пересечения каждой заданной поверхности со вспомогательной: Ф’ × P =l’, Ф» × P =l».
- Определяют точки пересечения полученных линий l’×l» = A и A’. Точки A и a´ принадлежат обеим поверхностям.
- Проведя несколько вспомогательных поверхностей, находят достаточное количество точек и соединяют их плавной лекальной кривой, которая и является искомой линией пересечения поверхностей.
- Определяют видимость поверхностей и линии их пересечения.
Рис. 9.1. Пересечение поверхностей
В качестве вспомогательных поверхностей P следует выбирать поверхности — плоскости или сферы, которые пересекают обе заданные поверхности по наиболее простым для построения линиям — прямым или окружностям. Кроме того, если в сечении поверхности получаются окружности, они должны проецироваться на одну из плоскостей проекций без искажения.
Определение точек линии пересечения поверхностей начинают с построения так называемых опорных точек. К ним относятся:
- точки пересечения очерковых образующих, если образующие лежат в одной плоскости,
- точки, лежащие на очерковых образующих поверхностей,
- точки, лежащие в общей плоскости симметрии,
- экстремальные (верхние — нижние, правые — левые) по отношению к плоскостям проекций, к центру концентрических сфер.
При соединении точек следует иметь ввиду, что проекции линии пересечения не могут выходить за пределы общей площади — площади наложения — проекций пересекающихся поверхностей. Видимыми будут те участки линии пересечения, которые принадлежат видимым частям обеих поверхностей.
Способ вспомогательных параллельных плоскостей
Этот способ заключается в том, что обе поверхности рассекаются параллельными плоскостями уровня. Этот способ применяют лишь в тех случаях, когда вспомогательные плоскости рассекают поверхности по простым линиям — прямым или окружностям, которые проецируются на соответствующую плоскость проекций без искажения.
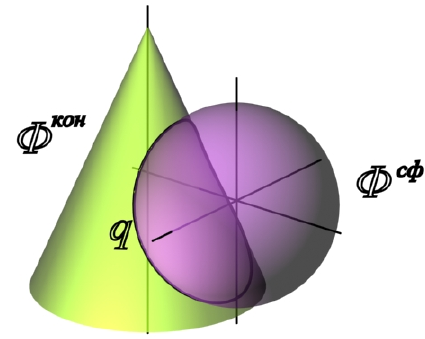
Рассмотрим построение линии пересечения прямого кругового конуса и сферы (рис. 9.2).
Рис. 9.2. Линия пересечения поверхностей прямого кругового конуса и сферы
Фронтальные плоскости уровня пересекают поверхность конуса по гиперболам, следовательно, для решения данной задачи нужно применить горизонтальные плоскости уровня, которые рассекают обе данные поверхности по окружностям.
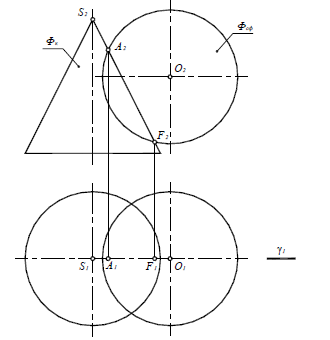
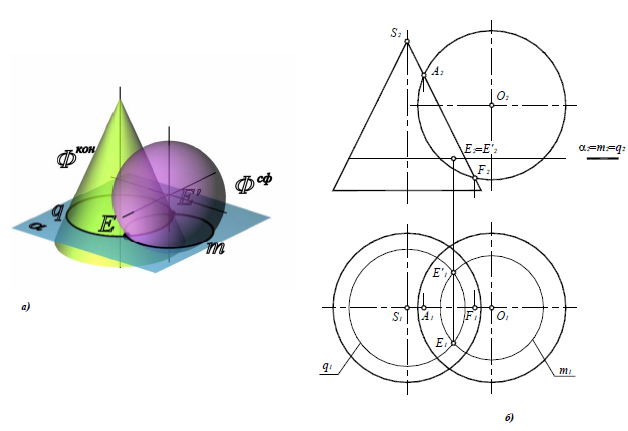
Решение задачи начинают с построения опорных точек. Конус и сфера имеют общую плоскость симметрии γ(γ1), параллельную плоскости П2. Поэтому высшая точка A и низшая точка F линии пересечения получаются как результат пересечения очерковых образующих конуса и сферы (рис. 9.3).
Остальные точки определяются с помощью горизонтальных плоскостей уровня. Более подробно разберем построение точек E и E'(рис. 9.4).
1. Пересечь обе поверхности вспомогательной горизонтальной плоскостью уровня α(а2). Плоскость а(а2) пересекает сферу по окружности m(m1,m2), а конус — по окружности q(q1,q2):
m(m1 ,m 2)=Ф сф 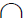
q(q1 ,q2) =Ф к 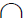
2. Построив горизонтальные проекции окружностей m и q, определить точки их пересечения E и E’:
E1= m1 × q1; E2=E1E2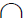
E’1=m1 × q1; E’2=ElE2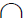
Рис. 9.3. Определение опорных точек линии пересечения поверхностей
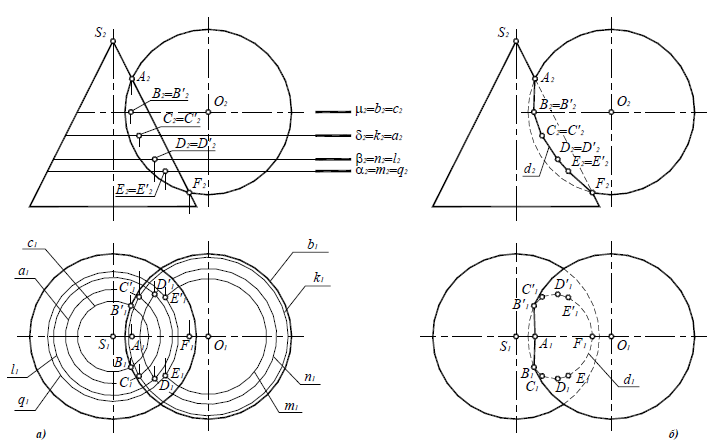
3. Аналогичным образом определяются остальные точки, формирующие линию пересечения (рис. 9.5,а). Они получены с помощью горизонтальных плоскостей уровня β(β2), δ(δ2) и μ(μ2). Пределы этих плоскостей по высоте определяют высшая и низшая опорные точки линии пересечения поверхностей. Плоскость μ(μ2)рассекает поверхность сферы по очерковой образующей b (b2, b2),поэтому полученные точки В и В’ являются опорными, ограничивающими линию пересечения поверхностей по ширине.
4. Последовательно соединить одноименные проекции полученных точек плавной лекальной кривой. Полученная линия не должна выходить за пределы области перекрытия проекций данных поверхностей.
5. Определить видимость линии пересечения поверхностей и их очерковых образующих.
Поверхность конуса на горизонтальной плоскости проекций полностью видима, следовательно, видимость линии пересечения определяется по поверхности сферы. Видима будет та часть сферы, которая на П2 лежит выше очерковой образующей b2.Точки В и В’ на очерковой образующей сферы являются точками смены видимости линии пересечения на плоскости проекций П1.
Искомая линия пересечения поверхностей конуса и сферы d(d1,d2) (кривая второго порядка), полученная способом вспомогательных секущих плоскостей, приведена на рис 9.5,б.
Рис. 9.4. Определение промежуточных точек линии пересечения поверхностей:
а — наглядное изображение;
б — комплексный чертеж
Рис. 9.5. Определение линии пересечения поверхностей способом вспомогательных параллельных плоскостей:
а — определение промежуточных точек;
б — искомая линия пересечения
Способ вспомогательных сфер
При построении линии пересечения двух поверхностей способом вспомогательных сфер возможны два случая. В одном из них используются сферы, проведенные из одного, общего центра (концентрические), а в другом -сферы, проведенные из разных центров (эксцентрические).
Способ концентрических сфер
Этот способ применяется для построения линии пересечения поверхностей вращения произвольного вида, при условии, что оси этих поверхностей пересекаются.
В основу способа концентрических сфер положено свойство сферы с центром на оси какой-либо поверхности.
Если центр сферы находится на оси любой поверхности вращения, то сфера соосна с поверхностью вращения и в их пересечении получатся окружности (рис. 9.6).
Рис. 9.6. Соосные поверхности вращения:
a- наглядное изображение;
б — на комплексном чертеже
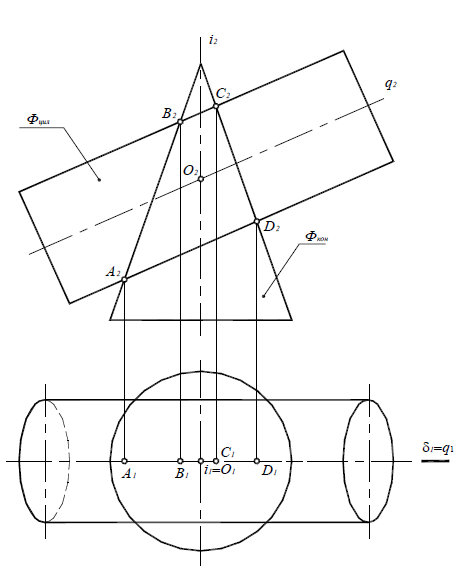
Рассмотрим способ концентрических сфер на примере построения линии пересечения цилиндра и конуса вращения, оси которых i(i1,i2) и q(q1,q2) пересекаются и точка пересечения осей обозначена через O (O1 ,O2)(рис. 9.7).
Рис. 9.7. Линия пересечения поверхностей цилиндра и прямого кругового конуса
Точка пересечения осей поверхностей принимается за центр вспомогательных концентрических сфер.
Алгоритм решения задачи об определении линии пересечения поверхностей состоит в следующем:
1. Определить опорные точки (рис. 9.8). Так как обе данные поверхности имеют общую плоскость симметрии δ(δ1), параллельную плоскости проекций П2, то их очерковые образующие, по отношению к плоскости П2,пересекаются. Точки A(A1,A2), B(B1,B2), C(C1,C2) и D(D1,D2) пересечения этих образующих являются точками видимости линии пересечения поверхностей.
2. Определить радиусы максимальной и минимальной сфер, необходимых для определения точек линии пересечения.
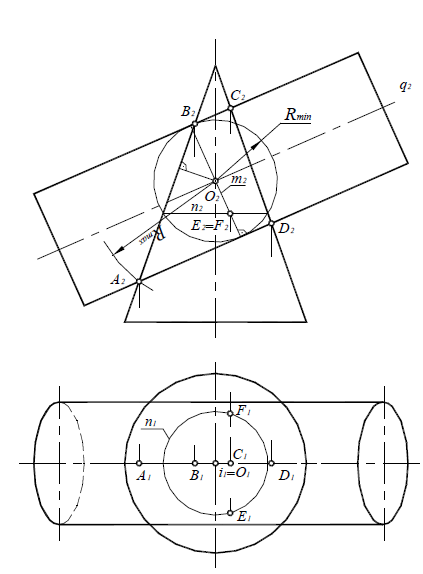
Радиус максимальной сферы Rmax равен расстоянию от центра вспомогательных сфер до наиболее удаленной точки пересечения очерковых образующих, в данном случае Rmax=O2A2 (рис. 9.9).
Чтобы определить радиус минимальной сферы Rmin, необходимо провести через точку O2 нормали к очерковым образующим данных поверхностей. Тогда больший из отрезков этих нормалей и будет Rmin. В этом случае сфера минимального радиуса будет касаться одной из данных поверхностей, а со второй — пересекаться.
В данном случае сферой минимального радиуса является сфера, касающаяся цилиндрической поверхности (см. рис. 9.9).
Сфера радиусом Rmin касается цилиндрической поверхности по окружности m, которая на фронтальной проекции изображается в виде прямой m2, перпендикулярной q2(m2

Чтобы построить горизонтальные проекции точек Е и F следует воспользоваться окружностью n, содержащей данные точки, так как она не искажается на плоскости проекций П1:
Рис. 108. Определение опорных точек линии пересечения поверхностей
Рис. 9.9. Определение радиусов максимальной и минимальной сфер.
Для построения промежуточных точек линии пересечения проводят несколько концентрических сфер с центром в точке O, причем радиус R этих сфер должен изменяться в пределах Rmin
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📽️ Видео
Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Лекция 12. Пересечение поверхностей метод плоскостейСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Пересечение поверхностей. Построение линии пересечения.Скачать

Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Линия пересечения двух поверхностей конус и призма (Метод секущих плоскостей)Скачать

Поверхности второго порядкаСкачать













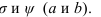
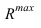 — это расстояние от центра сфер до наиболее удаленной точки пересечения контурных образующих (в данном случае точка 1). Минимальный радиус сферы
— это расстояние от центра сфер до наиболее удаленной точки пересечения контурных образующих (в данном случае точка 1). Минимальный радиус сферы 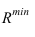 — радиус сферы, которая вписана в одну из поверхностей, а другую пересекает.
— радиус сферы, которая вписана в одну из поверхностей, а другую пересекает.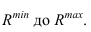
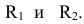
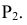
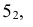
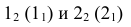
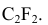
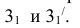
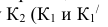 определяем на
определяем на 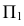 на очерковых образующих цилиндра);
на очерковых образующих цилиндра);