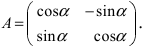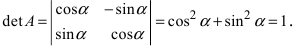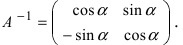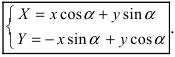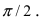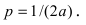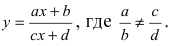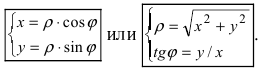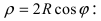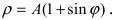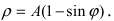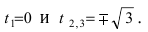Уравнение кривой из полярной в декартовую систему (4 видео)

Содержание

Преобразования декартовой системы координат с примерами решения
Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
Полярные координаты. Замечательные кривые
Уравнения кривых.
Упражнения
🔥 Видео

Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Преобразования декартовой системы координат с примерами решения

Содержание:

Видео:Построение кривой в полярной системе координатСкачать

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

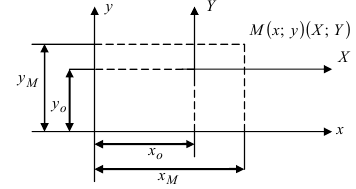
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 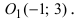Вычислить положение точки М в новой системе отсчета.

Решение:

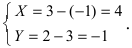
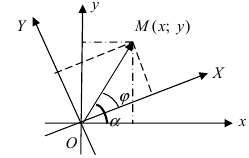
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 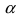(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

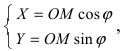
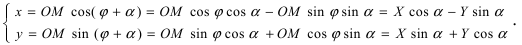
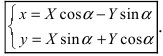
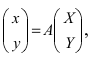
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 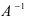обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

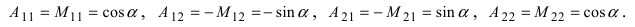
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 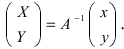Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 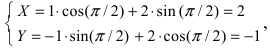т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

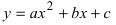
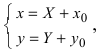
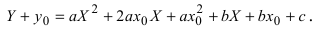
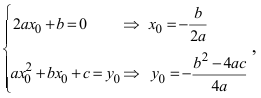
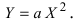
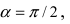
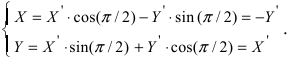
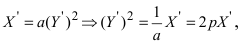
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 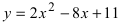к каноническому виду.

Решение:

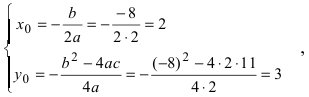
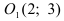
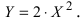
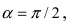
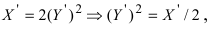
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

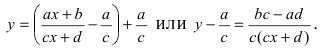
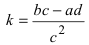
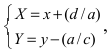
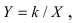
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

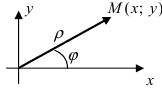
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 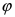между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

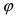
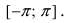
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

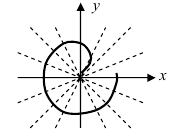
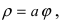
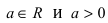
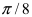
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

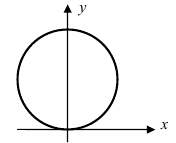
2. Уравнение окружности: уравнение 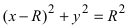описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

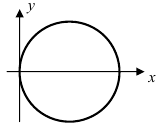
3. Уравнение 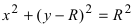описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

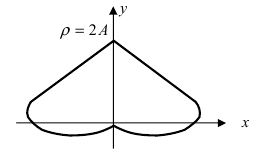
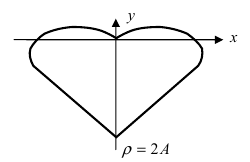
4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

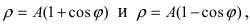
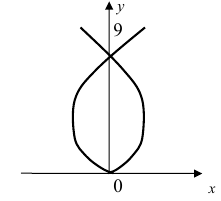
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

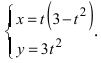
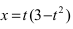
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Бесконечно малые и бесконечно большие функции
Замечательные пределы
Непрерывность функций и точки разрыва
Точки разрыва и их классификация
Экстремум функции
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Скалярное произведение и его свойства
Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Уравнения кривых.

В аналитической геометрии всякому уравнению вида F(x; у) = 0 может соответствовать некоторая линия, свойства которой определяются данным уравнением.

Под F(x; у) = 0 понимаем многочлен степени n; степень многочлена n – порядок линии.

Значит, кривая первого порядка, в декартовой системе координат, описывается алгебраическим уравнением первого порядка ax + by + c = 0, где хотя бы один из коэффициентов a или b отличен от нуля. Это уравнение называют также линейным уравнением. А само выражение, типа ax+by+c=0 и a 2 +b 2 ≠ 0, принято обозначать как общее уравнение прямой.

Следовательно, любая прямая на плоскости представляет собой алгебраическую кривую первого порядка и любая алгебраическая кривая первого порядка на плоскости есть прямая.

Общее уравнение кривой второго порядка в декартовых координатах имеет вид:

причем, в зависимости от значения произведение аb получаем:

— эллипс, частный случай — окружность ( когда ab > 0);

Видео:Полярная система координатСкачать

Упражнения

1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .

2. Нарисуйте кривую, задаваемую уравнением r = cos φ .

3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

4. Докажите, что уравнение

задает эллипс, если 0 > 1.

5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?

6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?

7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = .

8. Нарисуйте спираль Галилея , которая задается уравнением r = a 2 ( a > 0). Она вошла в историю математики в XVII веке в связи с задачей нахождения формы кривой, по которой двигается свободно падающая в области экватора точка, не обладающая начальной скоростью, сообщаемой ей вращением земного шара.

9. Нарисуйте кривую, задаваемую уравнением r = | |.

10. Нарисуйте кривую, задаваемую уравнением r = .

11. Нарисуйте кривую, задаваемую уравнением r = .

12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.

1. Березин В. Кардиоида //Квант. – 1977. № 12.

2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.

3. Берман Г.Н. Циклоида. – М.: Наука, 1975.

4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.

5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.

6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.

7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.

8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.

9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.

10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.