Уравнение косинуса угла между координатной плоскостью оху и плоскостью а1а2а3 (3 видео)

Задача 54757 Даны четыре точки.

Содержание

Условие
Решение
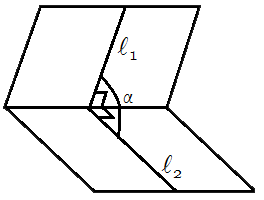
Угол между координатной плоскостью oxy и плоскостью
Что ты хочешь узнать?
Ответ
Проверено экспертом
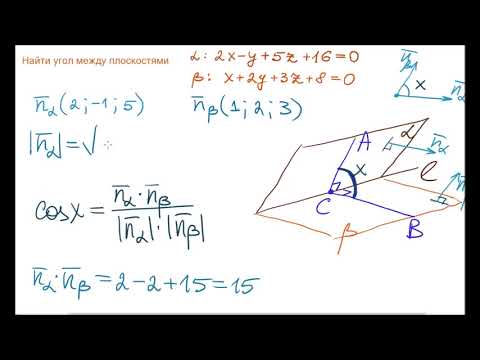
Найти угол между плоскостями
Ввод данных в калькулятор для вычисления угла между плоскостями
Дополнительные возможности калькулятора вычисления угла между плоскостями
Теория. Угол между плоскостями
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
Предупреждение
Угол между плоскостями − теория
Онлайн калькулятор. Угол между плоскостями.
Найти угол между плоскостями
Ввод данных в калькулятор для вычисления угла между плоскостями
Дополнительные возможности калькулятора вычисления угла между плоскостями
Теория. Угол между плоскостями
🔥 Видео

Условие

Даны четыре точки А1(4;2;10),А2(1;2;0),А3(3;5;7),А4(2;-3;5). Вычислить косинус угла между координатной плоскостью Оxy и плоскостью А1А2А3

Решение

Угол между плоскостями равен углу между их нормальными векторами:

При пересечении двух плоскостей образуется пара вертикальных углов.

Угол выбираем наименьший.

Поэтому косинус его положительный, значит в формуле нахождения угла — модуль скалярного произведения

[m] vec<n_<A_A_A_>>=vec=(30;1;-9)[/m] ( см. уравнение плоскости в приложении)

Тогда скалярное произведение векторов:

Пусть M ( x; y; z) – произвольная точка плоскости.

Тогда векторы
vector=(x–4;y–2;z–10)
vector=(–3;0;–10)
vector=(–1;3;-3)
лежат в одной плоскости, а значит КОМПЛАНАРНЫ

Условие компланарности= равенство нулю определителя третьего порядка,
составленного из координат этих векторов:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Угол между координатной плоскостью oxy и плоскостью

Что ты хочешь узнать?

Видео:Угол между векторами | МатематикаСкачать

Ответ

Проверено экспертом

Даны четыре точки А1 (6, 1, 1), А2 (4, 6, 6), А3 (4, 2, 0) и А4 (1, 2, 6).

а) Уравнение плоскости А1, А2, А3 находим на основе смешанного произведения векторов.

x-6 y-1 z-1 x-6 y-1 x-6 y-1 z-1 x-6 y-1

4-6 6-1 6-1 4-6 6-1 -2 5 5 -2 5

4-6 2-1 0-1 4-6 2-1 = -2 1 -1 -2 1 =

= (x – 6)*((-5) -5) + (y – 1)*(-10-2) + (z – 1)*(-2 + 10) =

= -10x – 12y + 8z + 64 = 0. Сократим на -2:

Уравнение плоскости А1А2А3 равно 5x + 6y – 4z – 32 = 0.

б) Уравнение прямой А1, А2: (x – 6)/(-2) = (y – 1)/5 = (z – 1)/5.

в) Прямой А4, М, перпендикулярной к плоскости А1, А2, А3.

Нормальный вектор плоскости А1А2А3 (5; 6; – 4) – это направляющий вектор прямой, перпендикулярной к этой плоскости.

Получаем уравнение прямой А4М: (x -1)/5 = (y – 2)/6 = (z – 6)/(-4).

г) Прямой А4, N, параллельной прямой А1, А2.

д) Синус угла между прямой А1, А4 и плоскостью А1, А2, А3.

Вектор А1А4:(-5; 1; 5), его модуль равен √(25+1+25) = √51.

Нормальный вектор плоскости А1А2А3 (5; 6; – 4), его модуль равен √(25+36+16) = √77. Скалярное произведение равно -25+6-20 = -39.

sin fi = |-39|/(√51*√77)= 0,62234923

fi = 0,67174 радиан, 38,4879 градус.

ж) Косинус угла между координатной плоскостью Оxy и плоскостью А1, А2, А3.

Нормальный вектор координатной плоскости Оxy равен (0; 0; 1), его модуль равен 1. Нормальный вектор плоскости А1А2А3 (5; 6; – 4), его модуль равен √77.

cos a = |0*5+0*6+1*(-4)|/(1*√77) = 4/√77 ≈ 0,455842.

Предлагаю вам воспользоваться онлайн калькулятором для вычисления угла между плоскостями.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между плоскостями и закрепить пройденный материал.

Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Найти угол между плоскостями

Уравнение 1-ой плоскости:

Уравнение 2-ой плоскости:

Ввод данных в калькулятор для вычисления угла между плоскостями

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления угла между плоскостями

Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Угол между плоскостями

Двугранный угол между плоскостями равен углу образованному их нормальными векторами.

Если заданы уравнения плоскостей A₁ x + B₁ y + C₁ z + D₁ = 0 и A₂ x + B₂ y + C₂ z + D₂ = 0, то угол между плоскостями можно найти, используя следующую формулу

cos α =	\|A₁·A₂ + B₁·B₂ + C₁·C₂\|
√ A₁ 2 + B₁ 2 + C₁ 2 √ A₂ 2 + B₂ 2 + C₂ 2

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!

С помощю этого онлайн калькулятора можно найти угол между плоскостями. Дается подробное решение с пояснениями. Для вычисления угла между плоскостями, введите элементы уравнения плоскостей в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Угол между плоскостями − теория

Пусть заданы две плоскости α и β общими уравнениями

A₁x+B₁y+C₁z+D₁=0,

(1)

A₂x+B₂y+C₂z+D₂=0

(2)

Из определения скалярного произведения, имеем

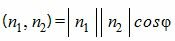Уравнение косинуса угла между координатной плоскостью оху и плоскостью а1а2а3

(3)

Тогда из (3) можно найти косинус угла между нормальными векторами n₁ и n₂:

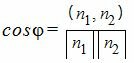(4)

Учитывая, что (n₁, n₂)=A₁A₂+B₁B₂+C₁C₂ и длины векторов |n₁|= и |n₂|=выражение (4) можно записать так:

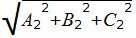
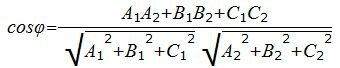(5)

Таким образом косинус угла между нормальными векторами и, следовательно, косинус угла между плоскостями α и β определяется формулой (5). Далее можно найти угол φ с помощью функции arccos.

Отметим, что пересекающиеся плоскости образую два угла. Другой угол можно найти так: φ‘=180−φ.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Онлайн калькулятор. Угол между плоскостями.