Прежде чем рассмотреть кинетику мономолекулярных реакций, необходимо уточнить сам термин «мономолекулярные» применительно к тем процессам, о которых пойдет речь. Как будет видно из дальнейшего, при термическом характере активации такие реакции не могут протекать в одну стадию и, следовательно, являются реакциями сложными. Поэтому, несмотря на традиционное и широкое использование этого термина, здесь его употребление не вполне корректно, и в теории химической кинетики под мономолекулярными обычно подразумевают реакции, в которых участвует только одно исходное вещество. Одной из наиболее простых и удачных схем протекания мономолекулярных реакций стала схема Линдеманна.
В основе схемы Линдеманна лежит предположение о том, что первой стадией этих реакций является, строго говоря, не химическая реакция, а столкновительное взаимодействие — бимолекулярное соударение реагента А с любой частицей (с инертным газом, продуктом реакции и с другой молекулой А в том числе), которое при благоприятных обстоятельствах приводит к ее активации, т.е. приобретению энергии, достаточной для перехода через потенциальный барьер,

Далее активная молекула А* может еще раз столкнуться с М и дезактивироваться, причем в отличие от (1) каждое столкновение приводит к дезактивации

Последнее предположение физически означает равенство константы k1 средней частоте бимолекулярных столкновений Z0, которую легко найти из молекулярно-кинетической теории. Если, однако, такое дезактивирующее столкновение запаздывает, то активная молекула А* может превратиться в продукты реакции
Таким образом, центральным моментом в схеме Линдеманна является идея о бимолекулярных столкновениях как о единственно возможном пути термической активации частиц реагента в мономолекулярных (односубстратных) реакциях.
Используем метод стационарных концентраций и найдем кинетическое уравнение реакции, исходя из записанных выше стадий (1-2) и полагая, что в них М = А. Поскольку концентрация активных молекул А* весьма мала, то можно считать ее стационарной
Тогда скорость реакции, определяемая по расходу реагента А или накоплению продукта Р равна
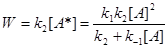
Если давление, а следовательно, и концентрация [А] достаточно велики, так что k-1[A] >> k2 то уравнение (3) перейдет в

т.е. в кинетическое уравнение, отвечающее первому порядку по концентрации реагента А. Напротив, при малых давлениях, когда k2 >> k-1 [А],

и реакция имеет второй кинетический порядок.
Физический смысл этих двух предельных случаев, которым соответствуют кинетические уравнения (4) и (5), вполне ясен в рамках схемы Линдеманна. При малых давлениях вероятность бимолекулярных столкновений невелика, и именно эта стадия является лимитирующей — скорость всего процесса растет пропорционально квадрату концентрации. При больших давлениях, напротив, скорости активации и дезактивации достаточно велики, и лимитирующей стадией становится собственно химическое превращение, а первые две быстрые стадии обеспечивают квазиравновесное распределение частиц по энергиям; здесь скорость реакции пропорциональна первой степени концентрации. Следует также отметить, что во втором случае отношение k1/k-1 в кинетическом уравнении (4) является просто константой равновесия процесса активации.
Таким образом, схема Линдеманна предполагала единый для всех химических реакций с термическим характером активации путь приобретения реагентами избыточной энергии через бимолекулярные столкновения, и в этом состоял ее первый важнейший результат. Во-вторых, она вполне естественным путем объясняла, почему, в мономолекулярных реакциях при варьировании давления в реакционной системе наблюдается изменение кинетического порядка. Если записать уравнение (3) в несколько ином виде
то это же обстоятельство может быть отражено в виде зависимости наблюдаемой константы скорости от концентрации

Общий вид зависимости kэфф = f([A]) приведен на рис. 1.
Рис. 1 . Зависимость наблюдаемой константы скорости мономолекулярной реакции от концентрации реагирующего вещества
Кривые такого типа получали неоднократно, когда исследовали кинетику мономолекулярных реакций в широком интервале концентраций исходных веществ или общих давлений. Эти экспериментальные результаты могли рассматриваться как хорошее качественное подтверждение правильности схемы, предложенной Линдеманном для мономолекулярных реакций.
Эффективную константу скорости, отвечающую наблюдаемой константе скорости реакции 1-го порядка, можно привести к линейному виду в обратных координатах:
Кроме того, время жизни активных молекул можно оценить, как
В то же время детальный количественный анализ констант скорости в модели Линдеманна, определенных на основании кинетических экспериментов, почти сразу же обнаружил существенные расхождения теоретических и опытных величин. В частности, опытным путем можно было установить, при какой концентрации реагента или общем давлении имеет место переход от первого кинетического порядка ко второму; эта концентрация [А] соответствует значению kэфф = k∞/2. С другой стороны, из (6) следует, что

Поскольку к в рамках схемы Линдеманна является константой скорости бимолекулярной реакции (1), то ее вычисляли по уравнению Траутца-Льюиса и далее, найдя теоретическое значение [A]1/2, сравнивали его с экспериментальной величиной. Результат сравнения был не в пользу теории: при варьировании давления первый порядок реакции наблюдали при значительно меньших давлениях, чем предсказывала теория. Иначе говоря, расчетная величина к была очень сильно занижена, в некоторых случаях на несколько порядков. В рамках теории столкновений такой результат означал, что столь же значительны различия между истинными и расчетными величинами сечения химической реакции. Такие существенные различия представлялись малоправдоподобными, если исходить из простой модели столкновений, где реагирующие молекулы рассматриваются как бесструктурные жесткие сферы и где единственным источником активации реагентов является их поступательная энергия, а доля активных столкновений определяется критическим значением кинетической энергии столкновения по линии центров. Кроме того, схема Линдеманна предусматривала временную задержку между актом активации и превращение активированной частицы в продукт, что противоречит величине частоты колебаний двухатомной частицы, а следовательно времени, необходимому для разрыва связи между образующими ее атомами.
Поправка Хиншельвуда
Главная идея Хиншельвуда заключалась в том, что помимо кинетической энергии, которая в результате неупругих столкновений переходит во внутреннюю вращательно-колебательную энергию молекул, эти молекулы сами по себе обладают определенным запасом собственной внутренней энергии; она в принципе также может быть использована для активации. Это предположение вносит существенные коррективы в простую схему Линдеманна. В отличие от последней, где протекание реакции обусловливается превышением кинетической энергией столкновения по линии центров над некоторым пороговым уровнем εа модель Хиншельвуда рассматривает другое, более общее условие: этот порог может быть превышен молекулой А не только за счет энергии столкновения, но и путем перераспределения ее собственной энергии колебаний.
Что касается второй стадии схемы Линдеманна — столкновительной дезактивации, а также третьей стадии — химического превращения, то их константы в теории Хиншельвуда принимаются существенно постоянными.
Итак, по Хиншельвуду, после бимолекулярного столкновения частица А активируется в узкий интервал энергий ε, ε + dε

Если в столкновительной активации принимает участие f колебательных степеней свободы молекулы, то для каждой из них энергия выражается двумя квадратичными членами, соответствующими кинетической и потенциальной энергией осциллятора. Тогда полной колебательной и поступательной энергии, участвующей в этом процессе, отвечают
квадратичных членов. Вероятность попадания энергии молекулы, которая выражается s квадратичными членами, в интервал ε, ε + dε определяется как

Вероятность того, что ε ≥ εа найдем из (10)

При εa/kT >> 1интеграл в правой части (11) приблизительно равен
Поскольку частота всех бимолекулярных столкновений определяется соотношением
z0 =
то частота столкновений, приводящих к активации молекул, т.е. константа скорости активации по Хиншельвуду равна
Выражение в квадратных скобках носит название поправки Хиншельвуда (в уравнении Траутца-Льюиса).
Таким образом, для многоатомных молекул, подбирая число колебательных степеней свободы, которые участвуют в перераспределении энергии при столкновительной активации, можно вполне удовлетворительно согласовать теорию активных столкновений с экспериментом. Положительным моментом модели Хиншельвуда было то обстоятельство, что число таких «активных» степеней свободы f для превращения N-атомных молекул никогда не превышало величину 3N-6(5), т.е. число нормальных колебаний.
Предварительно вернемся к теме предыдущего семинара и обсудим возможные способы расчета газокинетических диаметров сталкивающихся частиц. Значение радиуса частицы, входящего в выражение сечения соударения, можно оцеть по вязкости газа или плотности жидкости:


Смесь брома с этиленом при равных парциальных давлениях в 3 мм рт.ст. имеет температуру 298 К. Рассчитать частоту соударений в единице объема для пар Br2 + Br2, C2H4 + C2H4 и Br2 + C2H4. Принять плотности жидкостей: ρ Br2 = 3,1 г/см 3 , ρ С2Н4 = 0,4 г/см 3 . Молекулярная масса Br2 160 г/моль, С2Н4 28 г/моль.
Вычислить максимально возможную скорость мономолекулярной реакции распада С2Н5Cl при температуре 750 К, давлении 100 мм рт.ст., если энергия молекулы описывается через 2s = 12 квадратичных членов, опытная энергия активации EA = 60800 кал/моль и эффективный диаметр соударений d = 4,5·10 –8 см.
Максимально возможная скорость мономолекулярной реакции по схеме Линдеманна равна первой стадии схемы – скорости активации. Поскольку первая стадия является бимолекулярной , используем формулу Траутца-Льюиса, домноженную на концентрацию для сохранения размерности [время –1 ]. Напомним, что размерность константы при подстановки R в эргах: см 3 /молекула·с; переход от молекулы к молю – путем умножения на число Авогадро, а от см 3 к литрам, — умножением на 10 –3. . Итак:
С – концентрация исходного вещества моль/см 3
Найдем связь между энергией активации по Аррениусу (опытной) и ЕТАС (энергией активации в ТАС). Пусть k1 = const·T 1/2 – ( s – 1) · exp (–ETAC/RT)
Все остальные сомножители вносим в const/
Логарифмируем и берем от левой и правой частей производную по температуре

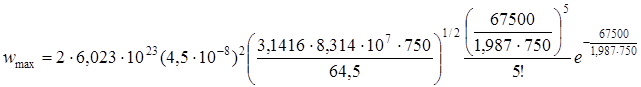
Замечание: Если отсутствует информация о стерическом множителе, его принимают равным единице.
Опытное значение константы скорости разложения N2O
N2O → N2 + ½ O2 при 1085 К и давлении 1,15 атм равно 5,7·10 –4 с –1 . Рассчитайте с помощью теории соударений и схемы Линдеманна энергию активации данной реакции, полагая, что эффективный диаметр столкновений равен 3,3·10 –8 см, а стерический фактор равен единице.
Ответ: ЕТАС = 258,2 кДж/моль
Возможно самостоятельное решение задачи студентами.
1. Оценить энергию диссоциации двухатомной молекулы A-B в газе, состоящем только из молекул AB, если известно, что при 500 о С время полураспада AB составляет 69,18 мин при начальном давлении 2,89 мм рт.ст. и 115,53 мин при 0,57 мм рт.ст. Воспользуйтесь теорией мономолекулярных реакций Линдеманна, приняв значение предэкспоненциального множителя A¥ при Р ® ¥ равным 10 13,5 с — 1 .
2. Константа скорости мономолекулярной реакции разложения:
C3H7N=NC3H7 ® N2 + C6H14 выражается эмпирическим уравнением: k = 5,71×10 13 ×e — 40900/RT . Найти максимально возможное с точки зрения теории соударений значение предэкспоненциального множителя при Т = 563 К, приняв эффективный диаметр молекулы 5×10 — 8 см, концентрацию реагирующего соединения 4,464×10 — 2 моль/л.
3. Термическая изомеризация циклопропана в пропилен изучена при 500 о С и различных начальных давлениях. Экспериментальные данные приведены в таблице:
Ро, мм рт.ст. 2,89 0,57 0,17 0,12 0,10
kэфф.×10 4 , с — 1 1,67 1,00 0,50 0,38 0,33
Здесь kэфф. определяли как начальную скорость, деленную на начальную концентрацию. Определить константы скорости стадий активации и распада активированных молекул, если дезактивация происходит при каждом соударении. Принять величину предэкспоненциального множителя при Р ® ¥ А¥ = 10 13,5 с — 1 .
4. Зависимость эффективной константы скорости мономолекулярной реакции разложения диметилового эфира, протекающей при температуре 777 К, от начальной концентрации дается уравнением: 

- ДЗФКХ07. Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005
- Для мономолекулярных обратимых реакций типа А В дифференциальная форма кинетического уравнения имеет вид
- Для мономолекулярных параллельных реакций типа
- Интегрирование приводит к следующему результату
- Для последовательных реакций первого порядка типа
- Решение этих уравнений приводит к следующим результатам
- 📽️ Видео
Видео:Химическое равновесие. Константа равновесия. 10 класс.Скачать

ДЗФКХ07. Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005
| Название | Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005 |
| Анкор | ДЗФКХ07.doc |
| Дата | 25.05.2018 |
| Размер | 0.71 Mb. |
| Формат файла |  |
| Имя файла | ДЗФКХ07.doc |
| Тип | Методические указания #19623 |
| страница | 4 из 5 |
| Подборка по базе: 4 и 5 задача.docx, 12 04 04 Метод указания к выполнению магистерской диссертации.do, Психология Задачи к семинарам.doc, 15 урок Решение задач.pptx, Вопросы и задачи УЧР 2021 год.odt, ГМУ задачи.docx, Метрология задача №3.docx, 3 курс Задачи ЦНС (1).doc, ЯП1 Задачи экзамен 2022 01 (1).docx, Методические указания тлз заочное Математиика.docx Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать  Для мономолекулярных обратимых реакций типа А В дифференциальная форма кинетического уравнения имеет вид Здесь k 1 – константа скорости прямой реакции, k– 1 – константа скорости обратной реакции. При равновесии Если при t = 0 С B = 0, то справедливы следующие соотношения где С А, С B — текущие концентрации веществ A и B; С А 0 — начальная концентрация A при t = 0; k 1 и k – 1 – константы скоростей прямой и обратной реакций; СА и С В — равновесные концентрации A и B; K – константа равновесия. Интегральная форма кинетического уравнения Видео:Скорость реакции. Химия – ПростоСкачать  Для мономолекулярных параллельных реакций типа
дифференциальная форма кинетического уравнения имеет вид Видео:Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать  Интегрирование приводит к следующему результату где k 1 и k 2 – константы скоростей первой и второй реакций. Константы скоростей отдельных стадий для реакций данного типа определяют по соотношению где x 1 и x 2 – количества моль веществ B и C, образовавшихся к моменту времени t. Видео:Химическая кинетика. Скорость химической реакции | ХимияСкачать  Для последовательных реакций первого порядка типадифференциальные кинетические уравнения имеют вид
Видео:Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать  Решение этих уравнений приводит к следующим результатамгде С А, С B , С D – текущие концентрации веществ А, В и D; С А 0 – начальная концентрация вещества A; k 1 и k 2 – константы скоростей первой и второй стадий. Точка максимума на кинетической кривой С B = f (t) характеризуется уравнениями: где t max – время, соответствующее максимальной концентрации вещества B. В сложных реакциях с участием активных промежуточных частиц используется метод квазистационарных (или стационарных) концентраций. В этих реакциях за малый промежуток времени (мало изменение концентрации исходных веществ) в системе устанавливается режим, при котором разность скоростей образования r o и расходования r p промежуточных частиц становится малой по сравнению с этими скоростями. Такой режим процесса называется квазистационарным, а соответствующие ему концентрации промежуточных частиц — квазистационарными концентрациями. В квазистационаром режиме можно полагать: где Квазиравновесное приближение применяют тогда, когда одна из реакций является обратимой, причем равновесие быстро устанавливается и медленно разрушается. Рассмотрим кинетическую схему: Поскольку равновесие на первой стадии устанавливается быстро, то k 2 k – 1. Тогда концентрацию промежуточного продукта В можно выразить через константу равновесия: Скорость реакции равна: Мы получили уравнение реакции первого порядка. Пример 16. Для обратимого процесса А В константы скоростей прямой и обратной реакций равны соответственно k 1 = 0,4 c – 1 , k 2 = 0,05 c – 1 . Начальные концентрации веществ А и В равны 0,04 моль/л. Определить какими окажутся концентрации этих веществ через 0,2 с.
где x – количество прореагировавшего вещества А, a и b – начальные концентрации веществ А и В. Решение этого уравнения: Здесь При t наступает равновесие, которое характеризуется константой равновесия Вычисляем
Из уравнения (* ) получаем С А = 0,04 – 0,0027 = 0,0373 моль/л; С В = 0,04 + 0,0027 = 0,0427 моль/л. Пример 17. В параллельных реакциях первого порядка: 1. А В ; (k 1 ) Выход вещества В равен 40 %, а время превращения А на 30 % равно 5 мин. Найти k1 и k2. Решение. Кинетическое уравнение для превращения вещества в двух параллельных реакциях первого порядка имеет вид
С учетом превращения вещества А на 30 % получаем уравнение:
где а – начальная концентрация вещества А. Вычисляем
Выход вещества В равен 40 %, следовательно выход вещества D – 60 %. Отношение этих выходов равно отношению конечных концентраций веществ В и D. Следовательно, отношение соответствующих констант скоростей равно: Решаем систему уравнений: Пример 18. В системе осуществляется последовательная реакция Начальная концентрация вещества А равна 1 моль/л, вещества В и D в начальный момент в системе отсутствуют. Константы скорости равны k 1 = 0, 2 мин – 1 и k 2 = 0, 05 мин – 1 . Вычислите: 1) время достижения максимальной концентрации вещества В; 2) максимальную концентрацию вещества В; 3) время достижения концентрации С А = 0,01 моль/л. Решение. 1. Рассчитаем время, которое будет соответствовать максимальной концентрации промежуточного вещества В: 2. Рассчитаем концентрацию вещества А через время t max:
Максимальная концентрация промежуточного вещества равна: 3. Рассчитаем время t x достижения концентрации С А = 0,01 моль/л: Пример 19. Реакция превращения пара-водорода в орто-водород протекает по следующему механизму (М – инертная частица): Пользуясь методом квазистационарных концентраций, получить выражение для скорости конверсии пара-водорода. Решение. Из уравнения (2) следует, что скорость образования орто-водорода равна: Метод квазистационарных концентраций применяем для активных атомов водорода
Из этого выражения следует, что Заметим, что в реакции (2) число атомов Н не изменяется, поэтому скорость изменения их концентрации определяется первой и третьей реакциями. Таким образом, получаем 163. Для обратимого процесса А В константы скоростей прямой и обратной реакций равны соответственно k 1 = 0,01 c – 1 и k 2 = 0,15 c – 1 . Начальные концентрации веществ А и В взяты равными 0,2 моль/л. Определить концентрации этих веществ через 8 с. 164. Константа равновесия обратимой реакции А В равна 10, а константа скорости прямой реакции равна 0,2 с – 1 . Определить время, за которое концентрации обоих веществ достигнут равенства, если вначале в системе содержалось только вещество А. 165. Для обратимой реакции А В начальные концентрации веществ равны С A0 = = 0,4 моль/л и С В0 = 0. Через 10 мин после начала реакции С A = 0,15 моль/ л и С В = = 0,25 моль/ л. Определить концентрацию вещества А через 20 мин, если константа равновесия реакции равна K = 3. 166. Константа скорости гомогенного мономолекулярного процесса цис-транс-изомеризации бутена при 417 0 С равна 1,6 . 10 6 с – 1 . Константа равновесия при этой температуре равна 1,14. В начальный момент времени в системе присутствует только цис-изомер. Вычислить время достижения равных концентраций изомеров. 📽️ ВидеоХимическое равновесие. Закон действующих масс.Скачать  Скорость химических реакций. 9 класс.Скачать  Порядок реакцииСкачать  Биохимия | Кинетика ферментативных реакций: константа Михаэлиса и график Лайнуивера-БеркаСкачать  Влияние температуры на скорость химических реакций. 10 класс.Скачать  Вычисление константы скорости реакции | Задачник по химии ГлинкаСкачать  Основы химической кинетикиСкачать  Скорость химической реакции. Практическая часть. 10 класс.Скачать  Скорость химической реакцииСкачать  Определение порядка реакции методом подбора кинетического уравненияСкачать  Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 1ч. 10 класс.Скачать  Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать  Химическая кинетика I. Порядок реакции.Скачать  3 1 Константа химической реакцииСкачать  |








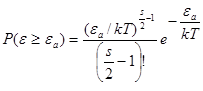










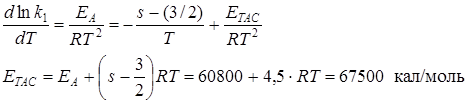
 .
. .
.
 .
. .
. B (k1)
B (k1) 
 A
A .
. ,
, ,
,
 ,
,  ,
,  .
.

 ,
, — концентрация промежуточных частиц. В
— концентрация промежуточных частиц. В .
. .
. ,
, . (*)
. (*) — количество прореагировавшего вещества А к моменту равновесия – равно
— количество прореагировавшего вещества А к моменту равновесия – равно .
. .
. моль/л
моль/л моль/л;
моль/л; ,
, .
.
 .
.
 .
.

 .
. .
. .
. .
.