При равенстве энтальпийного и энтропийного факторов Δ Н = Т Δ S Δ G = 0 , что является термодинамическим условием химического равновесия. Химическое равновесие имеет динамический характер. Скорость реакции (число частиц образующихся в единицу времени в единице объема) в прямом направлении равна скорости реакции в обратном направлении. В этот момент концентрации исходных веществ и продуктов реакции не изменяются во времени и называются равновесными концентрациями. Они обозначаются символом вещества в квадратных скобках.
При равновесии химической реакции:
b B + d D = l L + m M

где p p , L , p pM , p p , D , p pB –равновесные парциальные давления веществ, а [ L ], [ M ],[ D ],[ B ] –равновесные концентрации веществ; l , m , d , b — показатели степени, равные стехиометрическим коэффициентам.
Отношения произведений парциальных давлений или концентраций получили названия констант химического равновесия соответственно К р или К с :
Эти уравнения являются математическими выражениями закона действующих масс, открытого норвежскими учеными К. Гульдбергом и П. Вааге в 1867 г.:
отношение произведения равновесных концентраций продуктов реакции в степенях, равных стехиометрическим коэффициентам, к произведению равновесных концентраций исходных веществ в степенях, равных стехиометрическим коэффициентам, при Т = со nst , является величиной постоянной.
Например, для реакции синтеза аммиака:
закон действующих масс имеет вид:
Подставляя выражение константы в уравнения, получаем
Рассчитав величину Δ G 0 химической реакции, можно определить константу химического равновесия. Используя закон действующих масс, можно рассчитать равновесные концентрации реагирующих веществ.
Из вышеприведенного уравнения следует
Энергия Гиббса процесса имеет значение Δ G 0 = Δ H – T Δ S . Тогда
Если Δ Н и Δ S не зависят от температуры, то производная константы равновесия по температуре будет равна:
Это изобара равновесия. Она показывает, что константа равновесия экзотермической реакции уменьшается, а эндотермической реакции возрастает с повышением температуры. С увеличением абсолютного значения энтальпии реакции и уменьшением температуры чувствительность константы равновесия ( d ( ln K c )/ dT ) к изменению температуры повышается.
При изменении равновесных концентраций исходных веществ и продуктов реакции путем воздействия на систему происходит смещение химического равновесия. Если увеличиваются равновесные концентрации продуктов реакции, то говорят о смещении равновесия вправо. Если при внешнем воздействии увеличиваются концентрации исходных веществ, то говорят о смещении равновесия влево.
Характер смещения равновесия можно прогнозировать, применяя принцип французского ученого Ле Шателье :
если на систему, находящуюся в равновесии, оказывается внешнее воздействие, то равновесие смещается в том направлении, которое ослабляет внешнее воздействие.
Принцип Ле Шателье следует из закона действующих масс. Если система находится при постоянной температуре, то константа равновесия при внешних воздействиях остается постоянной. Поэтому любое изменение равновесных концентраций веществ должно приводить к такому изменению равновесных концентраций других веществ, чтобы соблюдалось постоянство константы равновесия.
Рассмотрим процесс конверсии метана:
Константа равновесия этого процесса имеет вид:
1. Рассмотрим, как влияет изменение концентраций на смещение равновесия. При увеличении концентрации метана СН 4 равновесие системы нарушается, идет прямая реакция. Концентрации продуктов реакции СО 2 и Н2 увеличиваются, а концентрации Н2О уменьшается. Процесс будет протекать до тех пор, пока не установится новое равновесие. Новые равновесные концентрации компонентов будут такими, что константа равновесия не изменится. Если увеличить концентрацию СО 2 , то по принципу Ле Шателье равновесие сместится влево.
2. Если в результате реакции изменяется число молей газообразных веществ, то изменяется общее давление в системе и происходит смещение равновесия. В соответствии с принципом Ле Шателье увеличение общего давления вызывает смещение равновесия в сторону уменьшения числа молей газообразных веществ, т.е. в сторону уменьшения давления. Для рассматриваемой реакции увеличение давления должно смещать равновесие влево (слева- 3 моля, справа – 5 молей).
3. С увеличением температуры равновесие смещается в сторону эндотермических реакций, т.е. реакций протекающих с поглощением теплоты, понижение – в сторону экзотермических реакций.
Итак, принцип Ле Шателье позволяет создавать такие условия протекания реакции, которые обеспечивают максимальный выход продуктов реакции.
Химические реакции, протекающие на границе раздела фаз, называются гетерогенными химическими реакциями.
При равенстве скоростей прямой и обратной реакции наступает химическое равновесие в гетерогенной системе. Примерами гетерогенных процессов является пароводяная конверсия углерода, или восстановление оксидов металлов водородом:
Как и для любого равновесия, условием гетерогенного химического равновесия является равенство энергии Гиббса нулю, Δ G = 0 .
Как и в случае гомогенной химической реакции, константа гетерогенного равновесия равна отношению произведения равновесных концентраций (активностей) или парциальных давлений продуктов реакций к произведению равновесных концентраций (активностей) или парциальных давлений исходных веще ств в ст епенях, равных стехиометрическим коэффициентам в уравнении. Для реакции пароводяной конверсии углерода константа равновесия имеет вид:
для восстановления металла
Из приведенных выражений следует, что в уравнения констант гетерогенного химического равновесия не входят концентрации твердых веществ, участвующих в прямой и обратной реакциях. Это особенность гетерогенного химического равновесия.
Так как прямая и обратная реакции протекают на одной и той же поверхности раздела фаз, то площадь поверхности раздела фаз также не входит в уравнение константы химического равновесия.
Константа гетерогенного химического равновесия зависит от температуры. Она возрастает с увеличением температуры для эндотермической прямой реакции и уменьшается с увеличением температуры в случае экзотермической прямой реакции. Расчеты проводятся по тем же формулам, что и для гомогенных реакций.
Смещение равновесия гетерогенных реакций подчиняется принципу Ле Шателье . При повышении температуры оно смещается в сторону эндотермической реакции. При повышении давления или концентрации исходных веществ равновесие смещается в сторону образования продуктов реакции, при повышении концентрации или давления продуктов реакции равновесие смещается в сторону обратной реакции. При повышении общего давления равновесие сдвигается в направлении уменьшения числа молекул газообразных веществ.
Твердые исходные вещества и продукты реакции не влияют на смещение гетерогенного химического равновесия.
Одно и то же вещество может при изменении температуры и давления переходить в различные агрегатные состояния. Эти переходы, осуществляемые без изменения химического состава, называются фазовыми переходами. Если рассматривается гетерогенная система, в которой нет химического воздействия, а имеются лишь фазовые переходы, то при постоянстве температуры и давления существует так называемое фазовое равновесие. Примерами фазового равновесия могут быть процессы плавления, кристаллизации, испарения, конденсации воды. Это равновесие характеризуется некоторым числом фаз, компонентов и числом степеней термодинамической свободы системы или числом степеней свободы.
Фаза – это однородная часть системы одинаковая по составу и свойствам, имеющая поверхность раздела, и которая может быть выделена из системы чисто механическим путем.
Так, система лед+вода имеет две фазы.
Компонентом называется химически однородная составная часть системы, которая может быть выделена из системы и может существовать вне ее .
Так, в растворе хлорида натрия компонентами являются вода и хлорид натрия, но ионы натрия и хлора не могут считаться компонентами.
Число степеней свободы определяется как число параметров системы (температура, давление), которые могут быть произвольно изменены в некоторых пределах без изменения числа и природы фаз в системе.
У системы, состоящей лишь из газа, можно менять два параметра, третий система устанавливает произвольно сама.
Число степеней свободы определяется правилом фаз Дж .Г иббса (1876 г.):
число степеней свободы равновесной системы, на которую влияют только температура и давление, равно числу независимых компонентов системы минус число фаз плюс два:
где С – число степеней свободы; К – число компонентов; Ф – число фаз; 2 – число независимых параметров, например температура и давление.
Классификацию систем можно проводить: по числу фаз (однофазные, двухфазные и т.д.); по числу компонентов системы (однокомпонентные, двухкомпонентные и т.д.); по числу степеней свободы – инвариантные (С = 0), моновариантные (С = 1), дивариантные (С = 2) и т. д. Диаграммы, по которым можно определить условия устойчивости фаз и фазового равновесия, называются фазовыми диаграммами или диаграммами состояния. Для однокомпонентных систем правило фаз имеет вид
Примером однокомпонентной системы служит диаграмма состояния воды в координатах давление – температура . 
Кривая ОВ – это кривая плавления. При увеличении давления температура плавления немного уменьшается, что обусловлено разрывом водородных связей при повышении давления.
Кривая ОА отражает процесс сублимации, т.е. перехода из твердого состояния в газообразное , минуя жидкое. Кривая ОД описывает поведение воды в неустойчивом (метастабильном) состоянии. Явление образования метастабильного состояния получило название переохлаждения.
В точке О существует равновесие одновременно между тремя фазами. Она называется тройной точкой воды, и для нее давление равно 610 Па и температура 273,15 К.
Процесс поглощения одного вещества поверхностью или объемом другого называется сорбцией.
Вещество, частицы которого поглощаются (газ, жидкость или растворенный компонент), называют сорбатом , а поглотитель (чаще твердое тело) – сорбентом .
Сорбционные процессы играют большую роль в технике. Например, для поддержания высокого вакуума в действующем электровакуумном приборе применяют геттеры – специально изготовленные материалы, которые активно поглощают остаточные газы. В качестве геттеров используют компактные ( Zr , Ta , Nb и др.) или распыленные ( Ba , Ca , Sr ) металлы. Сорбционные процессы широко используют в металлургии при обогащении руд (флотация), в энергетике при водоподготовке (ионный обмен) и др.
При контакте сорбент поглощает сорбат поверхностью или объемом. Сорбция только поверхностью называется адсорбцией , а только объемом – абсорбцией . Процесс обратный адсорбции называется десорбцией.
Адсорбция связана с особым энергетическим состоянием частиц на поверхности адсорбента в отличие от энергетического состояния частиц в его объеме . Частицы во внутренних слоях вещества испытывают одинаковое притяжение со стороны окружающих частиц по всем направлениям.
Частицы же поверхностного слоя подвергаются неодинаковому притяжению со стороны внутренних слоев вещества и со стороны частиц граничащей с веществом посторонней фазы. Поэтому частицы поверхностного слоя адсорбента обладают свободной поверхностной энергией , которая может быть снижена за счет возникновения абсорбционных взаимодействий с молекулами, атомами и ионами адсорбата .
Для границы раздела фаз жидкость – газ (пар) обычно используют термин «удельная (на 1 м 2 ) поверхностная энергия», называемая поверхностным натяжением , которая равно работе образования единицы площади поверхности раздела фаз (Дж/м 2 ).
Поверхностная энергия – это энергия Гиббса Δ G образования поверхности. Она равна произведению удельной поверхностной энергии σ на площадь поверхности раздела фаз S :
Удельная поверхностная энергия зависит от природы вещества. Чем выше энергия взаимодействия между частицами вещества, тем выше удельная поверхностная энергия. С увеличением температуры удельная поверхностная энергия уменьшается.
В зависимости от природы сил взаимодействия адсорбирующего вещества с адсорбентом различают физическую и химическую (хемосорбцию) адсорбцию. В первом случае при адсорбции возникают вандерваальсовы взаимодействия, во втором – химические связи.
Физическая адсорбция характеризуется невысоким тепловым эффектом и обратимостью.
Хемосорбция протекает необратимо. Тепловой эффект ее близок к тепловому эффекту химических реакций.
Поскольку адсорбция протекает самопроизвольно, то энергия Гиббса имеет отрицательное значение
Тепловой эффект адсорбции имеет также отрицательное значение
Если адсорбция протекает из газовой, жидкой фазы на поверхность жидкой или твердой фазы, то в процессе адсорбции происходит упорядочение адсорбированных частиц и энтропия системы уменьшается, т.е.
Отсюда следует, что с увеличением температуры энергия Гиббса системы возрастает, и при некоторой температуре Т р наступает равновесие, в это время скорость адсорбции равна скорости десорбции. При этом
При увеличении температуры адсорбция уменьшается. То есть вещество можно адсорбировать при невысокой температуре и десорбировать при более высокой.
Абсорбционное равновесие подвижно и может быть смещено в ту или иную сторону в соответствии с принципом Ле Шателье .
Количественно адсорбцию можно выражать в молях адсорбата на единицу площади адсорбента, моль/м 2 . Адсорбция зависит от природы адсорбента и адсорбата , температуры и концентрации или давления адсорбата . Кривую зависимости величины адсорбции Г от равновесных концентраций С или давлений р адсорбата при постоянной температуре Т называют изотермой адсорбции :
Г = f ( C ) или Г = f ( p ) при Т = const .
Изотерма адсорбции на однородной поверхности адсорбента была выведена американским ученым Дж .Л энгмюром . При выводе уравнения было сделано предположение, что поверхность адсорбента однородна и при максимальном заполнении образуется мономолекулярный слой. В этом случае уравнение имеет вид:
где Г ∞ — адсорбция при максимальном заполнении;
с – равновесная концентрация адсорбата ;
р – равновесное давление адсорбата ;
К а – константа равновесия процесса адсорбции.

Изотерма Лэнгмюра редко соблюдается в реальности, поэтому предложены другие уравнения.
В 1906 г. Фрейндлих предложил эмпирическое уравнение изотермы. Уравнение Фрейндлиха имеет вид:
где К ф и n – постоянные.
При адсорбции изменяются свойства поверхностного слоя, т.е. поверхностное натяжение. Адсорбирующиеся вещества могут понижать поверхностное натяжение (это поверхностно — активные вещества – ПАВ), повышать поверхностное натяжение (поверхностно — инактивные вещества) и не влиять на поверхностное натяжение (поверхностно — неактивные вещества).
Широкое применение нашли лишь ПАВ. Способностью уменьшать поверхностное натяжение, т.е. поверхностной активностью обладают молекулы вещества, имеющие неполярные гидрофобные углеводородные части («хвосты») и полярные гидрофильные группы («головы»). К полярным принадлежат группы
К ПАВ принадлежит натриевая соль стеариновой кислоты, входящей в состав мыла
Поверхностная активность обусловлена гидрофобной частью молекул ПАВ («хвостами»), которые выталкиваются из полярного растворителя, в то время как гидрофильные группы («головы») удерживают молекулы ПАВ на границе раздела фаз. Таким образом, молекулы ПАВ адсорбируются на границе раздела фаз, причем гидрофобная их часть обращена в сторону газа или неполярной жидкости, гидрофильная часть – в сторону полярной жидкости или твердого гидрофильного адсорбента.
Концентрация ПАВ в поверхностном слое на несколько порядков выше, чем в объеме жидкости, поэтому даже при малом содержании ПАВ они значительно снижают поверхностное натяжение. Поверхностная активность ПАВ возрастает с увеличением длины углеводородной части молекул и их концентрации.
Изменение поверхностного натяжения под действием ПАВ влияет на смачиваемость твердых тел жидкостью. Этот эффект используется для очистки тканей (стирка, чистка) или металлов от жировых загрязнений применением ПАВ, при адсорбции которых на границе раздела фаз вода – жир, вода – твердое тело изменяется поверхностное натяжение воды на этих границах, что приводит к переходу жира в виде капель в водную среду.
Применение ПАВ позволяет разделять пустую породу и руду при флотации руд. Пустая порода смачивается водой, содержащей ПАВ, а руда поднимается вверх с пузырьками воздуха, продуваемого через раздробленную породу в воде.
- Химическое равновесие. Принцип Ле Шателье
- Понятие химического равновесия
- Признаки химического равновесия
- Принцип Ле Шателье
- Влияние температуры на химическое равновесие
- Влияние давления на химическое равновесие
- Влияние концентрации на химическое равновесие
- Константа химического равновесия
- Примеры решения задач
- Задачи для самостоятельного решения
- Уравнение константы равновесия гетерогенной химической реакции sio2 2h2
- 🔍 Видео
Видео:Обратимость и необратимость химических реакций. Химическое равновесие. 1 часть. 9 класс.Скачать

Химическое равновесие. Принцип Ле Шателье
Материалы портала onx.distant.ru
Понятие химического равновесия
Признаки химического равновесия
Принцип Ле Шателье
Влияние температуры на химическое равновесие
Влияние давления на химическое равновесие
Влияние концентрации на химическое равновесие
Константа химического равновесия
Примеры решения задач
Задачи для самостоятельного решения
Видео:Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 1ч. 10 класс.Скачать

Понятие химического равновесия
Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.
Видео:Химическое равновесие. Константа равновесия. 10 класс.Скачать

Признаки химического равновесия
- Состояние системы остается неизменным во времени при сохранении внешних условий.
- Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
- Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
- К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
- В состоянии равновесия энергия Гиббса достигает своего минимального значения.
Видео:Химическое равновесие. 10 класс.Скачать

Принцип Ле Шателье
Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия):
Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.
Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.
Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:
Видео:Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 3ч. 10 классСкачать

Влияние температуры на химическое равновесие
При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.
Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.
В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.
Видео:Химическое равновесиеСкачать

Влияние давления на химическое равновесие
Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.
В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO2. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.
Видео:Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 4ч. 10 класс.Скачать

Влияние концентрации на химическое равновесие
Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O2 вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO2. Увеличение концентрации NO2 смещает равновесие в сторону исходных веществ.
Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.
При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.
Видео:Химическое равновесие. Закон действующих масс.Скачать

Константа химического равновесия
Для химической реакции:
константа химической реакции Кс есть отношение:
В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.
Константа химического равновесия связана с изменением энергии Гиббса уравнением:
ΔGT о = – RTlnK (2)
Видео:Химическое равновесие. Константа равновесия. Обратимость реакций.Скачать

Примеры решения задач
Задача 1. При некоторой температуре равновесные концентрации в системе 2CO (г) + O2 (г)→2CO2 (г) составляли: [CO] = 0,2 моль/л, [O2] = 0,32 моль/л, [CO2] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O2, если исходная смесь не содержала СО2.
Решение.
Вещество
Во второй строке под Спрореагир понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO2, причем, Сисходн= Спрореагир + Сравн.
Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса
Решение.
ΔG298 о = 2·(- 16,71) кДж = -33,42·10 3 Дж.
lnK = 33,42·10 3 /(8,314× 298) = 13,489. K = 7,21× 10 5 .
Задача 3. Определите равновесную концентрацию HI в системе
если при некоторой температуре константа равновесия равна 4, а исходные концентрации H2 , I2 и HI равны, соответственно, 1, 2 и 0 моль/л.
Решение. Пусть к некоторому моменту времени прореагировало x моль/л H2.
| Вещество | H2 | I2 | HI |
| сисходн., моль/л | 1 | 2 | 0 |
| спрореагир., моль/л | x | x | 2x |
| cравн., моль/л | 1-x | 2-x | 2x |
Тогда, К = (2х) 2 /((1-х)(2-х))
Решая это уравнение, получаем x = 0,67.
Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.
Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H2(г) + HCOH(г) →CH3OH(г) становится равной 1. Принять, что ΔН о Т » ΔН о 298, а ΔS о T » ΔS о 298.
Решение.
Если К = 1, то ΔG о T = — RTlnK = 0;
ΔН о 298 = -202 – (- 115,9) = -86,1 кДж = — 86,1× 10 3 Дж;
ΔS о 298 = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;
0 = — 86100 — Т·(-109,52)
Задача 5. Для реакции SO2(Г) + Cl2(Г) →SO2Cl2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO2Cl2, если исходные концентрации SO2, Cl2 и SO2Cl2 равны 2, 2 и 1 моль/л соответственно.
Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO2.
| Вещество | SO2 | Cl2 | SO2Cl2 |
| cисходн., моль/л | 2 | 2 | 1 |
| cпрореагир., моль/л | x | x | х |
| cравн., моль/л | 2-x | 2-x | x + 1 |
Решая это уравнение, находим: x1 = 3 и x2 = 1,25. Но x1 = 3 не удовлетворяет условию задачи.
Следовательно, [SO2Cl2] = 1,25 + 1 = 2,25 моль/л.
Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Задачи для самостоятельного решения
1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.
Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества
газообразных веществ, то равновесие сместится вправо в реакции 3.
2. При некоторой температуре равновесные концентрации в системе:
составляли: [HBr] = 0,3 моль/л, [H2] = 0,6 моль/л, [Br2] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.
К = 4; исходная концентрация HBr составляет 1,5 моль/л.
3. Для реакции H2(г) + S(г) →H2S(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H2 и S, если исходные концентрации H2, S и H2S равны, соответственно, 2, 3 и 0 моль/л.
[H2] = 0,5 моль/л; [S] = 1,5 моль/л.
4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса
становится равной 1. Примите, что ΔН о Т≈ΔН о 298, а ΔS о T≈ΔS о 298
5. Используя справочные данные, рассчитайте константу равновесия процесса:
6. Для реакции 2С3Н8(г) → н-С5Н12(г)+СН4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.
7. При температуре 500 К константа равновесия процесса:
равна 3,4·10 -5 . Вычислите Δ G о 500.
8. При температуре 800 К константа равновесия процесса н-С6Н14(г)+ 2С3Н6(г)+Н2(г) равна 8,71. Определите ΔG о f,800(С3Н6(г)), если ΔG о f,800(н-С6Н14(г)) = 305,77 кДж/моль.
9. Для реакции СО(г) + Cl2(г) →СO2Cl2(г) при некоторой температуре равновесная концентрация СO2Cl2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО(г) и Cl2(г) равны соответственно 2,0 и 1,8 моль/л.
10. При некоторой температуре равновесные концентрации в системе 2SО2(г) + О2(г) →2SO3(г) составляли: [SО2 ]=0,10 моль/л, [О2]=0,16 моль/л, [SО3]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО2 и О2.
К=4,0; исходная концентрация SО2 составляет 0,18 моль/л;
исходная концентрация О2 составляет 0,20 моль/л.
Видео:Гетерогенное равновесиеСкачать

Уравнение константы равновесия гетерогенной химической реакции sio2 2h2
§ 4. Равновесие в гетерогенных системах
Системы, в состав которых входит более одной фазы, называются гетерогенными. Они могут содержать газовую фазу, а также конденсированные фазы — твердые или жидкие. Рассмотрим случай, когда все участвующие в реакции конденсированные фазы представляют собой вещества, которые не образуют друг с другом растворов, и, таким образом, только газовая фаза может быть раствором. К числу таких реакций относятся, например, следующие:
В общем виде для гетерогенной реакции Aг + Вк = Dк + 2Eг (индекс «к» означает конденсированную фазу) условие равновесия при постоянных температуре и давлении состоит в равенстве нулю алгебраической суммы свободных энергий Гиббса всех участвующих в реакции веществ: ΔG = Gd + 2 Gе — Ga — Gb.
Энергия Гиббса моля (идеального) газа определяется уравнением (II.28),
Уравнение состояния идеальных газов применимо лишь в том случае, если можно пренебречь собственным объемом молекул газа. Поэтому при использовании законов идеальных газов для расчетов гетерогенных равновесий можно пренебречь объемом конденсированных фаз ввиду его малости. Отсюда на основании уравнения (II.33) следует, что энергия Гиббса веществ, находящихся в твердом или жидком состоянии, практически не зависит от давления 1 . Таким образом, для рассматриваемой реакции:
G
| 0 |
| d |
+ 2G
| 0 |
| e |
+ 2RT ln pe — G
| 0 |
| a |
— RT ln pa — G
| 0 |
| b |
= 0.
Перенося в одну часть уравнения величины, зависящие только от температуры, а в другую — от давления, получим:

Правая часть этого уравнения, обозначаемая ψ(T), при T = const величина постоянная и, следовательно, отношение p
| 2 |
| e |
/ p
| 2 |
| a |
при этом условии также постоянно. Это означает, что выражение закона действующих масс для гетерогенных
систем остается таким же, как и для гомогенных систем, но только парциальные давления (или концентрации) конденсированных фаз не входят в уравнение константы равновесия.
над смесью карбида железа и металлического железа отношение парциального давления метана к квадрату парциального давления водорода при равновесии есть величина постоянная, зависящая от температуры, т.е. Kp = pCH1 / р
| 2 |
| H2 |
.
Для реакции, происходящей при обжиге известняка:
Это означает, что каждой температуре соответствует строго определенное равновесное давление углекислого газа над смесью СаСО3 и СаО. Это давление часто называют упругостью диссоциации соответствующего соединения. Так как реакция диссоциации эндотермична, то с ростом температуры pCO2, увеличивается.
Как и в случае гомогенных реакций, по значению константы равновесия для гетерогенных реакций можно рассчитать их выход.
Так, выход реакции восстановления FeO оксидом углерода, взятым при нормальном атмосферном давлении,
определяется следующим образом.
При равновесии давление СО2 будет х, а СО (1 — х), откуда
Следует лишь отметить, что этот расчет носит несколько приближенный характер, так как при высоких температурах FeO имеет хотя и небольшую, но измеримую растворимость в твердом железе.
Изменение свободной энергии Гиббса при рассмотренной выше гетерогенной реакции Aг + Вк составляет:
ΔG = ψ(T) + RT ln (p
| 2 |
| e |
/ pa).
Для определения величины функции ψ(T) рассмотрим равновесное состояние. В этом случае ΔG = 0, a p
| 2 |
| e |
/ pa = Kp, откуда находим, что ψ(T) = — RT ln Kp, и, следовательно:
ΔG = —RT ln Kp + RT ln (p
| 2 |
| e |
/ pa) (III.23)
Таким образом, изменение энергии Гиббса при гетерогенных реакциях определяется таким же уравнением, как и для газовых реакций.
В специальном случае, если все участвующие в реакции вещества взяты в стандартных состояниях, ΔG = —RT ln Kp.
Вывод уравнения (III.19) для зависимости Кp от температуры применим и в рассматриваемом случае, так что зависимость константы равновесия гетерогенных реакций от температуры определяется тем же уравнением, что и для газовых реакций: dlnKp/dT = ΔH 0 /RT 2 .
Константы равновесия ряда реакций не могут быть экспериментально определены из-за весьма малых величин парциальных давлений (или концентраций) некоторых из компонентов. Однако их можно вычислить при помощи принципа комбинирования равновесий, аналогично описанному в гл. I способу определения теплот реакций при помощи закона Гесса.
Пусть, например, требуется определить Кp реакции FeOт = Feт + 1/2О2г, равную рO
| 1/2 |
| 2 |
, значение которой даже при высоких температурах столь мало, что не поддается прямому измерению. Равновесия же реакций
измеримы. Они характеризуются константами:
К
| ’ |
| р |
= pH2O/pH2 и ΔG
| 0 |
| 2 |
= — RT ln K
| ’’ |
| p |
Если эти две реакции протекают одновременно в одном объеме и при одной температуре, то установившиеся при равновесии величины рH2 и рH2O должны соответствовать как значению К
| ’’ |
| p |
, так и К
| ’ |
| p |
. Отсюда следует, что К
| ’ |
| p |
К
| ’’ |
| p |
= p
| 1/2 |
| O2 |
. Такой же результат может быть получен суммированием стандартных изменений энергий Гиббса двух последних реакций:
ΔG
| 0 |
| 1 |
= —RT ln К’р и ΔG
| 0 |
| 2 |
= —RT ln Кp.
Это обусловлено тем, что G есть функция состояния и ее изменение не зависит от пути процесса. Поэтому
ΔG 0 = —RT ln p
| 1/2 |
| pO2 |
= ΔG
| 0 |
| 1 |
+ ΔG
| 0 |
| 2 |
.
Рассмотрим некоторые примеры расчетов гетерогенных равновесий.
Пусть требуется определить наиболее низкую температуру, при которой может эффективно проводиться обжиг известняка с целью получения извести. Очевидно, этот
процесс пойдет с достаточной скоростью при условии, что давление углекислого газа будет не меньше атмосферного. Найдем температуру, при которой упругость диссоциации равна 1 атм.
Из таблицы стандартных величин для СаСО3, СаО и СО2 соответственно находим Δ
| 0 |
| 298 |
: — 1206,66; -635,55 и -393,51 кДж/моль и S
| 0 |
| 298 |
: 92,88; 39,75; 213,80 Дж/(моль·К). Отсюда ΔH
| 0 |
| 298 |
= 177,61 кДж/моль и ΔS
| 0 |
| 298 |
= 160,66 Дж/(моль·К).
Принимая, что для этой реакции ΔCp = 0, найдем зависимость изменения энергии Гиббса от температуры: ΔG
| 0 |
| T |
= 177610 — T·160,66. Очевидно, что рCO2 = Kp = 1 при ΔG
| 0 |
| T |
= 0. Это достигается при Т = 177610/160,66 − ∼ 1100 К. Более точный расчет с использованием величин теплоемкостей приводит к более высокой температуре (1153 К).
Рассчитаем выход реакции восстановления FeO в твердом состоянии СО при относительно низкой температуре 873 К: FeOт + COг = Feт + COг = Feт + CO2г.
Из таблиц стандартных величин для FeO, CO, Fe и СО2 соответственно находим ΔH
| 0 |
| 298 |
: -266,52; -110,46; 0,0; 393,51 кДж/моль ΔS
| 0 |
| 298 |
: 53,97; 197,9; 27,15 и 213,8 Дж/(моль·К).
Для реакции ΔH
| 0 |
| 298 |
= -16,53 кДж/моль и ΔS
| 0 |
| 298 |
= -10,92 Дж/(моль·К). Отсюда для реакции в предположении, что ΔCp = 0, найдем ΔG
| 0 |
| T |
= -16530-Т(-10,92). При 600° C (873 К) Δ
| 0 |
| 873 |
= -16530 + 873·10,92 = -6997 = -19,14·873 lg Кp и Кр = 2,6.
Если исходное давление СО составляет единицу, то выход х, рассчитанный по уравнению Кp = х/(1 — х), составляет около 0,72 или 72 %.
Содержащаяся в стали сера является вредной примесью. Она образует с железом химическое соединение FeS.
Выясним возможность удаления включений FeS из стали с помощью водорода при приемлемой температуре, например 1000 К, по реакции: FеSт + Н2г = Fет + Н2Sг
Из таблиц стандартных величин для GeO, CO, Fe и CO2 соответственно находим Δ: 94,98; 0,0; 0,0; 20,1 кДж/моль; ΔS
| 0 |
| 298 |
: 67,4; 134,8; 27,1 и 205,4 Дж/(моль·К). Для реакции ΔH
| 0 |
| 298 |
= 74,9 кДж/моль, ΔS
| 0 |
| 298 |
= 30,5 Дж/моль·К. Отсюда (приближенно принимая ΔCp = 0) при 1000 К:
ΔG
| 0 |
| 1000 |
= 74900 — 1000·30,5 = 44400 = -19,14·1000 lg Kp и Kp = pH2S/pH2 = 4,8·10 -3 .,
т.е. в равновесной газовой смеси парциальное давление сероводорода примерно в 200 раз меньше парциального давления водорода. Очевидно, для существенного удаления серы из металла в таких условиях необходимы весьма большие объемы водорода.
В природе и в технике встречаются реакции, проходящие только в конденсированных фазах между чистыми веществами при полном отсутствии в системе газов и растворов.
Для таких реакций, подобных фазовым превращениям, условия равновесия не могут описываться законом действующих масс, так как в них не участвуют газы и при их протекании не изменяется состав конденсированных фаз. Поэтому в подобных случаях бессмысленно использовать константу равновесия для установления направления реакции. При данной температуре в таких системах будут устойчивы либо исходные вещества, либо продукты реакции в зависимости от значений энергий Гиббса. Сосуществовать все участники реакции могут лишь при одной температуре, когда ΔG = 0. Выше этой температуры реакция идет до конца в одном направлении, а ниже — до конца в противоположном. В качестве примера рассмотрим вопрос об условиях превращения графита в алмаз.
Из таблиц стандартных величин следует, что для графита и алмаза соответственно ΔH
| 0 |
| 298 |
: 0,0 и 1895 Дж/моль и S
| 0 |
| 295 |
: 5,694 и 2,439 Дж/(моль·К). Таким образом, для процесса превращения ΔH
| 0 |
| 298 |
= 1895 Дж/моль и ΔS
| 0 |
| 298 |
= -3,255 Дж/(моль·К).
Если в первом приближении допустить, что ΔCp = 0 (ΔH 0 и ΔG
| 0 |
| 298 |
не зависят от температуры), то Δ
| 0 |
| T |
= 1895 + 3,255 Т и ΔG
| 0 |
| 298 |
= 2863 Дж/моль. Таким образом, изменение энергии Гиббса процесса при любой температуре положительно, т.е. устойчивой фазой всегда будет графит, и его превращение в алмаз невозможно. Однако в этом расчете принималось во внимание влияние на энергию Гиббса только одного параметра — температуры. Между тем на эту функцию влияет также и изменение давления, так как согласно уравнению (II.33) (∂G/∂p)т = V.
Если энергия Гиббса графита с возрастанием давления будет увеличиваться быстрее, чем алмаза, то при высоких давлениях величина ΔG может стать отрицательной. Это действительно имеет место, так как мольный объем графита больше, чем мольный объем алмаза.
Зная плотности графита (2,25 г/см 3 ) и алмаза (3,51 г/см 3 ), можно вычислить, при каком давлении возможно превращение графита в алмаз при комнатной температуре. Очевидно, для этого убыль энергии Гиббса, обусловленная повышением давления, должна быть по абсолютной
величине, по крайней мере, не меньше 2863 Дж/моль. Зависимость ΔG превращения от давления определяется уравнением:
Так как плотность практически не зависит от давления, то после интегрирования приведенного выше уравнения получаем:
Левая часть последнего уравнения, представляющая собой убыль энергии Гиббса вследствие увеличения давления сверх нормального атмосферного, выражена в джоулях, а правая в см 3 ·атм. Учитывая, что один джоуль эквивалентен 9,8·10 5 см 3 Па и нормальное атмосферное давление составляет около 10 5 Па, найдем давление, теоретически необходимое для превращения графита в алмаз, по уравнению:
ΔG298 = 2283 = —
| 1,91(p — 10 5 ) |
| 9,8·10 5 |
.
Отсюда р − ∼ 14700·10 5 Па или ∼ 14700 атм.
Таким образом, превращение графита в алмаз при комнатной температуре термодинамически возможно при давлении, несколько превышающем 14700·10 5 Па. Однако вследствие очень малой подвижности атомов при комнатной температуре скорость превращения ничтожно мала и на практике его осуществляют, как уже отмечалось, при высоких температурах и давлениях.
Приведенные примеры расчетов показывают, что термодинамика позволяет предвидеть принципиальную возможность или невозможность осуществления разнообразных процессов. Если какой-либо процесс термодинамически возможен, то для его практического проведения необходимо выяснить, при каких условиях он происходит с достаточной скоростью, т.е. целесообразно исследовать его кинетику и провести подбор катализатора, ускоряющего реакцию. Естественно, что если реакция термодинамически невозможна, то применение любого катализатора не позволит ее осуществить.
🔍 Видео
Обратимость и необратимость химических реакций. Химическое равновесие. 2 часть. 9 класс.Скачать

Задача химическое равновесие. РАВНОВЕСНЫЕ КОНЦЕНТРАЦИИ и Кр.Скачать

Условия смещения химического равновесия. 9 класс.Скачать

Химическая кинетика. Скорость химической реакции | ХимияСкачать

Задания на константу равновесия по учебнику ЕреминаСкачать
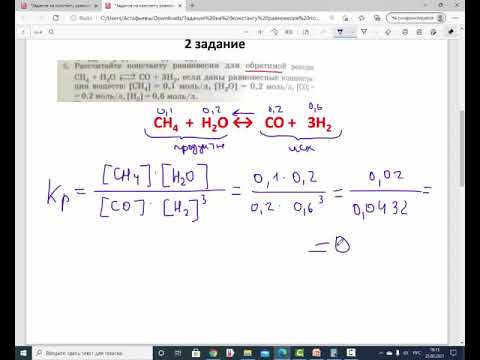
Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 2ч. 10 класс.Скачать

Интуитивное понимание формулы константы равновесия (не обязательно для продолжения курса)Скачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Экзо- и эндотермические реакции. Тепловой эффект химических реакций. 8 класс.Скачать








