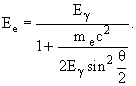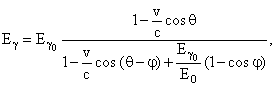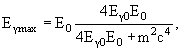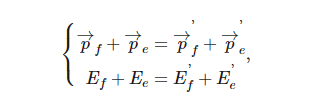Уравнение комптона для угла рассеяния (3 видео)

Уравнение комптона для угла рассеяния

Содержание

Эффект Комптона Compton effect
Обратный комптон-эффект
Эффект Комптона
Объяснение эффекта с помощью квантовых представлений
Почему длина части волн не изменяется?
Эффект Комптона простыми словами: что это такое, формулы
Простое объяснение эффекта Комптона
Формулы для расчета энергии и импульса фотона
Формулы для расчета импульса и энергии релятивистских частиц
Два случая комптоновского рассеяния
📸 Видео

Эффект Комптона
_{Compton effect}

ЭффектКомптона – рассеяние электромагнитного излучения на свободном электроне, сопровождающееся уменьшением частоты излучения (открыт А. Комптоном в 1923 г.). В этом процессе электромагнитное излучение ведёт себя как поток отдельных частиц – корпускул (которыми в данном случае являются кванты электромагнитного поля — фотоны), что доказывает двойственную – корпускулярно-волновую – природу электромагнитного излучения. С точки зрения классической электродинамики рассеяние излучения с изменением частоты невозможно.
Комптоновское рассеяние – это рассеяние на свободном электроне отдельного фотона с энергией λ (h – постоянная Планка, ν – частота электромагнитной волны, λ – её длина, с – скорость света) и импульсом р = Е/с. Рассеиваясь на покоящемся электроне, фотон передаёт ему часть своей энергии и импульса и меняет направление своего движения. Электрон в результате рассеяния начинает двигаться. Фотон после рассеяния будет иметь энергию (и частоту) меньшую, чем его энергия (и частота) до рассеяния. Соответственно после рассеяния длина волны фотона увеличится. Из законов сохранения энергии и импульса следует, что длина волны фотона после рассеяния увеличится на величину

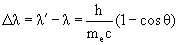
где θ – угол рассеяния фотона, а m_e – масса электрона h/m_ec = 0.024 Å называется комптоновской длиной волны электрона.
Изменение длины волны при комптоновском рассеянии не зависит от λ и определяется лишь углом θ рассеяния γ-кванта. Кинетическая энергия электрона определяется соотношением

Эффективное сечение рассеяния γ-кванта на электроне не зависит от характеристик вещества поглотителя. Эффективное сечение этого же процесса, рассчитанное на один атом, пропорционально атомному номеру (или числу электронов в атоме) Z.
Сечение комптоновского рассеяния убывает с ростом энергии γ-кванта: σ_k

Обратный комптон-эффект

Если электрон, на котором рассеивается фотон, является ультрарелятивистским Ee >> E_γ, то при таком столкновении электрон теряет энергию, а фотон приобретает энергию. Такой процесс рассеяния используется для получения моноэнергетических пучков γ-квантов высокой энергии. С этой целью поток фотонов от лазера рассеивают на большие углы на пучке ускоренных электронов высокой энергии, выведенных из ускорителя. Такой источник γ-квантов высокой энергии и плотности называется Laser-Electron-Gamma-Source (LEGS). В работающем в настоящее время источнике LEGS лазерное излучение с длиной волны 351.1 мкм (

0.6 эВ) в результате рассеяния на электронах, ускоренных до энергий 3 ГэВ, превращается в поток γ-квантов с энергиями 400 МэВ).
Энергия рассеянного фотона E_γ зависит от скорости v ускоренного пучка электронов, энергии E_γ0 и угла столкновения θ фотонов лазерного излучения с пучком электронов, угла между φ направлениями движения первичного и рассеянного фотона

При «лобовом» столкновении

E₀ − полная энергия электрона до взаимодействия, mc 2 − энергия покоя электрона.
Если направление скоростей начальных фотонов изотропно, то средняя энергия рассеянных фотонов _γ определяется соотношением

_γ = (4E_γ/3)·(E_e/mc 2 ).

При рассеянии релятивистских электронов на микроволновом реликтовом излучении образуется изотропное рентгеновское космическое излучение с энергией
E_γ = 50–100 кэВ.
Эксперимент подтвердил предсказанное изменение длины волны фотона, что свидетельствовало в пользу корпускулярного представления о механизме эффекта Комптона. Эффект Комптона наряду с фотоэффектом явился убедительным доказательством правильности исходных положений квантовой теории о корпускулярно-волновой природе частиц микромира.

П o дробнее об обратном комптон-эффекте см. Источники гамма-излучения

Видео:93. Эффект КомптонаСкачать

Эффект Комптона

Как мы знаем, Альберт Эйнштейн в 1905 году предложил для объяснения фотоэффекта так называемую концепцию фотонов. Позже, в 1922 г., американский физик А.Комптон провел серию опытов и подтвердил ее экспериментально. Он провел исследования упругого рассеяния коротковолнового рентгеновского излучения на свободных электронах вещества (или электронах, слабо связанных с атомами) и открыл, что длина волны рассеянного изучения не соответствует ранее принятой волновой теории. Согласно ей, электроны, испытывающие воздействие периодического поля световой волны, совершают вынужденные колебания на частоте волны и поэтому излучают рассеянные волны той же частоты, следовательно, длина волны излучения при рассеянии не должна меняться.

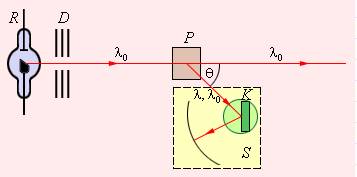
На иллюстрации представлена схема прохождения монохроматического рентгеновского излучения с длиной волны λ 0 , которое исходит из трубки R , через свинцовую диафрагму. После прохождения его направляют узким пучком на слой рассеивающего вещества (алюминия, графита). Затем получившееся излучение, рассеянное под углом θ , анализируют при помощи спектрографа рентгеновских лучей S с дифракционной решеткой в виде кристалла K , помещенного на поворотный столик. Результаты опыта показывают, что в рассеянном излучении длина волны Δ λ увеличивается в зависимости от угла рассеяния.

∆ λ = λ — λ 0 = 2 Λ sin 2 θ 2 .

Здесь параметр Λ = 2 , 43 · 10 – 3 н м выражает так называемую комптоновскую длину волны, которая не имеет связи с свойствами рассеивающего вещества.

Если излучение является рассеянным, то в нем помимо спектральной линии с длиной волны λ присутствует и несмещенная линия, длина волны которой равна λ 0 .

Соотношение интенсивности обеих линий связано с тем, какое вещество использовано в качестве рассеивающего.

Рисунок 5 . 3 . 1 . Эксперимент Комптона (схематическое изображение).

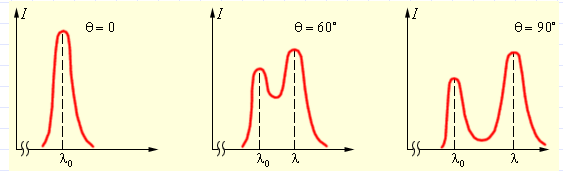
Следующие иллюстрации показывают, как распределяется интенсивность в спектре рассеянного излучения в зависимости от угла рассеивания.

Рисунок 5 . 3 . 2 . Распределение интенсивности в рассеянном излучении.

Видео:АТОМНАЯ ФИЗИКА: Эффект Комптона за 5 минутСкачать

Объяснение эффекта с помощью квантовых представлений

Эффект Комптона был объяснен в 1923 году самим Комптоном и П. Дебаем, которые работали независимо друг от друга. В обоих случаях в основе объяснения лежат квантовые представления.

Если излучение является потоком фотонов, то эффект Комптона происходит из-за упругого столкновения свободных электронов вещества с рентгеновскими фотонами. Рассеивающие вещества имеют слабую связь между ядрами атомов и электронами, поэтому можно считать, что они имеют в составе свободные электроны. При столкновении им передается часть энергии фотонов и часть импульса.

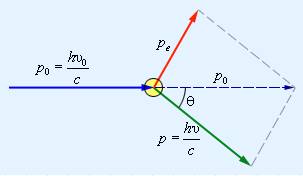
Рассмотрим подробнее процесс упругого столкновения налетающего фотона с импульсом p 0 = h ν 0 c и энергией E 0 = h ν 0 с электроном, у которого энергия покоя составляет E e 0 = m c 2 . После того, как частицы столкнутся, направление движения фотона изменяется, т.е. происходит рассеяние, после чего импульс фотона становится равен p = h ν c , а энергия – E = h ν E 0 . Что касается электрона, то, согласно релятивистской формуле, его энергия становится равной E e = p e 2 c 2 + m 2 c 4 (буквой p e обозначен приобретенный импульс). Запишем формулу закона сохранения:

E + E e 0 = E + E e .

Иначе говоря, h υ 0 + m c 2 = h υ + p e 2 c 2 + m 2 c 4 .

Также нам понадобится закон сохранения импульса:

С помощью теоремы косинусов мы можем перевести его в скалярную форму:

p e 2 = h υ 0 c 2 + h υ c 2 — 2 h 2 c 2 υ 0 υ cos θ .

Рисунок 5 . 3 . 3 . Распределение импульсов при столкновении налетающего фотона и покоящегося электрона

Теперь возьмем эти два соотношения (законы сохранения импульса и энергии), проведем несложные преобразования, исключив p e , и получим следующее:

m c 2 υ 0 — υ = h υ 0 υ ( 1 — cos θ ) .

Перейдем от частот к волнам υ 0 = c λ 0 , υ = c λ . У нас получится выражение, совпадающее с формулой Комптона, которая была получена при эксперименте:

∆ λ = λ — λ 0 = h m c ( 1 — cos θ ) = 2 h m c sin 2 θ 2 .

Проведенные теоретические расчеты, использующие квантовые представления, помогают не только объяснить эффект Комптона, но и вывести формулу нахождения длины волны с помощью фундаментальных констант m , h , c :

Λ = h m c = 2 , 426 · 10 — 3 н м .

Видео:Лекция 263 Эффект. КомптонаСкачать

Почему длина части волн не изменяется?

Согласно данным опыта, в излучении после рассеяния кроме смещенной линии есть и несмещенная, длина волны излучения которой совпадает с первоначальной. Ее наличие можно объяснить тем, что часть фотонов взаимодействует с электронами, крепко связанными с ядрами атомов. Тогда происходит обмен энергии и импульса с атомом в целом, а не только с электроном. Поскольку атом весит значительно больше, то переданная энергия фотона очень мала, следовательно, длина волны λ рассеянного излучения остается практически неизменной.

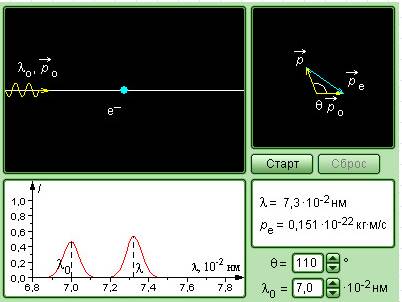
Рисунок 5 . 3 . 4 . Модель комптоновского рассеяния.

Видео:Урок 434. Фотоэффект. Законы фотоэффектаСкачать

Эффект Комптона простыми словами: что это такое, формулы

Современная физика описывает явления, которые, на первый взгляд, противоречат здравому смыслу. Знаете ли вы, что свет может взаимодействовать с электронами? В результате этих взаимодействий электрон может достичь определенной скорости, а свет… меняет свое направление и длину волны. Это явление называется эффектом Комптона. Проанализировав эту статью, вы увидите, что этот удивительный эффект имеет очень простое объяснение. Чтобы понять его, нам понадобятся лишь базовые знания механики и простые факты из современной физики.

Видео:Эффект КомптонаСкачать

Простое объяснение эффекта Комптона

Эффект Комптона — это явление, при котором свет взаимодействует с электронами. Давайте сначала уточним, что именно мы подразумеваем под словом «свет». Оказалось, что свет имеет двойственную природу — в одних экспериментах его природа волновая, в других — корпускулярная.

Рис. 1. Следует ли рассматривать свет как волны или как частицы?

Свет волновой природы — это электромагнитные волны (или электромагнитное излучение), с которыми мы знакомы. Подтверждение того, что свет может вести себя как волна, было получено в 1803 году английским физиком Томасом Янгом. Он провел серию гениальных экспериментов, в которых показал, что свет претерпевает дифракцию и интерференцию, то есть явления, характерные для волн. Эти эксперименты XIX века утвердили мнение о том, что свет является разновидностью волны.

Это мнение оставалось практически неизменным в течение 100 лет! Однако уже в то время были обнаружены явления и эффекты, которые нельзя было объяснить, исходя из того, что свет имеет только волновую природу. Фотоэлектрический эффект, заключающийся в выбросе электронов с поверхности металлов, оказался большой проблемой. Свойства этого явления противоречили волновой природе света.

В 1900 году немецким физиком Максом Планком была написана первая статья, постулирующая частичную природу света. В 1905 году на основе работы Планка световая квантовая гипотеза была представлена Альбертом Эйнштейном, также уроженцем Германской империи того времени. Эта гипотеза постулировала, что свет можно рассматривать как поток частиц. Наименьшая «порция» света (квант света) называется фотоном. Используя свою гипотезу, Эйнштейн смог объяснить фотоэлектрический эффект и его свойства. В 1921 году за это объяснение он получил Нобелевскую премию.

Давайте теперь вернемся к эффекту Комптона. Он получил свое название от имени американского физика Артура Холли Комптона. Комптон изучал рассеяние рентгеновских лучей. Полученные им результаты не соответствовали волновой природе света в то время. Для того чтобы правильно объяснить полученные результаты, Комптон, как и Эйнштейн, должен был предположить, что свет состоит из потока частиц. В 1923 году физик опубликовал работу, описывающую новый эффект, и очень скоро, в 1927 году, он получил Нобелевскую премию за свои исследования! Как видите, в то время новая, зарождающаяся отрасль физики (сейчас она называется современной физикой) была полем многих захватывающих и новаторских научных исследований.

Эффект Комптона делает известной как волновую, так и корпускулярную природу света. Этот эффект связан с взаимодействием рентгеновских и гамма-лучей с электронами. В результате этого взаимодействия электрон приобретает определенную скорость и выбрасывается, а излучение меняет направление и длину волны. Когда излучение, особенно свет, меняет направление, мы говорим, что оно рассеяно. Схема явления Комптона показана на рис. 2.

Рис. 2. Схема эффекта Комптона

В явлении Комптона излучение с длиной волны λ_f падает на свободный или слабо связанный электрон. Что это значит? «Свободный» электрон не взаимодействует ни с какими другими объектами, в то время как «слабо связанным» электрон называется тогда, когда энергия связи электрона намного меньше энергии падающего фотона.

В результате освещения электрон приобретает определенную скорость под углом φ к первоначальному направлению распространения излучения. Излучение, в свою очередь, рассеивается под углом θ к первоначальному направлению, длина волны также изменяется, и ее новое значение составляет λ_f ‘ .

Видео:Атомная и ядерная физика. Лекция 3.2. Эффект КомптонаСкачать

Формулы для расчета энергии и импульса фотона

Чтобы понять и описать, что происходит во время эффекта Комптона, давайте рассматривать рентгеновские лучи (или гамма-лучи) как поток частиц. Если бы мы использовали только волновое описание, изменение длины волны излучения не могло бы быть объяснено. Такой эффект не возникает при классическом рассеянии. Если предположить, что мы рассматриваем излучение как поток фотонов, то мы имеем дело с упругим столкновением одной частицы (фотона) с другой частицей (электроном). Упругое столкновение можно рассматривать на основе известных законов механики — должны выполняться принципы сохранения импульса и энергии:

где буквы p и E обозначают импульс и энергию частицы, соответственно. Подстрочные индексы f и e означают фотон и электрон, соответственно. «Штрихованные» индексы относится к величинам после рассеяния, «нештрихованные» индексы — к величинам до рассеяния. Итак, нам удалось свести сложный вопрос современной физики к простой механике, как при столкновении бильярдных шаров!

Для справки. Упругое столкновение — столкновение, при котором импульс и энергия системы (в классической физике — кинетическая энергия) не изменяются.

Чтобы решить приведенную выше систему уравнений и определить неизвестные значения импульса и энергии после рассеяния, необходимо разложить вектор импульса на составляющие. В нашем двумерном случае мы получаем в общей сложности три уравнения: два, описывающие импульс (в горизонтальном и вертикальном направлениях), и одно, описывающее энергию:

Что такое импульс и энергия фотона? Для их определения мы должны обратиться к двойственной природе излучения. Значение импульса фотона (частицы) связано с длиной волны света λ следующим соотношением: p_f = h / λ .

где h = 6,63 * 10 -34 Дж*с — постоянная Планка. Энергия фотона составляет: E_f = p_f * c = h*c / λ

где c = 3 * 10 8 м/с — скорость света в вакууме. Вы уже видите взаимосвязь природы волн и частиц? Чтобы объяснить явление Комптона, мы должны рассматривать излучение как поток частиц, которые, подобно пулям, сталкиваются с электронами и приводят их в движение. С другой стороны, мы не можем определить энергию и импульс фотонов, не обращаясь к их волновой природе.

Видео:Эффект КомптонаСкачать

Формулы для расчета импульса и энергии релятивистских частиц

А каковы будут импульс и энергия электрона? В явлении Комптона отражающийся электрон может достигать очень высоких скоростей, составляющих значительную долю скорости света. Это означает, что к электрону нужно относиться релятивистски. Нельзя записать импульс и энергию электрона классическим способом, потому что масса движущегося электрона отличается от его массы покоя (и зависит от скорости). Релятивистская связь между энергией E и импульсом p следующая:

E = m₀ * c 4 + p 2 * c 2

где m₀ — масса покоя. Для электрона это m₀ = 9,1*10 -31 кг. Далее мы будем обозначать массу покоя электрона через m_e. Конечно, если мы используем релятивистское выражение для движущегося электрона, то это же выражение должно быть использовано «с другой стороны уравнения» для покоящегося электрона. Когда электрон находится в состоянии покоя (до освещения), его импульс равен нулю, что означает, что мы можем выразить энергию (покоя) как: E_e = m_e * c 2 .

В релятивистской физике мы говорим, что энергия покоя связана только с тем, что тело наделено массой. В этом смысл знаменитой формулы Эйнштейна — энергия и масса эквивалентны. Увеличение энергии тела приводит к увеличению его массы.

Анализируя рис. 2, мы видим, что отдельные компоненты импульса могут быть определены простыми тригонометрическими соотношениями. Таким образом, в конечном итоге наша система уравнений принимает вид, показанный ниже. Первое уравнение относится к горизонтальной составляющей импульса, второе — к вертикальной, а третье выражает принцип сохранения энергии.

В типичном лабораторном эксперименте мы освещаем электроны излучением с фиксированной длиной волны λ и получаем, как правило, угол рассеяния фотона θ. Тогда неизвестные в приведенной выше системе уравнений имеют вид λ ‘ , p ‘ _e и φ. Для получения окончательного выражения, описывающего эффект Комптона, эта система обычно преобразуется к форме, показанной ниже. Мы рекомендуем вам провести эти расчеты самостоятельно. В Интернете вы найдете множество советов о том, как это сделать.

Δλ = λ ‘ — λ = ( h / m_e * c ) * ( 1 — cos θ )

Эта форма решения позволяет нам быстро определить разность длин волн между падающим и рассеянным фотоном. Зная длину волны падающего фотона и угол рассеяния фотона θ , мы можем быстро определить длину волны рассеянного фотона. Зная длины волн, мы можем вычислить энергии обоих фотонов, а затем, исходя из принципа сохранения энергии, энергию электрона после рассеяния.

Разница Δλ = λ ‘ — λ называется комптоновским сдвигом или комптоновским смещением. Выражение λ_c = h / m_e * c ≈ 2,43 * 10 -12 м называется комптоновской длиной волны.

Если выражаться образно, то можно сказать, что излучение после столкновения со свободными электронами меняет направление… и цвет — потому что меняется длина волны. Однако такое утверждение не совсем точно. Когда мы говорим о «цвете света», мы имеем в виду свет видимого диапазона, то есть с длиной волны от 400 до 700 нм. Комптоновское рассеяние, однако, не наблюдается для видимого излучения. Эффект возникает для рентгеновских и гамма-лучей, т.е. для излучения с на порядки большей энергией фотонов (или на много порядков меньшей длиной волны), чем видимый свет.

Видео:11 класс, 21 урок, Фотоны. Эффект КомптонаСкачать

Два случая комптоновского рассеяния

Рассмотрим теперь два крайних случая комптоновского рассеяния. Первый возникает, когда угол рассеяния фотона θ = 0°. Это означает, что фотон не меняет своего направления после столкновения с электроном. Эта ситуация показана на рис. 3. Мы видим, что:

λ ‘ — λ = ( h / m_e * c ) * (1 — 1) = 0 → λ ‘ = λ

Длина волны фотона до и после столкновения одинакова. Это означает, что фотон не передает импульс или энергию электрону. Поэтому электрон остается в состоянии покоя, а фотон продолжает двигаться без рассеяния.

Рис. 3. Случай «отсутствия» рассеяния в явлении Комптона

Другой крайний случай — когда θ = 180°. Образно говоря, фотон «отскакивает» от электрона и начинает двигаться в прямо противоположном направлении. Такая ситуация называется обратным рассеянием фотона. Тогда у нас есть:

λ = ( h / m_e * c ) * (1 + 1) = 2h / m_e * c

При обратном рассеянии разность длин волн фотона принимает максимально возможное значение. Это означает, что фотон передает электрону максимально возможную энергию и импульс. Эта ситуация показана на рис. 4.

Рис. 4. Случай обратного рассеяния в явлении Комптона