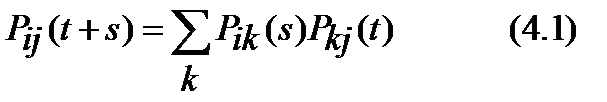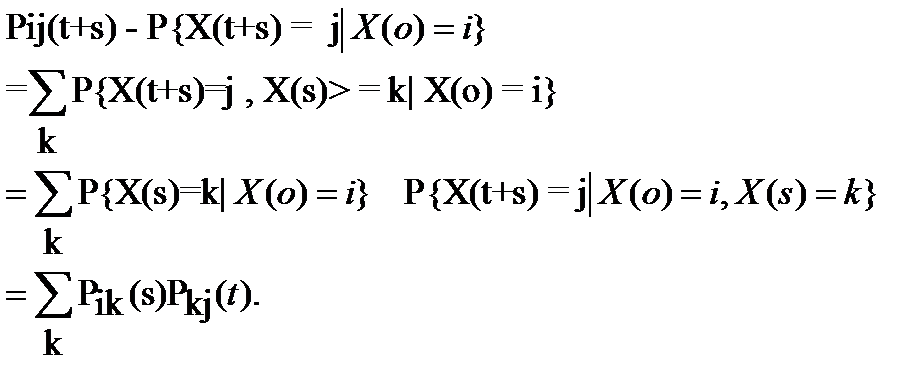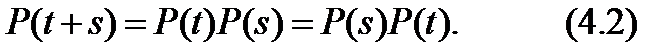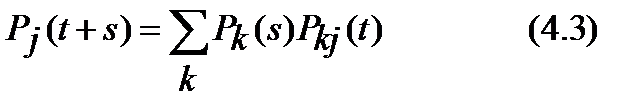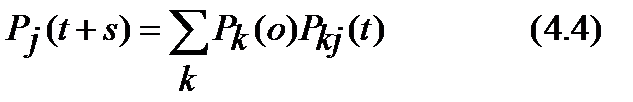Уравнение колмогорова чепмена простыми словами (2 видео)

Уравнения Колмогорова — Чепмена

Дата добавления: 2014-04-25 ; просмотров: 6147 ; Нарушение авторских прав

Переходные вероятности Р_ij(t) удовлетворяют уравнению Колмогорова – Чепмена

Это уравнение отражает тот факт, что марковская система, переходя из состояния i в состояние j за время t+s, сначала за время s из состояния i переходит в некоторое промежуточное состояние k, a затем за время t из состояния k переходит в состояние j, причем вероятность второго перехода не зависит от того, каким образом было достигнуто состояние k.

Докажем уравнение Колмогорова — Чепмена. С помощью формулы полной вероятности пишем

Здесь четвертое равенство написано на основании марковского свойства и свойства однородности процесса X(t). В матричной форме уравнение Колмогорова — Чепмена записывается как

Для безусловных вероятностей состояний р_j(t) = P<X(t) = j>, j = 0, ±1, ±2. справедливо уравнение

которое можно вывести из (4.1), если в (4.1) слева и справа умножить на р_i (0) и затем просуммировать по всем индексам i = 0, ±1 , ±2 . Если в (4.3) s = 0, то

\|	следующая лекция ==>
Марковское свойство	\|	Дифференциальные уравнения Колмогорова

Не нашли то, что искали? Google вам в помощь!

Видео:уравнение колмагороваСкачать

Математическая модель ставок Колмогорова-Чепмена

В беттинге многое зависит от случайных процессов, которые влекут за собой определенные события. Многие процессы можно предугадать и рассчитать, но некоторые все равно остаются неучтенными. Математики со всего мира изучают случайные процессы в теории вероятности, но дальше всех удалось продвинуться Колмогорову и Чепмену. В конце 1920-х годов теоретикам удалось вывести универсальное уравнение, которое расширило возможности анализа цепи Маркова.

Смысл формулы Колмогорова и Чепмена в том, чтобы высчитывать вероятности конечного состояния системы. Исходными данными будут случайные процессы, которые протекают на данный момент. Таким образом род и причины возникновения этих процессов не играют никакой роли. Ученые считали, что на исход может повлиять текущее положение дел, но не прошлое. В беттинге это можно понять так, что выбирать исход для ставки нужно только на основе самой последней информации и статистики.

Естественно, использование в анализе матча уравнения Колмогорова-Чепмена может отпугнуть рядовых прогнозистов. Они и так без особой ответственности подходят к прогнозированию в букмекерской конторе, а здесь еще и высшая математика. Кому-то может показаться, что игра не стоит свеч. Однако профессиональные игроки не дадут соврать, что уравнение Колмогорова-Чепмена значительно экономит время анализа матча. Остается только правильно его адаптировать под конкретный вид спорта.

Математические модели позволяют создать базу для ставки на основе статистических данных. Тем не менее сам анализ вероятностей на этом не заканчивается. Нужно понимать, что никакая формула не будет учитывать всех индивидуальных особенностей. В футболе немаловажную роль играют лидеры команд, а также место проведения встречи. В теннисе многое зависит от погодных условий (дождь, солнце и т.д.). К тому же, каждая ставка требует индивидуального подхода к анализу физического и эмоционального состояния соперников.

Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Ошибка
404

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.