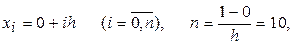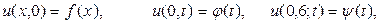Уравнение колебания струны методом сеток

Видео:Неоднородное уравнение колебания струныСкачать

8.1. Разностный метод для уравнения колебаний

8.1.1. Уравнение колебаний струны. Явная схема

Рассмотрим задачу о малых колебаниях натянутой струны с распределенной по длине нагрузкой f(x, t) (см. рис. 8.1):

(8.11)

(8.12)

(8.13)

Струна совершает плоские колебания, т. е. точки струны перемещаются параллельно плоскости t = 0.

Функция u(x, t) выражает смещение точки x струны в момент времени t от прямолинейной формы.

Начальные условия (8.12) означают следующее. Форма струны в начальный момент времени t = 0 выражается функцией μ(x). Скорость перемещения точки x струны в момент времени t = 0 равна значению функции μ0(x).

Краевые условия (8.13) говорят о том, что левый конец струны с течением времени совершает смещение μ1(t), а правый конец — смещение μ2(t).

Если концы струны закреплены, то μ1(t) = μ2(t) = 0.

Мы предполагаем, что начальные условия (8.12) и краевые условия (8.13) должны быть согласованы между собой в угловых точках, т. е. выполнены условия .

На рис. 8.1 представлен случай, когда , .

Введем сеточную область (рис.8.2, a)). В прямоугольной области зададим точки:

(8.14)

Рассмотрим уравнение (8.11) в точках , , , и заменим производные разностными формулами

, (8.15)

Обозначим через приближенные значения искомой функции в точках . Тогда из уравнения (8.11) получим разностное уравнение (разностную схему), которое аппроксимирует уравнение (8.11) с порядком O(h2 + τ2):

(8.16)

На рис. 8.2 b) изображен шаблон «крест» разностного уравнения (8.16). Разностное уравнение (8.16) связывает значения неизвестной функции на трех слоях (k – 1, k, k + 1).

На слое k = 0 заданы начальные условия (8.12), из которых следует, что

. (8.17)

Чтобы найти значения неизвестной функции на слое k = 1, используем условие для производной ut(x, 0) из (8.12). Для этого построим разложение в ряд Тейлора

. (8.18)

Из уравнения (8.11), учитывая первое условие в (8.12), выразим вторую производную

. (8.19)

Теперь, учитывая условие в (8.12), из (8.18), (8.19) выводим формулу для вычисления значений функции на первом слое:

. (8.20)

С учетом (8.13), окончательно получим для приближенных значений искомой функции на первом слое формулы

. (8.21)

Учитывая граничные условия (8.13) из (8.16) выводим формулы для вычисления значений на слоях :

(8.22)

Мы получили явные формулы (8.17), (8.21), (8.22) решения разностной задачи.

Разностная схема называется устойчивой, если она имеет единственное решение и малым изменениям исходных данных отвечают малые изменения решения.

Приведем без доказательства (доказательство можно найти в [9]) следующий факт: для выполнения условия устойчивости разностной схемы (8.16) необходимо и достаточно, чтобы выполнялось условие Куранта cτ 0 находим методом прогонки, последовательными вычислениями в несколько этапов.

2.1. Вычислим правые части (8.26):

(8.29)

2.2. Вычислим прогоночные коэффициенты:

(8.30)

(8.31)

(8.32)

2.3. Вычислим решение ui,k+1:

(8.33)

(8.34)

Отметим преимущества неявной схемы перед явной схемой:

В явной схеме надо выбирать шаги h и τ так, чтобы выполнялось условие устойчивости (условие Куранта) cτ

Видео:Уравнение колебания струны. Решение методом ДаламбераСкачать

Метод сеток для уравнения гиперболического типа

Рассмотрим уравнение свободных колебаний однородной ограниченной струны (гиперболического типа) при отсутствии внешней силы

, (6)

где u=u(x,t) – смещение точки однородной струны с абсциссой х, t – время, а – постоянная, зависящая от физических свойств струны.

Будем искать решение уравнения (6) при заданных начальных и краевых условиях

(7)

(8)

Решим эту смешанную задачу методом сеток. Как и в случае параболического уравнения, покроем полосу , прямоугольной сеткой где

(n – целое) и

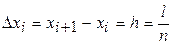
На сетке 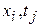приближенно заменим дифференциальное уравнение (6) соответствующим конечно-разностным уравнением.

Пользуясь симметричными формулами для производных, будем иметь

. (9)

При уравнение (9) упрощается и принимает вид ,

откуда . (10)

Решение одного варианта

1. Используя метод сеток, составить решение смешанной задачи для дифференциального уравнения параболического типа 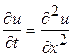(уравнение теплопроводности) при заданных начальных условиях

где 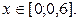Решение выполнить при для с четырьмя десятичными знаками, считая .

Параболическое уравнение решается методом сеток постепенным переходом от значений функции к значениям ; причем где

Вычисления производятся по формуле

Все расчеты приведены в таблице:

2. Используя метод сеток, составить решение смешанной задачи для уравнения колебания струны с начальными условиями и краевыми условиями Решение выполнить с шагом , определяя значения функции с четырьмя десятичными знаками, причем .

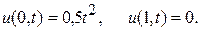
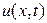
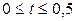
Для решения воспользуемся соотношением

,

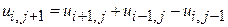
При этом а для определения можно использовать один из возможных приемов, например,

,

.

Кроме того,

Решая по указанным формулам удобно выполнять в таблице, которая и является решением данной задачи.

Порядок заполнения таблицы:

1. Вычисляем значения при и записываем их в первую строку (она соответствует значению t₀=0).

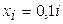
2. Вычисляем значения при и записываем их в первый столбец таблицы (он соответствует значению x₀=0).

3. Заносим значения в последний столбец таблицы (он соответствует значению x₁₀=1,0)

4. Вычисляем значения по формуле , где и берутся из первой строки таблицы, а . Результаты записываем во вторую строку таблицы.

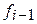
5. Вычисляем значения в последующих строках по формуле , где значения берутся из двух предыдущих строк таблицы.

Задания

1. Используя метод сеток, составить решение смешанной задачи для дифференциального уравнения параболического типа 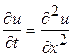(уравнение теплопроводности) при заданных начальных условиях

где Решение выполнить при для с четырьмя десятичными знаками, считая .

Вариант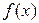
cos2x	1-6t	0,3624
x(x+1)	0	2t+0,96
1,2+lg(x+0,4)	0,8+t	1,2
sin2x	2t	0,932
3x(2-x)	0	t+2,52
1-lg(x+0,4)	1,4	t+1
sin(0,55x+0,03)	t+0,03	0,354
2x(1-x)+0,2	0,2	t+0,68
sinx+0,08	0,08+2t	0,6446
cos(2x+0,19)	0,932	0,1798
2x(x+0,2)+0,4	2t+0,4	1,36
lg(x+0,26)+1	0,415+t	0,9345
sin(x+0,45)	0,435-2t	0,8674
0,3+x(x+0,4)	0,3	6t+0,9
(x-0,2)(x+1)+0,2	6t	0,84
x(0,3+2x)	0	6t+0,9
sin(x+0,48)	0,4618	3t+0,882
sin(x+0,02)	3t+0,02	0,581
cos(x+0,48)	6t+0,887	0,4713
lg(2,63-x)	3(0,14-t)	0,3075
1,5-x(1-x)	3(0,5-t)	1,26
cos(x+0,845)	6(t+0,11)	0,1205
lg(2,42+x)	0,3838	6(0,08-t)
0,6+x(0,8-x)	0,6	3(0,24+t)
cos(x+0,66)	3t+0,79	0,3058
lg(1,43+2x)	0,1553	3(t+0,14)
0,9+2x(1-x)	3(0,3-2t)	1,38
lg(1,95+x)	0,29-6t	0,4065

2. Используя метод сеток, составить решение смешанной задачи для уравнения колебания струны с начальными условиями и краевыми условиями Решение выполнить с шагом , определяя значения функции с четырьмя десятичными знаками, причем .

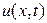
Вариант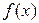
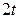			-1
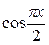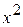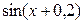	2	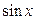0,3
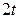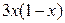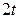			1,5
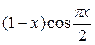		2
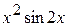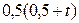			2,25
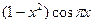		0,5
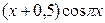		0,5
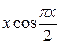		0,4
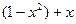			0,9
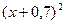		0,5

Литература

1. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения)/ В.М.Вержбицкий. – М.: «Высшая школа», 2000. – 266с.

2. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения)/ В.М.Вержбицкий. – М.: «Высшая школа», 2001. – 382 с.

3. Волков Е.А. Численные методы: учебное пособие/ Е.А.Волков. СПб.: Изд-во «Лань», 2004. – 256с.

4. Демидович Б.П. Основы вычислительной математики/ Б.П.Демидович, И.А. Марон. – М.: Изд-во «Наука», 1970. – 664с.

5. Демидович Б.П. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения: учебное пособие/ Б.П.Демидович, И.А.Марон, Э.З.Шувалова; Под ред. Б.П.Демидовича. – СПб.: Изд-во «Лань», 2008. – 400с.

6. Заварыкин В.М. Численные методы: учеб. пособие для студентов физ.-мат. спец. пед. ин-тов / В.М.Заварыкин, В.Г.Житомирский, М.П.Лапчик. – М.: Просвещение, 1990. – 176с.

7. Воробьева Г.Н. Практикум по численным методам/ Г.Н.Воробьева, А.Н. Данилова – М.: Высш. шк., 1979. – 184с.

8. Лапчик М.П. Численные методы: учебное пособие для студ. вузов / М.П.Лапчик, М.И.Рагулина, Е.К.Хеннер; Под ред.М.П.Лапчика. – М.: Издательский центр «Академия», 2005. – 384с.

9. Формалев В.Ф. Численные методы/ В.Ф.Формалев, Д.Л.Ревизников. – М.: ФИЗ-МАТЛИТ, 2004. – 400 с.

Содержание

Лабораторная работа №1. 1

Элементарная теория погрешностей. 2

Лабораторная работа №2. 6

Решение нелинейных уравнений методом половинного деления. 6

🎦 Видео

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Колебания струныСкачать

УМФ, 22.12, вывод уравнения колебаний струныСкачать

6-2. Метод сетокСкачать

Урок 376. Колебания струн, стержней и воздушных столбовСкачать

4.1 Колебания полуограниченной струны с закрепленным и свободным концомСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Вывод уравнения колебаний струныСкачать

Уравнение колебаний струны. Метод Фурье - 1Скачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Численные методы математической физики - Метод сеток решения граничной задачиСкачать

решение задачи колебание струны конечной длиныСкачать

5. Решение волнового уравнения на отрезке методом ФурьеСкачать

3.1 Формула Даламбера, решение волнового уравнения на бесконечной прямойСкачать

2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать

УМФ решение краевой задачи уравнения колебания струны. Метод Фурье. Задача Штурма–Лиувилля. Пример.Скачать