Уравнение колебания бесконечной струны его решение (6 видео)

Лекция 2. Вывод уравнения колебания струны

Рассмотрим струну длины l

Струной будем называть тонкую туго натянутую упругую нить.

При построени математической модели колебаний струны будем рассматривать малые колебания, происходящие в одной и той же плоскости. Пусть в состояниии покоя струна расположена вдоль оси Ox на отрезке [0,l] и при колебании каждая точка перемещается перпендикулярно оси (поперечные колебания). Тогда отклонение любой точки струны в произвольный момент времени U есть функция U(x,t) (см. рис.2).

Предположим, что натяжение столь велико, что силой тяжести и сопротивлением при изгибе можно пренебречь. Кроме того, в силу малости колебаний, будем пренебрегать также величинами высшего порядка малости по сравнению с производной U_x.

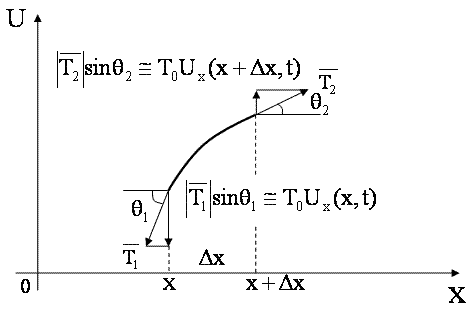
Рис. 3

Выделим малый участок струны (см. рис.3) и рассмотрим силы, действующие на него. Так как струна не сопротивляется изгибу, то ее натяжение направлено по касательной к струне в точке x. Более того, в рамках наших предположений можно считать величину силы натяжения постоянной. В самом деле, длина любого участка струны (величиной U_x 2 можно пренебречь). С ледовательно, в соответствии с законом Гука _.

Пусть ρ ( x )- линейная плотность в точке x , а γ ( x , t )- плотность внешних сил, действующих на струну в момент времени t, и направленных перпендикулярно Ox .

Результирующая сила, действующая на участок струны [ x , x +∆ x ] в направлении перпендикулярном оси OX , равна (см. рис. 3)

При выводе этой формулы учитываем, что при малых колебаниях

По второму закону Ньютона произведение массы на ускорение равно действующей силе mw = F , где w=U_tt, поэтому

ρ ∆ xU_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]+ γ ( x , t ) ∆ x .

Разделим обе части равенства на Δx и устремим Δx к нулю:

ρ ( x ) U_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]/ ∆ x + γ ( x , t ) .

Это уравнение называется уравнением вынужденных колебаний струны. Если струна однородная, то есть ρ ( x )= const , то уравнение (3) обычно записывают в виде

U_tt = a 2 U_xx + f ( x , t ),где a 2 = T ₀/ ρ ; f ( x , t )= γ ( x , t ) / ρ .

В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны

Уравнения (3) и (4) являются одномерными волновыми уравнениями (соответственно, неоднородным и однородным).

Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.

Содержание

Начальные условия и граничные условия.
Уравнение колебания бесконечной струны его решение
27.1. Вывод уравнения колебаний струны
27.2. Начальные и краевые условия. Задача Коши
27.3. Задача о свободных колебаниях бесконечной струны. Метод Д’Аламбера
Электронная библиотека
📺 Видео

Начальные условия и граничные условия.

Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за t=0. В результате возникает задача Коши. Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.

Для волнового уравнения U_tt = a 2 U_xx задаются два начальных условия U | _{t =0} = φ ( x ), U_t | _{t =0} = ψ ( x ). Иногда их записывают иначе: U ( x , 0) = φ (х), U_t ( x , 0) = ψ (х). Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие — начальные скорости точек струны. В случае волнового уравнения U_tt = a 2 Δ U на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ , соответственно, будут зависеть от двух или трех переменных.

Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными условиями или краевыми условиями.Для уравнения колебаний струны часто задаются условия U | _{x =0} = 0, U | _{x = l} = 0. Иначе их записывают еще и гак: U (0, t )=0, U ( l , t ) = 0. Эти условия физически означают, что концы струны закреплены (то есть отклонения при х = 0 и при х = l в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, U_x |_х=0= 0 , U_x |_х= _l = 0. Такие условия возникают в следующей задаче.

Пусть концы сруны перемещаются вдоль вертикальных направляющих без трения (см. рис.4).

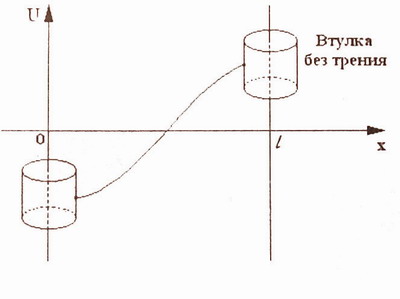
рис.4

Так как вертикальные силы, действующие на левый и правый концы струны, определяютя выражениями T ₀ U_x ( O , t ) и T ₀ U_x (l, t ) (см рис. 2), то записанные выше условия означают, что на концы струны не действуют никакие силы(поэтому такие условия называют еще условиями свободных концов).

Как было уже сказано, волновое уравнение U_tt = a 2 U_xx описывает не только колебания струны, но и другие волновые процессы, к примеру, продольные колебания пружины, продольные колебания стержня, крутильные колебания вала. В этих задачах возникают граничные условия и других видов. Подробно такие задачи мы изучать не будем. Однако приведем основные типы граничных условий. Обычно рассматривают три типа:

Граничные условия (5), (6) и (7) называются однородными, если правые части g₁(t) и g₂(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.

Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных — время. Г раницей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис. 5 ) .

К примеру, граничное условие (однородное) первого рода на плоскости записывается в виде U|_Γ=О, в пространстве U|_Ω=0. Граничное условие второго рода на плоскости имеет вид ,а в пространстве . Конечно, физический смысл этих условий разный для различных задач.

При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)= φ(x), U_t (x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называется первой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.

Видео:Неоднородное уравнение колебания струныСкачать

Уравнение колебания бесконечной струны его решение

А. А. Гусак. Высшая математика. Том 2.
Глава 27. Простейшие дифференциальные уравнения математической физики

В этой главе рассматриваются некоторые уравнения математической физики, т.е. уравнения с частными производными второго порядка, к которым приводят следующие задачи: задача о колебаниях струны, задача о распространении тепла и др.

27.1. Вывод уравнения колебаний струны

Рассмотрим туго натянутую струну, закрепленную на концах. Выведем струну из положения равновесия (оттянув ее или ударив по ней), струна начнет колебаться.

Предположим, что любая точка струны колеблется по прямой, перпендикулярной к исходному положению струны, и струна все время находится в одной и той же плоскости.

Выберем в этой плоскости декартову прямоугольную систему координат Охu. В качестве оси Ох возьмем прямую, на которой находилась струна в положении равновесия, за ось Оu примем прямую, проходящую через левый конец струны и перпендикулярно к оси Ох (рис. 27.1).

Отклонение струны от положения равновесия обозначим через u; очевидно, u зависит от абсциссы х точки струны и времени t, т.е. u = u(х, t).

При фиксированном t графиком функции u = u(х, t) в плоскости Охu является форма струны в данный момент времени t. Угловой коэффициент касательной к графику в точке с абсциссой х равен частной производной по х от функции u(х, t) т.е.

где α = α (x, t) – угол наклона касательной.

Чтобы составить представление о колебаниях струны, необходимо начертить ряд графиков функции u = u(х, t) при различных значениях t.

При фиксированном значении х функция u = u(х, t) определяет закон движения точки с абсциссой х. Эта точка движется по прямой, параллельной оси Оu. Скорость и ускорение указанного движения выражаются соответственно формулами

Будем изучать малые колебания струны, т.е. такие, при которых угол α = α (x, t) (угол наклона касательной к графику функции u = u(х, t) при каждом фиксированном значении t) настолько мал, что его квадратом можно пренебречь, т.е. приближенно считать

то отсюда следует, что

sin α = α, cos α = 1.

tg α – sin α = tg α(1 – cos α) = tg α · 0 = 0 ,

Принимая во внимание (27.3) – (27.5), заключаем, что

tg² α = 0 , или

Следовательно, длина дуги струны, ограниченной точками M1(x1, u1), M2(x2, u2) выразится формулой

Соотношение (27.7) означает, что длина любого участка струны остается постоянной.

Будем предполагать струну абсолютно гибкой, что означает следующее: если удалить участки ОМ1, M2L (см. рис. 27.1), то их действия на участок М1М2 заменяются соответственно действием сил натяжения T1 и Т2, направленных по касательным к графику функции u = u(х, t) в точках М1 и М2 (рис. 27.2). Поскольку по предположению точки струны движутся по прямым, параллельным оси Оu, то сумма проекций сил T1, Т2 на ось Ох равна нулю. Проектируя эти силы на ось Ох, получаем T2сos α2 – T1cos α1 = 0, где T1, Т2 – величины сил T1, Т2.

На основании второго из равенств (27.4) заключаем, что T1 = T2 т.е. величина силы натяжения остается постоянной. Обозначая ее через T, получаем

Проектируя силы T1, Т2 на ось Оu, находим

С учетом равенства (27.1) получаем

где х – абсцисса точки М1; х + Δх – абсцисса точки М2.

Применяя теорему Лагранжа о конечном приращении дифференцируемой функции, находим, что

поэтому проекция сил натяжения T1 и Т2 на ось Ох выразится формулой

Предположим, что на струну действуют также внешние силы, параллельные оси Оu, плотность распределения* которых равна g(x, t), тогда величина равнодействующей этих сил, приложенных к участку М1М2, приближенно равна g(x, t)Δx. Силами сопротивления внешней среды пренебрегаем.

* Под плотностью понимают предел средней плотности распределения сил на данном отрезке, когда длина отрезка стремится к нулю; средняя плотность – отношение величины равнодействующей сил к длине отрезка, на котором они приложены.

Будем считать струну однородной, обозначим через ρ ее линейную плотность, тогда масса участка М1М2 выразится так: ρ М1М2 = ρ Δх, m = ρ Δх

В соответствии со вторым законом Ньютона mw = F (произведение массы на ускорение равно действующей силе) получаем

Уравнение (27.10) называется уравнением колебаний струны, или одномерным волновым уравнением.

Если g(x, t) = 0 (внешние силы отсутствуют), то уравнение (27.10) принимает вид

Уравнение (27.12) называется уравнением свободных колебаний, уравнение (27.10) — уравнением вынужденных колебаний струны.

27.2. Начальные и краевые условия. Задача Коши

Чтобы из множества решений уравнения с частными производными второго порядка выбрать определенное решение, необходимо задать дополнительные условия.

Так, в случае уравнения (27.10) или (27.12) нужно указать отклонение и скорость движения в начальный момент времени t0 (будем полагать t0 = 0), т.е.

где f(x), F(x) – заданные функции, а также зафиксировать отклонения концов струны. Поскольку концы закреплены, то

где l – длина струны.

Условия (27.13) называются начальными условиями, а условия (27.14) – краевыми (или граничными) условиями.

Итак, задача о свободных колебаниях струны ставится следующим образом. Найти решение u = u(х, t) линейного однородного уравнения с частными производными второго порядка , удовлетворяющее начальным условиям u(х, 0) = f(x), u'(х,0) = F(x) и краевым условиям u(0, t) = 0, u(l, t) = 0.

Функции f(х) и F(x) определены на отрезке [0, l], из краевых условий следует, что f(0) = 0, f(l) = 0. Можно доказать, что при некоторых предположениях относительно функций f(x) и F(x) поставленная задача имеет единственное решение.

В случае, когда предполагается, что струна является неограниченной, граничные условия не налагаются.

Задача о свободных колебаниях неограниченной струны ставится так. Найти решение u = u(х, t) уравнения с частными производными второго порядка , удовлетворяющее начальным условиям

где f(x) и F(x) – заданные функции, определенные на всей действительной оси. Эта задача называется задачей Коши.

27.3. Задача о свободных колебаниях бесконечной струны. Метод Д’Аламбера

Как уже отмечалось, задача о свободных колебаниях бесконечной струны, или задача Коши, состоит в следующем.

Найти решение u = u(х, t) линейного однородного уравнения

удовлетворяющее начальным условиям

где f(х), F(x) – заданные функции, определенные в бесконечном промежутке (-∞, +∞).

Уравнение (27.15) перепишем так: и (положив t = у) сравним его с уравнением (26.9). Поскольку В² — АС = а² > 0, то уравнение является уравнением гиперболического типа.

Уравнение характеристик Ady² — 2Bdxdy + Cdx² = 0 принимает вид a²dt² — dx² = 0 или dx² — a²dta² = 0. Оно распадается на два уравнения dx – adt = 0, dx + adt = 0, откуда получаем х – at = С1, х + at – С1.

Введя новые переменные ξ и η по формулам

преобразуем уравнение (27.15) к каноническому виду.

Выражаем частные производные по переменным х, t через частные производные по ξ, η :

Подставляя в уравнение (27.15) выражения для частных производных второго порядка, получаем

Проинтегрируем последнее уравнение. Положим тогда

Следовательно, , или u = φ(ξ) + ψ(η) , где φ(ξ), ψ(η) – произвольные дважды дифференцируемые функции своих аргументов. Принимая во внимание (27.17), последнюю формулу можно записать так:

Формула (27.18) определяет общее решение уравнения (27.15).

Среди всех этих решений найдем то, которое удовлетворяет условиям (27.16), Для функции (27.18) и ее частной производной по t

условия (27.16) принимают вид

Второе равенство проинтегрируем по отрезку [0, х]. Обозначив переменную интегрирования через z получим

где С = φ (0) + ψ (0)

Это уравнение и первое из уравнений (27.19) позволяют определить функции φ (x) и ψ (x):

Подставляя в эти формулы вместо х соответственно х – at и х + at, получаем

В соответствии сформулой (27.18) находим

Формула (27.20) представляет решение Д’Аламбера рассматриваемой задачи Коши для уравнения колебаний неограниченной струны. Читателю предлагается непосредственной проверкой убедиться в том, что функция (27.20) удовлетворяет уравнению (27.15) и условиям (27.16).

А. А. Гусак. Высшая математика. Том 2. Стр. 247-253.

Видео:Уравнение колебания струны. Решение методом ДаламбераСкачать

Электронная библиотека

Рассмотрим задачу о колебаниях бесконечной струны. Если представить себе очень длинную струну, то ясно, что на колебания, возникшие в ее средней части, концы струны не будут оказывать заметного влияния. Так, если взять длинную натянутую веревку и слегка качнуть ее в середине, то по веревке влево и вправо побегут волны.

Картина начнет искажаться только тогда, когда волны дойдут до концов веревки и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов струны, мы, тем самым, не будем учитывать влияния отраженных волн.

Таким образом, мы приходим к задаче о свободных колебаниях неограниченной струны, которая формулируется так: решить однородное линейное дифференциальное уравнение гиперболического типа

при начальных условиях

где функции и заданы на всей числовой оси. Никакие другие условия на искомую функцию не накладываются. Такая задача называется задачей с начальными условиями, или задачей Коши. Метод ее решения называется методом Даламбера или методом бегущих волн.

Уравнение характеристик распадается на два:

Характеристиками являются прямые:

Введя новые переменные , получим канонический вид уравнения колебаний:

Интегрируя это уравнение по , получим:

Интегрируя последнее уравнение по (при фиксированном значении ), будем иметь:

Полученный общий интеграл запишем, подставив и :

Учитывая начальные условия (4.19), получим:

Интегрируя уравнение (4.22), получим:

Решая уравнение (4.23) совместно с уравнением (4.21) будем иметь:

Учитывая, что функции и определены для любого аргумента, заменяем x в уравнении (4.24) на и в уравнении (4.25) на .

Подставляя полученные выражения в уравнение (4.20), получим:

Выражение (4.26) называется формулой Даламбера или решением Даламбера задачи Коши для уравнения колебаний неограниченной струны. Она показывает также существование и единственность решения данной задачи.

Выясним физический смысл полученного решения. Рассмотрим два частных случая.

Пусть начальные скорости точек струны равны нулю, и струна колеблется в результате начального отклонения. В этом случае в формуле (4.26) надо положить . Тогда

Колебание можно рассматривать как наложение (суперпозицию) колебаний двух волн:

· первая волна распространяется со скоростью a вправо (прямая волна);

· вторая волна распространяется с той же скоростью влево (обратная волна).

В начальный момент времени t = 0 профили обеих волн совпадают и повторяют начальное отклонение струны с половинной амплитудой.

Пусть теперь начальное смещение , а отлично от нуля в промежутке , а вне этого промежутка . В таком случае говорят, что струна имеет только начальный импульс (волна импульса). Тогда в соответствии с (4.26) решение имеет вид:

Используя выражение (4.29), запишем уравнение (4.28) в виде:

То есть, по струне распространяются две волны импульса: прямая и обратная , а результирующая волна является суммой (суперпозицией) этих волн.

Вывод: действие импульса заключается в том, что с течением времени точки струны сдвигаются на отрезок, определяемый интегралом (4.28) и остаются в этом положении. Волна как бы оставляет след после своего прохождения.

Полученные результаты для колебаний бесконечной струны не могут быть применены к реальному колебанию физической струны. Действительно, при их выводе не были учтены многие факторы. В частности, опыт учит нас, что струна какой угодно длины, выведенная из положения равновесия или ударенная, колеблется. Законы колебания бесконечной струны (4.27) и (4.28) этого не показывают, потому что колебания конечной струны происходят вследствие отражения отклонений от закрепленных концов струны, а при рассмотрении бесконечной струны мы не учитываем влияния концов. Поэтому практически решения уравнений (4.27) и (4.28) применимы только для таких моментов t, для которых отклонения точек струны не успели дойти до ее концов. Кроме того, начальные функции и должны быть такими, чтобы в течение всего процесса было малой величиной, которой можно пренебречь по сравнению с единицей.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00