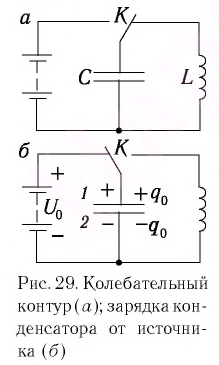
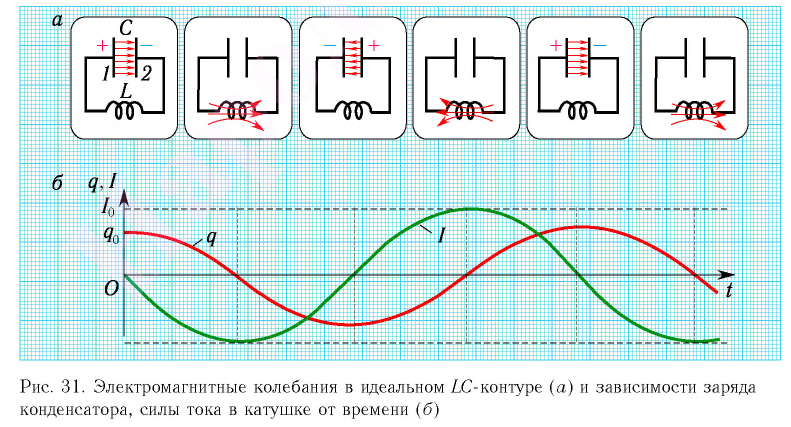
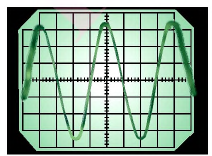
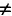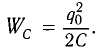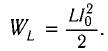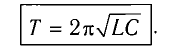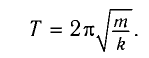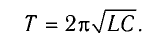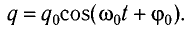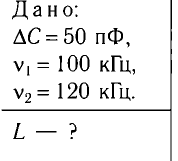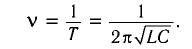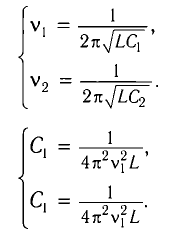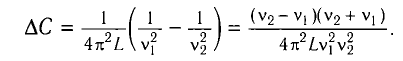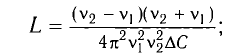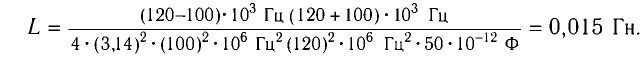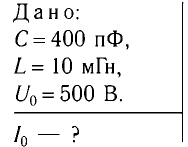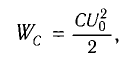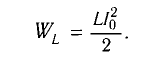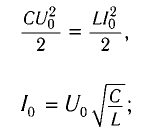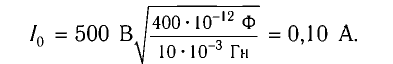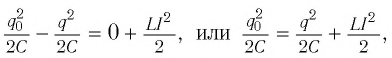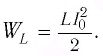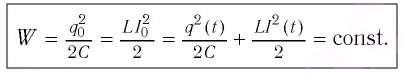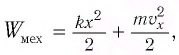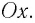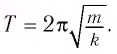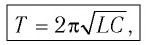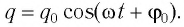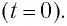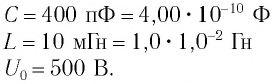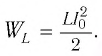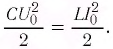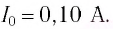Для возбуждения в контуре колебаний предварительно заряжают конденсатор, сообщая его обкладкам заряд ±q. Тогда в начальный момент времени t=0 (рис. 19, а) между обкладками конденсатора возникнет электрическое поле. Если замкнуть конденсатор на катушку индуктивности, конденсатор начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Когда конденсатор полностью разрядится, энергия электрического поля конденсатора полностью перейдет в энергию магнитного поля катушки (рис. 19, б). Начиная с этого момента ток в контуре будет убывать, и, следовательно, начнет ослабевать магнитное поле катушки, тогда в ней согласно закону Фарадея индуцируется ток, который течет в соответствии с правилом Ленца в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 19, в). Далее те же процессы начнут протекать в обратном направлении (рис. 19, г), и система к моменту времени t=Т (Т – период колебаний) придет в первоначальное состояние (рис. 19, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора, то есть начнутся периодические незатухающие колебания величины заряда q на обкладках конденсатора, напряжения UC на конденсаторе и силы тока I, текущего через катушку индуктивности. Согласно закону Фарадея напряжение UC на конденсаторе определяется скоростью изменения силы тока в катушке индуктивности идеального контура, то есть :
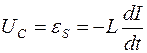
Исходя из того, что UC=q/C, а I=dq/dt, получаем дифференциальное уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
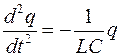
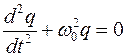
Решением этого дифференциального уравнения является функция q(t), то естьуравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
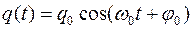
где q(t) – величина заряда на обкладках конденсатора в момент времени t;
q0 – амплитуда колебаний заряда на обкладках конденсатора;
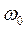
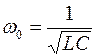
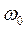
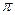
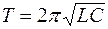
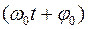
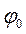
Уравнение свободных затухающих гармонических колебаний.В реальном колебательном контуре учитывается, что кроме катушки индуктивностью L, конденсатора емкостью С, в цепи также имеется резистор сопротивлением R,отличным от нуля, что является причиной затухания колебаний в реальном колебательном контуре. Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.
Для цепи реального колебательного контура напряжения на последовательно включенных конденсаторе емкостью С и резисторе сопротивлением R складываются. Тогда с учетом закона Фарадея для цепи реального колебательного контура можно записать:
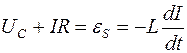
где 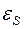
IR – напряжения на резисторе.
Исходя из того, что I=dq/dt, получаем дифференциальное уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
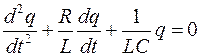
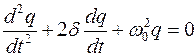
где 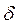
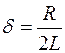
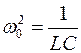
Решением полученного дифференциального уравнения является функция q(t), то естьуравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
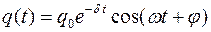
где q(t) – величина заряда на обкладках конденсатора в момент времени t;
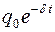
q0 – начальная амплитуда затухающих колебаний заряда;
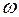
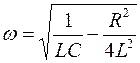
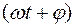
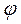
Период свободных затухающих колебаний в реальном колебательном контуре :
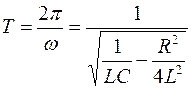
Вынужденные электромагнитные колебания. Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо в процессе колебаний компенсировать потери энергии. Такая компенсация в реальном колебательном контуре возможна с помощью внешнего периодически изменяющегося по гармоническому закону переменного напряжения U(t):
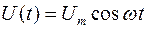
В этом случае дифференциальное уравнение вынужденных электромагнитных колебанийпримет вид:
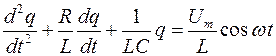
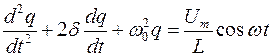
Решением полученного дифференциального уравнения является функция q(t):
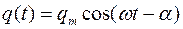
В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими, а амплитуда 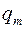
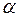
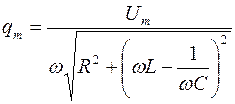
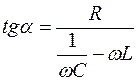
Отсюда следует, что амплитуда колебаний величины заряда 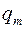
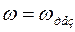
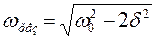
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающего переменного напряжения к частоте, близкой частоте 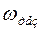
Тема 10. Электромагнитные волны
Согласно теории Максвелла электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость 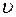
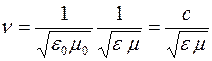
где 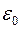
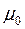
e и m – соответственно электрическая и магнитная проницаемости среды,
с – скорость света в вакууме ( 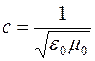
В вакууме (e = 1, m = l) скорость распространения электромагнитных волн совпадает со скоростью света( с ), что согласуется с теорией Максвелла о том,
что свет представляет собой электромагнитные волны.
По теории Максвелла электромагнитные волны являются поперечными,то есть векторы 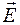
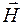
скорости распространения волны, причем векторы 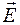
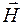
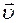
Из теории Максвелла следует также, что в электромагнитной волне векторы 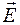
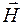

Уравнение плоской монохроматической электромагнитной волны (индексы у и z при Е и Н подчеркивают лишь то, что векторы 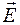
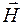
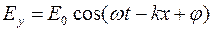

где E0 и Н0– соответственно амплитуды напряженностей электрического и магнитного полей,
w – круговая частота волны, 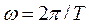
k – волновое число, 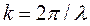
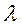
j – начальная фаза колебаний (начальная фаза колебаний j имеет одинаковое значение как для колебания электрического, так и магнитного векторов, так как в электромагнитной волне эти колебания происходят в одинаковых фазах).
Энергия электромагнитных волн. Электромагнитные волны переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей wэл электрического и wм магнитного полей:
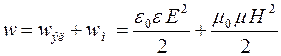
Учитывая выражение связи между величинами Е и Н , можно получить, что суммарная плотность энергии электрического и магнитного полей:
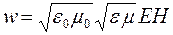
Умножив плотность энергии w на скорость 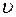
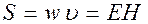
Tax как векторы 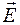
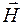
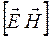
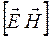
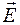
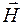
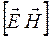
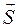
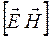
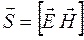
Итак, вектор 
- Колебательный контур в физике — формулы и определения с примерами
- Колебательный контур и свободные электромагнитные колебания в контуре
- Электромагнитные колебания
- Колебательный контур
- Энергетические превращения в колебательном контуре
- Электромеханические аналогии
- Гармонический закон колебаний в контуре
- Вынужденные электромагнитные колебания
- 📺 Видео
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Колебательный контур в физике — формулы и определения с примерами
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
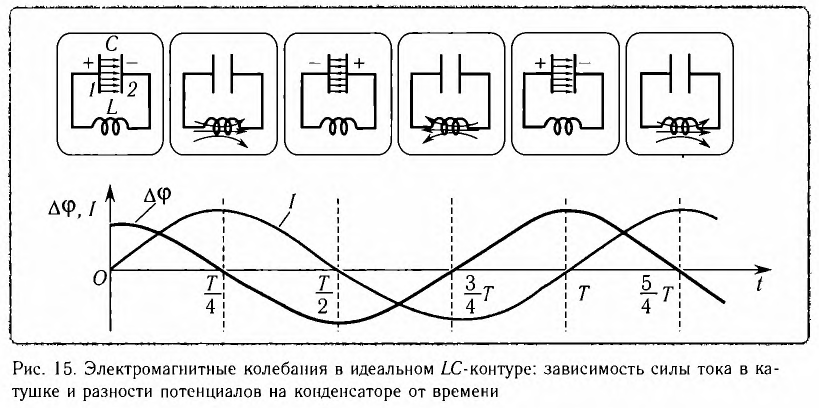
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +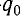

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений 

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
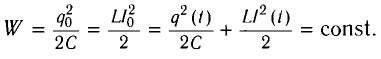
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
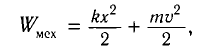
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 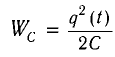
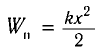
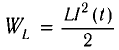
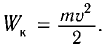
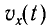
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 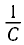
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
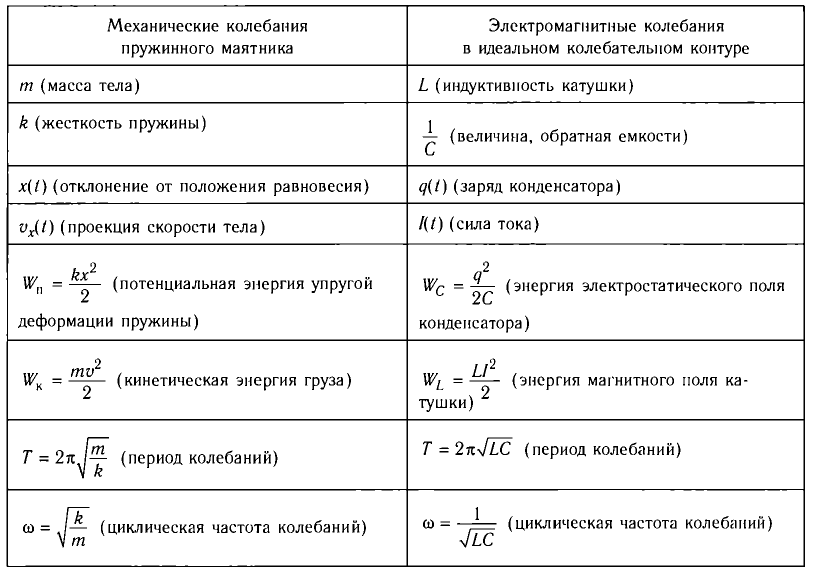
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 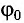
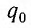
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 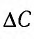
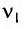
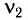
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (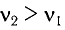
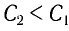
Из условия задачи получаем систему уравнений
Откуда
Вычитая из первого уравнения второе, получаем
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 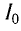
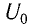
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 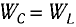
откуда
Ответ: 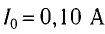
Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 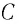
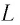
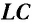
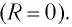
Подключив (при помощи ключа 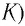
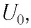
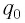
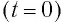
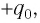
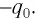
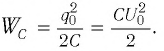
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 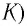
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 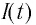
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 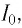
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 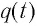
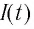
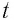
В момент полной разрядки конденсатора 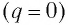
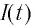
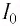
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 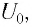
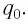
Таким образом, в идеальном 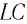
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 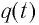
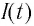
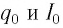
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 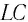
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 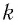
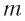
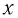
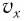
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 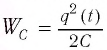
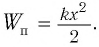
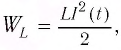
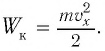
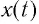
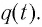
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 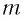
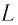
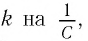
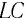
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 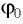
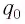
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 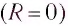
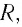
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 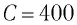
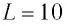
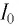
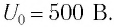
Дано:

Решение
Максимальная энергия электростатического поля конденсатора:
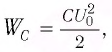
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 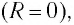
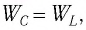
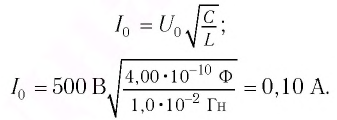
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 8. Перезарядка конденсатора. Плотность тока смещения. Ток смещения. Физика 11 классСкачать

Электромагнитные колебания
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Колебательный контур
Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.
Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.
Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.
Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.
Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.
Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.
Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.
Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).
Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.
Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.
Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.
Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.
Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.
Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).
Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.
Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.
Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.
Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .
Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).
Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.
Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).
Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.
Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).
Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.
Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).
Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.
Аналогия. Маятник вернулся в исходное положение.
Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!
Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.
В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.
Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.
Видео:Урок 355. Затухающие электромагнитные колебания.Скачать

Энергетические превращения в колебательном контуре
Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .
Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.
Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:
Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:
В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:
Соотношение (1) применяется при решении многих задач.
Видео:Зарядка конденсатора в электрической цепиСкачать

Электромеханические аналогии
В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.
Для пружинного маятника мы имеем соотношение, аналогичное (1) :
Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.
Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:
Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.
В самом деле, период колебаний пружинного маятника, как мы знаем, равен:
B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:
Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.
Видео:Колебательный контур. Получение электромагнитных колебаний | Физика 9 класс #45 | ИнфоурокСкачать

Гармонический закон колебаний в контуре
Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».
Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.
Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).
Рис. 10. Положительное направление обхода
Сила тока считается положительной 0)’ alt='(I > 0)’ /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .
Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.
При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0′ alt=’I > 0′ /> , то заряд левой пластины возрастает, и потому 0′ alt=’dot > 0′ /> .
Величины и меняются со временем, но энергия контура остаётся неизменной:
Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):
Подставляя сюда и , получим:
Но сила тока не является функцией, тождественно равной нулю; поэтому
Перепишем это в виде:
Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:
Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:
Мы снова пришли к формуле Томсона.
Гармоническая зависимость заряда от времени в общем случае имеет вид:
Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.
Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :
Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:
Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:
Амплитуда силы тока равна:
Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2 ).
Ток течёт в отрицательном направлении: . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13) .
А теперь посмотрите на рис. 8 . Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!
Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).
Рис. 11. Графики колебаний заряда и тока
Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.
Используя формулу приведения
запишем закон изменения тока (13) в виде:
Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .
Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).
Видео:5.4 Уравнение гармонических колебанийСкачать

Вынужденные электромагнитные колебания
Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.
Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).
Рис. 12. Вынужденные колебания
Если напряжение источника меняется по закону:
то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте .
Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.
📺 Видео
Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать

Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Урок 361. Вынужденные колебания в последовательном колебательном контуреСкачать

Урок 353. Колебательный контурСкачать

Урок 327. Гармонические колебанияСкачать

Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Урок 354. Математическое описание процессов в колебательном контуреСкачать

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Механические и электромагнитные колебанияСкачать

Заряд q конденсатора в идеальном колебательном контуре изменяется по закону q=10 −4 sin - №28438Скачать

Затухающие колебания Лекция 11-1Скачать

Превращение энергии при электромагнитных колебаниях | Физика 11 класс #11 | ИнфоурокСкачать