Уравнение колебаний струны закрепленной на концах (8 видео)

Лекция 2. Вывод уравнения колебания струны

Рассмотрим струну длины l

Струной будем называть тонкую туго натянутую упругую нить.

При построени математической модели колебаний струны будем рассматривать малые колебания, происходящие в одной и той же плоскости. Пусть в состояниии покоя струна расположена вдоль оси Ox на отрезке [0,l] и при колебании каждая точка перемещается перпендикулярно оси (поперечные колебания). Тогда отклонение любой точки струны в произвольный момент времени U есть функция U(x,t) (см. рис.2).

Предположим, что натяжение столь велико, что силой тяжести и сопротивлением при изгибе можно пренебречь. Кроме того, в силу малости колебаний, будем пренебрегать также величинами высшего порядка малости по сравнению с производной U_x.

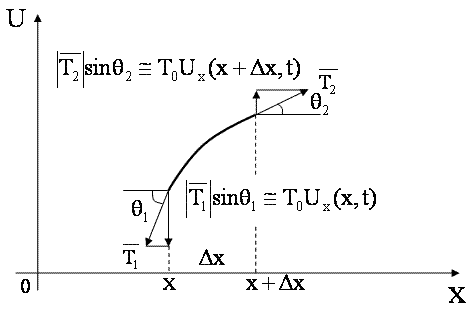
Рис. 3

Выделим малый участок струны (см. рис.3) и рассмотрим силы, действующие на него. Так как струна не сопротивляется изгибу, то ее натяжение направлено по касательной к струне в точке x. Более того, в рамках наших предположений можно считать величину силы натяжения постоянной. В самом деле, длина любого участка струны (величиной U_x 2 можно пренебречь). С ледовательно, в соответствии с законом Гука _.

Пусть ρ ( x )- линейная плотность в точке x , а γ ( x , t )- плотность внешних сил, действующих на струну в момент времени t, и направленных перпендикулярно Ox .

Результирующая сила, действующая на участок струны [ x , x +∆ x ] в направлении перпендикулярном оси OX , равна (см. рис. 3)

При выводе этой формулы учитываем, что при малых колебаниях

По второму закону Ньютона произведение массы на ускорение равно действующей силе mw = F , где w=U_tt, поэтому

ρ ∆ xU_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]+ γ ( x , t ) ∆ x .

Разделим обе части равенства на Δx и устремим Δx к нулю:

ρ ( x ) U_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]/ ∆ x + γ ( x , t ) .

Это уравнение называется уравнением вынужденных колебаний струны. Если струна однородная, то есть ρ ( x )= const , то уравнение (3) обычно записывают в виде

U_tt = a 2 U_xx + f ( x , t ),где a 2 = T ₀/ ρ ; f ( x , t )= γ ( x , t ) / ρ .

В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны

Уравнения (3) и (4) являются одномерными волновыми уравнениями (соответственно, неоднородным и однородным).

Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.

Содержание

Начальные условия и граничные условия.
Вынужденные колебания струны закрепленной на концах. Задача Штурма—Лиувилля
Электронная библиотека
📺 Видео

Начальные условия и граничные условия.

Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за t=0. В результате возникает задача Коши. Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.

Для волнового уравнения U_tt = a 2 U_xx задаются два начальных условия U | _{t =0} = φ ( x ), U_t | _{t =0} = ψ ( x ). Иногда их записывают иначе: U ( x , 0) = φ (х), U_t ( x , 0) = ψ (х). Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие — начальные скорости точек струны. В случае волнового уравнения U_tt = a 2 Δ U на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ , соответственно, будут зависеть от двух или трех переменных.

Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными условиями или краевыми условиями.Для уравнения колебаний струны часто задаются условия U | _{x =0} = 0, U | _{x = l} = 0. Иначе их записывают еще и гак: U (0, t )=0, U ( l , t ) = 0. Эти условия физически означают, что концы струны закреплены (то есть отклонения при х = 0 и при х = l в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, U_x |_х=0= 0 , U_x |_х= _l = 0. Такие условия возникают в следующей задаче.

Пусть концы сруны перемещаются вдоль вертикальных направляющих без трения (см. рис.4).

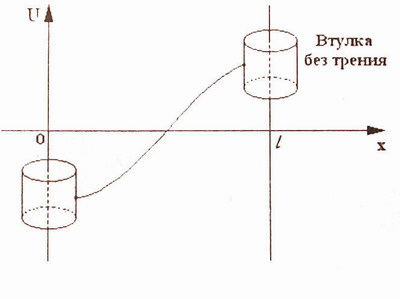
рис.4

Так как вертикальные силы, действующие на левый и правый концы струны, определяютя выражениями T ₀ U_x ( O , t ) и T ₀ U_x (l, t ) (см рис. 2), то записанные выше условия означают, что на концы струны не действуют никакие силы(поэтому такие условия называют еще условиями свободных концов).

Как было уже сказано, волновое уравнение U_tt = a 2 U_xx описывает не только колебания струны, но и другие волновые процессы, к примеру, продольные колебания пружины, продольные колебания стержня, крутильные колебания вала. В этих задачах возникают граничные условия и других видов. Подробно такие задачи мы изучать не будем. Однако приведем основные типы граничных условий. Обычно рассматривают три типа:

Граничные условия (5), (6) и (7) называются однородными, если правые части g₁(t) и g₂(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.

Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных — время. Г раницей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис. 5 ) .

К примеру, граничное условие (однородное) первого рода на плоскости записывается в виде U|_Γ=О, в пространстве U|_Ω=0. Граничное условие второго рода на плоскости имеет вид ,а в пространстве . Конечно, физический смысл этих условий разный для различных задач.

При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)= φ(x), U_t (x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называется первой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.

Видео:Неоднородное уравнение колебания струныСкачать

Вынужденные колебания струны закрепленной на концах. Задача Штурма—Лиувилля

По этой ссылке вы найдёте полный курс лекций по математике:

Рассмотрим колебания однородной струны длины I, закрепленной на концах, под действием внешней силы /(ж, t), рассчитанной на единицу длины. Эта задача приводит к решению уравнения Будем искать решение u(z, t) этой задачи в виде суммы где v(x, t) — решение неоднородного уравнения удовлетворяющее граничным условиям и начальным условиям решение однородного уравнения удовлетворяющее фаничным условиям и начальным условиям Вынужденные колебания струны закрепленной на концах.

Общая схема метода Фурье Задача Штурма—Лиувилля Решение v(x, t) представляет вынужденные колебания струны, т. е. такие колебания, которые совершаются под действием внешней возмущающей силы когда начальные возмущения отсутствуют, а решение представляет свободные колебания струны, т. е. такие колебания, которые происходят только вследствие начальных возмущений.

Метод нахождения свободных колебаний w(x, t) был изложен ранее, так что остается только найти вынужденные колебания решение неоднородного уравнения (5)-(7). Применим метод разложения по собственным функциям, который является одним из мощных методов решения неоднородных линейных уравнений с частными производными.

Основная идея метода состоит в разложении внешней силы f(x, t) в ряд по собственным функциям соответствующей однородной краевой задачи и нахождении откликов uk(x,t) системы на воздействие каждой компоненты /*(*) Хк(х)- Суммируя все такие отклики, получим решение исходной задачи Решение v(x, t) задачи (5)-(7) будем искать в следующем виде: Здесьэш -[-х — собственныефункции однородной краевой задачи, и граничные условия (6) выполняются автоматически.

Чтобы решение v(x, t), определяемое рядом (11), удовлетворяло нулевым начальным условиям (7), достаточно подчинить функции ) условиям Действительно, полагая в (11) t = 0, получим Дифференцируя (11) по t и полагая t = 0, найдем, что . Пользуясь методом вариации постоянных, получим, что решения уравнений (15) при начальных условиях (16) имеют вид где fk<t) определяются по формулам (14).

Подставив найденные выражения для Tt(t) в ряд (11), получим решение t) задачи (5)-(7), если ряд (11) и ряды, полученные из него почленным дифференцированием по х и по t дважды , сходятся равномерно. Как можно показать, такая сходимость рядов будет обеспечена, если функция /(х, t) непрерывна, имеетнепрерывные частные производные по а; до второго порядка включительно и для всех значений t выполняется условие.

Тогда решение и(х, t) исходной задачи (1)-(3) представляется в виде где функции Tk(t) определяютс я по формулам (17), а Пример. Решить смешанную задачу Начальные возмущения отсутствуют, так что мы имеем «чистую- задачу на вынужденные «лебэния однородной струны длины *, закрепленной на концах. Система функций <sin nz) есть ортогональная на (0,*) система собственных функций краевой задачи здесь. Ищем решение задачи (1)-(3) а виде неизвестные функции.

Возможно вам будут полезны данные страницы:

Подставляя в форме ( в уравнение (1), получим отхуда легко усматриваем, что Используя формулу (4), в силу начальных условий (3) получаем откуда Таким образом, для T|(f) имеем Выпишем общее решение уравнения (8) Потребовав выполнение начальных условий (9), находим так что Для n ^ 2 имеем откуда Пользуясь формулой (4), для решения u(x,f) исходной задачи получаем следующее выражение: § 6. Вынужденные колебания струны с подвижными концами Рассмотрим вынужденные колебания однородной струны длины I под действием внешней силы /(х, t), рассчитанной на единицу длины, причем концы струны не закреплены, а двигаются по заданному закону.

Эта задача приводится к решению уравнения при граничных условиях и начальных условиях К решению этой задачи метод Фурье непосредственно неприменим, т. к. граничные условия (2) неоднородны. Однако эта задача легко сводится к задаче с нулевыми (однородными) граничными условиями. Действительно, введем вспомогательную функцию Легко видеть, что Таким образом, функция и(х, t) на концах отрезка /удовлетворяетусловиям(2),авнутри этого отрезка она линейна по х (рис. 8).

Говорят, что функция продолкает граничные условия в интервале Решение задачи (1)43) ищем в виде суммы где v(x, t) — новая неизвестная функция. В силу выбора функции и(х> t) функция ш удовлетворяет нулевым граничным ус- Рис. 8 ловиям и начальным условиям Подставив уравнение (1), получим . или, учитывая выражение для a>(x,t), где Таким образом, при приходим к смешанной задаче с нулевыми граничными условиями для функции найти решение уравнения удовлетворяющее граничным условиям и начальным условиям.

Метод решения таки х задач был изложен ранее. Пример. Решить смешанную задачу ^ Граничные условия неоднородные (концы струны подвижные). Здесь =. Вводим вспомогательную функцию Решение исходной задами будем искать в виде где v(x,t) — новая неизвестная функция. Для нее получаем уравнение граничные условия начальные условия Зада ча (6)-(8) имеет очеандиое решение , и, как ясно из физических соображений, это ее единственное решение.

Тогда по формуле (5) получаем решение u(x,t) исходной задачи §7.

Общая схема метода Фурье Рассмотрим в области дифференциальное уравнение (уравнение колебаний неоднородной струны длины i), где так что уравнение (1) является уравнением гиперболического типа в области Q. Предположим, что и займемся изучением смешанной задачи для уравнения (1) при однородных гранич-ных условиях Вынужденные колебания струны закрепленной на концах Общая схема метода Фурье Задача Штурма—Лиувилля где а, р, у, 6 — некоторые постоянные, причем (Напомним, что задача называется однородной, если, наряду с решением и этой задачи, ее решением является также си, где с — произвольная постоянная.)

Возможны гран ичные условия слото ших типов: (струна с закрепленными концами (рис. 9 а)); (струна со свободными концами (рис.(упруго закрепленные концы (рис. 9 в)). Числа Лю, Л| должны быть положительными, если положение покоя есть положение устойчивого равновесия. Ограничившись для простоты случаем струны с закрепленными концами, приходим к следующей задаче: найти решение и(х, t) уравнения (о удовлетворяющее граничным условиям и начальным условиям (3) ыо Будем решать эту задачу методом Фурье.

1. Ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде произведения Подставляя и(х, t) в форме (4) в уравнение (1), получим или Левая часть последнего равенства зависит только от х, а правая часгь — только от t, и равенство возможно л ишь тогда, когда общая величина отношений (5) будет постоянной.

Обозначим эту постоянную через (-А). Тогда из равенства (5) получим два обыкновенных дифференциальных уравнения Чтобы получитьнетривиальные решения уравнения (1) вида (4), удовлетворяющие граничным условиям (2), необходимо, чтобы функция Х(х) была нетривиальным решением уравнения (7), удовлетворяющим граничным условиям Как мы уже видели, эта задача имеет отличное от тождественного нуля решение не при всяком А.

Задача Штурма—Лиумиим о собственных значениях: найти такие значения параметра X, при которых существуют нетривиальные решения уравнения (7), удовлетворяющие граничным условиям (8), а также сами эти решения. Те значения параметра А, при которых задача (7)-(8) имеет нетривиальное решение, называютс я собственными значениями (числами), а сами эти решения — собственными функциями, огвечающими данному собственному значению.

Совокупность всех собственных значений называется спектром данной задачи. В силу однородности уравнения (7) и граничныхусловий (8) собственные функции определяюгся с точностью до постоянного множителя. Выберем этот множитель так, чтобы (9) Собственные функции, удовлетворяющие условию (9), будем называть нормированными с весом р(х). Установим некоторые общиесвойствасобственныхзначений и собственныхфунк-ций задачи Штурма—Лиувилля. Теорема 3.

Каждому собственному значению с точностью до постоянного множителя отвечает лишь одна собственная функция. М В самом деле, пусть существуют две собственные функции и отвеча- ющие одному и тому же собственному значению Ао, т.е. удовлетворяющие дифференциальному уравнению (7) при одном и том же А = Ао- Так как по предположению Х)(0) = 0, Хг(0) = 0, то определитель Вронского «HxiS Щ решений Х](х) и уравнения (7) в точке ж = 0 обращается в нуль и, следовательно, решения Xi(x) и Х2(х) линейно зависимы.

Теорема 4. Собственные функции, отвечающие различным собственным значениям, ортогональны на отрезке [0, /) свесом р(х), где Хт(х), Хп(х) — собственные функции, соответствующие различным собственным значениям Ато и Предварительно установим одно предложение, имеющее самостоятельный интерес. Введем так называемый оператор Штурма—Лиувшьгя . Будем рассматривать этот оператор на множестве £2[0,J] функций, дважды непрерывно дифференцируемых на |0,<j и удовлетворяющих граничным условиям . Лемма.

Оператор Штурма—Лиувилля (11)

«а (0,1] является симметрическим: самом деле, i Интегрируя по частям , найдем Интегрируя по частям последний интеграл справа и принимая во внимание, что I х Вновь интегрируя по частям второе слагаемое справа и учитывая, что «|Л=0 = и |яв| = О, получим Обратимся к доказательству теоремы. Запишем уравнение (7) в виде и обозначим через L[X оператор, стоящий в левой части (). Это — оператор Штурма—Лиувиллч.

Все собственные значения (7)-(8) действительны В самом деле, допустим, что существует комплексное собственное значение , которому отвечает собственная функция . Тогда комплексно сопряженное число А = а — ip также будет собственным значением, а функция комплексно сопряженная с Х(х), будет соответствующей собственной функцией, поскольку коэффициенты уравнения (7) и граничные условия (8) — действительные. Из условия ортогональности собственных функций, отвечающих различным собстве нным значениям, следует комплексное число А не является собственным значением.

Теорема 6. Если , то все собственные значения задачи (7)-(8) положительные. 4 В самом деле, пусть А* — собственное значение, a Xk(x) — соответствующая собственная функция, нормированная с весом р(х). Тогда справедливо тождество Умножая обе части тождества на интегрируя результат по х от 0 до / и принимая во внимание, что , получим о Интегрируя по частям второе слагаемое справа, придем к равенству Вынужденные колебания струны закрепленной на концах Общая схема метода Фурье.

Задача Штурма—Лиувилля Производная ^ £ О, так как в противном случае Хк(х) = const и из граничных условий (8) мы имели бы Хк(х) = 0, что исключено. Таким образом, правая часть (15) положительна, откуда следует, что все собственные значения А* задачи (7)-(8) поло-жительны. Теорема 7. У задачи (7)-(8) существует счетное множество собственных значений которым отвечают собственные функции Продолжим описание метода Фурье. Обратимся кдифференциальномууравнснию (6).

Егообщеерешсние при имеет вид где Ак, Вк — произвольныепостоянные. Каждая функция Если этот ряд, вместе с рядами, полученными из него двукратным почленнымдиффе-рениированием по а: и по t> сходится равномерно, то его сумма и(х, t) будет решением уравнения (1), удовлетворяющим граничным условиям (2). Для выполнения начальных условий (3) необходимо, чтобы Таким образом, мы пришли к задаче о разложении произвольной функции в ряд Фурье по собственным функциям граничной задачи (7)-(8).

Предполагая, что ряды (17) и (18) сходятся равномерно, можно найти коэффициенты Ак и Вк, умножив обе части равенства (17) и (18) на р(х) Хп(х) и проинтегрировав по х в пределах от 0 до I. Считая функции Хк(х) ортонормированными с весом р(х) на отрезке [О, I], по луч им для коэффициентов Фурье функций по системе следующие выражения:

При нахождении коэффициентов Ап и Вп мы опираемся на теорему разложения Стеклова. Теорема 8. Всякая дважды непрерывно дифференцируемая функция F(x), удовлетворяющая граничным условиям задачи, может быть разложена в абсолютно и равномерно сходящийся ряд по собственным функциям Хк(х) этой задачи, нормированные с весом р(х) собственные функции.

Подставим найденные значения коэффициентов Ап и Вп вряд (16) и, если ряд (16) и ряды, полученные из негодаукратным почленным дифференцированием по х и по t, сходятся равномерно, получим решение и(х, t) смешанной задачи (1)-(3). Замечание. Мы рассмотрели случай простейших граничных условий . Несколько изменяя приведенные выше рассувдения, можно доказать аналогичные свойства собствс шых значений и собствен них функций более обшей однородной краевой задачи

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Электронная библиотека

Здесь мы покажем, как применяются ряды Фурье при решении задачи о колебании струны. Под струной мы понимаем тонкую гибкую нить, не оказывающую сопротивления изгибу.

Рассмотрим струну, которая в начальный момент совмещена с отрезком оси Ох. Будем считать, что концы х = 0 и x = l закреплены на оси Ох. Пусть струна растягивается силами и , приложенными к её концам и направленными вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить самой себе, под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдет дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна станет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.

Сделаем ряд предположений. Во-первых, считаем, что, выводя струну из состояния равновесия, мы придаем ей форму некоторой линии. Поскольку концы струны закреплены на оси Ох, то на функцию U(x) линии надо наложить требования U(0) = U(l) = 0. Во-вторых, будем предполагать, что каждая точка струны совершает только поперечные колебания, перпендикулярные оси Ох. В-третьих, колебания предположим малыми, что квадратами отклонений точек струны от оси Ох можно пренебречь. Кроме того, будем считать, что во все время движения струна будет сохранять пологую (гладкую) форму, это значит, что угол , образуемый касательной к струне с осью Ох, мал, чтобы можно было считать . Наконец, считаем струну однородной, причем массу единицы длины струны в её нерастянутом состоянии считать равной её плотности .

Возьмем какую-либо точку струны, имевшую в начальный момент t = 0 абсциссу х. Так как эта точка будет двигаться перпендикулярно оси Ох, то во время движения её абсцисса х не будет меняться. Ордината её у будет зависеть от времени, а также от того, о какой точке идет речь, а именно от абсциссы х этой точки, т.е. ордината будет функцией от х и t. Эту функцию в дальнейшем будем обозначать через U(x, t). Ясно, что она должна удовлетворять граничным условиям:

и начальным условиям:

первое из (4.10) выражает, что струне придана форма, а второе означает, что точки струны имеют начальные скорости (мы, предположим, что ).

Переведем физическую задачу на язык математики, т.е. выведем дифференциальное уравнение, которому должна удовлетворять искомая функция U(x,t). Для этого выделим на струне элементарный участок, который при t = 0 совпадает с отрезком [x,x+dx] оси Ох. В момент t это будет дуга линии U(x ,t). Длина этой дуги:

пренебрегая (мы сделали допущение, что ), получим: ds = dx (т.е. струна не растягивается). Масса выделенного участка равна: . К этому элементу будут приложены растягивающие его силы. Пусть натяжение в точке х будет равно . Тогда к концам нашего элемента будут приложены силы и .

Они направлены по касательным в этих точках. Обозначим через и соответствующие углы в точках струны (рис. 4.1). Обозначим равнодействующую сил, приложенных к концам элемента, через , а ускорение элемента через . Тогда векторное уравнение движения элемента имеет вид:

Спроектируем это уравнение на ось Ох, находим:

( означает проекцию силы на ось Ох, а – численные значения натяжения в точке, абсцисса которой х).

Поскольку точки струны движутся перпендикулярно оси Ох, то , стало быть . Но

так как . Сопоставляя это с равенством , находим, что . Это значит, что величина натяжения не меняется вдоль струны. Но, так как на концах струны это натяжение есть , вместо F_x, F_x₌_dx будем писать: .

Спроектируем уравнение (4/11) на ось Оу:

Так как , а то (4.13) дает:

Тогда уравнение будет иметь вид:

где . Уравнение (4.14) называется уравнением свободных колебаний струны или волновым уравнением.

Таким образом, механическая задача свелась к чисто математической (получили математическую модель процесса колебания струны): найти такое решение уравнения (4.14), которое удовлетворяет начальным и граничным условиям (4.9) и (4.10). Существуют разные способы решить эту задачу. Один из способов был предложен в XYIII веке Д. Бернулли. Позже, уже в XIX веке, этот способ систематически применялся Фурье для решения целого ряда термодинамических задач, почему он и получил название метода Фурье. Этот способ мы рассмотрим далее. Он требует сначала решения одной важной задачи, которая носит название задачи о собственных значениях и собственных функциях. Однако решим одну вспомогательную задачу: найти функцию U = U(x, t), удовлетворяющую требованиям:

Отличие этой задачи от той, которую нам надо решить, состоит в том, что от искомой функции U(x ,t) мы не требуем, чтобы она удовлетворяла начальным условиям где , но зато требуем, чтобы она имела специальный вид X(x)T(t) и была отличной от тождественного нуля.

Измененная задача решается довольно просто и имеет бесконечное множество решений, из которых удается составить и решение нашей основной задачи.

Итак, пусть имеем первое условие (4.15).

Из него вытекает, существование такой точки , что . Тогда , т.е. . Подставим в граничные условия:

Отсюда видно, что искомая функция X(x) должна удовлетворять условиям:

Подставляя из четвертого условия (4.15.) во второе, получим:

Обратим внимание, на то, что правая часть (4.15) не зависит от . Следовательно, и левая часть от не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного , ибо . Значит, левая (и правая) часть равенства должна быть постоянной величиной. Обозначим ее (пока неизвестную) через .

Допустим, что . Тогда из (4.17) следует . Отсюда и , т.е. должна быть линейной функцией. Подставляя в X(0 )= X(l) = 0, получим:

т.е. , а с ним и , что противоречит допущению первому из (4.15). Таким образом, не существует решения вспомогательной задачи для .

Допустим, что , т.е. , где можно считать положительным. Тогда

Общее решение этого уравнения имеет вид:

Решая эту систему, находим . Это приводит к , что противоречит первому условию (4.15). Итак, неравенство невозможно.

Пусть , т.е. , где . Тогда

Решив это уравнение, получим:

Граничные условия дают: . Заменяя на С, имеем , а второе условие дает . Это возможно лишь при . Значит, для возможны значения , что приводит к следующим выражениям для :

причем при каждом может принять любое (отличное от 0) значение. Заметим, что здесь решена задача о собственных значениях и собственных функциях. Поэтому числа и функции называются соответственно: собственными числами, а функции собственными функциями, которые соответствуют собственным числам (значениям).

Выбрав возможное значение , и подставив в (4/17), получим:

где А и В – произвольные постоянные. Обозначая Т буквой Т_n и полагая , , получаем бесконечное множество решений вспомогательной задачи:

Отметим, что наше уравнение и условия линейны и однородны, т.е. такие, что сумма функций , которая удовлетворяет им, также будет решением. Поэтому функция

при условии сходимости ряда также будет решением. Чтобы функция (4.22) была решением исходной задачи надо подобрать и так, чтобы выполнялись начальные условия (4.10).

Первое условие с (4.10) дает:

Дифференцируя (4.22), получим:

Чтобы удовлетворить соотношению (4.24), надо положить . Соотношение (4.23) говорит, что коэффициенты должны равняться коэффициентам разложения функции , заданной на [0,l], по функциям в ряд Фурье. Поэтому

Таким образом, искомое решение имеет вид

где определяется по (4.25).

1) Полученное решение носит формальный характер, так как мы не исследовали сходимость ряда (4.26). Однако можно показать, что если функция гладкая на [0,l], то ряд сходится и его сумма U(x,t) удовлетворяет исходному уравнению и начальным и краевым условиям.

2) Примененный метод решения задачи обычно называют методом Фурье или методом разделения переменных или методом собственных функций.

Решение (4.22) с учётом , можно записать в виде:

Каждый член этого ряда представляет собой так называемую стоячую волну, при которой точки струны совершают гармоническое колебательное движение с одинаковой фазой , с амплитудой и частотой .

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00