Уравнение колебаний математического маятника для случая малых углов отклонения и его решение

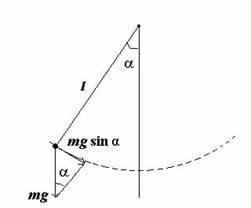
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, движущаяся в одной и той же вертикальной плоскости под действием силы тяжести.

Рассмотрим движение маятника массой т_ и длиной ОМ=_1 (рис. 14.4). На точку М действуют сила тяжести Р и реакция нити N.

Составим дифференциальное уравнение движения точки М в проекции на касательную к ее траектории:

Подставив значения V =/ф и Р= mg, получим

Это дифференциальное уравнение нелинейно и в элементарных функциях не интегрируется. Но при малых углах отклонения маятника от положения равновесия можно считать, что sin ф « ср. Поэтому, положив к 2 = g/l, получим

Это дифференциальное уравнение совпадает по виду с дифференциальным уравнением (14.2) прямолинейных свободных колебаний материальной точки. Его решение по аналогии с равенством (14.6) будет

где А — угловая амплитуда; а — начальная фаза (величины, определяемые по начальным условиям).

Период этих колебаний определим подстановкой значения k-s[g/l в формулу (14.8):

Как видим, период малых колебаний математического маятника не зависит от начальных условий, т. е. малые колебания маятника изохронны. Этот факт был экспериментально установлен еще Галилеем в 1583 г.

Формулы математического маятника

Определение и формулы математического маятника

Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника

Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$

где $alpha $ — начальная фаза колебаний; $_0$ — амплитуда колебаний; $_0$ — циклическая частота.

Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

Период колебаний математического маятника ($T$) в этом случае равен:

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:

Максимальное значение потенциальной энергии математического маятника равно:

Максимальная величина кинетической энергии:

где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m=_0x_m$ — максимальная скорость.

Примеры задач с решением

Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?

Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

Из уравнения (1.1) найдем искомую высоту:

Ответ. $h=frac$

Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit

Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

Выразим из нее ускорение:

Проведем вычисления ускорения силы тяжести:

Ответ. $g=9,87 frac$

Механические гармонические колебания

Рассмотрим так называемый математический маятник — материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.

Второй закон

1643 — 1727

для такого маятника запишется так:

, или

Сравнивая его с дифференциальным уравнением гармонических колебаний (2), увидим, что оно по виду будет совпадать, если sin a заменить на a , что можно сделать при малых a . Следовательно, колебания математического маятника можно считать гармоническими только при малых углах отклонения от положения равновесия.

Итак, гармонические колебания математического маятника описываются уравнением

Сравнивая его с уравнение (2), находим, что циклическая частота собственных колебаний математического маятника

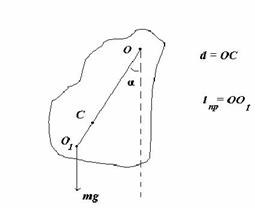
Рассмотрим так называемый физический маятник, то есть реальное физическое тело, совершающее колебания относительно горизонтальной оси O (оси качания), не проходящей через центр инерции тела C.

На рисунке обозначено:

ось качания маятника — неподвижная горизонтальная ось О, не проходящая через центр тяжести тела;

точка подвеса маятника О — пересечение оси качания с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания;

приведенная длина физического маятника L пр — длина математического маятника, имеющего такой же период колебаний;

центр качания физического маятника — О₁.

Согласно второму закону Ньютона, уравнение движения такого маятника запишется следующим образом:

где J — момент инерции маятника относительно точки О.

Видно, что колебания физического маятника также будут гармоническими только при малых углах качания, то есть когда sin a @ a . В этом случае уравнение движения (колебаний) маятника совпадает по виду с дифференциальным уравнением свободных колебаний:

Сравнивая это уравнение с уравнением свободных колебаний, найдем частоту колебаний физического маятника:

Из определения приведенной длины физического маятника найдем, что:

Здесь J_c — момент инерции относительно центра масс тела С.

Центр качания О₁ обладает тем свойством, что, если ось качания провести через О₁, частота колебаний маятника не изменится, а центр качания будет располагаться в точке О. То есть точки О и О₁ обладают свойством взаимозаменяемости. Проверить это утверждение следует следующим образом: необходимо вычислить частоту колебаний маятника, когда ось качания проходит через точки О и О₁ и сравнить эти формулы.

Рассмотрим пружинный маятник (или в общем случае так называемый линейный гармонический осциллятор), то есть материальную точку массой m, совершающую линейные гармонические колебания под действием упругой силы F:

F = — k x (для пружины это — закон Гука).

Второй закон Ньютона для такого маятника запишется так:

, или

Последнее уравнение является уравнением свободных колебаний, откуда сразу находим период колебаний:

💥 Видео