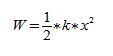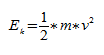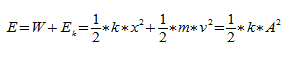Уравнение колебаний координаты пружинного маятника

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

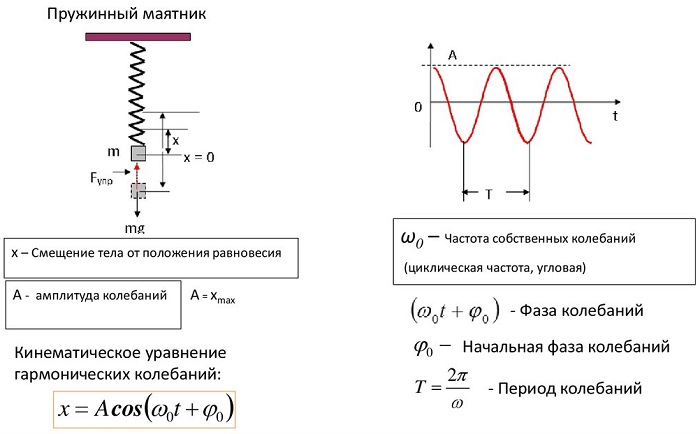
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Видео:Математические и пружинные маятники. 11 класс.Скачать

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :

График функции (1) , выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1 .

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

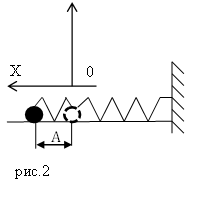
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2 .

Рис. 2. Закон косинуса

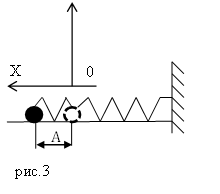
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3 .

Рис. 3. Закон синуса

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1) . Дифференцируем это равенство:

Теперь дифференцируем полученное равенство (4) :

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6) , (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

Видео:5.4 Уравнение гармонических колебанийСкачать

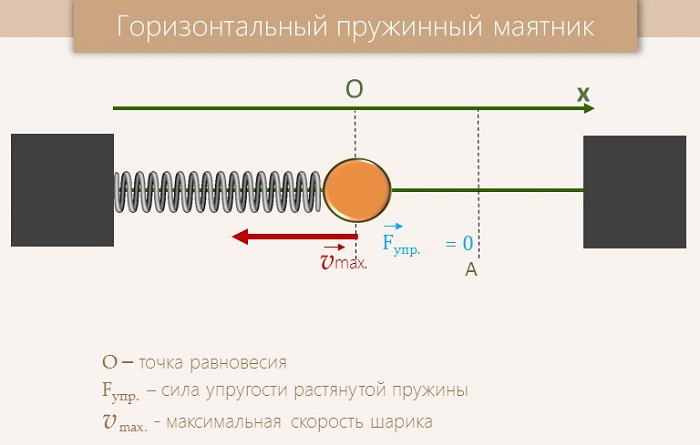
Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

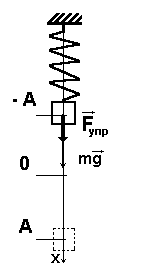
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

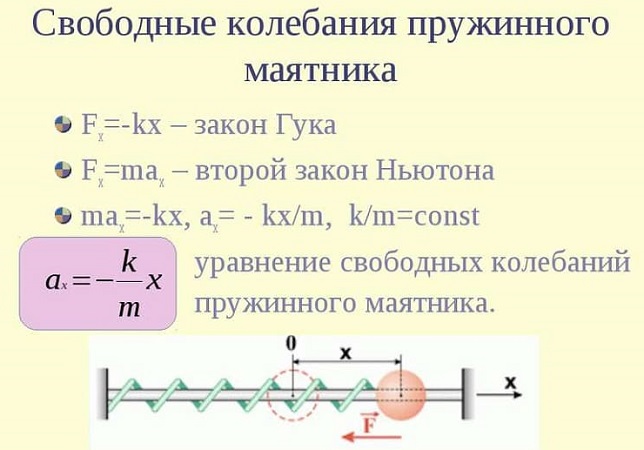
Если 0′ alt=’x>0′ /> (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то 0′ alt=’F_>0′ /> . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

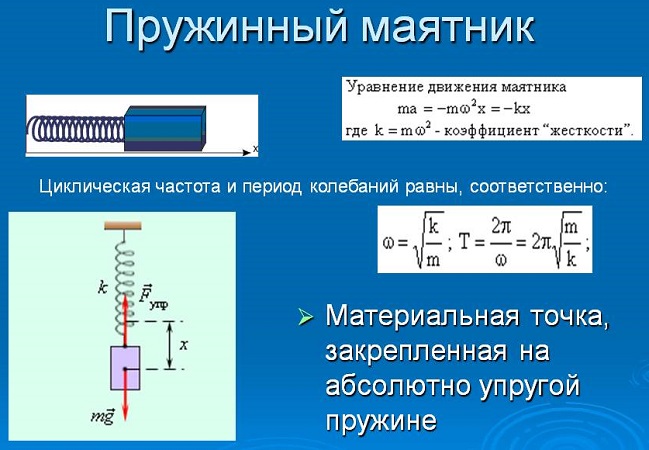
Мы получили уравнение гармонических колебаний вида (6) , в котором

Циклическая частота колебаний пружинного маятника, таким образом, равна:

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10) .

Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5 ). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

Итак, при любом положении маятника имеем:

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11) :

Это — уравнение гармонических колебаний вида (6) , в котором

Следовательно, циклическая частота колебаний математического маятника равна:

Отсюда период колебаний математического маятника:

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Видео:Урок 327. Гармонические колебанияСкачать

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7 .

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Видео:Физика 9 класс. Уравнение механического движения пружинного маятникаСкачать

Формулы пружинного маятника

Видео:Механика. Л 10.1. Колебания. Вывод дифференциального уравнения пружинного маятникаСкачать

Определение и формулы пружинного маятника

Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.

Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Видео:Колебания математического и пружинного маятников. 9 класс.Скачать

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

где $_0=sqrt<frac>>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde=Releft(Acdot exp left(ileft(_0t+varphi right)right)right)left(3right).]

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

Видео:Выполнялка 53.Гармонические колебания.Скачать

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

начальная фаза при этом:

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Видео:Видеоурок по физике "Математический и пружинный маятники"Скачать

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

Закон сохранения энергии для пружинного маятника запишем как:

где $dot=v$ — скорость движения груза; $E_k=frac<m<dot>^2>$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Видео:Период колебаний пружинного маятникаСкачать

Примеры задач с решением

Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac$?

Решение. Сделаем рисунок.

По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:

где $E_$ — потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_$ — кинетическая энергия шарика, в момент прохождения положения равновесия.

Потенциальная энергия равна:

В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:

Из (1.4) выразим искомую величину:

Вычислим начальное (максимальное) смещение груза от положения равновесия:

Ответ. $x_0=1,5$ мм

Задание. Пружинный маятник совершает колебания по закону: $x=A $где $A$ и $omega $ — постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_$. В какой момент времени это произойдет?

Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:

Потенциальную энергию колебаний груза найдем как:

В момент времени, который следует найти $F=F_0$; $E_p=E_$, значит:

Видео:Урок 93 (осн). Исследование пружинного маятникаСкачать

Пружинный маятник — формулы и уравнения нахождения величин

Пружинный маятник — колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.

Приняты следующие обозначения:

k — коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Видео:4 задание ЕГЭ колебания пружинного маятникаСкачать

Виды пружинных маятников

Существует два типа данной системы:

Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.

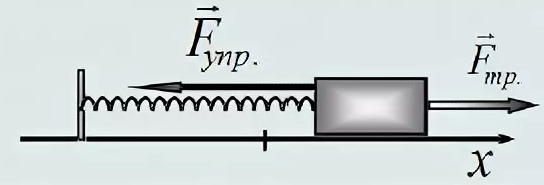
Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

Видео:Математический маятник или откуда формула периодаСкачать

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

где k — коэффициент жесткости пружины (Нм),

Видео:Колебания математического и пружинного маятников. Практическая часть - решение задачи. 9 класс.Скачать

Уравнения колебаний пружинного маятника

Свободные колебания пружинного маятника описываются с помощью гармонического закона.

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = — mw2x(t),

где w — радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Видео:Колебания пружинного маятникаСкачать

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

Факторы, от которых зависит частота:

Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Видео:Механические колебания и все что нужно про них знать. Онлайн школа EXAMhackСкачать

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

Влияние силы трения при расчете не учитывают.

Дифференциальное уравнение гармонических колебаний пружинного маятника

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.