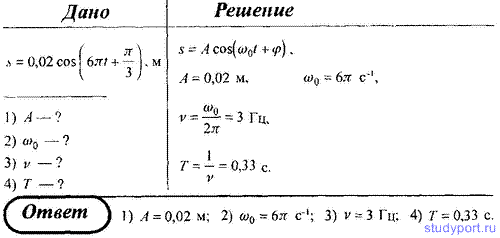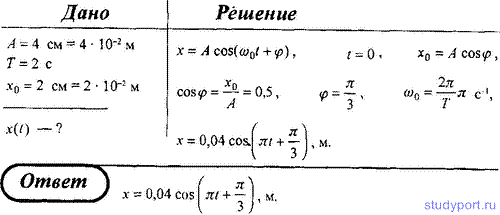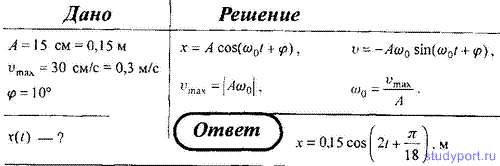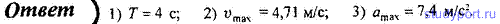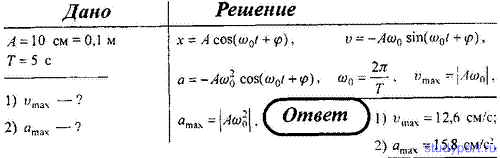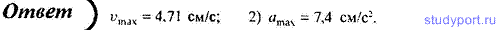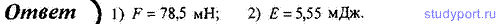Уравнение колебаний груза массой 40 г подвешенного на пружине x 0 3sin20t м жесткость пружины (3 видео)

Содержание

Школе NET
Register
Login
Newsletter
Главный Попко
Груз массой 40 г, подвешенный к пружине, колеблется по закону х = 0,3 sin 20t. Жесткость пружины маятника равна.
Уравнение колебаний груза массой 40 г подвешенного на пружине x 0 3sin20t м жесткость пружины
Контрольная работа по теме Механические колебания и волны 10 класс
1 вариант
2 вариант
3 вариант
4 вариант
5 вариант
Механические и электромагнитные колебания
🌟 Видео

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Школе NET

Register

Do you already have an account? Login

Don’t you have an account yet? Register

Submit to our newsletter to receive exclusive stories delivered to you inbox!

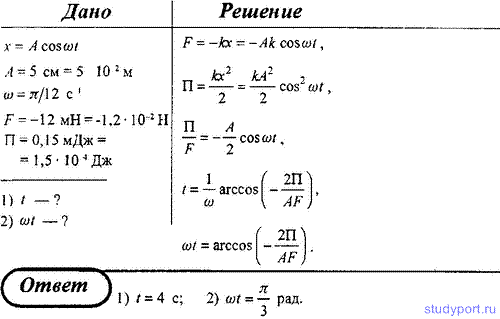
Главная 
Вопросы & Ответы 
Вопрос 13208500

Главный Попко

Видео:9 класс, 34 урок, Колебания математического маятника и груза на пружинеСкачать

Груз массой 40 г, подвешенный к пружине, колеблется по закону х = 0,3 sin 20t. Жесткость пружины маятника равна.

Видео:Подвешенный на пружине груз совершает незатухающие гармонические колебания с некоторой - №23375Скачать

Уравнение колебаний груза массой 40 г подвешенного на пружине x 0 3sin20t м жесткость пружины

Глава 13. Динамика точки.

13.6. Вынужденные колебания.

13.6.1. Дифференциальное уравнение колебательного движения материальной точки дано в виде х + 10x = 1,5 sin (5 t + 0,4). Определить массу точки, если максимальное значение вынуждающей силы F₀ = 60 Н. (Ответ 40)

13.6.2. На тело, которое подвешено к пружине, действует вертикальная вынуждающая сила F = 30 sin 20t. Определить коэффициент динамичности, если угловая частота собственных колебаний тела k = 25 рад/с. (Ответ 2,78)

13.6.3. Дифференциальное уравнение колебательного движения материальной точки имеет вид у + 36у = 50sin(5t + 0,8). Определить коэффициент динамичности. (Ответ 3,27)

13.6.4. Статическое удлинение пружины под действием груза λ = 9,81 см. Определить коэффициент динамичности, если на груз действует вертикальная вынуждающая сила F = 15 sin 5t. (Ответ 1,33)

13.6.5. На тело массой m = 3кг, которое подвешено к пружине, действует вертикальная вынуждающая сила F = 10 sin 5t. Определить коэффициент жесткости пружины, если коэффициент динамичности η = 4. (Ответ 100)

13.6.6. На тело массой m = 50 кг. которое подвешено к пружине, действует вертикальная вынуждающая сила F = 200sin 10t. Определить коэффициент жесткости пружины в к H/м, если амплитуда вынужденных колебаний равна 0,04 м. (Ответ 10)

13.6.7. Дифференциальное уравнение движения вертикальных колебаний тела имеет вид х + 16х = 20 sin (6t + 0,7). Определить коэффициент жесткости пружины, к которой подвешено тело, если максимальное значение вынуждающей силы F_o = 80Н. (Ответ 64)

13.6.8. Дифференциальное уравнение колебательного движения материальной точки дано в виде 5х + 320х = 90 sin 7t. Определить угловую частоту собственных колебаний точки. (Ответ 8)

13.6.9. На тело, которое подвешено к пружине, действует вертикальная вынуждающая сила F = 40 sin 10t. Определить угловую частоту собственных колебаний, если коэффициент динамичности η = 3. (Ответ 12,2)

13.6.10. На тело массой m = 0,5 кг, которое подвешено к пружине с коэффициентом жесткости с = 600 Н/м, действует вертикальная вынуждающая сила F = 25 sin pt. Определить, при какой угловой частоте р вынуждающей силы амплитуда вынужденных колебаний тела будет равна 0,05 м. (Ответ 14,1)

13.6.11. Дифференциальное уравнение колебаний материальной точки дано в виде х + 81х = 12 sin 5t. Определить амплитуду вынужденных колебаний. (Ответ 0,214)

13.6.12. На груз массой m = 0,1 кг, подвешенный на пружине с коэффициентом жесткости с = 0,5 Н/см, действует вынуждающая сила F = 0,3 sin t. Определить амплитуду вынужденных колебаний в мм. (Ответ 6,01)

13.6.13. Груз массой m = 18 кг, подвешенный к пружине с коэффициентом жесткости с = 360 Н/м, совершает вертикальные колебания под действием вертикальной вынуждающей силы F = 36sin 3t. Определить амплитуду вынужденных колебаний. (Ответ 0,182)

13.6.14. Материальная точка массой m = 5 кг совершает колебания согласно уравнению у = 0,4 sin k t + 0,2 sin pt, где угловая частота собственных колебаний k = 20 рад/с, а вынуждающей силы р = 10 рад/с. Определить максимальное значение вынуждающей силы. (Ответ 300)

13.6.15. Дифференциальное уравнение движения вертикальных колебаний тела, подвешенного к пружине с коэффициентом жесткости с = 24 Н/м, имеет вид х + 8х = 1,2 sin(4t + 0,3). Определить максимальное значение вынуждающей силы. (Ответ 3.6)

13.6.16. Дифференциальное уравнение колебательного движения материальной точки массой m = 4 кг дано в виде х + 7х = 0,5 sin(3t + 0,6). Определить максимальное значение вынуждающей силы. (Ответ 2)

13.6.17. Вынужденные колебания материальной точки массой m = 1 кг в случае резонанса заданы графиком функции х = x(t). Определить максимальное значение действующей на точку вынуждающей силы F = F₀ sin pt. (Ответ 1,26)

13.6.18. Тело массой m = 0,5 кг подвешено к концу пружины с коэффициентом жесткости с = 200 Н/м и совершает вынужденные колебания под действием вынуждающей силы F = 15 sin pt Определить угловую частоту вынуждающей силы, при которой наступит резонанс. (Ответ 20)

13.6.19. Определить амплитуду вынужденных колебаний материальной точки, если дифференциальное уравнение ее движения имеет вид х + 6х + 30х = 4 sin 2t. (Ответ 0,140)

13.6.20. Определить коэффициент динамичности, если дифференциальное уравнение вынужденных колебаний точки у + 8у + 250у = 6 sin 10t (Ответ 1,47)

13.6.21. На тело массой m = 10 кг, которое подвешено к пружине с коэффициентом жесткости с = 150 Н/м, действуют вертикальная вынуждающая сила F = 10 sin pt и сила сопротивления R = -8v. Определить максимальную амплитуду установившихся вынужденных колебаний, которую можно достичь, изменяя значения угловой частоты вынуждающей силы. (Ответ 0,324)

13.6.22. Тело массой m = 5 кг подвешено к пружине с коэффициентом жесткости с = 50 Н/м. Сила сопротивления движению R = -4v. Определить, при какой угловой частоте вертикальной вынуждающей силы коэффициент динамичности будет максимальным. (Ответ 3,11)

13.6.23. Дифференциальное уравнение колебательного движения материальной точки массой m = 12 кг имеет вид у + 8у + 60у = 15 sin 3t. Сила сопротивления движению точки R = — ηy. Определить коэффициент η. (Ответ 96)

13.6.24. Дифференциальное уравнение колебательного движения материальной точки массой m = 3 кг имеет вид х + 4х + 30х = 15 sin 8t. Определить максимальное значение вынуждающей силы. (Ответ 45)

13.6.25. Тело массой m = 5 кг подвешено к пружине. Определить коэффициент жесткости пружины, если дифференциальное уравнение прямолинейного поступательного движения тела имеет вид x + 6x + 40x = 5 sin 15t. (Ответ 200)

Видео:Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой x0. Что - №23311Скачать

Контрольная работа по теме Механические колебания и волны 10 класс

Контрольная работа по теме Механические колебания и волны для учащихся 10 класса с ответами. Контрольная работа состоит из 5 вариантов, в каждом по 8 заданий.

Видео:Груз, подвешенный на пружине, совершает вынужденные гармонические колебания под действием - №23467Скачать

1 вариант

A1. Тело совершает гармонические колебания по закону х = 0,2sin(4πt). Определите амплитуду колебаний.

1) 2 см
2) 20 см
3) 2 м
4) 5 м

А2. На рисунке представлена зависимость координаты центра шара, подвешенного на пружине, от времени.

Частота колебаний равна

1) 0,12 Гц
2) 0,25 Гц
3) 0,5 Гц
4) 4 Гц

А3. На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени.

В момент времени t = 1 с кинетическая энергия маятника равна

1) 0 Дж
2) 10 Дж
3) 20 Дж
4) 40 Дж

А4. На рисунке представлен график зависимости амплитуды А вынужденных колебаний от частоты v вынуждающей силы.

Резонанс происходит при частоте

1) 0 Гц
2) 10 Гц
3) 20 Гц
4) 30 Гц

А5. Волна с частотой 4 Гц распространяется по шнуру со скоростью 8 м/с. Длина волны равна

1) 0,5 м
2) 2 м
3) 32 м
4) для решения не хватает данных

B1. Груз массой 0,08 кг, подвешенный на пружине, совершает свободные гармонические колебания. Какой массы новый груз нужно подвесить вместо первого, чтобы частота колебаний уменьшилась в 2 раза?

В2. Тело массой 5 кг совершает гармонические колебания с амплитудой 10 см. Максимальная кинетическая энергия колеблющегося тела равна 2,5 Дж. Определите период колебаний.

C1. Математический маятник с длиной нити 24 см находится в лифте, который движется с ускорением 2 м/с 2 , направленным вверх. Рассчитайте период колебаний маятника.

Видео:Колебания математического и пружинного маятников. Практическая часть - решение задачи. 9 класс.Скачать

2 вариант

A1. Координата математического маятника изменяется по закону х = 10sin(20t + 5). В соответствии с этой формулой циклическая частота колебаний равна

1) 5 с -1
2) 20 с -1
3) 10 с -1
4) 25 с -1

А2. На рисунке представлена зависимость координаты центра шара, подвешенного на пружине, от времени.

Амплитуда колебаний равна

1) 10 см
2) 20 см
3) -10 см
4) -20 см

А3. На рисунке представлен график изменения со временем кинетической энергии ребенка, качающегося на качелях.

В момент, соответствующий точке А на графике, его полная механическая энергия равна

1) 40 Дж
2) 80 Дж
3) 120 Дж
4) 160 Дж

А4. На рисунке представлен график зависимости амплитуды А вынужденных колебаний от частоты v внешней силы.

При резонансе амплитуда колебаний равна

1) 1 см
2) 2 см
3) 4 см
4) 5 см

А5. Волна частотой 3 Гц распространяется в среде со скоростью 6 м/с. Длина волны равна

1) 1 м
2) 2 м
3) 0,5 м
4) 18 м

B1. Тело массой 100 г совершает колебания на пружине с амплитудой 5 см. Максимальное значение модуля скорости этого тела равно 5 м/с. Определите частоту колебаний.

В2. На каком расстоянии от корабля находится айсберг, если посланный гидролокатором ультразвуковой сигнал, имеющий скорость 1500 м/с, вернулся назад через 0,4 с?

C1. Математический маятник на поверхности Земли имеет период колебаний 2,4 с. Определите период колебаний этого же маятника на поверхности планеты, радиус которой в 50 раз меньше земного радиуса, а плотность в 2 раза больше плотности Земли.

Видео:Физика.Узнать за 2 минуты.Основные понятия.Что такое жёсткость пружиныСкачать

3 вариант

A1. Тело совершает гармонические колебания по закону х = 0,2sin(4πt). Определите частоту колебаний.

1) 0,5 Гц
2) 2 Гц
3) π Гц
4) 2π Гц

А2. На рисунке представлена зависимость координаты центра шара, подвешенного на пружине, от времени.

Период колебаний равен

1) 2 с
2) 4 с
3) 6 с
4) 10 с

В момент, соответствующий точке А на графике, его потенциальная энергия, отсчитанная от положения равновесия качелей, равна

1) 40 Дж
2) 80 Дж
3) 100 Дж
4) 120 Дж

При резонансе амплитуда колебаний равна

1) 1 см
2) 4 см
3) 6 см
4) 10 см

А5. Волна с периодом колебаний 0,5 с распространяется со скоростью 20 м/с. Длина волны равна

1) 10 м
2) 40 м
3) 0,025 м
4) 5 м

B1. Груз массой 0,16 кг, подвешенный на пружине, совершает свободные гармонические колебания. Какой массы новый груз нужно подвесить вместо первого, чтобы частота колебаний увеличилась в 2 раза?

В2. Амплитуда колебаний пружинного маятника 5 см, масса груза 400 г. Максимальная кинетическая энергия груза равна 0,05 Дж. Определите собственную частоту колебательной системы.

C1. Период колебаний математического маятника в неподвижном лифте 1 с. С каким ускорением, направленным вниз, движется лифт, если период колебаний маятника стал 1,1 с?

Видео:Груз массой 0,16 кг, подвешенный на пружине, совершает свободные вертикальные гармонические - №34228Скачать

4 вариант

A1. Зависимость координаты колеблющейся материальной точки от времени имеет вид х = 0,05cos(40πt + π/6) . Определите период колебаний.

1) 1 с
2) 0,5 с
3) 0,1 с
4) 0,05 с

А2. На рисунке показан график колебаний одной из точек струны.

Согласно графику, частота этих колебаний равна

1) 0,12 Гц
2) 0,25 Гц
3) 0,5 Гц
4) 4 Гц

В момент времени t = 2 с полная механическая энергия маятника равна

1) 0 Дж
2) 8 Дж
3) 16 Дж
4) 32 Дж

А4. Груз, прикрепленный к пружине жесткостью 40 Н/м, совершает вынужденные колебания. Зависимость амплитуды этих колебаний от частоты воздействия вынуждающей силы представлена на рисунке. Определите полную энергию колебаний груза при резонансе.

1) 10 -1 Дж
2) 5 · 10 -2 Дж
3) 1,25 · 10 -2 Дж
4) 2 · 10 -3 Дж

А5. Частота колебаний струны равна 500 Гц. Скорость звука в воздухе 340 м/с. Длина звуковой волны равна

1) 68 м
2) 340 м
3) 170 м
4) 0,68 м

В1. Груз массой 2 кг совершает колебания с циклической частотой 5 Гц. Амплитуда колебаний 10 см. Какова максимальная скорость груза?

В2. Ультразвуковой сигнал с частотой 50 кГц возвратился после отражения от дна моря на глубине 150 м через 0,2 с. Какова длина ультразвуковой волны?

C1. Середина нити математического маятника наталкивается на гвоздь каждый раз, когда маятник проходит положение равновесия справа налево. Найдите длину нити, если период колебаний такого маятника 2,41 с.

Видео:Физика. Проверка независимости периода колебаний груза, подвешенного к ленте, от массы грузаСкачать

5 вариант

A1. Зависимость координаты колеблющейся материальной точки от времени имеет вид х = 0,05cos(40πt + π/6). Определите частоту колебаний ускорения.

1) 0,5 Гц
2) 20 Гц
3) 20π Гц
4) 40π Гц

А2. На рисунке показан график колебаний одной из точек струны.

Согласно графику, амплитуда колебаний равна

1) 0,1 см
2) 0,2 см
3) 0,4 см
4) 4 см

В момент времени t = 2 с кинетическая энергия маятника равна

1) 0 Дж
2) 8 Дж
3) 16 Дж
4) 32 Дж

Энергия колебаний груза при частоте 4 Гц равна

1) 8 · 10 -3 Дж
2) 1,6 · 10 -3 Дж
3) 0,5 · 10 -3 Дж
4) 10 -3 Дж

А5. Мимо рыбака, сидящего на пристани, прошло 5 гребней волны за 10 с. Каков период колебаний поплавка на волнах?

1) 5 с
2) 50 с
3) 2 с
4) 0,5 с

B1. Груз, подвешенный на легкой пружине жесткостью 100 Н/м, совершает свободные гармонические колебания. Какой должна быть жесткость пружины, чтобы частота колебаний этого же груза увеличилась в 4 раза?

В2. Максимальная кинетическая энергия материальной точки массой 10 г, совершающей гармонические колебания с периодом 2 с, равна 100 мкДж. С какой амплитудой происходят колебания?

C1. Математический маятник длиной 10 см совершает колебания вблизи вертикальной стенки, в которую на расстоянии 6,4 см под точкой подвеса вбит гвоздь. Определите период колебаний такого маятника.

Ответы на контрольную работу по теме Механические колебания и волны 10 класс
1 вариант
А1-2
А2-2
А3-3
А4-2
А5-2
В1. 0,32 кг
В2. 0,628 с
С1. 0,89 с
2 вариант
А1-2
А2-1
А3-4
А4-4
А5-2
В1. 15,92 Гц
В2. 300 м
С1. 12 с
3 вариант
А1-2
А2-2
А3-1
А4-4
А5-1
В1. 0,04 кг
В2. 10 рад/с
С1. 1,74 м/с 2
4 вариант
А1-4
А2-2
А3-3
А4-2
А5-4
В1. 0,5 м/с
В2. 0,03 м
С1. 2 м
5 вариант
А1-2
А2-2
А3-1
А4-1
А5-3
В1. 1600 Н/м
В2. 4,5 см
С1. 0,5 с

Видео:Физика. 7 класс. Лабораторная работа. Определение жёсткости пружиныСкачать

Механические и электромагнитные колебания

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

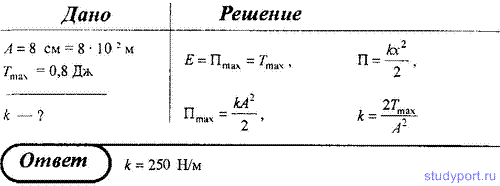
19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с -1 . Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.