Уравнение колебаний физического маятника массой 0 2 кг и моментом инерции

При решении уравнений вращательного или колебательного (осциллирующего) движения необходимо знать момент инерции рассматриваемой системы. Данная статья посвящена изучению различного рода маятников и моменту инерции, которым они характеризуются.

Видео:9. Колебания физического маятникаСкачать

Понятие о маятнике. Виды

Перед тем как приводить определение момента инерции маятника, необходимо рассмотреть, что собой представляет этот прибор. В физике под ним понимают абсолютно любую систему, которая может совершать колебания или вращение вокруг некоторой точки или оси под действием гравитационного поля, то есть силы тяжести. Это определение предполагает, что маятник в обязательном порядке должен обладать конечной массой, при этом центр масс системы не должен находиться в точке, через которую проходит ось вращения.

Существуют различные виды маятников. В данной статье рассмотрим только 3 из них:

• математический, или простой;
• физический (на примере однородного стержня);
• маятник Обербека.

Первые два являются маятниками колебательного типа, третий — вращательного.

Видео:ЛР 1.05 Изучение колебаний физического маятникаСкачать

Вращение и момент инерции

Когда тело с некоторой массой начинает вращаться вокруг оси, то его движение принято описывать следующим уравнением:

Здесь M — это суммарный, или результирующий, момент всех внешних сил, которые действуют на систему, I — ее момент инерции и α — угловое ускорение.

Момент силы M по определению — это величина, равная произведению действующей силы на плечо, которое равно расстоянию от точки приложенной силы до оси вращения.

Момент инерции — величина, характеризующая инерционные свойства системы, то есть насколько быстро ее можно раскрутить, прилагая некоторый момент M. Также I характеризует запасенную вращающейся системой кинетическую энергию. Момент инерции I для материальной точки (воображаемый объект, масса которого сосредоточена в бесконечно малом объеме пространства), совершающей круговое движение на расстоянии от оси r, можно вычислить по следующей формуле:

В общем же случае при определении I для тела произвольной формы следует пользоваться такими выражениями:

Первое равенство применяется при дискретном расположении масс в системе, второе — при непрерывном.

Из этих выражений видно, что I является функцией расстояния до оси вращения и распределения массы в системе относительно этой оси и не зависит ни от прикладываемых моментов сил M, ни от скорости вращения ω.

Видео:Механика. Л 10.2. Колебания. Вывод дифф уравнений колебаний математического и физического маятниковСкачать

Математический (простой) маятник

Поскольку этот вид колебательной системы является самым простым, то рассмотрим его подробнее. Маятник математический представляет собой материальную точку, которая подвешена на невесомой и нерастяжимой нити. Если эту точку отклонить слегка от положения равновесия, а затем отпустить, то она начнет совершать колебания. Также предполагается, что не существует сил трения в точке закрепления нити, и пренебрегают сопротивлением воздуха.

Как понятно из описания выше, математический маятник представляет собой идеальный случай, который не реализуется на практике. Тем не менее его изучение позволяет получить некоторые важные выводы для рассматриваемого типа движения.

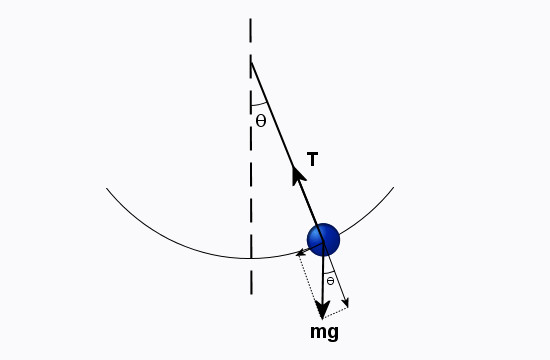
Ниже на рисунке представлен этот маятник, а также обозначены действующие в системе силы при его колебании.

Применяя к нему уравнение движения, получаем следующее равенство:

=> -m*g*sin(θ)*L = m*L 2 *d 2 θ/dt 2 , откуда:

L *d 2 θ/dt 2 + g*sin(θ) = 0.

Поясним некоторые моменты: момент силы от натяжения нити T (см. рис.) равен нулю, поскольку она действует непосредственно на ось; момент от силы тяжести взят со знаком минус, поскольку он направлен по часовой стрелке; L — длина нити; угловое ускорение α по определению является второй производной от угла поворота по времени либо первой производной по времени от угловой скорости ω; формула момента инерции маятника этого типа совпадает с таковой для материальной точки с массой m, находящейся от оси вращения на расстоянии L.

Полученное выше выражение можно упростить, если принять приближение: sin(θ)≈θ. Оно справедливо, когда углы колебания являются небольшими (до θ=10 o ошибка не превышает 0,5 %). В этом случае получаем:

Мы получили классическое дифференциальное уравнение (диф. ур.) второго порядка. Его решением является функция синуса:

Здесь A и θ₀ — амплитуда колебаний и начальный угол отклонения от равновесия, соответственно. Если это решение подставить в диф. ур. выше, то можно получить угловую скорость и период колебаний:

Мы получили удивительный результат: период колебаний математического маятника не зависит от начальных условий (A и θ₀), а также от массы m.

Поведение математического маятника впервые начал изучать Галилей. Впоследствии Гюйгенс показал возможность использования полученной формулы для определения ускорения свободного падения Земли.

Видео:Колебания. Физический маятник. Период и частота колебаний физического маятника.Скачать

Физический маятник общего типа

Этот прибор представляет собой твердое тело произвольной формы (его масса может быть неравномерно распределена по его объему), которое совершает колебания относительно горизонтальной оси, не проходящей через центр масс тела.

При решении уравнения движения этого прибора рассматривают идеальный объект, масса которого сосредоточена в его центре тяжести. Такое предположение приводит к следующей формуле для периода его колебания:

Здесь h — расстояние от центра тяжести до оси вращения O, I_o — момент инерции физического маятника. Заметим, что если для расчета момента силы тяжести можно воспользоваться свойством аддитивности этой величины и свести сумму всех моментов к одному, приложенному к центру тяжести, то для вычисления момента инерции I_o так поступать нельзя, его следует рассчитывать с использованием общих формул, которые были приведены ранее.

Видео:Момент инерцииСкачать

Колеблющийся стержень и его момент инерции

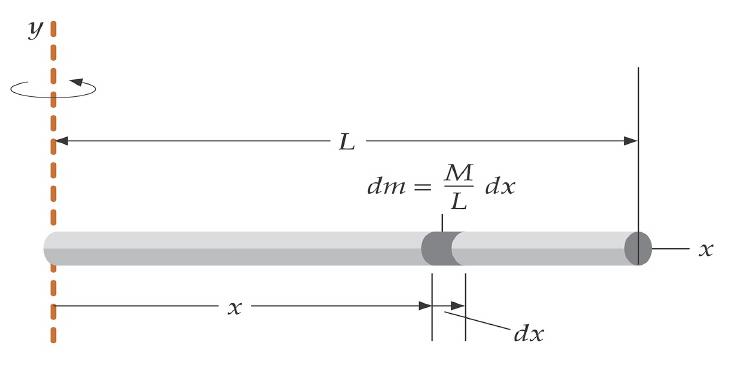
Представим себе, что имеется твердый стержень массой m и длиной L, который подвешен к одному из концов вертикально. Эта конструкция способна совершать колебания под действием земного притяжения.

Если применить интегрирование относительно оси к такому стержню, то можно получить, что момент инерции маятника физического указанной конструкции будет равен:

Тогда его период колебаний будет равен:

Видео:Физический маятникСкачать

Маятник Обербека

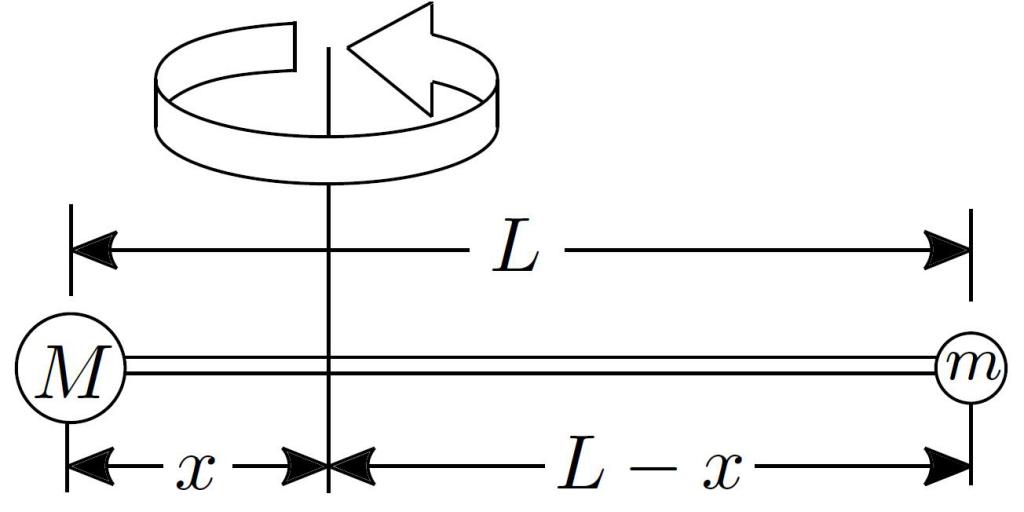
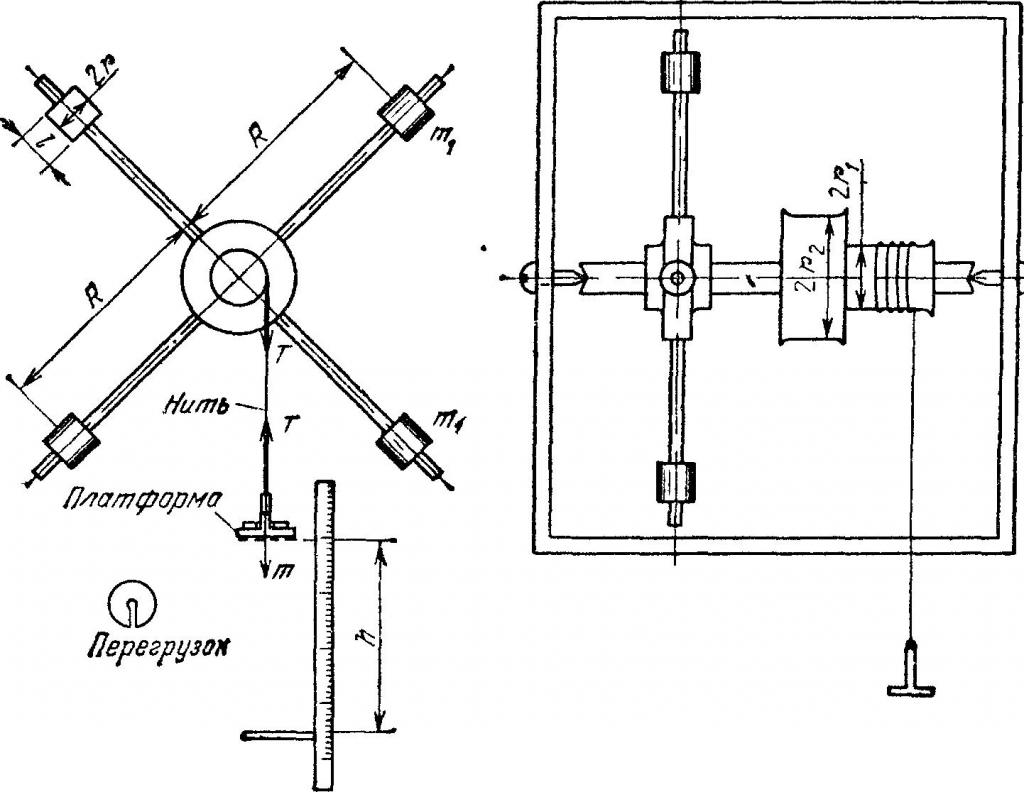
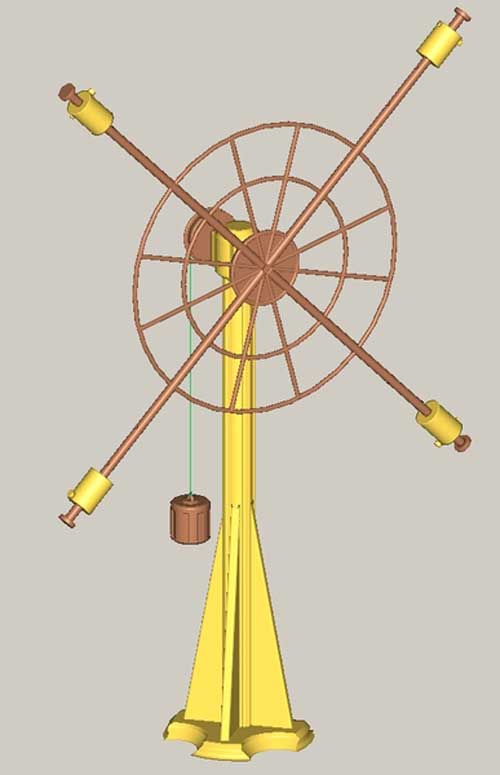
На рисунке ниже приведен этот вид маятника.

Из рисунка видно, если подвесить груз к нити, то 4 стержня с грузами начинают вращаться с некоторым угловым ускорением.

Маятник Обербека используется для проведения лабораторных работ по физике с целью проверки уравнения вращательного движения.

Видео:физический маятникСкачать

Определение момента инерции маятника Обербека

Для решения этой задачи необходимо сделать важное приближение: вес стержней и дисков, к которым подвешивается на нити перегрузок, является пренебрежимо малым по сравнению с весом одного груза m. Учитывая, что размер грузов намного меньше их расстояния до оси вращения, можно воспользоваться формулой для момента инерции материальной точки. Поскольку грузов 4 и все они имеют одинаковую массу, но расположены на разных расстояниях от оси, то получаем следующую формулу для момента инерции маятника Обербека:

Поскольку этот маятник позволяет регулировать положение каждого груза на стержне, то его момент инерции может изменяться.

Видео:Изучение колебаний физического маятника и проверка теоремы Гюйгенса ШтейнераСкачать

Колебания механических систем

3. Колебания механических систем

3.1. Физический маятник

3.1.1. Физический маятник представляет собой однородный стержень длины l = 2 м. Колебания происходят вокруг горизонтальной оси, перпендикулярной стержню и проходящей через его верхний конец.

1. Момент инерции стержня относительно горизонтальной оси колебаний определится как

. (1)

2. Период малых колебаний физического маятника при расстоянии от центра масс до оси колебаний d = l/2, определится посредствам уравнения

. (2)

3.1.2. Физический маятник представляет собой тонкий стержень длиной l = 2 ми массой m0 = 1 кг, на концах которого закреплены свинцовые шарики массами m1 = m2 = 0,5 кг. Маятник совершает малые колебания вокруг оси, проходящей через середину стержня перпендикулярно его оси. Определить период колебаний.

1. Период колебаний физического маятника определяется уравнением

, (1)

где Jz — момент инерции маятника относительно оси колебаний z, M — масса маятника, lС — расстояние от центра масс маятника до оси.

2. Маятник состоит из двух точечных масс m1 и m2 и массы стержня m0, поэтому его суммарный момент инерции определится как

. (2)

3. Поскольку маятник симметричен, то ось вращения будет проходить через центр масс, т. е. lC = l/2, поэтому период маятника определится следующим уравнением

. (3)

3.1.3. В условиях предыдущей задачи массы шаров равны m1 = 0,3 кг, m2 = 0,6 кг. Определить период колебаний стержня, длина и масса которого остались неизменными.

1. В этом случае момент инерции стержня с шарами определится посредствам уравнения

. (1)

2. Так как на концах стержня закреплены шары разной массы, то ось z, вокруг которой происходят колебания, не будет совпадать с центром масс. Определим положение центра масс маятника

, (2)

, (3)

. (4)

3. Период колебаний маятника

. (5)

3.1.4. Однородный диск радиусом R = 30см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Определите период колебаний этого физического маятника.

1. В данном случае расстояние между осью, относительно которой происходят колебания и центром масс диска равно радиусу диска, т. е. lC = R.

2. Момент инерции диска относительно оси, проходящий через образующую диска определяется как

. (1)

3. Период колебаний такого физического маятника будет равен

. (2)

3.1.5. На концах невесомого тонкого стержня длиной l = 1 м укреплены одинаковые грузы. Стержень совместно с грузами колеблется вокруг вертикальной оси, проходящей через точку, удалённую на расстояние d = 0,25 м от одного из грузов. Определить период колебаний маятника и его приведённую длину.

1. Определим расстояние между центром масс и осью z, вокруг которой происходят колебания

. (2)

2. Определим момент инерции маятника

. (3)

3. Период колебаний данного физического маятника

. (4)

4. Приведённая длина маятника определится как

. (5)

3.1.6. На концах невесомого тонкого стержня длиной l = 0,3 м укреплены одинаковые точечные грузы. Стержень совместно с грузами колеблется вокруг горизонтальной оси, проходящей через точку, удалённую на расстояние d = 0,1 м от одного из концов стержня. Определить период колебаний маятника и его приведённую длину.

1. В отличие от предыдущей задачи, где колебания происходили в плоскости перпендикулярной вектору силы тяжести, т. е. при движении системы потенциальная энергия не изменялась, в данном случае изменение относительного положения грузов будет сопровождаться изменением потенциальной энергии системы. Момент инерции, при этом, определится как

. (1)

2. Период колебаний такого физического маятника, при учёте того, что lC = l/4, будет определяться уравнением (4) предыдущей задачи

. (2)

3. Приведённая длина маятника

. (3)

3.1.7. На невесомом стержне длиной l = 0,3 м закреплены два одинаковых шарика: один в середине стержня, а второй — на одном из его концов. Система тел колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить период колебаний и приведённую длину этого физического маятника.

1. Определим положение центра масс данной механической системы

. (1)

2. Найдём далее момент инерции маятника относительно горизонтальной оси вращения

. (2)

3. Приведённая длина физического маятника, с учётом того, что расстояние между центром масс маятника и осью, вокруг которой происходят колебания d = 3l/4

. (4)

4. Период колебаний маятника

. (5)

3.1.8. Физический маятник представляет собой систему трёх точечных грузов, соединённых невесомыми стержнями одинаковой длины l = 0,3 м колеблется вокруг горизонтальной оси, проходящей перпендикулярно плоскости чертежа через общую точку О стержневой системы. Определить период колебаний маятника.

1. Определим положение центра масс относительно оси колебаний, проходящих через точку О

, (1)

. (2)

2. Расстояние между центром масс и осью колебаний составит

. (3)

3. Момент инерции анализируемой колебательной системы относительно оси, проходящей через точку О перпендикулярно плоскости чертежа

. (4)

4. Период колебаний маятника

. (5)

3.1.9. Тонкий обруч радиусом R = 0,3 м колеблется вокруг вбитого горизонтально в стену гвоздя, так что плоскость колебания параллельна стене. Определить период колебаний такого физического маятника.

1. В данном случае центр масс обруча не совпадает с осью колебаний, для определения момента инерции относительно оси колебаний х, перпендикулярной плоскости чертежа необходимо воспользоваться теоремой Гюйгенса — Штейнера

. (1)

2. Период колебаний обруча

. (2)

3.1.10. Однородный диск радиусом R = 0,3 м колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Определить период колебаний.

1. Так же как и в предыдущей задаче, центр масс диска не совпадает с положением оси х, относительно которой колеблется физический маятник. Для определения момента инерции диска относительно оси х воспользуемся теоремой Гюйгенса — Штейнера

. (3)

2. Период колебаний маятника с учётом того, что d = R, определится посредствам следующего уравнения

. (4)

3.1.11. Диск радиусом R = 0,24 м колеблется вокруг горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведённую длину и период колебаний маятника.

1. По методике, использованной в предыдущих задачах определим момент инерции диска относительно горизонтальной оси х, которая разнесена с осью колебаний на расстояние d = R

. (2)

2. Приведённая длина физического маятника

. (3)

3. Период колебаний

. (4)

3.1.12. Математический маятник длиной l1 = 0,4 м и физический маятник в виде тонкого прямоугольного стержня длиной l2 = 0,6 м синхронно колеблются около одной горизонтальной оси. Определить расстояние d между центром масс стержня и осью его колебаний.

1. Поскольку колебания математического и физического маятников синхронные, то периоды будут одинаковыми

.

3.1.13. Физический маятник представляет собой однородный диск радиусом r = 0,4 м, горизонтальная ось колебаний которого проходит на расстоянии d = r/4 от центра масс диска. Определить период малых колебаний диска.

1. Момент инерции диска относительно оси, проходящей центр масс, определяется уравнением

. (1)

2. Момент инерции относительно параллельной оси, отстоящей на расстоянии d, определим с помощью теоремы Гюйгенса — Штейнера

. (2)

3. Период малых колебаний этого физического маятника запишется следующим образом

. (3)

3.2. Свободные колебания механических систем

3.2.1. Определить частоту малых колебаний тонкого однородного стержня массой m = 1 кг длиной l = 1 м вокруг горизонтальной оси, проходящей через точку О, если противоположный конец стержня присоединён к пружине жёсткости k = 100 Н/м. В статическом положении стержень вертикален и пружина не деформирована.

1. Момент инерции стержня относительно оси колебаний

. (1)

2. Рассматриваемая конструкция физического маятника в соответствие с уравнением (1) имеет следующее значение приведённой массы

(2)

3. Циклическая частота колебаний стержня при условии равенства расстояния от оси колебаний до центра масс d = l/2 определится уравнением

. (3)

4. Циклическая частота собственных колебаний стержня, один конец которого присоединён к пружине жёсткостью k

. (4)

5. Период собственных малых колебаний физического маятника

. (4)

3.2.2. Однородный стержень массой m = 1 кг совершает колебания вокруг горизонтальной оси, проходящей через точку О, свободный конец стержня соединён с вертикальной пружиной жёсткости k = 10 Н/м. Определить период малых колебаний физического маятника.

1. Физический маятник в данном случае можно рассматривать как часть массы стержня подвешенной к вертикальной пружине. Присоединённую к пружине массу определим их уравнения момента инерции стержня относительно горизонтальной оси, проходящей через точку О перпендикулярно плоскости чертежа

. (1)

2. Период колебаний в этом случае запишется как

. (2)

3.2.3. Найти циклическую частоту собственных малых свободных горизонтальных колебаний однородного диска массой m = 0,33 кг, соединённого с пружиной жёсткостью k = 50 Н/м. Качение диска по горизонтальной плоскости происходит без проскальзывания.

1. Если в качестве обобщённой координаты принять горизонтальное перемещение диска х, то уравнение его кинетической энергии можно представить в виде суммы энергии поступательного движения и энергии вращения

. (1)

2. Момент инерции диска относительно оси z, перпендикулярной плоскости чертежа и проходящей через точку крепления пружины к диску

. (2)

3. Подставим уравнение (2) в уравнение (1)

, (3)

приведённая масса, при этом, равна .

4. Определим частоту собственных колебаний

. (4)

3.2.4. Определить собственную частоту колебаний системы, состоящей из упруго закреплённой горизонтальной рейки А, которая лежит на подпружиненном цилиндре В и катке С. Массы рейки m1 = 1 кг и цилиндра m2 = 0,5 кг, жёсткости пружин: k1 = 20 Н/м, k2 = 10 Н/м, радиус качения цилиндра составляет r = 0,2 м. Расстояние от точки крепления вертикальной пружины до оси цилиндра l = 0,22 м.

1. Рассматриваемая в задаче колебательная система имеет одну степень свободы, поэтому положение любой движущейся точки, принадлежащей системе, можно однозначно охарактеризовать одной обобщённой координатой, в качестве которой целесообразно взять линейное перемещение рейки с началом системы отсчёта в положении статического равновесия.

3. При перемещении рейки на расстояние х каток поворачивается на угол .

4. Запишем уравнение кинетической энергии колебательной системы

. (2)

5. Подставим в уравнение кинетической энергии значение момента инерции цилиндра и его угловой скорости

. (3)

. (4)

6. Из уравнения (4) определим приведённую массу (инерционный коэффициент)

. (2)

7. Коэффициент упругости системы определим путём анализа уравнения потенциальной энергии системы

. (3)

8. Коэффициент упругости системы, таким образом, равен

. (4)

9. Циклическая частота собственных колебаний системы

. (5)

10. Собственная частота колебаний

. (6)

3.2.5. Найти циклическую частоту собственных колебаний механической системы, состоящей из балки длиной 2l с грузом на конце массой m = 1 кг. Второй конец балки закреплён шарнирно, в своей средней части балка опирается на пружину жёсткости k =36 H/м.

1. В положении равновесия пружина под действием веса груза деформируется на величину lj0, т. е. на середину балки действует сила упругости

. (1)

2. Уравнение моментов относительно центра шарнирной опоры позволяет определить величину j0

. (2)

3. Предположим далее, что после сообщения грузу импульса угол отклонения балки составит j + j0, что обеспечит действие со стороны пружины силы

. (3)

4. Уравнение вращательного движения балки относительно шарнира будет иметь следующий вид

, (4)

, (5)

. (6)

5. Приведённая масса системы, таким образом, определяется как

. (7)

6. Циклическая частота собственных колебаний

. (8)

3.2.6. Модель крыла самолёта или рулей глубины подводной лодки или торпеды можно представить в виде жёсткой пластинки с шарнирным закреплением одного конца и подпружиненным вторым концом. Пластинка обтекается потоком газа или жидкости со скоростью v, направленной вдоль пластины. Определить критическое значение скорости, соответствующее потере устойчивости пластинкой, т. е. возникновению колебаний.

1. При отклонении пластинки от горизонтального положения статического равновесия, когда на неё действует сила тяжести и реакции опор, возникают силы, обусловленные гидродинамическими давлениями. Главный вектор этих сил, приложенных в сечении пластинки, отстоящем на расстоянии b от упругой опоры

(1)

где СХ, СY — постоянные коэффициенты, r — плотность жидкости или газа, j — угол отклонения пластинки, l — длина пластинки.

2. Момент сил относительно шарнирного закрепления

, (2)

. (3)

3. Дифференциальное уравнение движения

. (4)

4. Условие устойчивости

. (5)

3.2.7. Вычислить кинетическую энергию механической системы, состоящей из пружины массой m и прикрепленного к ней груза массой M, совершающего малые гармонические свободные колебания. Смещение точек пружины пропорционально их расстоянию до подвеса О.

1. Кинетическая энергия колебательной системы будет складываться из энергии возвратно-поступательного движения груза и кинетической энергии движущейся пружины

, (1)

где KМ — кинетическая энергия тела массой М, Km — кинетическая энергия пружины.

2. Если выбрать вертикальную ось oy, направленную вниз, то кинетическую энергию тела можно представить в традиционном виде

. (2)

3. Энергию пружины будем рассматривать, задавшись её длиной в статическом состоянии l и линейной плотностью r (кг/м). Выделим на длине пружины элемент её длины ds, который будет иметь смещения x одинаковые по всей длине пружины и совпадающие со смещениями груза. Это даёт основание записать следующее соотношение

. (3)

4. Кинетическая энергия элемента пружины длины dy определится на основании уравнения (3) следующим образом

. (4)

. (5)

5. Энергию всей пружины определится посредствам определённого интеграла взятого в пределах от 0 до l:

(6)

. (7)

6. Реализуем уравнение (1), используя значения полученных энергий груза и пружины

, (8)

величина, стоящая в скобках называется приведённой массой колебательной системы.

Таким образом, уравнение (8) при заданном законе движения груза позволяет определить величину кинетической энергии колебательной системы в любой момент времени, включая и амплитудные значения, которые будут иметь место при sin(wt+j0) = 1.

Видео:Математические и пружинные маятники. 11 класс.Скачать

Определение момента инерции физического маятника

ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ

Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О, не проходящей через центр масстела точку С (рис. 2.1).

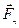
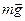
Если маятник выведен из положения равновесия на некоторый угол j, то составляющая силы тяжести уравновешивается силой реакции оси О, а составляющая стремится возвратить маятник в положение равновесия. Все силы приложены к центру масс тела. При этом

. (2.1)

Знак минус означает, что угловое смещение j и возвращающая сила имеют противоположные направления. При достаточно малых углах отклонения маятника из положения равновесия sinj » j, поэтому F_t » -mgj. Поскольку маятник в процессе колебаний совершает вращательное движение относительно оси О, то оно может быть описано основным законом динамики вращательного движения

, (2.2)

где М – момент силы F_t относительно оси О, I – момент инерции маятника относительно оси О, – угловое ускорение маятника.

Момент силы в данном случае равен

где l – расстояние между точкой подвеса и центром масс маятника.

С учетом (2.2) уравнение (2.3) можно записать

(2.4)

, (2.5)

где .

Решением дифференциального уравнения (2.5) является функция, позволяющая определить положение маятника в любой момент времени t,

Из выражения (2.6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с амплитудой колебаний j₀, циклической частотой , начальной фазой a₀ и периодом, определяемым по формуле

, (2.7)

где L=I/(mg) – приведенная длина физического маятника, т. е. длина такого математического маятника, период которого совпадает с периодом физического маятника. Формула (2.7) позволяет определить момент инерции твердого тела относительно любой оси, если измерен период колебаний этого тела относительно этой оси. Если физический маятник имеет правильную геометрическую форму и его масса равномерно распределена по всему объему, в формулу (2.7) можно подставить соответствующее выражение для момента инерции (Приложение 1).

В эксперименте исследуется физический маятник, называемый оборотным и представляющий собой тело, колеблющееся вокруг осей, расположенных на разном расстоянии от центра тяжести тела.

Оборотный маятник состоит из металлического стержня, на котором неподвижно укреплены опорные призмы О₁ и О₂ и две подвижные чечевицы А и B, которые могут закрепляться в определённом положении с помощью винтов (рис. 2.2).

Физический маятник совершает гармонические колебания при малых углах отклонения от положения равновесия . Период таких колебаний определяется соотношением (2.7)

,

где I – момент инерции маятника относительно оси вращения, m – масса маятника, d – расстояние от точки подвеса до центра масс, g – ускорение силы тяжести.

Применяемый в работе физический маятник имеет две опорные призмы О₁ и О₂ для подвешивания. Такой маятник называется оборотным.

Сначала маятник подвешивают на кронштейн опорной призмой О₁ и определяют период колебаний Т₁ относительно этой оси:

(2.8)

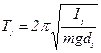
Затем маятник подвешивают призмой О₂ и определяют Т₂:

. (2.9)

Таким образом, моменты инерции I₁ и I₂ относительно осей, проходящих через опорные призмы О₁ и О₂, будут соответственно равны и . Масса маятника m и периоды колебаний Т₁ и Т₂ могут быть измерены с высокой степенью точности.

По теореме Штейнера

, (2.10)

, (2.11)

где I₀ – момент инерции маятника относительно оси, проходящей через центр тяжести. Таким образом, момент инерции I₀ можно определить,зная моменты инерции I₁ и I₂.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Снимите маятник с кронштейна, поместите его на трёхгранную призму так, чтобы расстояния от опоры до призм О₁ и О₂ не были равны между собой. Передвигая чечевицу вдоль стержня, установите маятник в положение равновесия, после чего закрепите чечевицу винтом.

2. Измерьте расстояние d₁ от точки равновесия (центр масс С) до призмы О₁ и d₂ – от С до призмы О₂.

3. Подвесив маятник опорной призмой О₁ , определите период колебаний 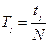, где N – число колебаний (не более 50).

4. Аналогичным образом определите период колебаний Т₂ относительно оси, проходящей через ребро призмы О₂ .

5. Подсчитайте моменты инерции I₁ и I₂ относительно осей, проходящих через опорные призмы О₁ и О₂, по формулам и , измерив массу маятника m и периоды колебаний Т₁ и Т₂. Из формул (2.10) и (2.11) определите момент инерции маятника относительно оси, проходящей через центр тяжести (масс) I₀. Из двух опытов найдите среднее .

6. Передвинув чечевицу А и найдя новое положение центра тяжести С, повторите опыт. Результаты измерений и вычислений занесите в таблицу (см. образец, табл.1).

Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ОДНОРОДНОГО ДИСКА МЕТОДОМ КОЛЕБАНИЙ. ФИЗИЧЕСКИЙ МАЯТНИК

1 Федеральное агентство по образованию Томский государственный архитектурно-строительный университет Институт заочного и дистанционного обучения ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ОДНОРОДНОГО ДИСКА МЕТОДОМ КОЛЕБАНИЙ. ФИЗИЧЕСКИЙ МАЯТНИК Методические указания Составители Н. О. Солоницина, Л. И. Тришкина, А. А. Клопотов Томск 006

2 Определение момента инерции однородного диска методом колебаний. Физический маятник: методические указания / Сост. Н.О. Солоницина, Л.И. Тришкина, А.А. Клопотов. Томск : Изд-во Томского государственного архитектурно-строительного университета, с. Рецензент доцент В. Б. Каширин Редактор Т.С. Володина Методические указания к лабораторным занятиям по теме «Механика» для студентов дневной и заочной форм обучения всех специальностей, кроме специальности «Архитектура». Печатается по решению методического семинара кафедры физики 3 от г. Утверждены и введены в действие проректором по учебной работе В.С. Плевковым с до Изд. лиц от Подписано в печать г. Формат 60 84/16. Бумага офсет. Гарнитура Таймс. Печать офсет. Уч.-изд.л. Тираж 500 экз. Заказ Изд-во ТГАСУ, , г. Томск, пл. Соляная, Отпечатано с оригинал-макета в ООП ТГАСУ , г. Томск, ул. Партизанская, 15

3 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ОДНОРОДНОГО ДИСКА МЕТОДОМ КОЛЕБАНИЙ. ФИЗИЧЕСКИЙ МАЯТНИК 1. Цель работы Цель работы: определение момента инерции однородного диска относительно оси вращения, проходящей через центр тяжести диска, перпендикулярно к его плоскости.. Теоретическая часть Рассмотрим абсолютно твердое тело, имеющее ось вращения О 1 О (рис. 1). Абсолютно твердым телом называют тело, у которого остается неизменным расстояние между любыми двумя произвольно выбранными точками при его поступательном и вращательных движениях и при воздействии на это тело внешних сил. Мысленно расчленим это тело на совокупность n материальных точек. Каждая материальная точка обладает некоторой массой m i (i = 1,,3 n) и находится на соответствующем расстоянии r i от оси вращения. Тогда величину I m i r i = i Рис. 1 называют моментом инерции точки. Под моментом инерции тела относительно оси вращения понимают величину I, численно равную пределу: n lim m i r i (или: I = r dm, где интегри- n i= 1 3

4 рование ведется по всему объему тела). Если плотность тела ρ постоянна (однородное тело), то 4 dm = ρdv и I = ρ r dm. Очевидно, что момент инерции данного тела зависит от распределения масс отдельных точек тела по отношению к оси вращения. В случае, если ось вращения твердого тела горизонтальна и не проходит через центр масс (тяжести) тела, то тело, будучи выведено из состояния устойчивого равновесия, начнет совершать под действием силы тяжести колебания относительно этой оси. Напомним, что колебаниями называются процессы, отличающиеся Рис. той или иной степенью повторяемости. Иными словами, мы будем иметь дело с физическим маятником. Физическим маятником называется абсолютно твердое тело, способное совершать колебания под действием силы тяжести вокруг неподвижной точки О, не совпадающей с центром масс С (рис. ). Найдем выражение для периода колебаний физического маятника. Для этого рассмотрим колебания некоторого тела, обладающего массой m, ось вращения которого О 1 О горизонтальна и проходит через точку О, находящуюся на расстоянии l от центра тяжести тела С (рис. ). Момент силы тяжести, действующей на тело относительно оси О 1 О, имеет величину M = mgl sin φ, и уравнение ( v)

5 динамики вращательного движения тела примет в данном случае вид: d ϕ I = mgl sin ϕ, (1) dt d ϕ где величина углово- dt го ускорения. Знак минус в равенстве (1) обусловлен тем, что вектор момента сил тяжести и вектор поворота направлены по оси вращения, но в противоположные стороны (рис. 3). Если углы поворота тела относительно положения равновесия малы, то можно считать, что sin φ φ и уравнение (1) имеет вид: d ϕ mgl = ϕ = 0 dt I. () Рис. 3 Уравнение () описывает колебательное движение тела относительно оси О 1 О и представляет собой дифференциальное уравнение. Решение уравнения имеет вид: φ = φ 0 sin (ωt + α), (3) где φ 0 максимальный угол отклонения от положения равновесия, который является амплитудой в уравнении; (ωt + α) фаза колебания; α начальная фаза колебания; ω циклическая частота колебаний, которая связана с периодом колебаний физического маятника Т следующим соотношением π ω =. В нашем T 5

6 mgl случае ω =. Тогда период колебаний физического маятника равен: I I T = π (4) mgl Таким образом, по формуле (4) можно найти период колебаний для любого физического маятника, при условии малых углов поворота маятника относительно положения равновесия. Колебания, которые совершает физический маятник, относятся к простейшим типам колебаний так называемым гармоническим колебаниям, при которых движение тела описывается по синусоидальному (или косинусоидальному) закону в зависимости от времени. Другим примером простого гармонического движения могут служить колебания, совершаемые математическим маятником. Под математическим маятником понимают маятник, состоящий из точечной массы, подвешенный на невесомой и нерастяжимой нити. Почти каждый колебательный процесс можно считать простым гармоническим движением при достаточно малой амплитуде. Рассмотрим физический маятник, состоящий из однородного диска, горизонтальная ось вращения которого проходит через центр тяжести и к ободу которого прикреплен шарик. 6

7 Рис. 4 Если масса диска М, масса шарика m, момент инерции диска относительно данной оси I д, а момент инерции диска относительно этой же оси I ш, то для периода колебаний этого маятника на основании (4) имеем: I д + I ш T = π, (5) (M + m) lg где I д + I ш = I момент инерции данного физического маятника. Поскольку проводить измерения расстояния от оси вращения маятника до центра тяжести (С) затруднительно, поэтому исключим величину l из формулы (5). Для этого воспользуемся условием равновесия тела относительно оси, проходящей через центр масс тела (правило моментов) (рис. 4). Условие равновесия нашей системы относительно оси, проходящей через центр тяжести системы (С), имеет вид: 7

8 Mgl = (х + r)mg, где отрезок х = R — l и R радиус диска (рис. 4); r радиус маленького шарика; l расстояние от центра диска до центра тяжести диска с шариком; m масса шарика; М масса диска. Подставляя в условие равновесия значения х, получим: Мl = (R — l + r) m. Решим это уравнение относительно l и получим выражение: (R + r)m l =. M + m Подставим это значение в (4) и запишем период колебаний физического маятника в виде: I д + I ш T = π. (6) (R + r)mg Теперь возведем обе части уравнения (6) в квадрат и выразим момент инерции диска I д : Рис. 5 8

9 T I д = (R + r)mg I ш. (7) 4π Для вычисления момента инерции шарика применим теорему Щтейнера: момент инерции I относительно произвольной оси равен моменту инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела, сложенной с произведением массы тела m на квадрат расстояния а между осями: I = I 0 + m а. Тогда, согласно теореме Штейнера, для нашего случая момент инерции шарика I ш относительно оси вращения диска О 1 О запишем в виде (рис. 5): I ш = I 0 + m(r+r), (8) где I 0 момент инерции шара относительно оси, проходящей через центр тяжести шара: I 0 = 5 mr, получим из выражения для момента инерции диска в виде: T I д = (R + r)mg mr m(r + r). (9) 4π 5 3. Ход работы В данной лабораторной работе на экране компьютера моделируются колебания однородного диска с подвешенным шариком. По результатам эксперимента нужно вычислить его момент инерции. Для выполнения задания виртуальной физической лабораторной работы необходимо запустить программу, щелкнув левой клавишей мышки по ярлыку на экране «Физ. Лаб.». После этого на экране появится окно, в котором будет присутствовать список лабораторных работ. 9

10 Установить курсор на работе «Определение момента инерции однородного диска методом колебаний» и мышкой активизировать работу программы. В результате будет открыто окно, в котором будет присутствовать таблица с командами: О программе О работе Эксперимент Последовательно вызывая пункты меню в таблице, необходимо предварительно ознакомиться с лабораторной работой и порядком ее выполнения. После обращения к команде «Эксперимент» на экране появляется окно с кнопками, управляющими колебаниями маятника, секундомером, линейкой и самим маятником (рис. 6). Для выполнения работы необходимо выполнить следующие действия. 1. Измерить диаметр диска и шарика при помощи линейки. Линейка может перемещаться при помощи мыши при нажатой левой кнопке.. Запустить колебания. Колебания осуществляются после нажатия на кнопку «Пуск» управления колебаниями. Кнопка «Сброс» возвращает маятник в первоначальное положение. 10

11 Рис Измерить время 0 полных колебаний. При помощи кнопки «Пуск» включить секундомер и измерить время 0 полных колебаний. Для включения секундомера нажать «Стоп». Опыт повторить 10 раз. 4. Вычислить среднее время и средний период 0 колебаний. Определить средний период колебаний по формуле T = t n, где t среднее время колебаний, n число колебаний. 5. По полученным экспериментальным данным по формуле (7) вычислить момент инерции диска. При этом необходимо перевести все физические величины в одну систему единиц в систему СИ. В расчетах принять массу шарика равной 00 грамм. 6. Рассчитать погрешность окончательного результата. Для расчета погрешности окончательного результата необходимо использовать формулы, приведенные ниже в приложении к лабо- 9 11

12 раторной работе. 4. Обработка результатов измерений Анализ результатов измерений показывает, что случайные и систематические погрешности проявляют себя лишь при измерении времени n колебаний диска и имеют один и тот же порядок величины. Максимальная погрешность вычисляется по формуле: д I I д I д I д = T + m + d д, (10) Т m d I д mg(d д + d ш )Т где = ; Т 4π I д T = (d д + d ш )g 0,1d ш 0,5(d д + d ш ) ; m 8π I д T mg = 0,5m(d д + d ш ). d д 8π Окончательный результат расчетов записывают в виде: I = I ± I д ср. д В работе абсолютная погрешность округляется до одной значащей цифры. д 1 КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Сформулировать цель работы.. Какое тело называют абсолютно твердым? 3. Какой маятник называют физическим? Записать формулу периода физического маятника. 4. Какой маятник называют математическим?

13 5. Что называется моментом инерции материальной точки тела, моментом инерции твердого тела? 6. Что такое колебание и какие колебания называют гармоническими? 7. Дайте определение амплитуды, периода, частоты и фазы колебаний. 8. Как связаны между собой период и частота колебаний? 9. От чего зависит момент инерции тела? 10. Сформулируйте теорему Штейнера. 11. Что характеризуют величины Т, m, d Д и как их можно определить? Схема записи результатов измерений Все результаты измерений заносятся в таблицы: число колебаний диска n Время колебаний t, с Период колебаний Т T = t/n, с Среднее значение периода Тср. Тср. = T/N, с Диаметр диска d д, см 1 5 Средний диаметр диска d д ср., см Диаметр шарика d ш, см Средний диаметр шарика d ш ср., см Масса шарика m, г 13

14 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ 1. Трофимова, Т.В. Курс физики / Т.В. Трофимова. М. : Высшая школа, с.. Сивухин, Я. В. Общий курс физики. Т.1. / Я.В. Сивухин. М. : Наука, главная редакция Ф-МЛ, с. 14

💡 Видео

Урок 94. Вычисление моментов инерции телСкачать

Урок 92 (осн). Колебательное движение. МаятникиСкачать

Почти всё о маятникеСкачать

Физический маятникСкачать

Физический маятникСкачать

Лабораторная работа №2 - "Физический маятник"Скачать

Лабораторная работа - 8М: Определение момента инерции маятника Максвелла.Скачать

Крутильные колебания.Скачать

#21 Измерение момента инерции маятника ОбербекаСкачать

Колебания математического и пружинного маятников. 9 класс.Скачать