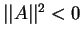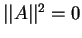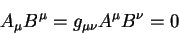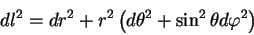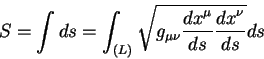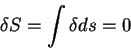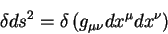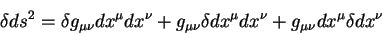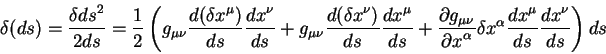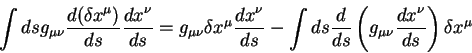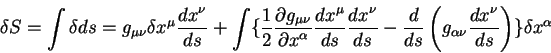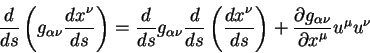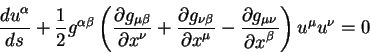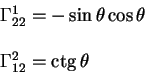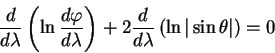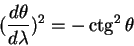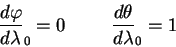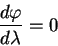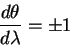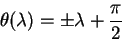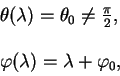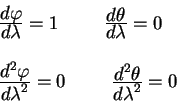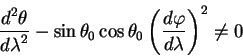- Формула Клеро
- Уравнение клеро для геодезической линии
- 5. Неэвклидова геометрия
- 5.1 Метрика искривленного пространства — времени
- 5.1.1 Примеры метрики искривленного пространства
- 5.2 Геодезические линии в неэвклидовой геометрии
- 5.2.1 Геодезические линии на поверхности сферы
- Движение по экватору
- Движение по меридиану
- Движение по малому кругу
- Теорема Клеро. Формулы определения нормальной силы
- 🔥 Видео
Видео:Решение уравнения КлероСкачать

Формула Клеро
- Когда геодезическая плоскости вращения проходит через точку M этой прямой, а I представляет собой угол, пересекающий меридиан, который проходит через r и проходит расстояние от точки A. Отношение к оси и ко всем точкам линии г Синс=. 1 Фактически, если мы примем во внимание точки, представляющие геодезические при предыдущих условиях, то момент импульса, или скорость точки относительно оси, которая вызывается одновременно, становится постоянной. Так как угловой момент для оси Oz равен r2, то постоянная величина этого момента точно равна постоянной C области на плоскости, перпендикулярной оси.
Если, наоборот, дан только частный закон движения, не содержащий произвольных постоянных, или содержащий только одну произвольную постоянную, то задача будет неопределенной. Людмила Фирмаль
Разложим скорость v движущейся точки M на 2 составляющие.1 vsin контактирует с параллельной линией, проходящей через точку M, а другая vcosi контактирует с меридианом. Момент скорости относительно оси вращения равен сумме моментов этих 2 составляющих, но 2 й момент равен нулю, поэтому момент скорости равен моменту рысини 1 го component. So … РВ грех я = с Но поскольку v = v0, это дает вам Формулу 1.
- Важна постоянная k, следовательно, во Входит в уравнение геодезическое пункт 273. Примечание соотношения 1 не характеризуют геодезические объекты. Если линия удовлетворяет этому уравнению, то она является либо геодезической, либо параллельной line.
Но, как заметил Бертран, формула Лагранжа не дает всех законов для силы, при которых движение будет таутохронным. Людмила Фирмаль
Дело в том, что уравнение 1 явно заполнено R = k, i = so параллельно. Решением является специальный Интеграл r = k уравнения G , dr = 0. Этому числу приписывают знак или — в зависимости от того, наступает ли рассматриваемый момент после или до начального момента. траектория — прямая линия. точки в функции времени. Изменение этой скорости пропорционально изменению времени. Говорят, что определяемое таким образом прямолинейное движение является равнопеременным. есть полярный вектор, приложенный к движущейся точке.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Решение уравнения ЛагранжаСкачать

Уравнение клеро для геодезической линии
Видео:Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

5. Неэвклидова геометрия
В произвольной геометрии рассматриваются произвольные преобразования координат:
как видно из приведенных преобразований, они описывают просто переход от сферических к декартовым координатам.
Дифференциал в нетильдованной системе связан с дифференциалом в системе координат с тильдой уравнениями вида:
В геометрии вводится понятие геометрического объекта. Не перечисляя всех объектов геометрии назовем только скаляры, векторы и тензоры. Строго говоря, все перечисленные величины являются тензорами, так скаляр является тензором нулевого ранга, а вектор тензором первого ранга. Однако исторически принято выделять скаляры и векторы.
Скалярная величина (или скаляр) при преобразованиях системы координат не преобразуется,
Вектором называется величина, которая содержит четыре компоненты, преобразуемые согласно правилу:
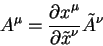 | (5.1) |
для контравариантных компонент и
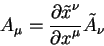 | (5.2) |
для ковариантных компонент.
Как можно заметить, из закона преобразования (5.1) преобразование контравариантных компонент какого — либо вектора подобно преобразованию дифференциалов координат, представляющих разность положений двух точек. Следовательно контравариантные компоненты вектора можно представить как систему из двух точек, с указанием какая из точек является первой, а какая является второй. Примером контравариантных компонент является четырехмерная скорость какого — либо тела.
Примером ковариантных компонет вектора является градиент некоторого поля:
Образом градиента от поля являются наборы двумерных поверхностей определяющих постоянство поля 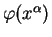
Выпишем также правило по которому преобразуются компоненты тензора второго ранга:
Геометрическая величина 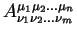
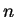
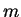
называется тензором ранга 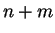
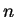
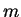
В алгебре тензоров определяется суммирование тензоров одинакового ранга и с одинаково расположенными индексами:
умножение определено для тензоров любого ранга с произвольно расположенными индексами:
В тензорной алгебре определяют также свертку двух тензоров по правилу:
для произвольного расположения индексов важно только, чтобы индекс по которому проводится свертка в первом тензоре был верхним, во втором — нижним (или наоборот, в первом — нижним, а во втором -верхним). Положение и количество остальных индексов переносится в свертку по их месту. Свертки могут быть образованы различными способами, однако каждое суммирование должно выполняться по верхнему и нижнему индексу. Например, сумма
не является тензором, как легко убедиться рассмотрев закон преобразования этой величины.
В современной тензорной алгебре, анализе и физике пользуются правилом суммирования Эйнштейна, который для удобства ввел следущее обозначение:
при этом индекс 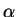
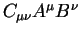
Повсюду в этой книге мы будем использовать это правило, два повторяющихся индекса один верхний, другой — нижний будет означать, что по ним производится суммирование.
Определим также обратные тензоры согласно уравнению:
Здесь 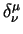
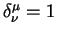
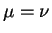
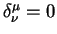
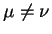
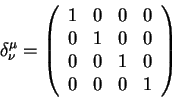 | (5.3) |
Свертка двух тензоров понижает ранг произведения. Так, важный пример показывает, что произведение ковариантных компонент вектора на контравариантные компоненты является инвариантом:
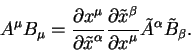 | (5.4) |
Различные авторы [8], [9], [12] вводят также операцию симметрирования, албтернирования, выключения индексов и т.п. Для нас важной остается только последняя операция над тензорами — образование следа, образование поперечной части тензора и образование поперечно — бесследовой части тензора, которые будут применяться во второй части книги. Однако для их определения нам придется использовать метрику, поэтому отложим введения этих понятий после обсуждения метрики.
Видео:Дифференциальные уравнения не разрешенные относительно производной | poporyadku.schoolСкачать

5.1 Метрика искривленного пространства — времени
Геометрия четырехмерного пространства — времени полностью определяется десятью функциями, которые являются компонентами симметричного тензора второго ранга. Метрика четырехмерного интервала есть:
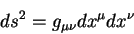 | (5.5) |
Здесь 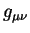
Компоненты метрического тензора являются, вообще говоря, функциями всех четырех координат.
Преобразованием координат всегда можно добиться того, чтобы компоненты метрического тензора были приведены к виду метрики Минковского:
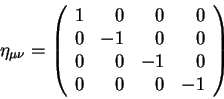 | (5.6) |
В пространстве с заданной метрикой можно определить связь между ковариантными и контравариантными компонентами тензоров, так для вектора связь между этими компонентами задается уравнениями:
Теперь можно определить норму вектора, аналогично тому, как это делается в эвклидовой геометрии. Норомой вектора по определению полагают величину [8], [9], [12]:
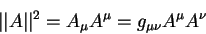 | (5.7) |
В зависимости от того, чему равна норма ветора его называют:
- времениподобным, если
0$» width=»82″ height=»38″ >
- пространственноподобным, если
- изотропным, если
Норма называется также длиной вектора. Как видно из определения изотропного вектора он обладает нулевой длиной.
Рассмотрим свертку двух векторов. Два вектора, которые удовлетворяют условию:
называются ортогональными. Отсюда можно сделать вывод, что изотропный вектор ортогонален самому себе и любому другому изотропному вектору. Следует заметить, что таким свойством обладают только изотропные вектора.
Кроме этого важного свойства приведем также уравнение описывающее угол 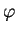
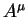
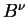
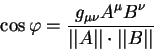 | (5.8) |
Здесь следует заметить, что оба вектора 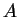
Видео:14. Уравнения Лагранжа и КлероСкачать

5.1.1 Примеры метрики искривленного пространства
Приведем примеры метрики искривленного пространства. На самом деле в быту мы сталкиваемся с примера геометрии искривленного пространства значительно чаще, чем привыкли думать. Поверхность мяча, поверхность спинки кресла, поверхность кувшина или графина — вот неполный список двумерных искривленных пространств. Примеры идеальных плоскостей, таких как крышка стола или ровный листок бумаги в этом ряду выглядят, скорее исключениями, чем правилом.
Приведем в качестве примера метрику на поверхности сферы. Для этого выпишем вначале метрику эвклидова пространства в сферической системе координат:
Будем считать, что мы вычисляем расстояние только между теми точками, которые лежат на поверхности сферы радиуса 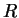
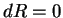
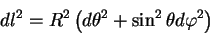 | (5.9) |
теперь метрика описывает поверхность сферы, а геометрия, которую описывает данный метрический тензор является неэвклидовой.
Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

5.2 Геодезические линии в неэвклидовой геометрии
В эвклидовой геометрии очень важным понятием является прямая между двумя точками, которая к тому же является кратчайшим расстоянием между этими точками. В неэвклидовой геометрии понятие прямой заменяется понятием геодезической линии, которая является экстремальным путем между двумя точками.
Для нахождения уравнения геодезической линиии применим вариационное исчисление.
Длина линии в геометрии общей теории относительности есть интеграл по интервалу между двумя событиями разделенными по времени и пространству:
Линии экстремального пути удовлетворяет условию:
Здесь символ 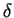
Для вычисления вариации величины 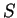
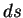
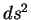
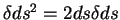
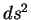
правую часть этого равенства можно представить в виде суммы:
Воспользуемся равенствами 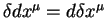
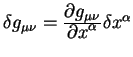
Третий член в круглых скобках уже приведен к виду пригодному для вычисления первой вариации. Для приведения к такому же виду первых двух членов воспользуемся равенством:
Воспользуемся теперь этими равенствами и вычислим первую вариацию полного пути:
В этом уравнении первый член после второго знака равенства представляет из себя вариации в конечных точках пути, по определению эти вариации равны нулю [13], [14]. Член под знаком интеграла в фигурных скобках должен обращаться в нуль на геодезической линии. Это и дает нам уравнение геодезической линии:
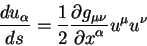 | (5.10) |
Здесь 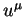
Уравнение, которое мы получили является уравнением второго порядка. В случае эвклидовой геометрии, когда все компоненты метрического тензора являются диагональными и равны единице, правая часть равенства (5.10) равна нулю. Тогда решение этого уравнения есть 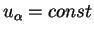
Приведем это уравнение к стандартной форме, принятой в неэвклидовой геометрии. Для этого воспользуемся тождеством:
Подставив его в левую часть уравнения (5.10) получаем уравнение вида:
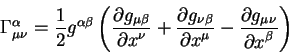 | (5.11) |
называется символом Кристоффеля. Символ Кристоффеля имеет три индекса и не является тензором. В алгебре такие величины носят название символы первого рода.
Стандартный вид уравнения геодезической линии в неэвклидовой геометрии записывается с помощью символа Кристоффеля:
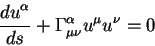 | (5.12) |
Кроме этого, стандартного вида уравнения геодезической линии, можно также записать как меняется дифференциал касательного вектора 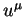
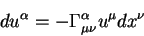 | (5.13) |
Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

5.2.1 Геодезические линии на поверхности сферы
Рассмотрим в качестве примера геодезические линии на сфере — двумерной неэвклидовой поверхности. Метрический тензор на поверхности сферы имеет вид:
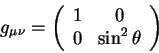 | (5.14) |
Контравариантные компоненты метрического тензора на поверхности сферы есть:
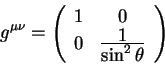 | (5.15) |
Вычисляя символ Кристоффеля получаем, что все компоненты равны нулю за исключением двух:
Уравнения геодезических линий имеют вид:
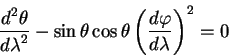 | (5.16) |
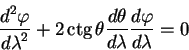 | (5.17) |
Здесь 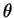
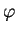
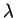
При приведении к первому интегралу уравнение (5.17) получает вид:
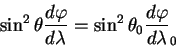 | (5.18) |
Здесь 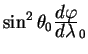
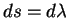
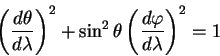 | (5.19) |
Рассмотрим два частных случая геодезических линий.
Движение по экватору
Пусть наша линия начинается на экваторе 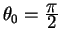
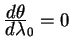
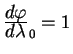
Решение для геодезической линии получается из уравнений (5.18, 5.19). Действительно, правая часть равенства (5.18) есть 1. Подставляем выражение для 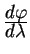
Удовлетворяет этому уравнению только значения 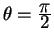
Движение по меридиану
Рассмотрим теперь движение вдоль меридиана и покажем, что меридиан также является геодезической линией. Теперь вектор, касательный к линии имеет компоненты:
Начальную точку также выберем на экваторе 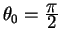
откуда следует, что 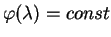
откуда непосредственно следует, что
Не рассматривая общего случая решения системы (5.18, 5.19) упомянем только, что экватор и меридиан на поверхности сферы являются частными случаями большого круга — сечения поверхности сферы плоскостью, которая проходит через центр сферы. Рассматривая трехмерные вращения, можно показать, что только отрезок большого круга на сфере представляет кусок геодезической линии. Полная геодезическая линия представляет из себя большой круг.
Движение по малому кругу
Продемонстрируем отличие произвольной линии от геодезической линии на примере малого круга на сфере. Малый круг на сфере — это сечение сферы плоскостью, которая не проходит через центр сферы.
Выберем малый круг так, чтобы он был сечением с 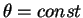
отсюда легко найти первые и вторые производные от координат по афинному параметру:
Подставляя эти значения в уравнения геодезических приходим к противоречию:
Таким образом малый круг на сфере не является геодезической линией.
Видео:Дынников И. А. - Классическая дифференциальная геометрия - Теорема КлероСкачать

Теорема Клеро. Формулы определения нормальной силы
Тяжести
Клеро дал вывод своей теоремы (1743), основываясь на исследованиях фигур равновесия тел с неоднородной массой. При этом он принял Землю по форме за эллипсоид вращения с малым полярным сжатием, состоящий внутри из эллипсоидальных, однородных по плотности слоев, имеющих общий центр и совпадающие главные оси инерции.
Теорема Клеро позволяет определить нормальную силы тяжести на поверхности земного эллипсоида и сжатие земного эллипсоида. Она состоит из двух формул.
Первая формула теоремы Клеро устанавливает закон изменения нормальной силы тяжести на поверхности земного эллипсоида. Эта формула с учетом величин порядка второй степени сжатия имеет вид:







где 




Вторая формула теоремы Клеро с членами второго порядка записывается в виде:

где 
Из 2.39 может быть вычислено сжатие 


Вторая формула теоремы Клеро позволяет определить сжатие 
В практике гравиметрических и геодезических работ широко используется первая формула теоремы Клеро, для которой определены численные значения коэффициентов 


В странах бывшего СССР используется формула Гельмерта (1901—1908 гг.), которая, по сути, как и другие приведенные ниже формулы, является первой формулой теоремы Клеро с численными значениями коэффициентов.
Формула Гельмерта записывается в виде:


Данную формулу применяют в странах бывшего СССР вплоть до настоящего времени. Она была выведена Гельмертом на основании результатов измерения силы тяжести на 1603 пунктах. Значение сжатия Земли, соответствующее формуле Гельмерта, то есть вычисленное по формуле (3.10) при 

В некоторых странах используется формула нормальной силы тяжести Кассиниса, рекомендованная в качестве «международной формулы» в 1930 г. на съезде Международного геодезического союза в Стокгольме.
Формула Кассиниса имеет вид:

Эта формула соответствует эллипсоиду Хейфорда со сжатием 
Международная формула для геодезической референц-системы 1967 года, рекомендованная на ХV Генеральной ассамблее Международного геодезического и геофизического союза в Москве (1971 г.), имеет следующие коэффициенты:

Следует отметить, что коэффициент 
И, наконец, в 1984 году Мориц опубликовал международную формулу для геодезической референц-системы 1980 года со следующими коэффициентами:

Коэффициенты в двух последних формулах получены с использованием спутниковых данных и с учетом массы атмосферы. Сжатия эллипсоидов для них составляют, соответственно, 1:298.247 и 1:298.257.
Переход той или иной страны к новой формуле нормальной силы тяжести связан с перевычислением большого числа гравиметрических данных, с изменением гравиметрических карт и каталогов. Поэтому, учитывая чисто служебный характер нормальной формулы, не следует прибегать к частому изменению ее коэффициентов. В случае необходимости проще вводить поправки в конечные выводы.
🔥 Видео
9 класс, 6 урок, Уравнение окружностиСкачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

11. Уравнения в полных дифференциалахСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Дифференциальные уравнения. 11 класс.Скачать

Математика без Ху!ни. Уравнение касательной.Скачать

Прямая геодезическая задача. Формулировка. ОпределениеСкачать

Попеленский Ф. Ю. - Дифференциальная геометрия и топология. Семинары - Семинар 12Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать




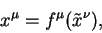
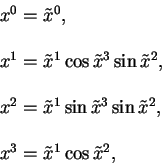
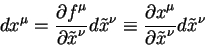
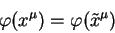
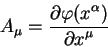
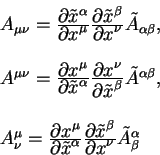
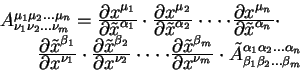
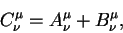
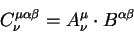
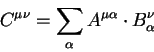
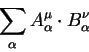
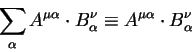
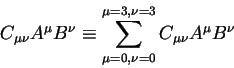
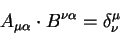
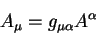
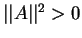 0$» width=»82″ height=»38″ >
0$» width=»82″ height=»38″ >